二叉树
平衡二叉树
它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
完全二叉树
对一颗具有n个结点的二叉树按层进行编号,如果编号为i (1 <= i <= n)的结点与同样深度的满二叉树节点编号为i的结点在二叉树中的位置完全相同,则这颗树,我们称之为完全二叉树。
满二叉树一定是完全二叉树,完全二叉树不一定是满二叉树。
哈夫曼树(Huffman Tree),又叫优二叉树,指的是对于一组具有确定权值的叶子结点的具有小带权路径长度(所有叶子结点路径长度的加权和)的二叉树。
顺序存储
完全二叉树顺序编号的所有左孩子都是偶数(2i),所有右孩子都是奇数(2i+1)
链式存储
定义存储结构
typedef char DataType;
typedef struct bnode
{
DataType data;
struct bnode *left;
struct bnode *right;
} bitree;
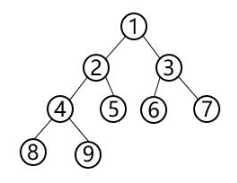
先序遍历(左-中-右):1,2,4,8,9,5,3,6,7
中序遍历(中-左-右):8,4,9,2,5,1,6,3,7
后序遍历(左-右-中):8,9,4,5,2,6,7,3,1
层次遍历(宽度优先遍历):利用队列,依次将根,左子树,右子树存入队列,按照队列的先进先出规则来实现层次遍历。1,2,3,4,5,6,7,8,9
深度优先遍历:利用栈,先将根入栈,再将根出栈,并将根的右子树,左子树存入栈,按照栈的先进后出规则来实现深度优先遍历。1,2,4,8,9,5,3,6,7
class Node:
def __init__(self,value=None,left=None,right=None):
self.value=value
self.left=left #左子树
self.right=right #右子树
def preTraverse(root):
'''
前序遍历
'''
if root==None:
return
print(root.value)
preTraverse(root.left)
preTraverse(root.right)
def midTraverse(root):
'''
中序遍历
'''
if root==None:
return
midTraverse(root.left)
print(root.value)
midTraverse(root.right)
def afterTraverse(root):
'''
后序遍历
'''
if root==None:
return
afterTraverse(root.left)
afterTraverse(root.right)
print(root.value)
if __name__=='__main__':
root=Node('D',Node('B',Node('A'),Node('C')),Node('E',right=Node('G',Node('F'))))
print('前序遍历:')
preTraverse(root)
print('\n')
print('中序遍历:')
midTraverse(root)
print('\n')
print('后序遍历:')
afterTraverse(root)
print('\n')
广度优先(队列,先进先出)
def BFS(self, root):
'''广度优先'''
if root == None:
return
# queue队列,保存节点
queue = []
# res保存节点值,作为结果
#vals = []
queue.append(root)
while queue:
# 拿出队首节点
currentNode = queue.pop(0)
#vals.append(currentNode.val)
print(currentNode.val, end=' ')
if currentNode.left:
queue.append(currentNode.left)
if currentNode.right:
queue.append(currentNode.right)
#return vals
深度优先(栈,后进先出)
def DFS(self, root):
'''深度优先'''
if root == None:
return
# 栈用来保存未访问节点
stack = []
# vals保存节点值,作为结果
#vals = []
stack.append(root)
while stack:
# 拿出栈顶节点
currentNode = stack.pop()
#vals.append(currentNode.val)
print(currentNode.val, end=' ')
if currentNode.right:
stack.append(currentNode.right)
if currentNode.left:
stack.append(currentNode.left)
#return vals


 浙公网安备 33010602011771号
浙公网安备 33010602011771号