面试
正则化之所以能够降低过拟合的原因在于,正则化是结构风险最小化的一种策略实现。
给loss function加上正则化项,能使得新得到的优化目标函数h = f+normal,需要在f和normal中做一个权衡(trade-off),如果还像原来只优化f的情况下,那可能得到一组解比较复杂,使得正则项normal比较大,那么h就不是最优的,因此可以看出加正则项能让解更加简单,符合奥卡姆剃刀理论,同时也比较符合在偏差和方差(方差表示模型的复杂度)分析中,通过降低模型复杂度,得到更小的泛化误差,降低过拟合程度。
L1正则化和L2正则化:
L1正则化就是在loss function后边所加正则项为L1范数,加上L1范数容易得到稀疏解(0比较多)。L2正则化就是loss function后边所加正则项为L2范数的平方,加上L2正则相比于L1正则来说,得到的解比较平滑(不是稀疏),但是同样能够保证解中接近于0(但不是等于0,所以相对平滑)的维度比较多,降低模型的复杂度。
机器学习中的Bias(偏差),Error(误差),和Variance(方差)有什么区别和联系?
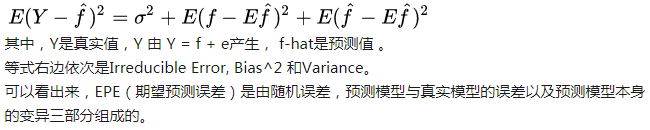
准: 偏差(bias)描述的是“用所有可能的训练数据集训练出的所有模型的输出的平均值” 与 “真实模型”的输出值之间的差异,简单讲,就是在样本上拟合的好不好。要想在bias上表现好,low bias,就得复杂化模型,增加模型的参数,但这样容易过拟合 (overfitting),过拟合对应上图是high variance,点很分散。low bias对应就是点都打在靶心附近,所以瞄的是准的,但手不一定稳。
确:方差(varience)描述的是不同的训练数据集训练出的模型”的输出值之间的差异,要想在variance上表现好,low varience,就要简化模型,减少模型的参数,但这样容易欠拟合(unfitting),欠拟合对应上图是high bias,点偏离中心。low variance对应就是点都打的很集中,但不一定是靶心附近,手很稳,但是瞄的不准。
误差(error)可以理解为loss,及学习的目标
这个靶子上的点(hits)可以理解成一个一个的拟合模型,如果许多个拟合模型都聚集在一堆,位置比较偏,如图中 high bias low variance 这种情景,意味着无论什么样子的数据灌进来,拟合的模型都差不多,这个模型过于简陋了,参数太少了,复杂度太低了,这就是欠拟合;但如果是图中 low bias high variance 这种情景,你看,所有拟合模型都围绕中间那个 correct target 均匀分布,但又不够集中,很散,这就意味着,灌进来的数据一有风吹草动,拟合模型就跟着剧烈变化,这说明这个拟合模型过于复杂了,不具有普适性,就是过拟合。
所以bias和variance的选择是一个tradeoff,过高的variance对应的概念,有点『剑走偏锋』『矫枉过正』的意思,如果说一个人variance比较高,可以理解为,这个人性格比较极端偏执,眼光比较狭窄,没有大局观。而过高的bias对应的概念,有点像『面面俱到』『大巧若拙』的意思,如果说一个人bias比较高,可以理解为,这个人是个好好先生,谁都不得罪,圆滑世故,说话的时候,什么都说了,但又好像什么都没说,眼光比较长远,有大局观。(感觉好分裂 )
K折交叉验证,当K值大的时候, 我们会有更少的Bias(偏差), 更多的Variance。当K值小的时候, 我们会有更多的Bias(偏差), 更少的Variance。
假设我们现在有一组训练数据,需要训练一个模型(基于梯度的学习,不包括最近邻等方法)。在训练过程的最初,bias很大,因为我们的模型还没有来得及开始学习,也就是与“真实模型”差距很大。然而此时variance却很小,因为训练数据集(training data)还没有来得及对模型产生影响,所以此时将模型应用于“不同的”训练数据集也不会有太大差异。
而随着训练过程的进行,bias变小了,因为我们的模型变得“聪明”了,懂得了更多关于“真实模型”的信息,输出值与真实值之间更加接近了。但是如果我们训练得时间太久了,variance就会变得很大,因为我们除了学习到关于真实模型的信息,还学到了许多具体的,只针对我们使用的训练集(真实数据的子集)的信息。而不同的可能训练数据集(真实数据的子集)之间的某些特征和噪声是不一致的,这就导致了我们的模型在很多其他的数据集上就无法获得很好的效果,也就是所谓的overfitting(过学习)。
这就是最有代表性的R和Python的区别之一,统计社区出来的R更注重算法的理论正确性,但是一旦数据量大了运算性能可能成问题。而程序员为主体的Python社区更注重实际应用的性能考量,所以会取巧的修改算法牺牲模型性能。
另一方面,一些实际应用的结果表明,在cardinality非常大的情况下,直接把每个level编码成数字然后当做数值feature来用,其实效果并不会比严格按照categorical来使用差很多,这个缺少理论支持但是也值得一试。
除此之外,如果具体用的package真的必须要做encoding,那么除了one-hot,还可以考虑,binary,合并出现次数少的categorical level,embedding,以及用目标label均值替换categorical level等方法,来降低one-hot带来的过多额外feature的问题Sklearn或XGBoost 只能用one hot,因为它不支持直接操作categorical feature,one hot了以后相当于每个feature都是只能取两个值的numerical feature,用一组这样的feature来模拟一个categorical feature。
坏处就像上面说的,树很容易搞得很深,另外如果你用这种树做随机森林,每次分裂随机选择一部分feature的话,这个feature是被underrepresented的(这个feature的预测力被人为拆成若干份,每一份与其它feature竞争best split都会输),最后这个feature得到的importance会比实际值低。
可能无法在这个类别特征上进行切分。使用one-hot coding的话,意味着在每一个决策节点上只能用 one-vs-rest (例如是不是狗,是不是猫,等等) 的切分方式。当特征纬度高时,每个类别上的数据都会比较少,这时候产生的切分不平衡,切分增益(split gain)也会很小(比较直观的理解是,不平衡的切分和不切分几乎没有区别);
会影响决策树的学习。因为就算可以在这个类别特征进行切分,也会把数据切分到很多零散的小空间上,如图1左所示。而决策树学习时利用的是统计信息,在这些数据量小的空间上,统计信息不准确,学习会变差。但如果使用图1右边的切分方法,数据会被切分到两个比较大的空间,进一步的学习也会更好。
关于激活函数的选取,在LSTM中,遗忘门、输入门和输出门使用 Sigmoid函数作为激活函数;在生成候选记忆时,使用双曲正切函数tanh作为激活函数。值得注意的是,这两个激活函数都是饱和的也就是说在输入达到一定值的情况下,输出就不会发生明显变化了。如果是用非饱和的激活图数,例如ReLU,那么将难以实现门控的效果。
Sigmoid的输出在0-1之同,符合门控的物理定义,且当输入较大或较小时,其输出会非常接近1或0,从而保证该门开或关,在生成候选记亿时,使用tanh函数,是因为其输出在-1-1之间,这与大多数场景下特征分布是0中心的吻合。此外,tanh函数在输入为0近相比 Sigmoid函数有更大的梯度,通常使模型收敛更快。
激活函数的选择也不是一成不变的。例如在原始的LSTM中,使用的激活函数是 Sigmoid函数的变种,h(x)=2sigmoid(x)-1,g(x)=4 sigmoid(x)-2,这两个函数的范国分别是[-1,1]和[-2,2]。并且在原始的LSTM中,只有输入门和输出门,没有遗忘门,其中输入经过输入门后是直接与记忆相加的,所以输入门控g(x)的值是0中心的。后来经过大量的研究和实验,人们发现增加遗忘门对LSTM的性能有很大的提升且h(x)使用tanh比2 sigmoid(x)-1要好,所以现代的LSTM采用 Sigmoid和tanh作为激活函数。事实上在门控中,使用 Sigmoid函数是几乎所有现代神经网络模块的共同选择。例如在门控循环单元和注意力机制中,也广泛使用 Sigmoid i函数作为门控的激活函数。
此外,在一些对计算能力有限制的设备,诸如可穿戴设备中,由于 Sigmoid函数求指数需要一定的计算量,此时会使用0/1门让门控输出为0或1的离散值,即当输入小于阈值时,门控输出为0;当输入大于阈值时,输出为1。从而在性能下降不著的情况下,减小计算量。
参考资料:机器学习面试要点



 浙公网安备 33010602011771号
浙公网安备 33010602011771号