线性回归实现广告数据分析

一、 内容

使用matplotlib、numpy、sklearn.linear_model. LinearRegression，基于月度广告费用与销售费用数据，应用线性回归（Linera Regression） 算法，实现绘制广告费与销售额的最佳线性关系图。

二、 目标

• 掌握线性回归算法。
• 熟悉sklearn 线性回归相关API

三、 环境

• 操作系统：Windows7/Windows10、Ubuntu18.04
• 工具软件：Anaconda3 2019、Python3.6.13
• 硬件环境：无特殊要求
• 依赖第三方库:
  • numpy 1.19.5
  • pandas 1.1.5
  • matplotlib 3.3.4
  • scikit-learn 0.24.2

四、原理

1、LinearRegression

• 所在模块sklearn.linear_model.LinearRegression

• 官网API

• 参考API

线性回归（Linear Regression）是一种通过拟合自变量与因变量之 间最佳线性关系，来预测目标变量的方法。线性回归的类型包括简单线性回归和多元线性回归。简单一元线性回归使用一个自变量，通过拟合最佳线性关系来预测因变量，本质就是一条直线y=ax+b。多元线性回归使用多个独立变量，通过拟合最佳线性关系来预测因变量。

2、 scikit-learn

scikit-learn 是基于 Python 语言的机器学习工具。基本功能主要被分为六大部分：分类，回归，聚类，数据降维，模型选择和数据预处理。

1. 简单高效的数据挖掘和数据分析工具
2. 可供大家在各种环境中重复使用
3. 建立在 NumPy ，SciPy 和 matplotlib 上
4. 开源，可商业使用 - BSD许可证
5. 中文API地址

3、 广告数据集

某公司的月度广告费用与销售费用

五、 步骤

打开notebook 开发环境，新建ipynb文件，命名为实验2.3-线性回归实现广告数据分析.ipynb保存在当前项目根目录下的code文件夹中。

代码实现：

import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
# LinearRegression 普通最小二乘线性回归
from sklearn.linear_model import LinearRegression
from sklearn.utils import check_random_state


n = 16
rs = check_random_state(0)
X = rs.randint(1,100,size=(n,))#np.arange(n)
X.sort()
y = rs.randint(-20, 50, size=(n,)) + 50 * np.log(1 + np.arange(n))
y = [int(yy) for yy in y]
print("X:",X)
print("Y:",y)
model2 = LinearRegression()
# np.newaxis 的用法增加维度
model2.fit(X[:, np.newaxis], y)

m = model2.coef_[0] #线性回归问题的估计系数
b = model2.intercept_ #  线性模型中的独立项
print(' y = {0} * x + {1}'.format(m, b))

r2 = model2.score(X[:, np.newaxis], y)
print("r2:",r2)  # 打印r2指标取值约接近1拟合程度越好

# 绘图
plt.scatter(X, y,color='g')
plt.plot(X, model2.predict(X[:, np.newaxis]),color='k')
plt.show()

结果展示：

X: [10 13 22 37 45 48 59 65 66 68 68 71 84 88 89 89]
Y: [19, 60, 71, 74, 69, 89, 146, 130, 153, 144, 128, 123, 127, 125, 154, 150]
 y = 1.37939643679554 * x + 30.637280329657003
r2: 0.7861129941287246

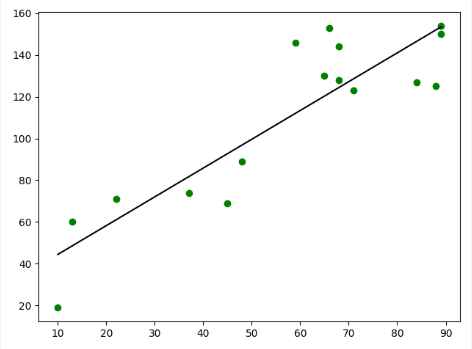
可以看到随着广告费用的增长，公司的销售额也在增加，但是他们并非是绝对的线性关系，而是趋于平均。上述线性回归模型的公式为：y=1.38×x+30.6，其中x表示广告费 用，y表示销售额。通过线性回归的公式就可以预测企业的销售额了， 例如回答“下一季度要提高销售额至200万元，那么广告费用需要投放多 少”等诸如此类问题。

六、 总结

线性回归：能拟合出特征数据之间最佳线性关系，实现预测。线性回归在生活中使用非常普遍，比如：生物统计学家高尔顿研究父母和子女身高的关系时发现：即使父母的身高都“极端”高，其子女不见得会比父母高，而是有“衰退”（Regression）至平均身高的倾向。