【算法】布隆过滤BitMap原理

一、问题引入

BitMap从字面的意思，很多人认为是位图，其实准确的来说，翻译成基于位的映射，怎么理解呢？
举一个例子，有一个无序有界int数组{1,2,5,7},初步估计占用内存44=16字节，这倒是没什么奇怪的，但是假如有10亿个这样的数呢，10亿4/(102410241024)=3.72G左右。如果这样的一个大的数据做查找和排序，那估计内存也崩溃了，有人说，这些数据可以不用一次性加载，那就是要存盘了，存盘必然消耗IO。我们提倡的是高性能，这个方案直接不考虑。

二、问题分析

如果用BitMap思想来解决的话，就好很多，那么BitMap是怎么解决的啊，如下：
一个byte是占8个bit，如果每一个bit的值就是有或者没有，也就是二进制的0或者1，如果用bit的位置代表数组值有还是没有，那么0代表该数值没有出现过，1代表该数组值出现过。不也能描述数据了吗？如下图：

 

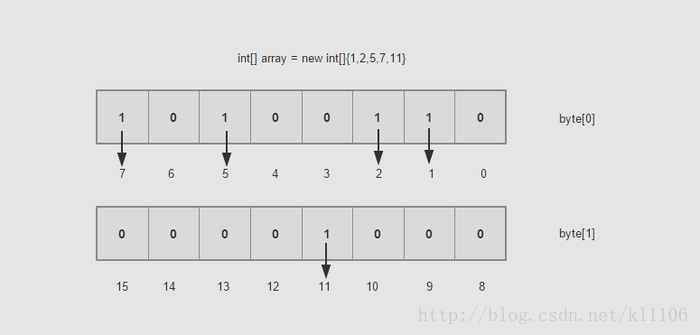
是不是很神奇，那么现在假如10亿的数据所需的空间就是3.72G/32了吧，一个占用32bit的数据现在只占用了1bit，节省了不少的空间，排序就更不用说了，一切显得那么顺利。这样的数据之间没有关联性，要是读取的，你可以用多线程的方式去读取。时间复杂度方面也是O(Max/n)，其中Max为byte[]数组的大小，n为线程大小。

三、应用与代码

如果BitMap仅仅是这个特点，我觉得还不是它的优雅的地方，接下来继续欣赏它的魅力所在。下面的计算思想其实就是针对bit的逻辑运算得到，类似这种逻辑运算的应用场景可以用于权限计算之中。
再看代码之前，我们先搞清楚一个问题，一个数怎么快速定位它的索引号，也就是说搞清楚byte[index]的index是多少，position是哪一位。举个例子吧，例如add(14)。14已经超出byte[0]的映射范围，在byte[1]范围之类。那么怎么快速定位它的索引呢。如果找到它的索引号，又怎么定位它的位置呢。Index(N)代表N的索引号，Position(N)代表N的所在的位置号。

Index(N) = N/8 = N >> 3;

Position(N) = N%8 = N & 0x07;

基于上面的分析，我们写一个简单的BitMap的算法如下：

public class BitMap {
    //保存数据的
    private byte[] bits;
    
    //能够存储多少数据
    private int capacity;
    
    
    public BitMap(int capacity){
        this.capacity = capacity;
        
        //1bit能存储8个数据，那么capacity数据需要多少个bit呢，capacity/8+1,右移3位相当于除以8
        bits = new byte[(capacity >>3 )+1];
    }
    
    public void add(int num){
        // num/8得到byte[]的index
        int arrayIndex = num >> 3; 
        
        // num%8得到在byte[index]的位置
        int position = num & 0x07; 
        
        //将1左移position后，那个位置自然就是1，然后和以前的数据做|，这样，那个位置就替换成1了。
        bits[arrayIndex] |= 1 << position; 
    }
    
    public boolean contain(int num){
        // num/8得到byte[]的index
        int arrayIndex = num >> 3; 
        
        // num%8得到在byte[index]的位置
        int position = num & 0x07; 
        
        //将1左移position后，那个位置自然就是1，然后和以前的数据做&，判断是否为0即可
        return (bits[arrayIndex] & (1 << position)) !=0; 
    }
    
    public void clear(int num){
        // num/8得到byte[]的index
        int arrayIndex = num >> 3; 
        
        // num%8得到在byte[index]的位置
        int position = num & 0x07; 
        
        //将1左移position后，那个位置自然就是1，然后对取反，再与当前值做&，即可清除当前的位置了.
        bits[arrayIndex] &= ~(1 << position); 


    }
    
    public static void main(String[] args) {
        BitMap bitmap = new BitMap(100);
        bitmap.add(7);
        System.out.println("插入7成功");
        
        boolean isexsit = bitmap.contain(7);
        System.out.println("7是否存在:"+isexsit);
        
        bitmap.clear(7);
        isexsit = bitmap.contain(7);
        System.out.println("7是否存在:"+isexsit);
    }
}