word2vec原理与代码
目录
前言
CBOW模型与Skip-gram模型
基于Hierarchical Softmax框架的CBOW模型
基于Negative Sampling框架的CBOW模型
负采样算法
结巴分词
word2vec
|
前言 |
word2vec当前主流实现有4种：基于Negative Sampling框架和基于Hierarchical Softmax框架的CBOW模型和Skip-gram模型。Negative Sampling是用来提高训练速度并改善所得词向量的质量。其不再使用复杂的哈夫曼树，而是利用简单的随机负采样，能大幅提高性能，因而Negative Sampling可作为Hierarchical Softmax的一种替代。本文主要介绍CBOW模型。
|
CBOW模型与Skip-gram模型 |
由图可见，两个模型都包含三层：输入层、投影层和输出层。前者是在已知当前词wt的上下文wt-2,wt-1,wt+1,wt+2的前提下预测当前词wt（左图）；后者相反，是在已知当前词wt的前提下，预测其上下文wt-2,wt-1,wt+1,wt+2。
对于CBOW和Skip-gram两个模型，word2vec给出了两套框架，他们分别基于Hierarchical Softmax和Negative Sampling来进行设计。
|
基于Hierarchical Softmax框架的CBOW模型 |
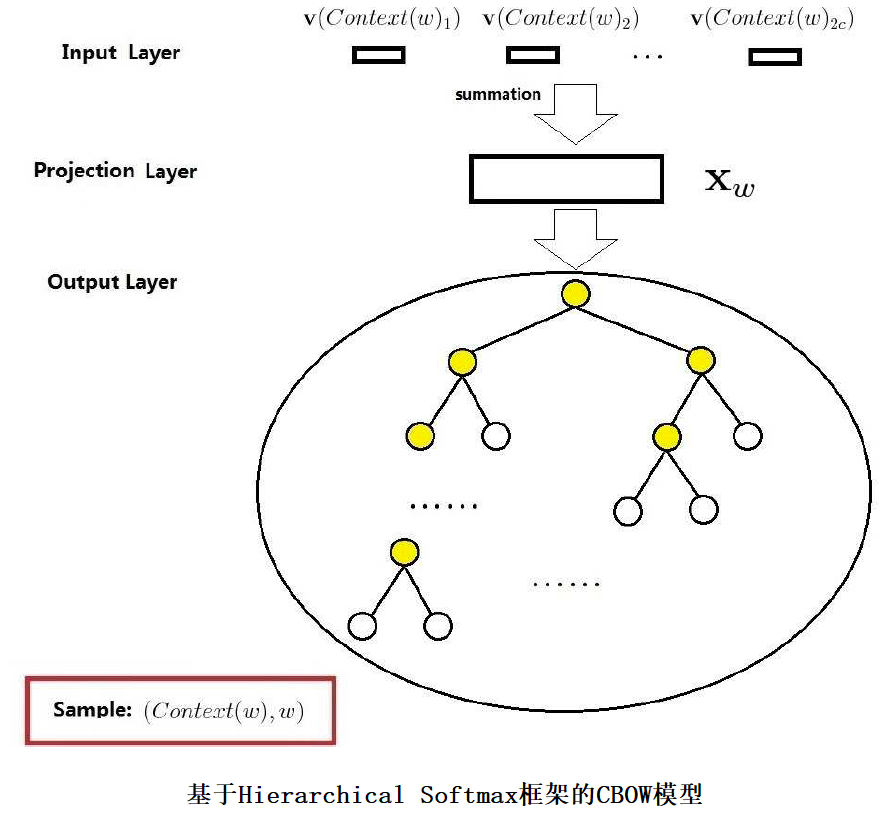
上图是基于Hierarchical Softmax框架的CBOW模型的网络结构，它包括3层：输入层、投影层和输出层。下面以样本((Context(w),w)为例(这里假设Context(w)由w前后各c个词构成)
下面对这三个层做简要说明：
1.输入层：包含(Context(w)中2c个词的词向量v(Context(w)1),v(Context(w)2),...,v(Context(w)2c)∈Rm。这里，m表示词向量的长度。
2.投影层：将输入层的2c个向量求和，即
3.输出层：输出层对应一棵二叉树，它以语料中出现过的词当叶节点，以各词在语料中出现的次数当权值构造出来的哈夫曼树。在这颗哈夫曼树中，叶节点有N(=|D|)个，分别对应词典D中的词。
对比以往的神经概率语言模型和CBOW模型主要有以下三种不同：
①(从输入层到投影层的操作)前者是通过首尾相连的拼接，后者是通过累加求和
②(隐藏层)前者有隐藏层，后者无隐藏层
③(输出层)前者是线性结构，后者是树形结构
在神经概率语言模型中，模型的大部分计算集中在隐藏层和输出层之间的矩阵向量运算，以及输出层上的softmax 归一化运算.而从上面的对比中可见，CBOW 模型对这些计算复杂度高的地方有针对性地进行了改变，首先，去掉了隐藏层，其次，输出层改用了Huffiman 树，从而为利用Hierarchical softmax 技术奠定了基础.
和传统机器学习算法一样，我们要定义一个优化目标，这里我们使用最大似然函数，即
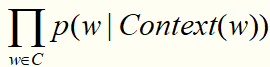
其中，C表示语料，Context(w)表示词w的上下文，即w周边的词的集合。语料C和词典D的区别：词典是从语料中抽取出来的，不存在重复的词；而语料是指所有的文本内容，包括重复的词。
举例：“一架从柏林飞往美国的客机悄无声息地降落在肯尼迪国际机场一个废弃的跑道上”
首先句子需要分词：一架、从、柏林、飞往、美国、的、客机、悄无声息、地、降落、在、肯尼迪、国际、机场、一个、废弃、的、跑道、上
先为词典中的每一个词向量进行随机初始化
计算语料中第1个词“一架”：将其上下文“从”、“柏林”的向量相加，然后就可以通过特定模式刻画出出现“一架”的概率p1。
计算语料中第2个词“从”：将其上下文“一架”、“柏林”、“飞往”的向量相加，然后就可以通过特定模式刻画出出现“从”的概率p2。
计算语料中第n个词“XXX”，将其上下文“AAA”、“BBB”、“CCC”、“DDD”的向量相加，然后就可以通过特定模式刻画出出现“XXX”的概率pn。
目标：最大化最大对数似然函数(将所有的p相乘然后取对数)。然后使用梯度下降法更新参数和词向量
下面详细介绍一下这个过程是如何工作的：
先说如何刻画在给定上下文的条件下出现某个词的概率p(w|Context(x))？答：需要用哈夫曼树和逻辑回归
首先建立哈夫曼树，非叶节点上都有一个未知向量，因为哈夫曼树是一个二叉树，每一次向下遍历只有向左和向右两个方向，即二分类。那么自然联想到用逻辑回归来做这个事情，每一次向左记为1；每一次向右记为0；
比如在给定了“足球”的上下文的条件下，我们当然希望模型预测出“足球”的概率最大，那我们就建立多个逻辑回归模型进行多次分类(向着“足球”行进)，然后，就找到优化目标了：最大化最大对数似然函数(将所有的p相乘然后取对数)。然后使用梯度下降法更新参数(哈夫曼树中非叶结点上都有一个未知向量的参数)和词向量(之前都是随机生成的)
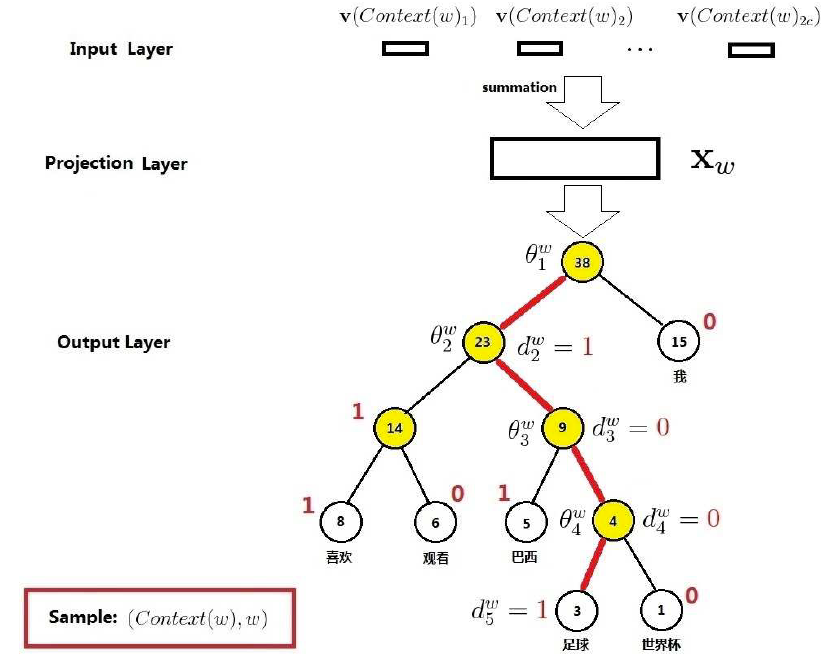
对于从根节点出发到达“足球”这个叶子节点所经历的4次二分类，将每次分类结果的概率写出来就是：
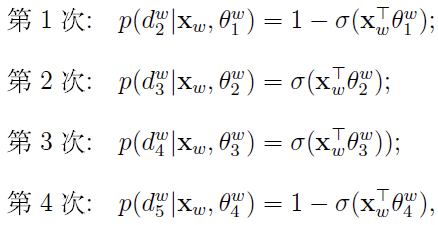
最优化目标，即对数似然函数是：
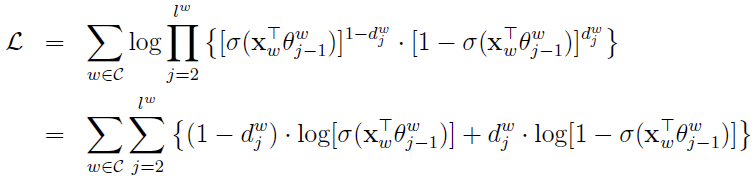
其中
是投影层计算出来的“足球”上下文向量的和，
就是哈夫曼非叶节点 j 上的向量。接下来就要更新Xw和
。
使用梯度上升法，更新未知参数：
为了简化，记
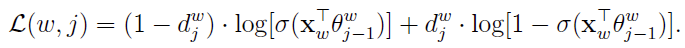
计算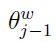
的梯度：
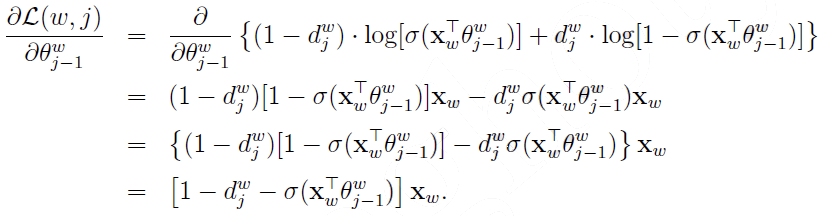
更新：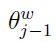
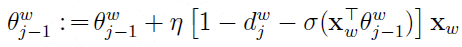
计算Xw的梯度：
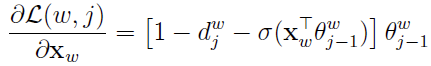
更新Xw：
|
基于Negative Sampling框架的CBOW模型 |
Negative Sampling是用来提高训练速度并改善所得词向量的质量。其不再使用复杂的哈夫曼树，而是利用简单的随机负采样，能大幅提高性能，因而Negative Sampling可作为Hierarchical Softmax的一种替代。
在Hierarchical Softmax框架里我们用了哈夫曼树作为构造优化目标的桥梁，但是效率较低。Negative Sampling(负采样)框架是如何作为构造优化目标的桥梁的呢？
负采样的思想通俗讲就是：还是用“足球”的例子，比如已经给定了“足球”的上下文，那我们需要让模型预测为“足球”的概率最大，预测为其他词(负样本)的概率较小。负采样技术就是随机的从词典里抽一些不是“足球”的词。因此优化目标就是让他是“足球”的概率最大，是采样出来的其他负样本的概率较小。
因此，优化目标是最大化g(w)：
其中，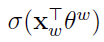
表示上下文为
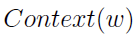时，预测中心词为w的概率，而
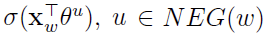则表示当上下文为
时，预测中心词为u的概率。从形式上看最大化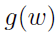
，相当于最大化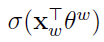，同时最小化所有的
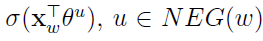。这不正是我们希望的吗？增大正样本的概率同时降低负样本的概率。于是，对于一个给定的语料库C，函数
就可以作为整体优化的目标。为了计算方便，对G取对数，最终的目标函数就是：
为了推倒方便，简记
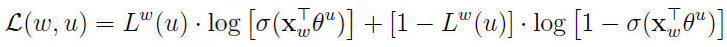
接下来利用梯度上升法进行优化，首先考虑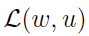
关于
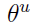的梯度计算
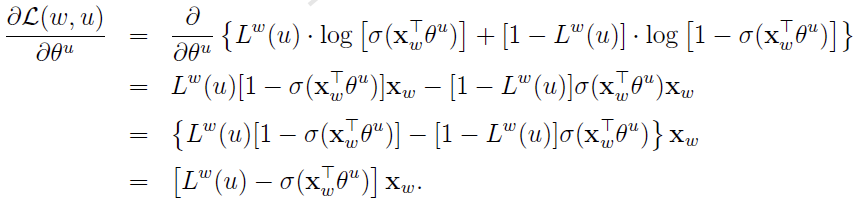
于是，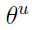
的更新公式可写为
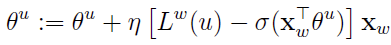
接下来考虑
关于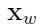
的梯度，同样利用
中
和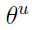的对称性，有
于是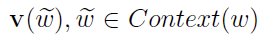
的更新公式为
|
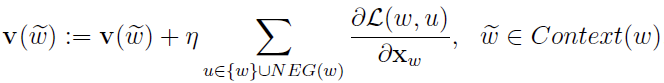
负采样算法 |
负采样是一个很重要的环节，对于一个给定的词w，如何生成NEG(w)呢？
词典D中的词在语料C中出现的次数有高有低，对于那些高频词，被选为负样本的概率就应该较大。这就是我们对采样过程的大致要求，本质就是一个带权采样问题。
|
结巴分词 |
word2vec模型要求的输入是以空格分割的有顺序的剧组，如：一架 从 柏林 飞往 美国 的 客机 悄无声息 地 降落 在 肯尼迪 国际 机场 一个 废弃 的 跑 上。而我们往往获得的训练集都是一些文章，因此需要先使用工具将其分词。结巴分词是一个不错的中文分词的工具。下面这篇文章介绍其使用方法
https://www.jianshu.com/p/e8b5d01ca073
|
word2vec |
创建模型：
# -*- coding: utf-8 -*- from gensim.models import word2vec import logging logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO) sentences = word2vec.Text8Corpus("b.txt") # 加载语料 model = word2vec.Word2Vec(sentences, size=200) # 默认window=5 model.save(u"c.model")
其中b是语料库，形式为：
使用模型：
# -*- coding: utf-8 -*- from gensim.models import word2vec import logging logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO) model = word2vec.Word2Vec.load(u"c.model") y2 = model.most_similar(positive=[u"中国",u"战争"],topn=20) # 20个最相关的 for i in y2: print i[0], # 抗日战争 国人 中日战争 侵略战争 二战 国家 我国 本国 中华民族 鸦片战争 抗战 南京大屠杀 文化大革命 别国 战败国 中日 当今世界 美国 国民性 解放战争 y2 = model.most_similar(positive=[u"美国",u"战争"],topn=20) # 20个最相关的 for i in y2: print i[0], # 二战 越战 伊战 越南战争 侵略战争 内战 第二次世界大战 南北战争 国家 二次世界大战 二次大战 朝鲜战争 太平洋战争 当今世界 抗日战争 米国 独立战争 殖民主义 霸权主义 强权政治
