强化学习原理源码解读003：Actor-Critic和A2C

在强化学习中，可以分为如下图所示的两种框架。基于Policy-based框架的算法有Policy Gradient(Sutton 2000)、PPO、PPO2等；基于Value-based框架的算法有DQN(Mnih 2013)、DDQN等；结合这两种框架的算法有Actor-Critic(VR Konda 2000在Policy Gradient之后)、A2C、A3C(2016 DeepMind)、Rainbow等。

Policy-based框架的缺点

只使用参数化的策略。通过仿真直接估计累计回报值对actor参数的梯度，并向改进方向更新参数。这种方法的一个可能的缺点是梯度估计量可能有一个大的方差。此外，随着策略的变化，对新的梯度的估计独立于过去的估计。因此，没有“学习”，也就是旧信息的积累和巩固。

返回目录

Valued-based框架的缺点

完全依赖于值函数近似。通过学习Bellman方程的近似解，然后有希望规定一个接近最优的策略。这些方法是间接的，因为它们不试图直接优化策略空间。这种类型的方法可以成功地构造一个值函数的“好的”近似值，但在结果策略的接近最优性方面缺乏可靠的保证。另外对于连续型动作不宜求解。

返回目录

Actor-Critic结合

Actor-Critic算法的学习过程克服了Policy-based框架下计算得到的回报值方差大的问题，大部分情况下，也可以推广到任意状态和动作空间的情况下。

返回目录

算法流程

下面将整个算法分解为下面几个小问题进行详述：

■向Policy Gradient中加入baseline

■Q网络和V网络的定义

■A2C (Advantage Actor-Critic)

■A2C损失函数的构建

返回目录

向Policy Gradient中加入baseline

结合上图，如果所有的动作都会得到正的回报，会存在一个问题，假设有三个动作可以执行abc：

在理想情况下，做梯度上升，会把采用abc的几率都拉高，但是他们对应的R是不一样的，R小的，上升的就小，权重大的就上升的多。因为最终几率的和等于1，所以上升的多的才会上升，上升的小的会下降。

但是在实际过程中，我们做的是采样，那就意味着有的动作会采样不到（有可能是一个很好的动作），那么就会恶性循环，接下来采用这个动作的几率会越来越小。

解决方法：

回报减去一个基础值baseline，让权重有正有负

比如b是一个让回报增加很小的动作（也就是一个比较差的动作），那么他的权重很大程度是小于baseline的，那么梯度上升更新之后，采用b的概率会下降。嵌入baseline后的梯度值如下所示：

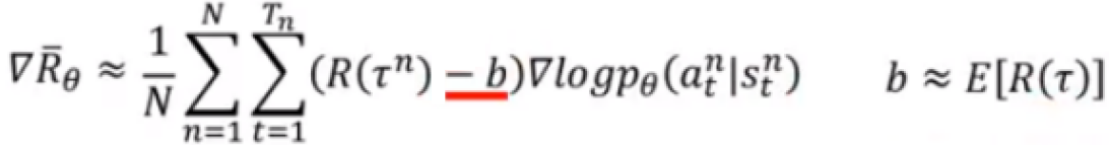
当然也可以加入折扣因子：

返回目录

Q网络和V网络的定义

这个b可以使用状态价值函数V网络来计算，因为他就是累计回报值这个随机变量数学期望，红色方框内相减之后就会有正有负，达到我们想要的效果。

蓝色下划线部分是执行了a之后的累计回报值的期望可以由Q网络计算。

这时需要学习的网络就有三个：策略网络、Q网络和V网络，如果直接这样做的话会因为网络参数过多，导致优化难度变大的问题，A2C算法就解决了这个问题。

返回目录

A2C (Advantage Actor-Critic)

A2C算法指出，我们可以在忍受一定方差的影响的情况下，只估测V，然后用V表示Q

所以我们的网络结构变成：

返回目录

A2C损失函数的构建

返回目录

源码实现

这里做了一些简练：去掉了分别学习目标网络、去掉了Replay Buffer

import gym
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.distributions import Categorical
import matplotlib.pyplot as plt
#Hyperparameters
learning_rate = 0.0002
gamma         = 0.98
n_rollout     = 10

class ActorCritic(nn.Module):
    def __init__(self):
        super(ActorCritic, self).__init__()
        self.data = []
        
        self.fc1 = nn.Linear(4,256)
        self.fc_pi = nn.Linear(256,2)
        self.fc_v = nn.Linear(256,1)
        self.optimizer = optim.Adam(self.parameters(), lr=learning_rate)
        
    def pi(self, x, softmax_dim = 0):
        x = F.relu(self.fc1(x))
        x = self.fc_pi(x)
        prob = F.softmax(x, dim=softmax_dim)
        return prob
    
    def v(self, x):
        x = F.relu(self.fc1(x))
        v = self.fc_v(x)
        return v
    
    def put_data(self, transition):
        self.data.append(transition)
        
    def make_batch(self):
        s_lst, a_lst, r_lst, s_prime_lst, done_lst = [], [], [], [], []
        for transition in self.data:
            s,a,r,s_prime,done = transition
            s_lst.append(s)
            a_lst.append([a])
            r_lst.append([r/100.0])
            s_prime_lst.append(s_prime)
            done_mask = 0.0 if done else 1.0
            done_lst.append([done_mask])
        
        s_batch, a_batch, r_batch, s_prime_batch, done_batch = torch.tensor(s_lst, dtype=torch.float), torch.tensor(a_lst), \
                                                               torch.tensor(r_lst, dtype=torch.float), torch.tensor(s_prime_lst, dtype=torch.float), \
                                                               torch.tensor(done_lst, dtype=torch.float)
        self.data = []
        return s_batch, a_batch, r_batch, s_prime_batch, done_batch
  
    def train_net(self):
        s, a, r, s_prime, done = self.make_batch()
        td_target = r + gamma * self.v(s_prime) * done
        delta = td_target - self.v(s)
        
        pi = self.pi(s, softmax_dim=1)
        pi_a = pi.gather(1,a)
        loss = -torch.log(pi_a) * delta.detach() + F.smooth_l1_loss(self.v(s), td_target.detach())

        self.optimizer.zero_grad()
        loss.mean().backward()
        self.optimizer.step()         
      
def main():  
    env = gym.make('CartPole-v1')
    model = ActorCritic()    
    print_interval = 20
    score = 0.0
    x = []
    y = []

    for n_epi in range(5000):
        done = False
        s = env.reset()
        while not done:
            for t in range(n_rollout):
                prob = model.pi(torch.from_numpy(s).float())
                m = Categorical(prob)
                a = m.sample().item()
                s_prime, r, done, info = env.step(a)
                model.put_data((s,a,r,s_prime,done))
                
                s = s_prime
                score += r
                
                if done:
                    break                     
            
            if score < 500 * print_interval:
                model.train_net()
            else:
                print(score)
            
        if n_epi%print_interval==0 and n_epi!=0:
            print("# of episode :{}, avg score : {:.1f}".format(n_epi, score/print_interval))
            x.append(n_epi)
            y.append(score / print_interval)
            score = 0.0
    env.close()
    plt.plot(x, y)
    plt.savefig('pic_saved/res_A2C.jpg')
    plt.show()

if __name__ == '__main__':
    main()

View Code

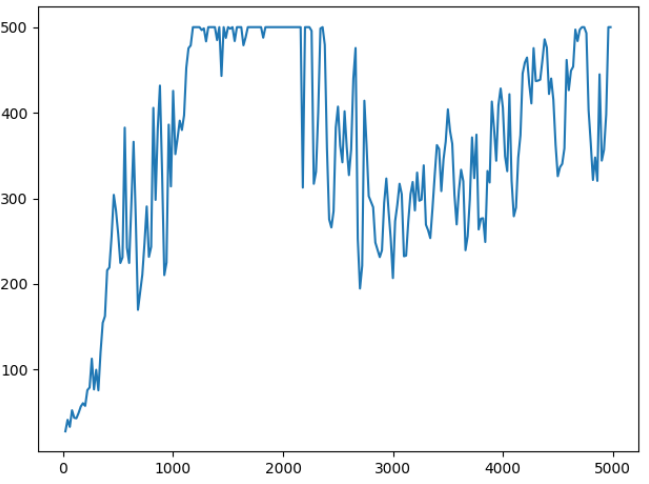
横坐标表示训练轮数，纵坐标表示智能体得分的能力（满分500分）

返回目录

参考资料

https://github.com/seungeunrho/minimalRL

https://www.bilibili.com/video/BV1UE411G78S?from=search&seid=10996250814942853843

paper:Actor-Critic Algorithms

paper:Asynchronous Methods for Deep Reinforcement Learning

返回目录

posted @ 2020-10-01 17:30 黎明程序员阅读(3409) 评论(1) 编辑收藏举报

刷新页面返回顶部

目录

公告