强化学习原理源码解读002:DQN
目录
Policy based方法 vs Value based方法
策略网络
算法总体流程
如何通过对回归任务的优化来更新Q网络
为什么不可以同时更新Q网络和目标网络
为什么要使用带有探索策略的Q函数
探索策略的数学表达
ReplayBuffer的作用
Q值被高估的问题
源码实现
参考资料
DQN是Deep Q Network的缩写,由Google Deep mind 团队提出。
|
Policy based方法 vs Value based方法 |
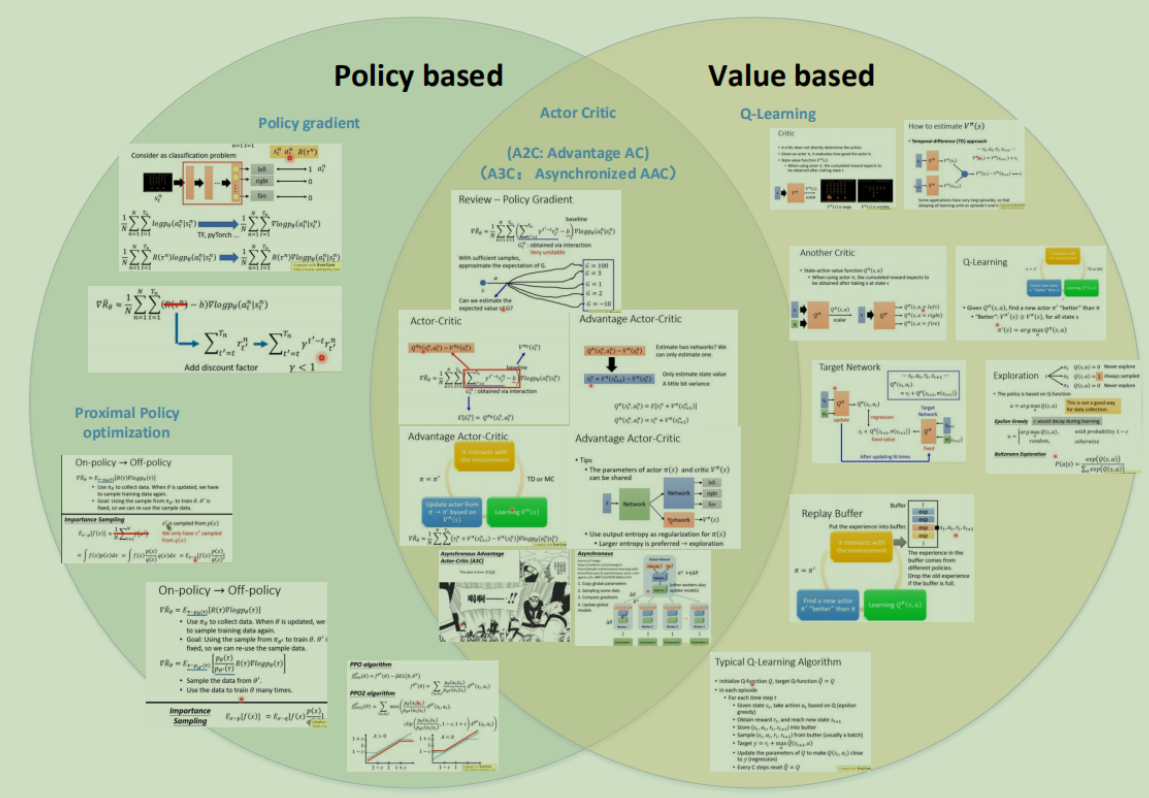
上一篇文章中提到的Policy Gradient属于Policy based的RL学习方法。
本文介绍的DQN属于Value based的RL学习方法。
两者区别:
Policy based是直接对累计奖励值进行最大化求解,在实做过程中,在很多任务中是训练不出比较好的智能体的;
而Value based方法是不直接对累计奖励值进行最大化求解,而是设置一个价值函数(状态或动作)来评价当前智能体到最后获得奖励值的期望,通过这种评价,再建立优化方案,从而达到对总体较优累计奖励值的求解。状态价值函数(State value)记为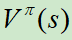 ,动作价值函数(State-action value)记为
,动作价值函数(State-action value)记为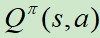 。
。
|
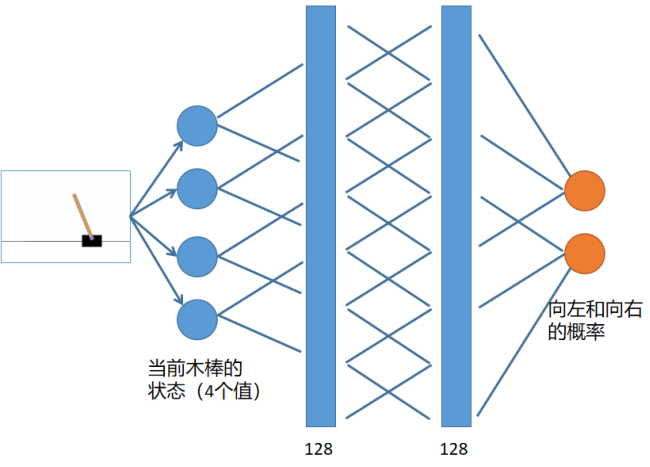
策略网络 |
self.fc1 = nn.Linear(4, 128)
self.fc2 = nn.Linear(128, 128)
self.fc3 = nn.Linear(128, 2)
|
算法总体流程 |

我们针对其中的几个要点进行展开:
■如何通过对回归任务的优化来更新Q网络
■为什么不可以同时更新Q网络和目标网络
■为什么要使用带有探索策略的Q函数
■探索策略的数学表达
■ReplayBuffer的作用
■Q值被高估的问题
|
如何通过对回归任务的优化来更新Q网络 |
假设我们收集到的某一笔数据为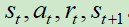 。
。
原始Q网络计算在状态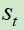 下执行动作
下执行动作 ,产生输出
,产生输出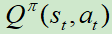 。
。
目标Q网络计算在状态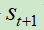 下执行动作
下执行动作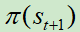 ,产生输出
,产生输出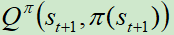 。
。
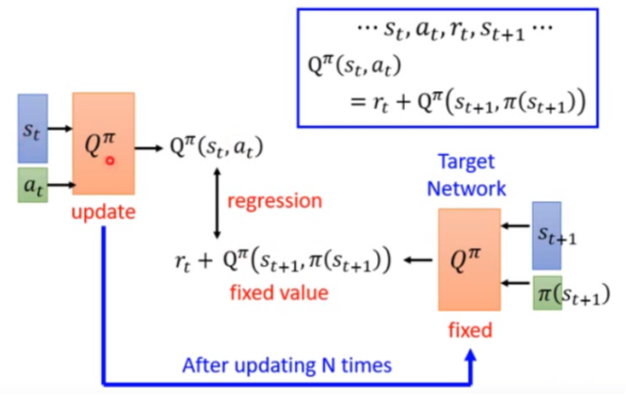
那么,就根据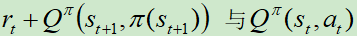 构建适用于回归的损失函数,更新时只更新原始Q网络,一段时间之后使用原始Q网络的参数覆盖目标Q网络 。
构建适用于回归的损失函数,更新时只更新原始Q网络,一段时间之后使用原始Q网络的参数覆盖目标Q网络 。
|
为什么不可以同时更新Q网络和目标网络 |
实验表明,同时更新两个网络会出现学习不稳定的情况。
|
为什么要使用带有探索策略的Q函数 |
当我们使用Q函数的时候,我们的π完全依赖于Q函数,穷举每一个a,看哪一个可以让Q最大。
这和policy Gradient不一样,在做PG的时候,我们输出是随机的,我们输出一个动作的分布,然后采样一个动作,所以在PG里每一次采取的动作是有随机性的。
很显然,刚开始估出来的Q函数是可靠的,假设有一个动作得到过奖励,那未来会一直采样这个动作。
例子1:你去了一个餐厅,点了一盘椒麻鸡,感觉好吃,以后去这个餐厅就一直点椒麻鸡,就不去探索是不是有更好吃的东西了。
例子2:玩贪吃蛇时,某一次向上走吃到了一个星星,那他以后就一直认为向上走是最好的,以至于很快就撞墙死掉。
|
探索策略的数学表达 |
列举两种方式:
方式一:Epsilon-Greedy
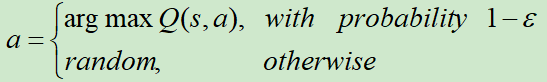
ε会随着时间的推移,逐渐变小。因为刚开始的时候需要更多的探索,当Q学习得比较不错的时候,就可以减少探索的概率。
方式二:Boltzmann Exploration
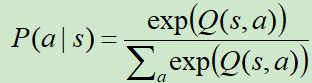
刚开始是一个均匀分布,后来价值高的动作采样到的概率越来越高。
其实还有比较高级的Noisy Net的方式
|
ReplayBuffer的作用 |
现在有一个智能体π和环境做互动来收集数据,我们会把所有的数据放在一个buffer里面,假设里面可以存5w个资料,每一笔资料就是一个四元组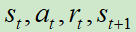 。
。
这里面的数据,可能来自于不同的策略。这个buffer只有在装满之后才会把旧的资料丢弃。
更新Q函数时,就从buffer中随机抽一个batch,然后去训练更新。
现在其实就变成了off-policy的,因为我们的Q本来要观察π的价值的,但是存在buffer里的经验,不是统统来自于π,有一些是过去的π遗留下来的。
好处:
1.在做强化学习的时候,往往耗时的是在于和环境做互动,训练的过程往往速度比较快,用了buffer可以减少和环境做互动的次数,因为在做训练的时候,经验不需要统统来自某一个π,一些过去的经验也可以放在buffer里被使用很多次。
2.在训练网络的时候,我们希望一个batch里面的数据越不同越好,如果batch里的数据都是同样性质的,训练下去是容易坏掉的。
问题:我们明明是要观察π的价值,里面混杂了一些不是π的经验,到底有没有关系?
一个简单的解释:这些π差的并不多,太老会自动舍弃的,所以没有关系。
|
Q值被高估的问题 |
在算target的时候,我们实际上在做的事情是,看哪一个a可以得到最大的Q值,就把他加上去作为target,假设有某一个动作他得到的值是被高估的,所以很大概率会选到那些值被高估的动作的值当做max的结果,再加上rt当做target,所以target总会太大。
解决方法:
最简单的方式就是对target的乘以一个小数
复杂的做法:
Double DQN
|
源码实现 |
代码

import gym import collections import random import torch import torch.nn as nn import torch.nn.functional as F import torch.optim as optim import matplotlib.pyplot as plt #Hyperparameters learning_rate = 0.0005 gamma = 0.98 buffer_limit = 50000 batch_size = 32 class ReplayBuffer(): def __init__(self): self.buffer = collections.deque(maxlen=buffer_limit) def put(self, transition): self.buffer.append(transition) def sample(self, n): mini_batch = random.sample(self.buffer, n) s_lst, a_lst, r_lst, s_prime_lst, done_mask_lst = [], [], [], [], [] for transition in mini_batch: s, a, r, s_prime, done_mask = transition s_lst.append(s) a_lst.append([a]) r_lst.append([r]) s_prime_lst.append(s_prime) done_mask_lst.append([done_mask]) return torch.tensor(s_lst, dtype=torch.float), torch.tensor(a_lst), \ torch.tensor(r_lst), torch.tensor(s_prime_lst, dtype=torch.float), \ torch.tensor(done_mask_lst) def size(self): return len(self.buffer) class Qnet(nn.Module): def __init__(self): super(Qnet, self).__init__() self.fc1 = nn.Linear(4, 128) self.fc2 = nn.Linear(128, 128) self.fc3 = nn.Linear(128, 2) def forward(self, x): x = F.relu(self.fc1(x)) x = F.relu(self.fc2(x)) x = self.fc3(x) return x def sample_action(self, obs, epsilon): out = self.forward(obs) coin = random.random() if coin < epsilon: return random.randint(0,1) else : return out.argmax().item() def train(q, q_target, memory, optimizer): for i in range(10): s,a,r,s_prime,done_mask = memory.sample(batch_size) q_out = q(s) q_a = q_out.gather(1,a) max_q_prime = q_target(s_prime).max(1)[0].unsqueeze(1) target = r + gamma * max_q_prime * done_mask loss = F.smooth_l1_loss(q_a, target) optimizer.zero_grad() loss.backward() optimizer.step() def main(): env = gym.make('CartPole-v1') q = Qnet() q_target = Qnet() q_target.load_state_dict(q.state_dict()) memory = ReplayBuffer() x = [] y = [] print_interval = 20 score = 0.0 optimizer = optim.Adam(q.parameters(), lr=learning_rate) for n_epi in range(5000): epsilon = max(0.01, 0.08 - 0.01*(n_epi/200)) #Linear annealing from 8% to 1% s = env.reset() done = False while not done: a = q.sample_action(torch.from_numpy(s).float(), epsilon) s_prime, r, done, info = env.step(a) done_mask = 0.0 if done else 1.0 memory.put((s,a,r/100.0,s_prime, done_mask)) s = s_prime score += r if done: break if memory.size()>2000 and score<500*print_interval: train(q, q_target, memory, optimizer) if n_epi%print_interval==0 and n_epi!=0: q_target.load_state_dict(q.state_dict()) x.append(n_epi) y.append(score / print_interval) print("n_episode :{}, score : {:.1f}, n_buffer : {}, eps : {:.1f}%".format( n_epi, score/print_interval, memory.size(), epsilon*100)) score = 0.0 env.close() env.close() plt.plot(x, y) plt.savefig('pic_saved/res_dqn.jpg') plt.show() if __name__ == '__main__': main()
效果如下图所示,横坐标表示训练轮数,纵坐标表示智能体平均得分,游戏满分500分
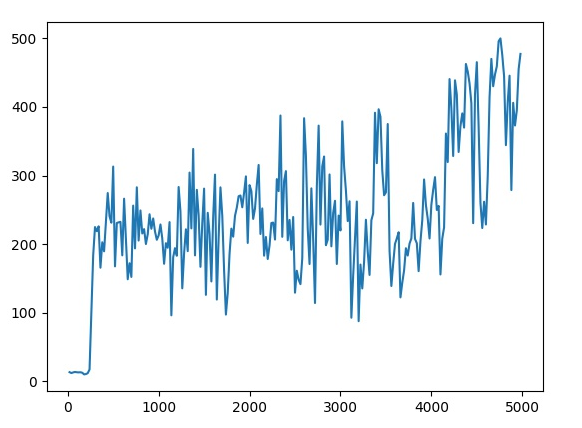
|
参考资料 |
https://github.com/seungeunrho/minimalRL
https://www.bilibili.com/video/BV1UE411G78S?from=search&seid=10996250814942853843





