强化学习原理源码解读001:Policy Gradient
目录
强化学习中的关键概念
游戏案例
策略网络
策略网络的训练
源码实现
效果演示
参考资料
本文不再维护,请移步最新博客:
https://zhuanlan.zhihu.com/p/408239932
|
强化学习中的关键概念 |
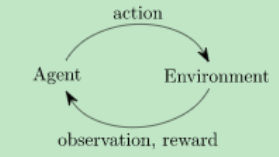
智能体(Agent):也就是我们的机器人,它内部有一个策略网络,策略网络接收一个可观测状态(observation)作为输入,产生一个动作(action)作为输出。
环境(Environment):也就是智能体与之交互的环境,它接收智能体的输入后,会发生改变,同时会计算智能体动作的奖励值(reward)。
|
游戏案例 |
强化学习技术可以应用在很多领域,比如:内容推荐、广告投放和机器人控制等等,另外强化学习技术在竞技游戏中的应用也非常有效,最知名的就有AlphaGo(DeepMind)、DotaAI(OpenAI)和王者荣耀的悟空AI(腾讯)等等。
在本案例中,我们针对https://gym.openai.com/中的一个简单游戏进行分析

这是一个平衡杆游戏,人控制滑块左右移动,保证上面木棒不倒下来
https://gym.openai.com/envs/CartPole-v1/
|
策略网络 |
使用了全连接网络作为策略网络
self.fc1 = nn.Linear(4, 128)
self.fc2 = nn.Linear(128, 2)

游戏初始的时候,环境会产生一个初始值(4个值,滑块的位置,滑块速度,木棒的角度,木棒尖端的速度)。
策略网络接收环境的输入,前馈,得到一个向左和向右的概率向量,依照概率选择一个动作,执行,如果木棒不会倒,就奖励1分。
环境接收动作后,发生改变,以此类推,直到杆子的倾斜角度超过一定阈值,游戏结束。
|
策略网络的训练 |
第一步,收集智能体和环境的交互数据
假设某一个Trajectory中收集一笔数据:![]()
那么参数为θ的策略网络产生该Trajectory的概率为:![]()
累计回报值定义为:![]()
强化学习的目标就是最大化累计回报值的期望值:![]()
那么,重点就在于计算![]() 的梯度值:
的梯度值:![]()
对θ微分时,R(τ)不需要微分,因为τ对应的R(τ)是不会变化的,或者说R(τ)和θ是没有关系的
由公式![]() ,可得
,可得![]()
改为期望的形式:![]()
使用采样代替期望值:![]() ,其中,N表示数据量
,其中,N表示数据量
展开 τ :![]() ,pθ(s1)大部分情况下都是固定值,可以忽略不计。
,pθ(s1)大部分情况下都是固定值,可以忽略不计。
在本文中,我们每收集一笔数据τ,就更新一次网络,也就是SGD的方式,那么可以去掉和N有关的项,简化为:![]()
同时,可以为R(τ)加一个折扣因子:![]()
进行梯度上升,让R越来越大:![]()
在pytorch实践中,我们无需手工梯度,只需要定义好损失函数即可:![]()
PS:这就是policy Gradient的技巧。这里留给读者一个思考题:既然我们已经知道pytorch无需手动求导,那为什么还要费力先求梯度,然后再还原回去呢?
该代码明显就是一个on-policy的方法,因为我们是:先收集数据,然后更新网络,再收集数据,再更新网络的方式。
|
源码实现 |
代码为

import gym import torch import torch.nn as nn import torch.nn.functional as F import torch.optim as optim from torch.distributions import Categorical import matplotlib.pyplot as plt import time #Hyperparameters learning_rate = 0.0002 gamma = 0.98 f_out = open("log.txt","w",encoding="utf-8") class Policy(nn.Module): def __init__(self): super(Policy, self).__init__() self.data = [] self.fc1 = nn.Linear(4, 128) self.fc2 = nn.Linear(128, 2) self.optimizer = optim.Adam(self.parameters(), lr=learning_rate) def forward(self, x): x = F.relu(self.fc1(x)) x = F.softmax(self.fc2(x), dim=0) return x def put_data(self, item): self.data.append(item) def train_net(self): R = 0 loss_prob = 0 self.optimizer.zero_grad() for r, prob in self.data[::-1]: R = r + gamma * R loss = -torch.log(prob) * R loss_prob += loss loss.backward() # f_out.write(f'{"-" * 50},{loss_sum/len(self.data[::-1])}\n') self.optimizer.step() self.data = [] def main(): env = gym.make('CartPole-v1') pi = Policy() score = 0.0 x = [] y = [] print_interval = 20 for n_epi in range(5000): s = env.reset() done = False while not done: # CartPole-v1 forced to terminates at 500 step. # env.render() prob = pi(torch.from_numpy(s).float()) m = Categorical(prob) a = m.sample() s_prime, r, done, info = env.step(a.item()) pi.put_data((r,prob[a])) s = s_prime score += r pi.train_net() # time.sleep(2) if n_epi%print_interval==0 and n_epi!=0: print("# of episode :{}, avg score : {}".format(n_epi, score/print_interval)) x.append(n_epi) y.append(score/print_interval) f_out.write("# of episode :{}, avg score : {}\n".format(n_epi, score/print_interval)) score = 0.0 torch.save(pi, 'model.pkl') env.close() plt.plot(x,y) plt.savefig('res.jpg') plt.show() if __name__ == '__main__': main()
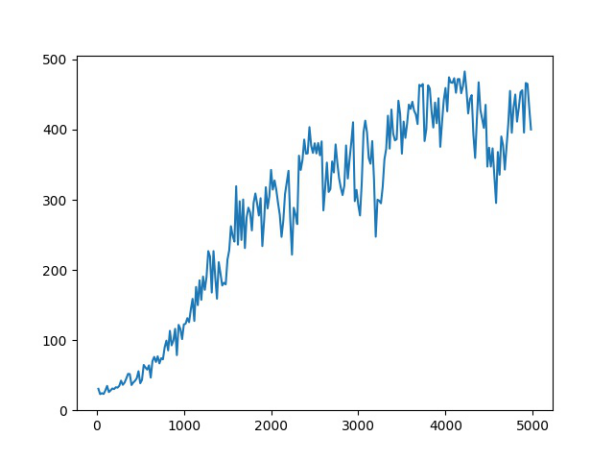
PS:这个游戏超过500分就是自动结束,横坐标是学习轮数,纵坐标是智能体的当前能获取的分数均值
|
效果演示 |
下图是经过100轮训练的智能体的玩游戏过程,可以看到,很快就会游戏结束
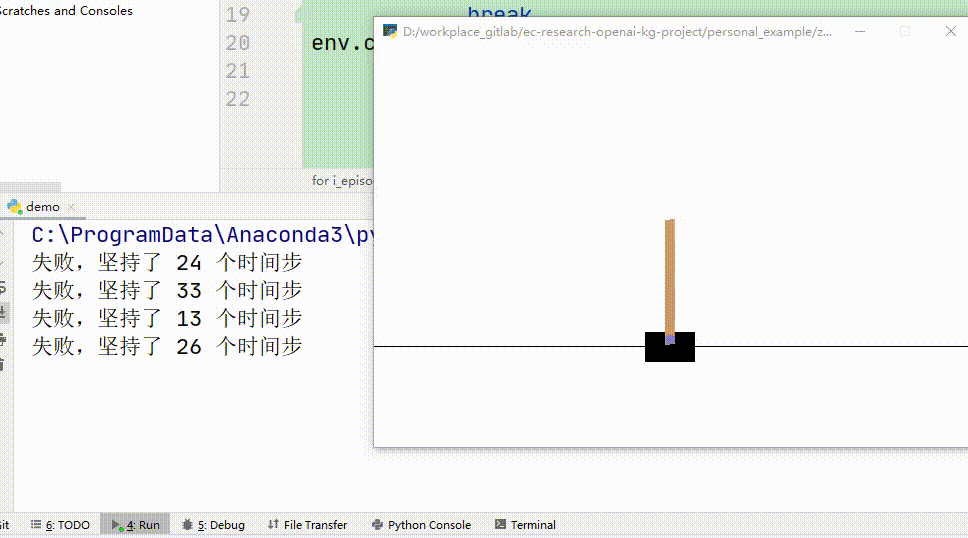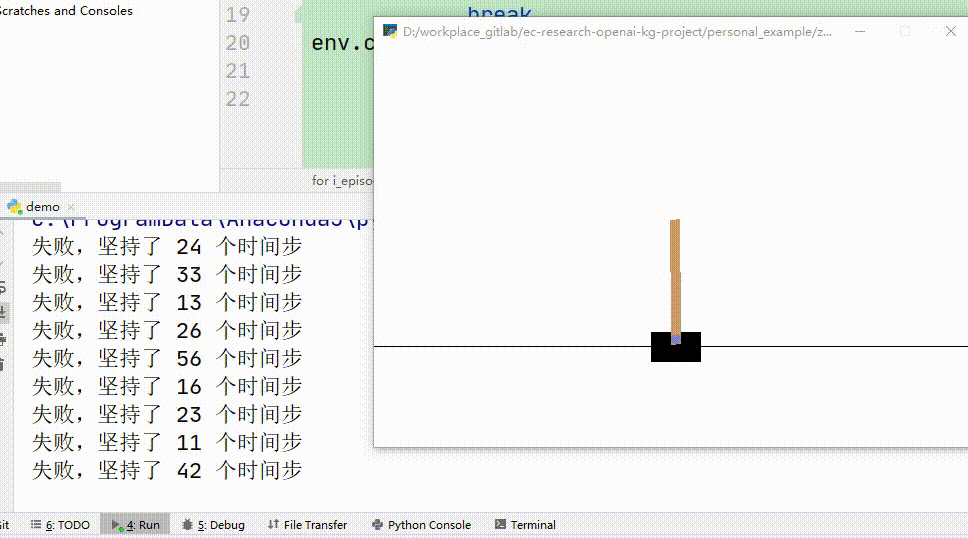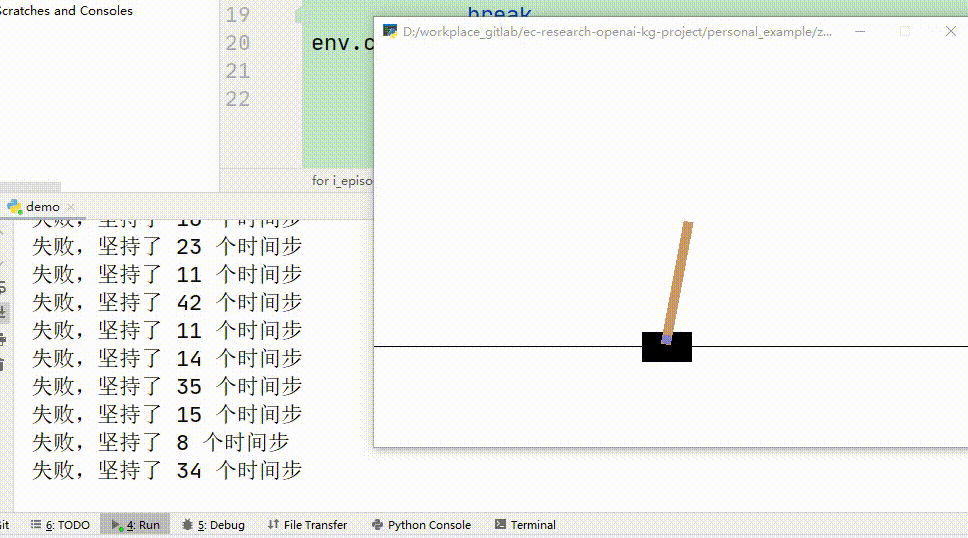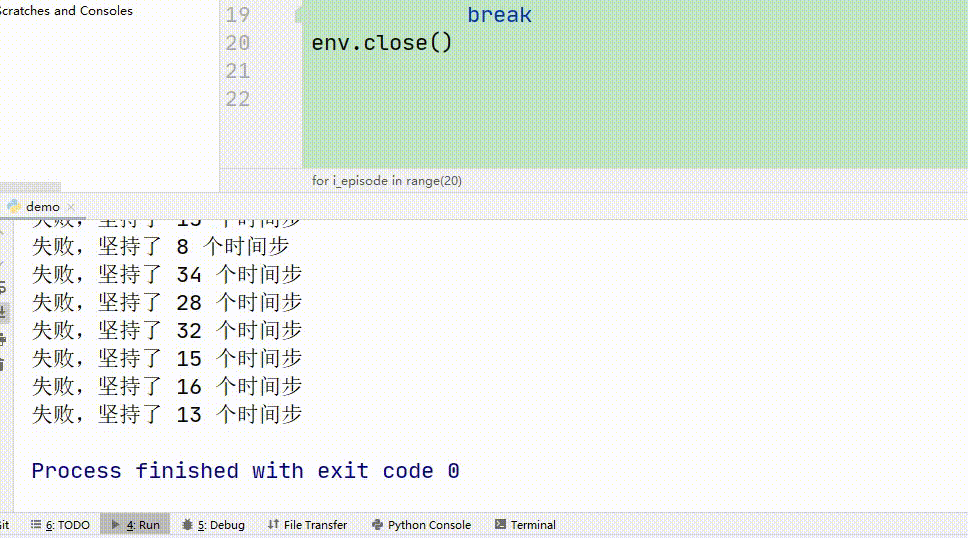
下图是经过5000训练的智能体的玩游戏过程,可以看到,他几乎都可以玩到满分

演示代码为:

import gym import torch from torch.distributions import Categorical from REINFORCE import Policy pi = torch.load('model.pkl') env = gym.make('CartPole-v1') for i_episode in range(20): observation = env.reset() for t in range(10000): env.render() prob = pi(torch.from_numpy(observation).float()) m = Categorical(prob) action = m.sample() observation, reward, done, info = env.step(action.item()) if done: print("失败,坚持了 {} 个时间步".format(t+1)) break env.close()
|
参考资料 |
https://github.com/seungeunrho/minimalRL
https://www.bilibili.com/video/BV1UE411G78S?from=search&seid=10996250814942853843


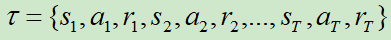
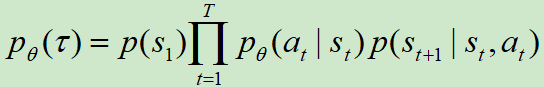
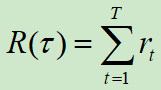
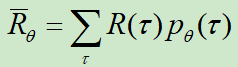
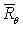 的梯度值:
的梯度值:
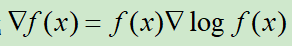 ,可得
,可得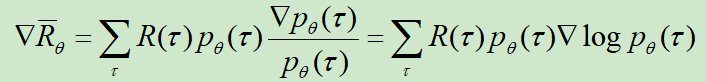
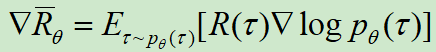
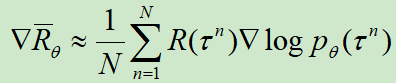 ,其中,N表示数据量
,其中,N表示数据量 ,pθ(s1)大部分情况下都是固定值,可以忽略不计。
,pθ(s1)大部分情况下都是固定值,可以忽略不计。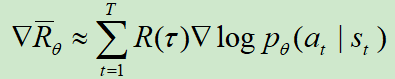

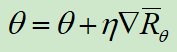
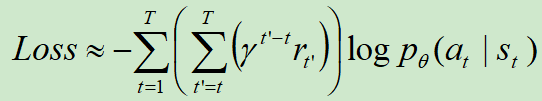


 浙公网安备 33010602011771号
浙公网安备 33010602011771号