深度学习面试题05：激活函数sigmod、tanh、ReLU、LeakyRelu、Relu6
目录
为什么要用激活函数
sigmod
tanh
ReLU
LeakyReLU
ReLU6
参考资料
|
为什么要用激活函数 |
在神经网络中，如果不对上一层结点的输出做非线性转换的话，再深的网络也是线性模型，只能把输入线性组合再输出（如下图），不能学习到复杂的映射关系，因此需要使用激活函数这个非线性函数做转换。
|
sigmod |
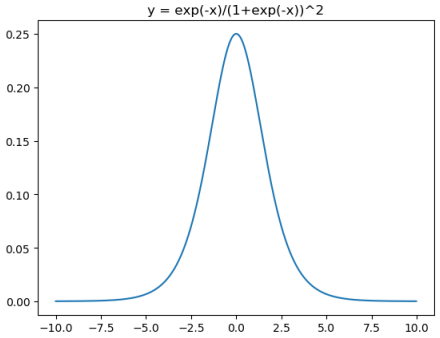
Sigmod激活函数和导函数分别为
对应的图像分别为：
对应代码为：
from matplotlib import pyplot as plt
import numpy as np
fig = plt.figure()
x = np.arange(-10, 10, 0.025)
plt.plot(x,1/(1+np.exp(-x)))
plt.title("y = 1/(1+exp(-x))")
plt.show()
plt.plot(x,np.exp(-x)/(1+np.exp(-x))**2)
plt.title("y = exp(-x)/(1+exp(-x))^2")
plt.show()
Sigmod(x)的缺点：
①输出范围在0~1之间，均值为0.5，需要做数据偏移，不方便下一层的学习。
②当x很小或很大时，存在导数很小的情况。另外，神经网络主要的训练方法是BP算法，BP算法的基础是导数的链式法则，也就是多个导数的乘积。而sigmoid的导数最大为0.25，多个小于等于0.25的数值相乘，其运算结果很小。随着神经网络层数的加深，梯度后向传播到浅层网络时，基本无法引起参数的扰动，也就是没有将loss的信息传递到浅层网络，这样网络就无法训练学习了。这就是所谓的梯度消失。
|
tanh |
tanh是双曲函数中的一个，tanh()为双曲正切。在数学中，双曲正切“tanh”是由双曲正弦和双曲余弦这两种基本双曲函数推导而来。
tanh激活函数和导函数分别为
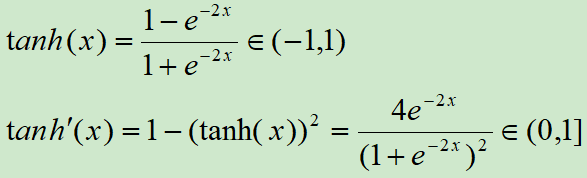
对应的图像分别为：
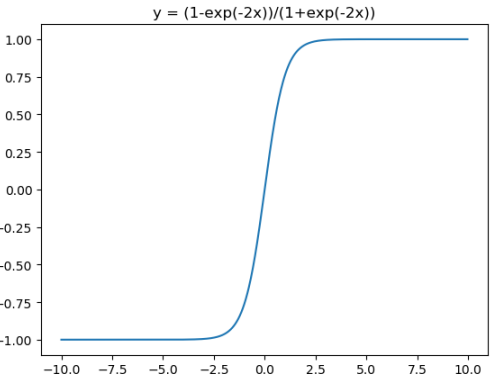
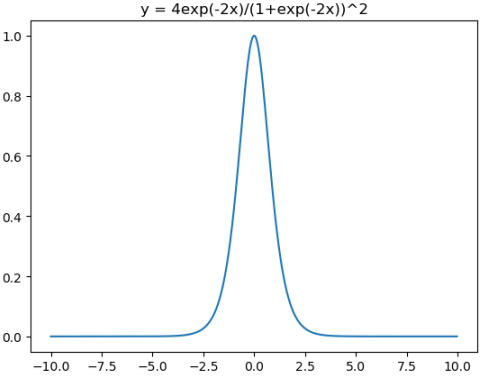
对应代码为：
from matplotlib import pyplot as plt
import numpy as np
fig = plt.figure()
x = np.arange(-10, 10, 0.025)
plt.plot(x,(1-np.exp(-2*x))/(1+np.exp(-2*x)))
plt.title("y = (1-exp(-2x))/(1+exp(-2x))")
plt.show()
plt.plot(x,4*np.exp(-2*x)/(1+np.exp(-2*x))**2)
plt.title("y = 4exp(-2x)/(1+exp(-2x))^2")
plt.show()
在神经网络的应用中，tanh通常要优于sigmod的，因为tanh的输出在-1~1之间，均值为0，更方便下一层网络的学习。但有一个例外，如果做二分类，输出层可以使用sigmod，因为他可以算出属于某一类的概率
Sigmod(x)和tanh(x)都有一个缺点：在深层网络的学习中容易出现梯度消失，造成学习无法进行。
|
ReLU |
针对sigmod和tanh的缺点，提出了ReLU函数
线性整流函数（Rectified Linear Unit, ReLU），又称修正线性单元，是一种人工神经网络中常用的激活函数（activation function），通常指代以斜坡函数及其变种为代表的非线性函数。
ReLU激活函数和导函数分别为
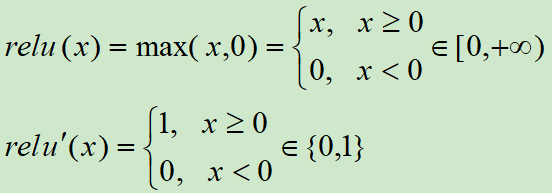
对应的图像分别为：
对应代码为：
from matplotlib import pyplot as plt
import numpy as np
fig = plt.figure()
x = np.arange(-10, 10, 0.025)
plt.plot(x,np.clip(x,0,10e30))
plt.title("y = relu(x)=max(x,0)")
plt.show()
from matplotlib import pyplot as plt
plt.plot(x,x>0,"o")
plt.title("y = relu'(x)")
plt.show()
Relu的一个缺点是当x为负时导数等于零，但是在实践中没有问题，也可以使用leaky Relu。
总的来说Relu是神经网络中非常常用的激活函数。
|
LeakyReLU |
Leaky ReLU激活函数和导函数分别为
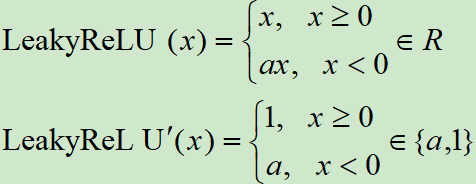
对应的图像分别为：
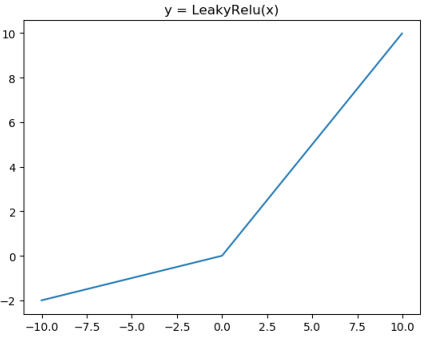
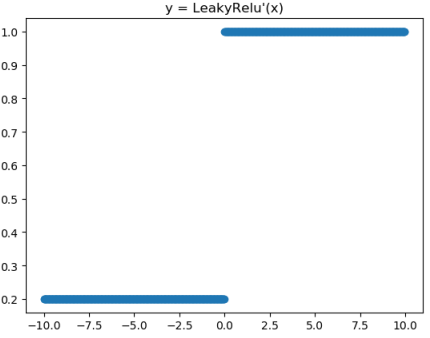
对应代码为：
from matplotlib import pyplot as plt import numpy as np fig = plt.figure() x = np.arange(-10, 10, 0.025) a = 0.2 plt.plot(x,x*np.clip((x>=0),a,1)) plt.title("y = LeakyRelu(x)") plt.show() from matplotlib import pyplot as plt plt.plot(x,np.clip((x>=0),a,1),"o") plt.title("y = LeakyRelu'(x)") plt.show()
|
ReLU6 |
Relu在x>0的区域使用x进行线性激活，有可能造成激活后的值太大，影响模型的稳定性，为抵消ReLU激励函数的线性增长部分，可以使用Relu6函数
ReLU激活函数和导函数分别为
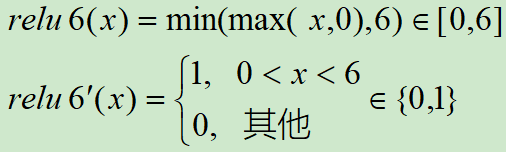
对应的图像分别为：
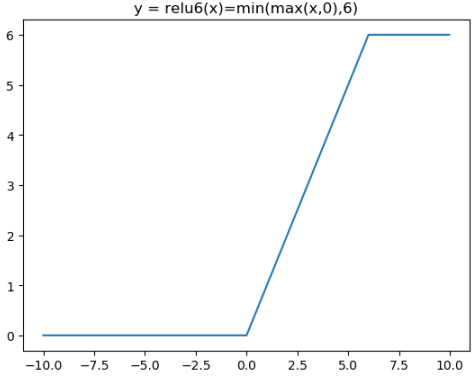
对应代码为：
from matplotlib import pyplot as plt import numpy as np fig = plt.figure() x = np.arange(-10, 10, 0.025) plt.plot(x,np.clip(x,0,6)) plt.title("y = relu6(x)=min(max(x,0),6)") plt.show() from matplotlib import pyplot as plt plt.plot(x,(x>0)&(x<6),"o") plt.title("y = relu6'(x)") plt.show()
|
参考资料 |
吴恩达深度学习
神经网络中的梯度消失
https://www.cnblogs.com/mengnan/p/9480804.html
《图解深度学习与神经网络：从张量到TensorFlow实现》_张平
