深度学习面试题04:随机梯度下降法、批量梯度下降法、小批量梯度下降
目录
一元线性回归模型
一元线性回归代价函数图像
梯度下降求解
SGD、BGD、Mini-batchGD的特点
参考资料
在《深度学习面试题03改进版梯度下降法Adagrad、RMSprop、Momentum、Adam》中讲到了多种改进的梯度下降公式。而这篇文章和03篇描述的不是一个事情,我们从一个例子说起,就知道改良的GD算法和本节介绍的GD算法的不同点了。
|
一元线性回归模型 |
举例:以房屋面积预测房屋价格
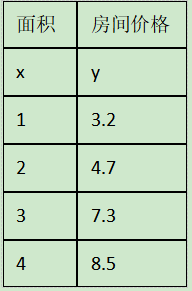
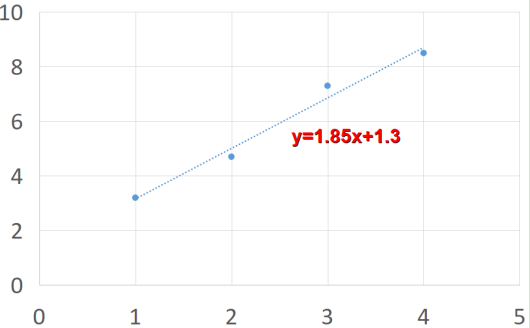
假设函数可以设置为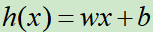
|
一元线性回归代价函数图像 |
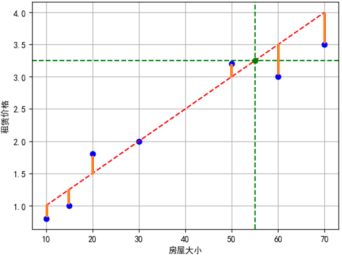
每一个预测值都与真实值存在一个差距,差距的平方和就可以作为一个代价函数。
因此代价函数为:
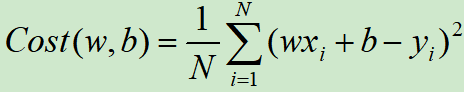
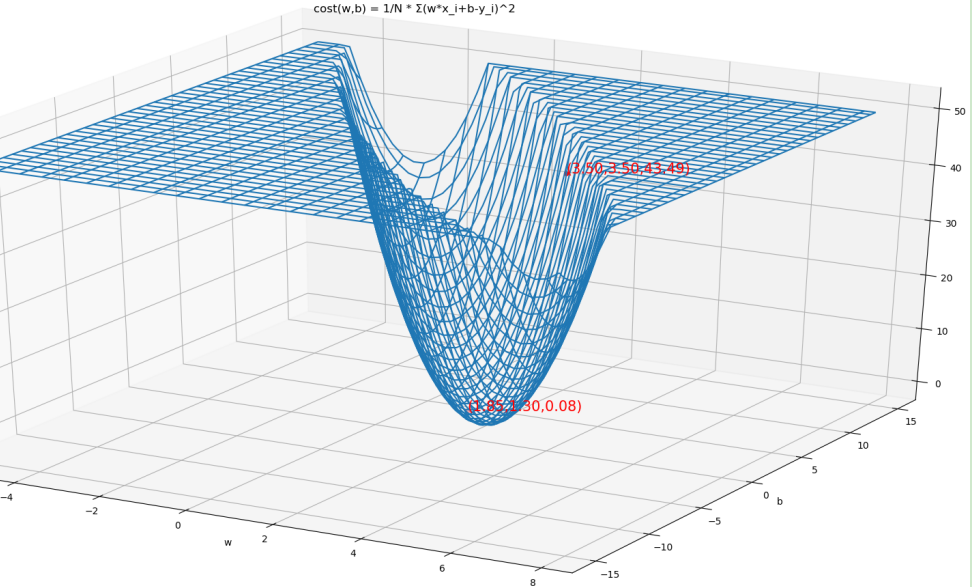
如下图所示(为方便观察,做了一个截断)

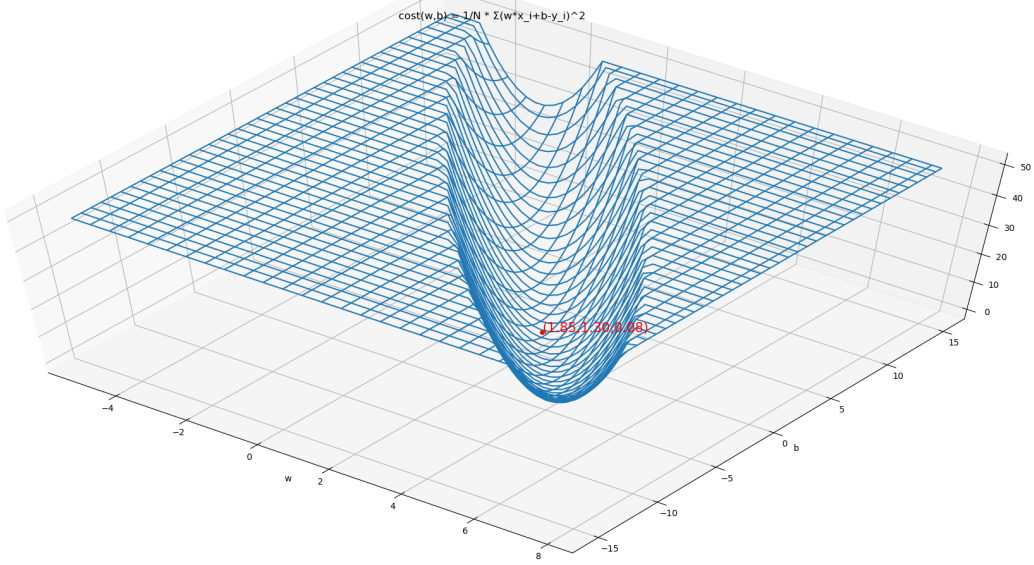
代码为:

from matplotlib import pyplot as plt import numpy as np from mpl_toolkits.mplot3d import Axes3D fig = plt.figure() ax = Axes3D(fig) w = np.arange(-5, 8, .25) b = np.arange(-15, 15, .25) x = np.array([1,2,3,4]) y = np.array([3.2,4.7,7.3,8.5]) w, b = np.meshgrid(w, b) R = 0 for i in range(len(x)): R += (w*x[i]+b-y[i])**2 R /= len(x) a = R<50 R = ~a*50+R*a # ax.plot_surface(w, b, R, rstride=1, cstride=1, cmap='rainbow', ) ax.plot_wireframe(w, b, R) plt.title("cost(w,b) = 1/N * Σ(w*x_i+b-y_i)^2") X = np.array([1.85,3.5]) # [ 0 3 6 9 12 15 18 21] Y = np.array([1.3,3.5]) # [ 1 4 7 10 13 16 19 22] R = 0 for i in range(len(x)): R += (X*x[i]+Y-y[i])**2 R /= len(x) Z = R ax.scatter(X, Y, Z, c='r', label='顺序点') for i in range(len(X)): ax.text(X[i], Y[i], Z[i], "({:.2f},{:.2f},{:.2f})".format(X[i], Y[i], Z[i]), color='red',fontsize=15) plt.xlabel("w") plt.ylabel("b") plt.show()
|
梯度下降求解 |
当使用梯度下降法求解时,假设初始化(w,b)=(3.5,3.5)
代价函数关于w和b的偏导数为:
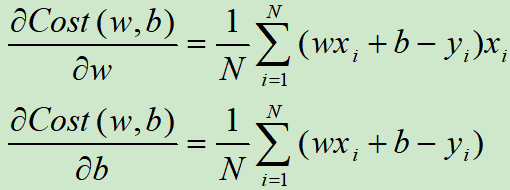
重点来了:Adagrad、RMSprop、Adam等算法都是建立在偏导数之上的,他们并不关心上式中N的取值,N取1,取100,还是取N,Adagrad、RMSprop、Adam等算法都可以运行。
而随机梯度下降法(Stochastic Gradient Descent,SGD),批量梯度下降法(Batch Gradient Descent,BGD),小批量梯度下降法(Mini-batch Gradient Descent,Mini-batchGD)则是研究这里的N的大小的。
如果N=1,此时为SGD,计算代价函数梯度的时候只考虑一个样本;
如果N=样本容量,此时为BGD,计算代价函数梯度的时候考虑全部样本;
如果N=m,1<m<N,此时为Mini-batchGD,计算代价函数梯度的时候考虑一小批样本。
|
SGD、BGD、Mini-batchGD的特点 |
SGD计算根据随机一个样本构造出来的代价函数的梯度,这与计算根据全部样本构造出来的代价函数的梯度肯定有偏差,也许是一个不好的梯度方向,下降时候并不沿着最有的方向下降,但是优点是可以快速的计算一个近似梯度,因为计算量缩减到原来的1/N。
BGD计算根据全部样本的构造出来的代价函数的梯度,方向肯定是沿着当前最优的下降方向,但是计算代价较高,当数据集较大时,相当耗时。
Mini-batchGD就不用说了,是前两者的折中
下面用图像演示一下BGD和SGD下降的过程
BGD效果如下
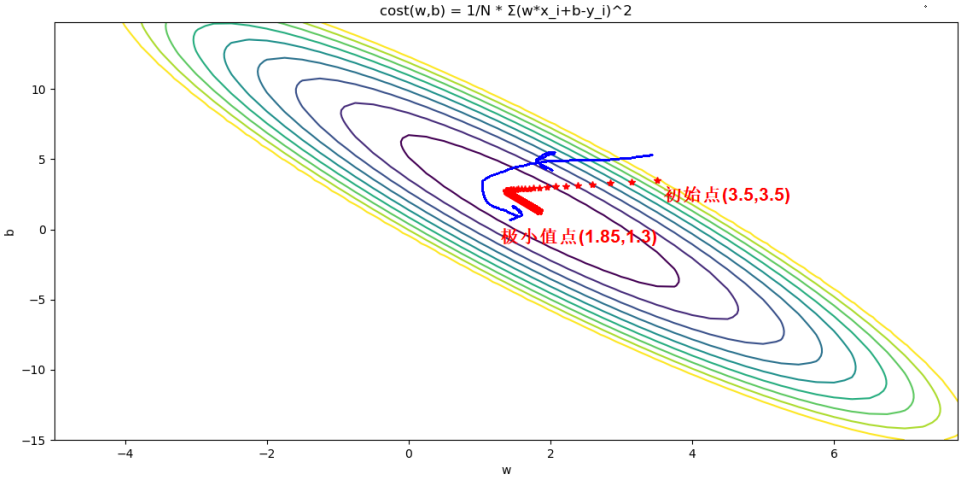
BGD代码如下:

from matplotlib import pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
w = np.arange(-5, 8, .25)
b = np.arange(-15, 15, .25)
x = np.array([1,2,3,4])
y = np.array([3.2,4.7,7.3,8.5])
w, b = np.meshgrid(w, b)
R = 0
for i in range(len(x)):
R += (w*x[i]+b-y[i])**2
R /= len(x)
a = R<50
R = ~a*50+R*a
ax = plt.subplot()
plt.contour(w, b, R,10)
plt.title("cost(w,b) = 1/N * Σ(w*x_i+b-y_i)^2")
w = 3.5
b = 3.5
W = []
B = []
for i in range(2000):
W.append(w)
B.append(b)
w -= 0.02*1/len(x)*sum((w*x+b-y)*x)
b -= 0.02*1/len(x)*sum((w*x+b-y))
print(w,b)
plt.plot(W,B,"r*")
plt.xlabel("w")
plt.ylabel("b")
plt.show()
SGD效果如下:
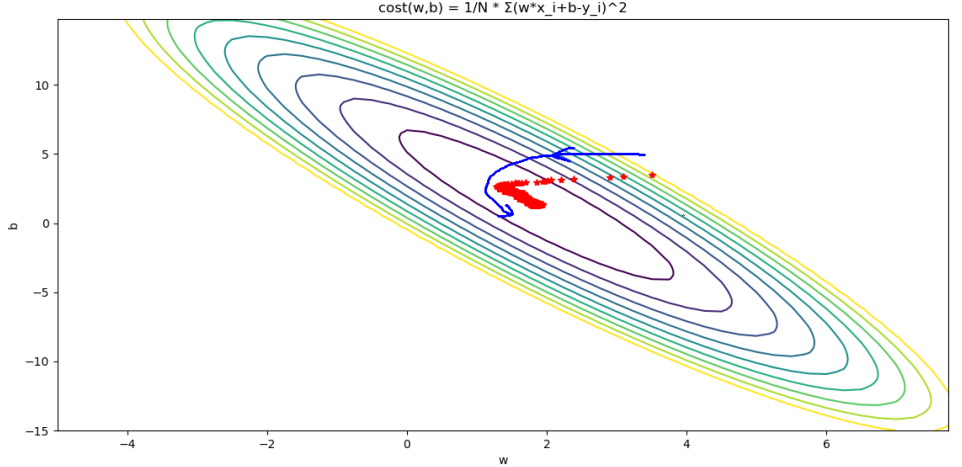
很明显SGD在下降过程中存在方向不稳定的情况,但是最终还是能收敛到最优点
SGD代码如下:

from matplotlib import pyplot as plt import numpy as np from mpl_toolkits.mplot3d import Axes3D import random fig = plt.figure() w = np.arange(-5, 8, .25) b = np.arange(-15, 15, .25) x = np.array([1,2,3,4]) y = np.array([3.2,4.7,7.3,8.5]) w, b = np.meshgrid(w, b) R = 0 for i in range(len(x)): R += (w*x[i]+b-y[i])**2 R /= len(x) a = R<50 R = ~a*50+R*a ax = plt.subplot() plt.contour(w, b, R,10) plt.title("cost(w,b) = 1/N * Σ(w*x_i+b-y_i)^2") w = 3.5 b = 3.5 W = [] B = [] for i in range(2000): W.append(w) B.append(b) p = random.randint(0, len(x)-1) w -= 0.02*(w*x[p]+b-y[p])*x[p] b -= 0.02*(w*x[p]+b-y[p]) print(w,b) plt.plot(W,B,"r*") plt.xlabel("w") plt.ylabel("b") plt.show()
|
参考资料 |
《图解深度学习与神经网络:从张量到TensorFlow实现》_张平





