图的深度优先遍历和广度优先遍历
1.图的表示
图一般有两种表示方式:一是用二维数组表示(邻接矩阵),而是用数组加链表表示(邻接表)
邻接矩阵:将所有结点从0-n标记好索引,分别作为二维数组的横向索引和纵向索引,如果图中两个节点直接相连,则两个结点索引对应的坐标元素设为1,否则为0,如图:
这种表示方式的优点是简单,便于后面的计算和遍历,缺点是空间浪费
邻接表:一个长度为结点个数的数组,数组每个元素都是一个链表,记录了当前数组元素索引对应的结点直接连接的结点索引,如图:
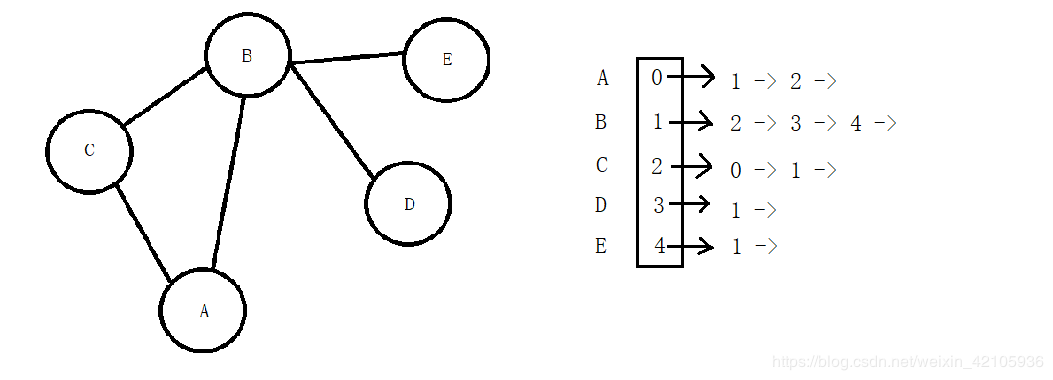
2.图的深度优先遍历(Depth First Search)和广度优先遍历(Broad First Search)
深度优先遍历:
选择一个结点作为第一个结点,从这个结点出发,访问与之相邻的第二个结点,如果第二个节点有相邻结点,那么继续向第二个结点的相邻结点访问,直到遇到某个结点没有未被访问过的邻结点时,回退到前一个访问的节点,继续访问前一个节点的其他未被访问过的相邻结点,然后继续向前访问。
如果按照上面的图,则访问步骤可以如下:
1.访问第一个节点:A
2.一直往后遍历,直到C没有未被访问过的相邻结点:A->B->C
3.回退到B,继续从B开始访问其他未被访问过的相邻结点D:A->B->C->D
4.依次类推,回退到B继续访问E:A->B->C->D->E
代码如下:
public void dfs(int i) {
System.out.print(vertexList.get(i) + "->");
isSearched[i] = true;
for (int j = 0; j < edges.length; j++) {//一个结点访问之后,从5个结点找到接下来要访问的结点
if (edges[i][j] > 0 && !isSearched[j]) {//接下来要访问的结点必须满足:1.与当前结点i要相连;2.未被访问过
dfs(j);//找到下一个结点以后,继续以下一个结点作为当前结点来进行递归遍历
}
}
}
广度优先遍历:
1.选择一个结点作为初始结点,将初始结点的所有未被访问过的相邻结点访问一遍,过程中记录邻接点的访问顺序,如v1,v2...vn;
2.按照访问结点顺序,依次再以每个邻接点作为当前结点访问其所有的未被访问的相邻接点,并记录邻接点顺序,如v1访问邻接点v11,v12...v1n,接着访问v2的邻接点v21,v22...v2n;
3.当v1-v2的所有邻接点访问完之后,v11-v1n按照步骤2,依次类推,直到所有节点访问结束
这里的难点是如何记录这些结点的访问顺序,可以使用一个队列Queue,先将第一个结点索引入列,每次访问队列中的第一个元素,再将该元素对应的结点的所有邻接点索引入队列,然后从队列中将第一个元素出列,以此类推...
代码实现如下:
public void bfs(int i) {
queue.addLast(i);//将第一个结点的索引记录到队列中
while(!queue.isEmpty){
bfs_search(queue.getFirst());//访问队列中的头元素
queue.removeFirst();
}
}
public void bfs_search(int i) {
//加上这个判断的原因:上一个结点将邻接节点索引放入队列之后,下一个邻接结点有可能会将相同的邻接节点入队列
//例如:A的邻接结点BC,入队列后queue为C->B->A,后面轮到B时,B的邻接结点为CDE,即队列可能变为D->C->C->B
if(!isSearched[i]){
System.out.print(vertexList.get(i) + "->");
isSearched[i] = true;
}
//遍历第一个结点的邻接节点
for (int j = 0; j < edges.length; j++) {
if (edges[i][j] > 0 && !isSearched[j]) {
queue.addLast(j);
}
}
}
图的完整代码如下:
/**
* created by it_hushuai
* 2020/2/29 21:50
*/
public class Graph {
private ArrayList<String> vertexList;//存储顶点集合
private int[][] edges;//存储图对应的邻结矩阵
private int numOfEdges;//表示边的数目
private boolean[] isSearched;//记录结点是否被访问
private LinkedList<Integer> queue = new LinkedList<>();//广度优先中记录节点顺序
public Graph(int n) {
edges = new int[n][n];
vertexList = new ArrayList<>(n);
isSearched = new boolean[n];
}
/**
* 返回节点的个数
*
* @return
*/
public int getNumOfVertex() {
return vertexList.size();
}
/**
* 返回边的数目
*
* @return
*/
public int getNumOfEdges() {
return numOfEdges;
}
/**
* 返回节点下标对应的数据
*
* @param i
* @return
*/
public String getValueByIndex(int i) {
return vertexList.get(i);
}
/**
* 返回两个节点之间的权值
*
* @param i1
* @param i2
* @return
*/
public int getWeight(int i1, int i2) {
return edges[i1][i2];
}
/**
* 插入节点
*
* @param vertex
*/
public void insertVertex(String vertex) {
vertexList.add(vertex);
}
/**
* 添加边,也就是确定两个节点之间的关系
*
* @param i1
* @param i2
* @param weight
*/
public void addEdges(int i1, int i2, int weight) {
edges[i1][i2] = weight;
edges[i2][i1] = weight;
numOfEdges++;
}
/**
* 显示图对应的邻结矩阵
*/
public void showGraph() {
for (int[] edge : edges) {
System.out.println(Arrays.toString(edge));
}
}
/**
* 图的深度优先遍历
*
* @param i
*/
public void dfs(int i) {
System.out.print(vertexList.get(i) + "->");
isSearched[i] = true;
for (int j = 0; j < edges.length; j++) {//一个结点遍历之后,从5个结点找到接下来要遍历的结点
if (edges[i][j] > 0 && !isSearched[j]) {//接下来要出现的结点必须满足:1.与当前节点i要相连;2.未被遍历过
dfs(j);//找到下一个节点以后,继续以下一个节点作为当前节点来进行递归遍历
}
}
}
/**
* 图的广度优先遍历
*
* @param i
*/
public void bfs(int i) {
queue.addLast(i);//将第一个结点的索引记录到队列中
while (!queue.isEmpty()) {
bfs_search(queue.getFirst());
queue.removeFirst();
}
}
public void bfs_search(int i) {
//加上这个判断的原因:上一个结点将邻接节点索引放入队列之后,下一个邻接结点有可能会将相同的邻接节点入队列
//例如:A的邻接结点BC,入队列后queue为C->B->A,后面轮到B时,B的邻接结点为CDE,即队列可能变为D->C->C->B
if(!isSearched[i]){
System.out.print(vertexList.get(i) + "->");
isSearched[i] = true;
}
//遍历第一个结点的邻接节点
for (int j = 0; j < edges.length; j++) {
if (edges[i][j] > 0 && !isSearched[j]) {
queue.addLast(j);
}
}
}
public static void main(String[] args) {
Graph graph = new Graph(5);
graph.insertVertex("A");
graph.insertVertex("B");
graph.insertVertex("C");
graph.insertVertex("D");
graph.insertVertex("E");
graph.addEdges(0, 1, 1);
graph.addEdges(0, 2, 1);
graph.addEdges(1, 3, 1);
graph.addEdges(1, 4, 1);
graph.addEdges(1, 2, 1);
graph.showGraph();
// graph.dfs(0);
graph.bfs(0);
}
}

