float32和float64

float32 和 float64#

Go语言中提供了两种精度的浮点数 float32 和 float64。

float32，也即我们常说的单精度，存储占用4个字节，也即4*8=32位，其中1位用来符号，8位用来指数，剩下的23位表示尾数

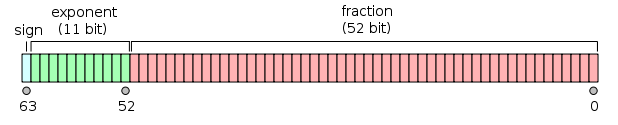
float64，也即我们熟悉的双精度，存储占用8个字节，也即8*8=64位，其中1位用来符号，11位用来指数，剩下的52位表示尾数

那么精度是什么意思？有效位有多少位？

 

 

精度主要取决于尾数部分的位数。

对于 float32（单精度）来说，表示尾数的为23位，除去全部为0的情况以外，最小为2^{-23，约等于1.19*10}-7，所以float小数部分只能精确到后面6位，加上小数点前的一位，即有效数字为7位。

同理 float64（单精度）的尾数部分为 52位，最小为2^{-52，约为2.22*10}-16，所以精确到小数点后15位，加上小数点前的一位，有效位数为16位。

 

 

通过以上，可以总结出以下几点：

一、float32 和 float64 可以表示的数值很多

浮点数类型的取值范围可以从很微小到很巨大。浮点数取值范围的极限值可以在 math 包中找到：

• 常量 math.MaxFloat32 表示 float32 能取到的最大数值，大约是 3.4e38；
• 常量 math.MaxFloat64 表示 float64 能取到的最大数值，大约是 1.8e308；
• float32 和 float64 能表示的最小值分别为 1.4e-45 和 4.9e-324。

二、数值很大但精度有限

人家虽然能表示的数值很大，但精度位却没有那么大。

• float32的精度只能提供大约6个十进制数（表示后科学计数法后，小数点后6位）的精度
• float64的精度能提供大约15个十进制数（表示后科学计数法后，小数点后15位）的精度

这里的精度是什么意思呢？

比如 10000018这个数，用 float32 的类型来表示的话，由于其有效位是7位，将10000018 表示成科学计数法，就是 1.0000018 * 10^7，能精确到小数点后面6位。

此时用科学计数法表示后，小数点后有7位，刚刚满足我们的精度要求，意思是什么呢？此时你对这个数进行+1或者-1等数学运算，都能保证计算结果是精确的

import "fmt"

var myfloat float32 = 10000018
func main() {
  fmt.Println("myfloat: ", myfloat)
  fmt.Println("myfloat: ", myfloat+1)
}
/*
myfloat: 1.0000018e+07
myfloat: 1.0000019e+07
/

　　

上面举了一个刚好满足精度要求数据的临界情况，为了做对比，下面也举一个刚好不满足精度要求的例子。只要给这个数值多加一位数就行了。

换成 100000187，同样使用 float32类型，表示成科学计数法，由于精度有限，表示的时候小数点后面7位是准确的，但若是对其进行数学运算，由于第八位无法表示，所以运算后第七位的值，就会变得不精确。

这里我们写个代码来验证一下，按照我们的理解下面 myfloat01 = 100000182 ，对其+5 操作后，应该等于 myfloat02 = 100000187，

import "fmt"

var myfloat01 float32 = 100000182
var myfloat02 float32 = 100000187
func main() {
    fmt.Println("myfloat: ", myfloat01)
    fmt.Println("myfloat: ", myfloat01+5)
    fmt.Println(myfloat02 == myfloat01+5)
}

　　

但是由于其类型是 float32，精度不足，导致最后比较的结果是不相等（从小数点后第七位开始不精确）

myfloat: 1.00000184e+08
myfloat: 1.0000019e+08
false

由于精度的问题，就会出现这种很怪异的现象，myfloat == myfloat +1 会返回 true 。

转载 ：https://www.cnblogs.com/HappyTeemo/p/15405577.html