计算几何
前置知识
向量 和 三角函数
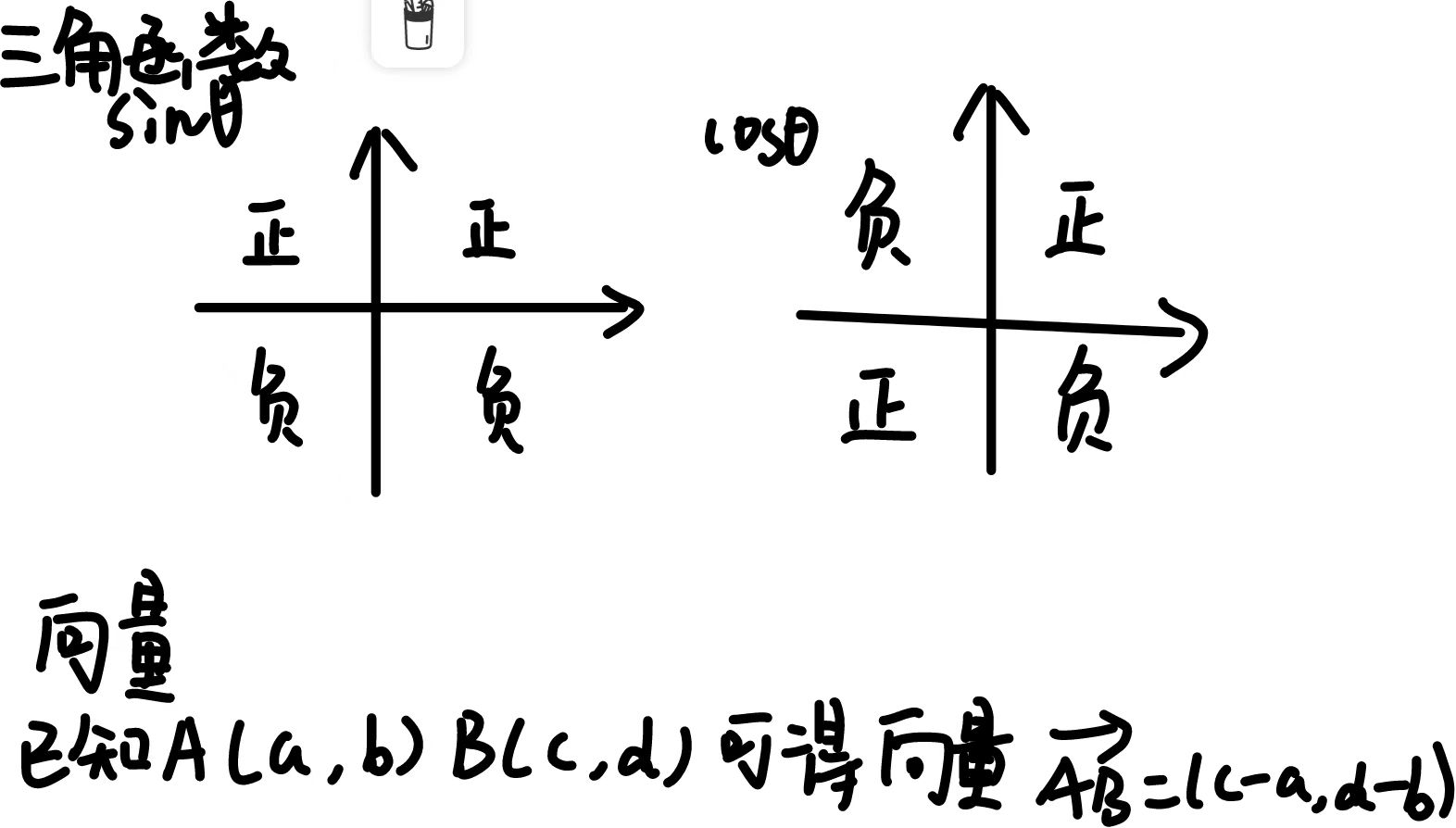
点积

Code:
struct Point {
double x, y;
} ;
double dot (Point a, Point b) {
return a.x * b.x + a.y * b.y;
}
double len (Point a) {
return sqrt((a.x * a.x + a.y * a.y));
}
double angle (Point a, Point b) {
return dot(a, b) / len(a) / len(b);
}
叉积

struct Point {
int x, y;
} ;
int cross (Point a, Point b) { // 以原点
return (a.x * b.y - a.y * b.x);
}
int cross (Point a, Point b, Point c) {
return (b.x - a.x) * (c.y - a.y) - (b.y - a.y) * (c.x - a.x);
}
/*
cross(a, b, c) > 0 c 在 ab 的左侧
cross(a, b, c) = 0 a, b, c三点共线
cross(a, b, c) < 0 c 在 ab的右侧
*/
解释
cross(a, b, c) > 0 c 在 ab 的左侧 cross(a, b, c) = 0 a, b, c三点共线 cross(a, b, c) < 0 c 在 ab的右侧
举个例子
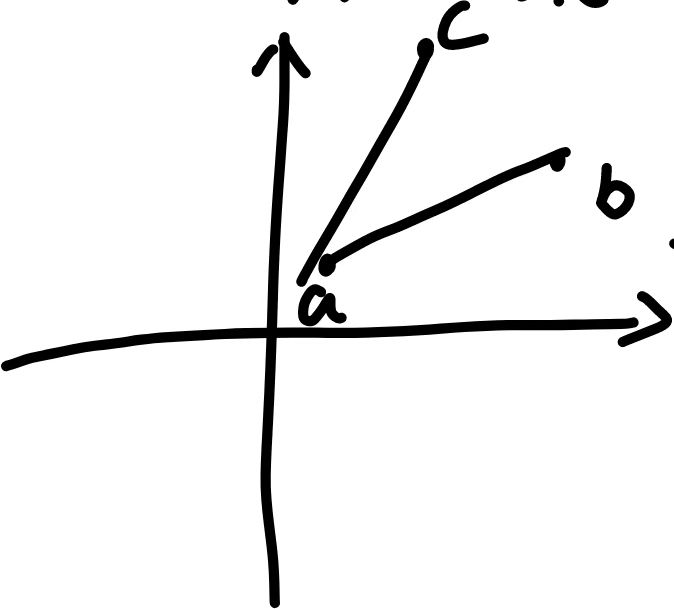
对于这三个点其实求的是向量ab, 和 向量ac的叉积, 不难得出 对于ab 或者ac的长度必然是正数, 其实就是cos(x)的转化, 如果cos(x) > 0也就说明了c在ab的左侧, 可以从图中得到, 如果 = 0其实就是三点共线, cos(x) < 0就是c在ab的右侧 了解到这个性质我们就可以看一下下面这题 Transmitters
A - Transmitters
题意:
给你一个点的坐标和半径, 然后给平面上的点集S, 求以这个点为圆心的半圆最多能覆盖S中的点的个数
思路:
1.切入点1, 如果以这个点为圆心的半圆要求能覆盖, 必然需要满足点到圆心的距离需要小于等于半径
2.切入点2,需要以这个点作半圆最多能覆盖S, 那么我们可以得到, 圆心和枚举的一个点作为半径化圆必然得到最优且得到的圆利用叉积的知识必然是ac在ab的左侧 这里ab的向量指的是
圆心和枚举的一个点, ac只的枚举整个区间的向量, 那么可以得到如果需要满足条件 ac一定要满足>=0 也就意味着ac在ab的左侧
解释:
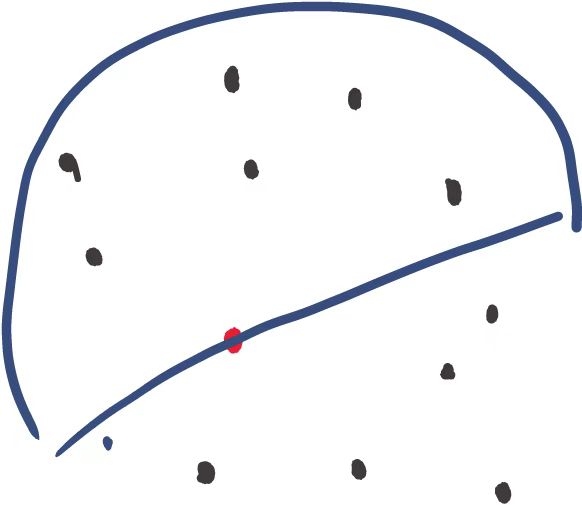
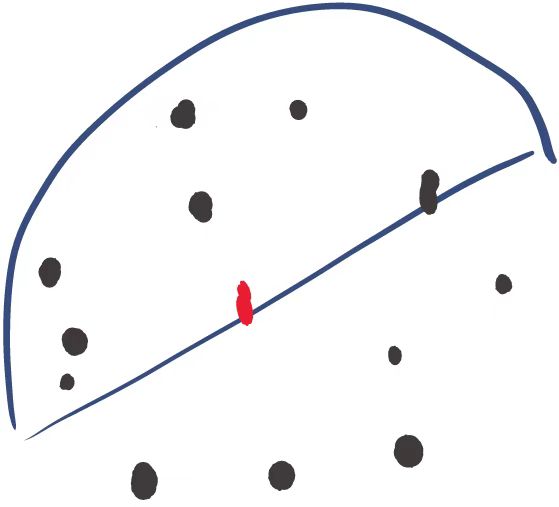
第一张图代表着随机刷新点位与圆心形成半圆, 和以已经存在且能被覆盖的点位画圆明显发现扫描的空间需要更大, 那么圆心和枚举的一个点作为半径化圆必然得到最优
复杂度:
O(n ^ 2)
Code:
//https://github.com/Ckeyliuhi/acm-iters
#include <iostream>
#include <cmath>
using namespace std;
const int N = 2e2 + 5;
struct Point {
int x, y;
} P[N], Cir, Die;
int n, cnt = 0;
double r;
double cross (Point a, Point b, Point c) {
return (b.x - a.x) * (c.y - a.y) - (b.y - a.y) * (c.x - a.x);
}
/*
cross(a, b, c) > 0 c 在 ab 的左侧
cross(a, b, c) = 0 a, b, c三点共线
cross(a, b, c) < 0 c 在 ab的右侧
*/
bool check (Point a, Point b) {
return double((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y)) <= r * r;
}
void solve() {
while (cin >> Cir.x >> Cir.y >> r, r >= 0) {
cin >> n; cnt = 0;
for (int i = 1; i <= n; i++) {
cin >> Die.x >> Die.y;
if (check (Cir, Die)) P[++cnt] = Die;
}
int ans = 0;
for (int i = 1; i <= cnt; i++) {
int rec = 0;
for (int j = 1; j <= cnt; j++) {
if (cross(Cir, P[i], P[j]) >= 0) rec++;
}
ans = max(ans, rec);
}
cout << ans << '\n';
}
}
int main() {
cin.tie(0) -> sync_with_stdio(false);
int t = 1;
// cin >> t;
while (t--) {
solve();
}
return 0;
}
B - TOYS
题意:
有一个长方形盒子,有n个板隔开,分成n+1个区域,又给了m个玩具的坐标,问你每个区域内的玩具有几个
看图:

思路:
切入点1 假设硬纸板隔板不会相交,并且按照从左到右的顺序排序, 这是题目中提到的, 我们可以发现它是存在单调性的, 对于每一个玩具, 我们可以通过二分来实现我们区间查找
(如何二分) 利用叉积的知识
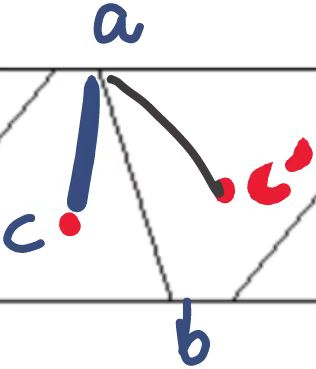
通过观察该图像 我们假设存在两个点分别是c' c我们可以发现当向量ac在向量ab的左侧的时候我们玩具的区域是在左边, 同理, ac'在ab的右侧也就意味着玩具的区域是在右边, 通过二分的方式在区间 [0, n] 上寻找答案。接下来通过计算每对相邻点的叉积值来判断其相对位置。(套一个二分板子即可)
复杂度:
O(nlogn)
Code:
//https://github.com/Ckeyliuhi/acm-iters
#include <iostream>
using namespace std;
const int N = 5e3 + 5;
typedef long long LL;
struct Point {
LL x, y;
} P[N], P2[N], Die;
int n;
LL ans[N];
LL cross (Point a, Point b, Point c) {
return (b.x - a.x) * (c.y - a.y) - (b.y - a.y) * (c.x - a.x);
}
int check (Point a) {
int l = 0, r = n, res;
while (l <= r) {
int mid = (l + r) >> 1;
if (cross(P2[mid], P[mid], a) <= 0) {
l = mid + 1;
res = mid;
} else {
r = mid - 1;
}
}
return res;
}
void solve() {
bool ok = 1;
while (cin >> n, n) {
int m; LL x1, y1, x2, y2;
cin >> m >> x1 >> y1 >> x2 >> y2;
P[0].x = x1, P[0].y = y1, P2[0].x = x1, P2[0].y = y2;
for (int i = 1; i <= n; i++) {
LL xi, xi2;
cin >> xi >> xi2;
P[i].x = xi, P[i].y = y1, P2[i].x = xi2, P2[i].y = y2;
}
for ( ; m--; ) {
cin >> Die.x >> Die.y;
ans[check(Die)] ++;
}
if (ok) {
ok = 0;
} else {
cout << '\n';
}
for (int i = 0; i <= n; i++) {
cout << i << ':' << ' ' << ans[i] << '\n';
}
for (int i = 0; i <= n; i++) {
ans[i] = 0;
}
}
}
int main() {
cin.tie(0) -> sync_with_stdio(false);
int t = 1;
// cin >> t;
while (t--) {
solve();
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号