七大排序算法

• 冒选插桶快归堆，以下均为升序

1 冒泡排序

• 描述：

  • 比较相邻的元素。如果第一个比第二个大，就交换它们两个；
  • 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对，这样在最后的元素应该会是最大的数；
  • 针对所有的元素重复以上的步骤，除了最后一个；
  • 重复步骤1~3，直到排序完成。

   public int[] sortArray1(int[] nums) {
       int n = nums.length;
       for(int i = n - 1;i>=0;i--){
           for(int j = 0;j<i;j++){
               if(nums[j] > nums[j+1]){
                   swap(nums,j,j+1);
               }
           }
       }
       return nums;
   }
  
  void swap(int[] nums,int i,int j){
      int temp = nums[i];
      nums[i] = nums[j];
      nums[j] = temp;
  }
  

2 选择排序

• 在要排序的一组数中，选出最小的一个数与第一个位置的数交换；然后在剩下的数当中再找最小的与第二个位置的数交换，如此循环到倒数第二个数和最后一个数比较为止。

  public int[] sortArray2(int[] nums) {
      int n = nums.length;
      for(int i = 0;i<n;i++){
          int min = i;
          for(int j = i+1;j<n;j++){
              if(nums[min] > nums[j]){
                  min = j;
              }
          }
          swap(nums,i,min);
      }
      return nums;
  }
  

3 插入排序

• 一次插一个，插一个排一次

   public int[] sortArray3(int[] nums) {
       int n = nums.length;
       for(int i = 1;i<n;i++){
           int temp = nums[i];
           int j = i-1;
           for(;j>=0 && temp <= nums[j];j--){  // 注意这边是temp，不是nums[i]
               nums[j+1] = nums[j];
           }          
           nums[j+1] = temp;
       }
       return nums;
   }
  

4 计数排序

计数排序算法的原理如下：

1.找出待排序的数组中最大和最小的元素；

2.统计数组中每个值为i的元素出现的次数，存入数组C的第i项；

3.对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）；

4.反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1。

5 快速排序

• 选择一个基准元素,通常选择第一个元素或者最后一个元素,通过一趟扫描，将待排序列分成两部分,一部分比基准元素小,一部分大于等于基准元素,此时基准元素在其排好序后的正确位置,然后再用同样的方法递归地排序划分的两部分。

  public void quick(int[] nums, int low, int high) {
      if (low < high) {
          int middle = getMiddle(nums, low, high);// 将数组进行一分为二
          quick(nums, low, middle - 1); // 对低字表进行递归排序
          quick(nums, middle + 1, high);// 对高字表进行递归排序
      }
  }
  
  private int getMiddle(int[] nums, int low, int high) {
      int tmp = nums[low]; // 数组的第一个作为中轴
      while (low < high) {
          while (low < high && nums[high] >= tmp) {
              high--;
          }
          nums[low] = nums[high]; // 比中轴小的记录移到低端
          while (low < high && nums[low] <= tmp) {
              low++;
          }
          nums[high] = nums[low]; // 比中轴大的记录移到高端
      }
      nums[low] = tmp; // 中轴记录到尾
      return low; // 返回中轴的位置
  }
  

6 归并排序

• 归并（Merge）排序法是将两个（或两个以上）有序表合并成一个新的有序表，即把待排序序列分为若干个子序列，每个子序列是有序的。然后再把有序子序列合并为整体有序序列。自上而下的递归。

  public void mergeSort(int[] nums,int left,int right){
      if(left<right){  
          //找出中间索引  
          int center=(left+right)/2;  
          //对左边数组进行递归  
          mergeSort(nums,left,center);  
          //对右边数组进行递归  
          mergeSort(nums,center+1,right);  
          //合并  
          merge(nums,left,center,right);  
      }  
  }
  
  private void merge(int[] nums, int left, int center, int right) {
      int [] tmpArr=new int[nums.length];  
      int mid=center+1;  
      //third记录中间数组的索引  
      int third=left;  
      int tmp=left;  
      while(left<=center&&mid<=right){  
          //从两个数组中取出最小的放入中间数组  
          if(nums[left]<=nums[mid]){  
              tmpArr[third++]=nums[left++];  
          }else{  
              tmpArr[third++]=nums[mid++];  
          }  
      }  
      //剩余部分依次放入中间数组  
      while(mid<=right){  
          tmpArr[third++]=nums[mid++];  
      }  
      while(left<=center){  
          tmpArr[third++]=nums[left++];  
      }  
      //将中间数组中的内容复制回原数组  
      while(tmp<=right){  
          nums[tmp]=tmpArr[tmp++];  
      }  
  }
  

  

7 堆排序

public int[] sortArray(int[] nums) {
    int n = nums.length;
    // 构建大根堆
    for(int i = n / 2 - 1;i>=0;i--){
        adjustHeap(nums,i,n);
    }
	
    // 将顶端的数与末尾的数交换，此时，末尾的数为最大值，剩余待排序数组个数为n-1
    // 将剩余的n-1个数再构造成大根堆，再将顶端数与n-1位置的数交换，如此反复执行，便能得到有序数组
    for(int i = n-1;i>=0;i--){
        swap(nums,0,i);
        adjustHeap(nums,0,i);
    }
    return nums;
}

// 小于length，将i位置的数向下调整
void adjustHeap(int[] nums,int i,int length){ 
    int temp = nums[i];
    for(int k = 2 * i +1;k<length;k=2*k+1){
        if(k+1<length && nums[k] < nums[k+1]) k++;
        if(nums[k] > temp){
            nums[i] = nums[k];
            i = k;
        }else{
            break;
        }
    }
    nums[i] = temp;
}

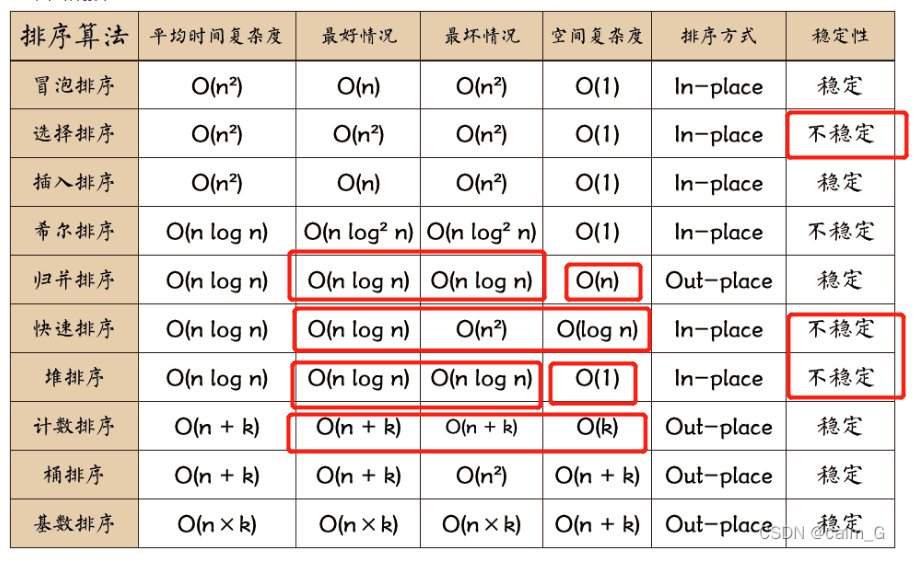
排序复杂度与稳定性