不平衡分类学习方法 --Imbalaced_learn
最近在进行一个产品推荐课题时,由于产品的特性导致正负样本严重失衡,远远大于3:1的比例(个人认为3:1是建模时正负样本的一个临界点),这样的样本不适合直接用来建模,例如正负样本的比例达到了50:1,就算算法全部预测为另一样本,准确率也会达到51/50=98%.具有很大的局限性.
处理不平衡样本的方法
解决方法主要分为两个方面。
- 第一种方案主要从数据的角度出发,主要方法为抽样,既然我们的样本是不平衡的,那么可以通过某种策略进行抽样,从而让我们的数据相对均衡一些;
- 第二种方案从算法的角度出发, 考虑不同误分类情况代价的差异性对算法进行优化,使得我们的算法在不平衡数据下也能有较好的效果。
这里我们主要从数据的角度进行讨论--采样技术
1.随机采样
随机采样技术是最直接,最简单易理解的处理方式,顾名思义,就是从已有样本中进行抽样,随机采样主要分为两种:(1)随机欠采样,(2)随机过采样.
随机欠采样就是从样本数量的多的类别S1中选择随机少量样本在和原有的少量样本合成作为新的数量级,使得两个样本的比例大致相同;
类似的,过采样就是从样本少的类别中多次采样少数类,采样的数量要大于原来的少数类的数量.随机过采样又分为有放回过采样和无放回过采样,这个和概率学上抽样是一个含义.
很明显,随机采样通过随机选取一些样本来改变样本分类分布的比例,这种方法比较简单,但是也存在诸多问题.
(1).欠采样技术:随机选取一部分数据,会导致数据的信息缺失,无法保证未被采样的数据不具有重要特征
(2).过采样技术:随机的扩大的了数据集,但是可能(极大的可能)会导致过拟合现象.
<<Python实现>>
Python有一个强大的处理不平衡数据的包--imblearn,该包依赖sklearn(>=0.19),numpy,six等相关包,可以通过pip install 进行安装.
实现随机欠采样:imblearn.under_sampling.RandomUnderSampler(ratio='auto', return_indices=False, random_state=None, replacement=False)
随机过采样:imlearn.over_sampling.RandomOverSampler(ratio='auto',random_state=None)
例子:
from collections import Counter from sklearn.datasets import make_classification ###生成不平衡样本,比例9:1 X,y=make_classification(n_classes=2,class_sep=2,weights=[0.1,0.9],n_informative=3,n_redundant=1,flip_y=0,n_features=20,n_clusters_per_class=1, n_samples=1000,random_state=10) print("original dataset shape {}".format(Counter(y))) >>original dataset shape Counter({1: 900, 0: 100}) ###随机欠采样 from imblearn.under_sampling import RandomUnderSampler rus=RandomUnderSampler(random_state=42) X_res,y_res=rus.fit_sample(X,y) print('Under Resampled dataset shape {}'.format(Counter(y_res))) >>Under Resampled dataset shape Counter({0: 100, 1: 100}) ##随机过采样 from imblearn.over_sampling import RandomOverSampler ros=RandomOverSampler(random_state=42) X_res,y_res=ros.fit_sample(X,y) print('Over Resampled dataset shape {}'.format(Counter(y_res))) >>Over Resampled dataset shape Counter({0: 900, 1: 900})
2.SMOTE算法
SMOTE算法又称为合成少数类过采样方法,SMOTE算法的基本思想是对少数类样本进行分 析并根据少数类样本人工合成新样本添加到数据集中,从而改进了随机过采样技术造成的过拟合问题.
算法流程:
- 对于少数类中每一个样本x,以欧氏距离为标准计算它到少数类样本集Sm中所有样本的距离,得到其k近邻。
- 根据样本不平衡比例设置一个采样比例以确定采样倍率N,对于每一个少数类样本x,从其k近邻中随机选择若干个样本,假设选择的近邻为x^。
- 对于每一个随机选出的近邻x^,分别与原样本按照如下的公式构建新的样本。

<<Python_实现>>
同样我们可以利用Python的第三方包imbalanced_learn实现SMOTE算法;如其官网给出的例子所"""
@author:Dylan; @desc:imbalanced_learn 2018/5/21 """ #-*- encoding:utf-8 -*- import matplotlib.pyplot as plt from sklearn.datasets import make_classification from sklearn.decomposition import PCA from imblearn.over_sampling import SMOTE print(__doc__) def plot_resampling(ax,X,y,title): c0=ax.scatter(X[y==0,0],X[y==0,1],label="Class #0",alpha=0.5) c1=ax.scatter(X[y==1,0],X[y==1,1],label="Class #1",alpha=0.5) ax.set_title(title) ax.spines['top'].set_visible(False) ax.spines['right'].set_visible(False) ax.get_xaxis().tick_bottom() ax.get_yaxis().tick_left() ax.spines['left'].set_position(('outward',10)) ax.spines['bottom'].set_position(('outward',10)) ax.set_xlim([-6,8]) ax.set_ylim([-6,6]) return c0,c1 if __name__=='__main__': X,y=make_classification(n_classes=2,class_sep=2,weights=[0.3,0.7], n_informative=3,n_redundant=1,flip_y=0, n_features=20,n_clusters_per_class=1,n_samples=80,random_state=10) ##使用PCA降维到两维,方便进行可视化 pca=PCA(n_components=2) X_vis=pca.fit_transform(X) ###运用SMOTE算法 kind=['regular','borderline1','borderline2','svm'] sm=[SMOTE(kind=k) for k in kind] X_resampled=[] y_resampled=[] X_res_vis=[] for method in sm: X_res,y_res=method.fit_sample(X,y) X_resampled.append(X_res) y_resampled.append(y_res) X_res_vis.append(pca.fit_transform(X_res)) f,((ax1,ax2),(ax3,ax4),(ax5,ax6))=plt.subplots(3,2) ##展示结果 ax2.axis('off') ax_res=[ax3,ax4,ax5,ax6] c0,c1=plot_resampling(ax1,X_vis,y,'original_set') for i in range(len(kind)): plot_resampling(ax_res[i],X_res_vis[i],y_resampled[i],'smote{}'.format(kind[i])) ax2.legend((c0,c1),('Class #0','Class #1'),loc='center',ncol=1,labelspacing=0.) plt.tight_layout() plt.show()
这段代码中,使用了sklearn简单是生成了一个不平衡的样本,使用了imblearn.over_sampling的SMOTE算法进行了过采样处理.生成结果如下图所示:
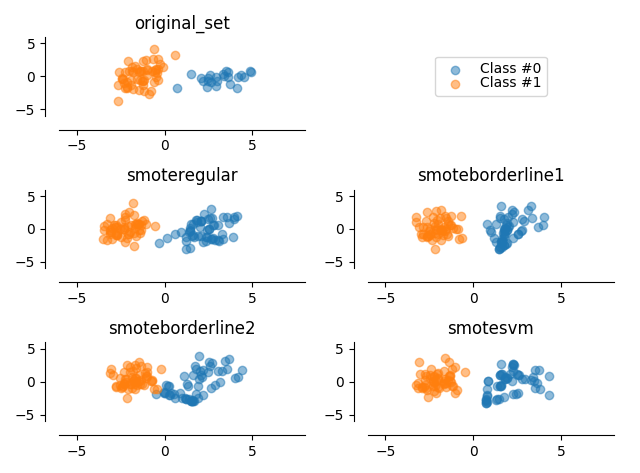
上图中.图1是原始数据的分布,图3-6分别是采样 'regular','borderline1','borderline2','svm'这四种类型处理方法的结果.个人倾向于使用svm.
使用SMOTE算法可以解决随机复制样本带来的问题,但是也可能会存在重叠的问题,因此基于smote算法提出了Borderline算法.
2.Borderline-SMOTE算法
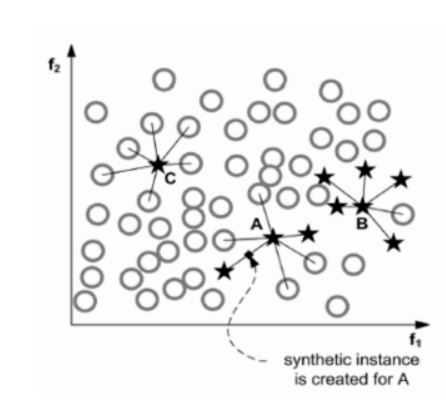
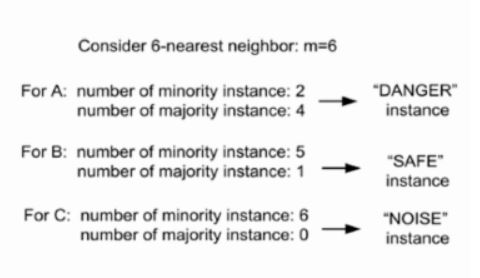
该算法对SMOTE算法中的少数类的最近邻加以限制,在Borderline-SMOTE中,若少数类样本的每个样本xi求k近邻,记作Si−knn,且Si−knn属于整个样本集合
S而不再是少数类样本,若满足 k/2<|si−knn∩smax|<k.即k近邻中超过一般是多数样本.那么就将xi加入到DANGER集合.显然该集合代表了接近分类边界的样本.
将DANGER当作SMOTE种子样本的输入生成新样本.特别地,当上述条件取右边界,即k近邻中全部样本都是多数类时此样本不会被选择为种样本生成新样本,
此情况下的样本为噪音。
当然还有一些其他的算法,例如ensemble,Informed InderSampling等,可以才有.Imblearn都对这些算法进行了实现.
参考自: https://blog.csdn.net/shine19930820/article/details/54143241;
http://contrib.scikit-learn.org/imbalanced-learn/stable/api.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号