sklearn中的metrics模块中的Classification metrics

metrics是sklearn用来做模型评估的重要模块，提供了各种评估度量，现在自己整理如下：

一.通用的用法：Common cases: predefined values

1.1 sklearn官网上给出的指标如下图所示：

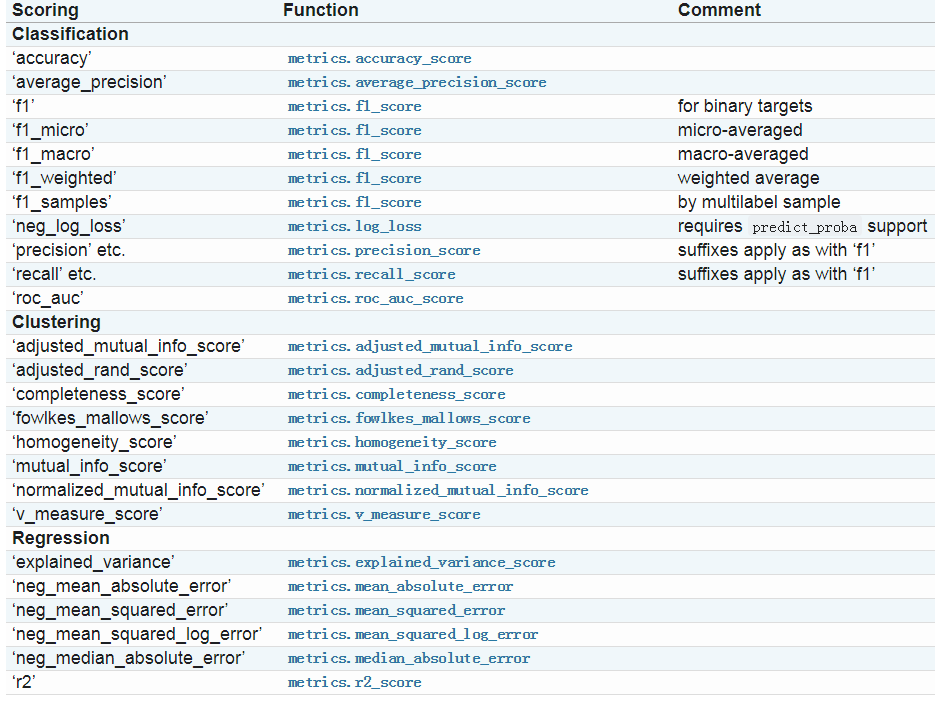
1.2除了上图中的度量指标以外，你还可以自定义一些度量指标：通过sklearn.metrics.make_scorer()方法进行定义；

make_scorer有两种典型的用法：

用法一：包装一些在metrics中已经存在的的方法，但是这种方法需要一些参数，例如fbeta_score方法，官网上给出的用法如下：

from sklearn.metrics import fbeta_score, make_scorer
ftwo_scorer = make_scorer(fbeta_score, beta=2)
from sklearn.model_selection import GridSearchCV
from sklearn.svm import LinearSVC
grid = GridSearchCV(LinearSVC(), param_grid={'C': [1, 10]}, scoring=ftwo_scorer)

第二种用法是完全的定义用户自定义的函数，可以接受一下几种参数：

　　1.你想用的python函数；

　　2、不论你提供的python函数返回的是socre或者是loss，if score：the higher the better；if loss： the lower the better

　　3、只为分类度量：无论你提供的python方法是不是需要连续的决策因素，默认为否

　　4.其他额外的参数，例如f1_score中的beta或者labels

例如官网上给出的例子：

import numpy as np
def my_custom_loss_func(ground_truth, predictions):
    diff = np.abs(ground_truth - predictions).max()
    return np.log(1 + diff)

# loss_func will negate the return value of my_custom_loss_func,
#  which will be np.log(2), 0.693, given the values for ground_truth
#  and predictions defined below.
loss  = make_scorer(my_custom_loss_func, greater_is_better=False)
score = make_scorer(my_custom_loss_func, greater_is_better=True)
ground_truth = [[1], [1]]
predictions  = [0, 1]
from sklearn.dummy import DummyClassifier
clf = DummyClassifier(strategy='most_frequent', random_state=0)
clf = clf.fit(ground_truth, predictions)
loss(clf,ground_truth, predictions) 
-0.69...
score(clf,ground_truth, predictions) 
0.69...

1.3 使用多重度量标准

sklearn也接受在GridSearchCV，RandomizedSearchCV和Cross_validate中接受多指标，有两种指定方式；

##方式1： 使用字符串的list    
scoring=['accuracy','precision']

### f方式2：使用dict进行mapping
from sklearn.metrics import accuracy_score
from sklearn.metrics import make_scorer
scoring = {'accuracy': make_scorer(accuracy_score),
           'prec': 'precision'}

注意：目前方式2（dict）模式只允许返回单一score的score方法，返回多个的需要进行加工处理，例如官方上给出的加工处理混淆矩阵的方法：

from sklearn.model_selection import cross_validate
from sklearn.metrics import confusion_matrix
# A sample toy binary classification dataset
X, y = datasets.make_classification(n_classes=2, random_state=0)
svm = LinearSVC(random_state=0)
def tp(y_true, y_pred): return confusion_matrix(y_true, y_pred)[0, 0]
def tn(y_true, y_pred): return confusion_matrix(y_true, y_pred)[0, 0]
def fp(y_true, y_pred): return confusion_matrix(y_true, y_pred)[1, 0]
def fn(y_true, y_pred): return confusion_matrix(y_true, y_pred)[0, 1]
scoring = {'tp' : make_scorer(tp), 'tn' : make_scorer(tn),
           'fp' : make_scorer(fp), 'fn' : make_scorer(fn)}
cv_results = cross_validate(svm.fit(X, y), X, y, scoring=scoring)
# Getting the test set true positive scores
print(cv_results['test_tp'])          
[12 13 15]
# Getting the test set false negative scores
print(cv_results['test_fn']) 
[5,4,1]

二：分类指标；

针对分类，sklearn也提供了大量的度量指标，而且针对不同的分类（二分类，多分类，）有不同的度量指标，官网截图如下：

2.1 从二分类到多分类问题：

像f1_score, roc_auc_score这种度量指标大多是针对二分类问题的，但是为了将二分类的度量指标延伸到多分类问题，数据将会看做是二分类问题的集合，也就是1vs all；有好几种方式来平衡不同类别的二分度量，通过使用average参数来进行设置。

（1）marco（宏平均）：当频繁的类别非常重要时，宏平均可以会突出他的性能表现；当然所有的类别同样重要是不现实的，因此宏平均可能会过度强调低频繁类别的低性能表现；

（2）weighted（权重）

（3）micro（微平均）：微平均可能在多标签的分类问题的首选

（4）samples（样本）：仅仅当多标签问题是可以采用。

多分类问题转换到二分类问题就是采用1vs all的方式；

2.2 准确率（accuracy）

　　采用accuracy_score来计算模型的accuracy，计算公式如下：

　　　　 $\texttt{accuracy}(y, \hat{y}) = \frac{1}{n_\text{samples}} \sum_{i=0}^{n_\text{samples}-1} 1(\hat{y}_i = y_i)$ ，其中 $\hat{y}_i$ 表示预测y值，yi表示实际的y值；

##
import numpy as np
from sklearn.metrics import accuracy_score
y_pred = [0, 2, 1, 3]
y_true = [0, 1, 2, 3]
accuracy_score(y_true, y_pred)
0.5
accuracy_score(y_true, y_pred, normalize=False)
2
###多分类问题
accuracy_score(np.array([[0, 1], [1, 1]]), np.ones((2, 2)))
0.5

2.3混淆矩阵

混淆矩阵是评价分类问题的一个典型度量，在sklearn中使用 confusion_matrix；

from sklearn.metrics import confusion_matrix
y_true = [2, 0, 2, 2, 0, 1]
y_pred = [0, 0, 2, 2, 0, 2]
confusion_matrix(y_true, y_pred)
array([[2, 0, 0],
       [0, 0, 1],
       [1, 0, 2]])

混淆矩阵Rij（多分类）的含义表示类别i被预测成类别j的次数，因此Rii表示被正确分类的次数；

对于二分类问题，混淆矩阵用来表示TN，TP，FN，FP；

y_true = [0, 0, 0, 1, 1, 1, 1, 1]
y_pred = [0, 1, 0, 1, 0, 1, 0, 1]
tn, fp, fn, tp = confusion_matrix(y_true, y_pred).ravel()
tn, fp, fn, tp
(2, 1, 2, 3)

官网上提供的混淆矩阵的可视化例子：http://scikit-learn.org/stable/auto_examples/model_selection/plot_confusion_matrix.html#sphx-glr-auto-examples-model-selection-plot-confusion-matrix-py

2.4 Classification report

Classification report展示了分类的主要度量指标，如下面例子所示：

from sklearn.metrics import classification_report
y_true = [0, 1, 2, 2, 0]
y_pred = [0, 0, 2, 1, 0]
target_names = ['class 0', 'class 1', 'class 2']
print(classification_report(y_true, y_pred, target_names=target_names))
             precision    recall  f1-score   support

    class 0       0.67      1.00      0.80         2
    class 1       0.00      0.00      0.00         1
    class 2       1.00      0.50      0.67         2

avg / total       0.67      0.60      0.59         5

2.5 Hamming loss

Hamming loss计算预测结果和实际结果的海明距离，计算公式如下：

$L_{Hamming}(y, \hat{y}) = \frac{1}{n_\text{labels}} \sum_{j=0}^{n_\text{labels} - 1} 1(\hat{y}_j \not= y_j)$ ，简单的理解就是预测样本中误差总数除以样本总数

例子：

from sklearn.metrics import hamming_loss
y_pred = [1, 2, 3, 4]
y_true = [2, 2, 3, 4]
hamming_loss(y_true, y_pred)
0.25

##在多标签分类中同样适合
hamming_loss(np.array([[0, 1], [1, 1]]), np.zeros((2, 2)))
0.75

2.6 Jaccard 相关系数：

Jaccard相关系数在推荐系统中经常使用，可以理解为预测正确的个数除以总的样本数，所以在二分类问题中，Jaccard系数和准确率是一样的。

$J(y_i, \hat{y}_i) = \frac{|y_i \cap \hat{y}_i|}{|y_i \cup \hat{y}_i|}.$ ，

例子：

import numpy as np
from sklearn.metrics import jaccard_similarity_score
y_pred = [0, 2, 1, 3]
y_true = [0, 1, 2, 3]
jaccard_similarity_score(y_true, y_pred)
0.5
jaccard_similarity_score(y_true, y_pred, normalize=False)
2
##multilabel
jaccard_similarity_score(np.array([[0, 1], [1, 1]]), np.ones((2, 2)))
0.75

2.7 precision，召回率，F系数等

（1）精准率（precision）：正确预测为正例的样本数占全部预测为正例的样本数的比例；

（2）召回率：正例样本中预测正确的样本占实际正例样本数量的比例；

（3）F系数同时兼顾了分类模型的准确率和召回率。F1分数可以看作是模型准确率和召回率的一种加权平均，它的最大值是1，最小值是0。

计算公式：

又称平衡F分数（balanced F Score），它被定义为精确率和召回率的调和平均数。公式为：

；

更一般的，我们定义

分数为

(4).precision_recall_curve:准确率召回率曲线

(5).average_precision_score:计算平均准确率（AP）,结果在0-1之间，越大越好：

计算公式：

$\text{AP} = \sum_n (R_n - R_{n-1}) P_n$ ，其中where $P_n$ and $R_n$ are the precision and recall at the nth threshold.

对于二分类问题，计算公式：

$\text{precision} = \frac{tp}{tp + fp},$

$\text{recall} = \frac{tp}{tp + fn},$

$F_\beta = (1 + \beta^2) \frac{\text{precision} \times \text{recall}}{\beta^2 \text{precision} + \text{recall}}.$

小例子：

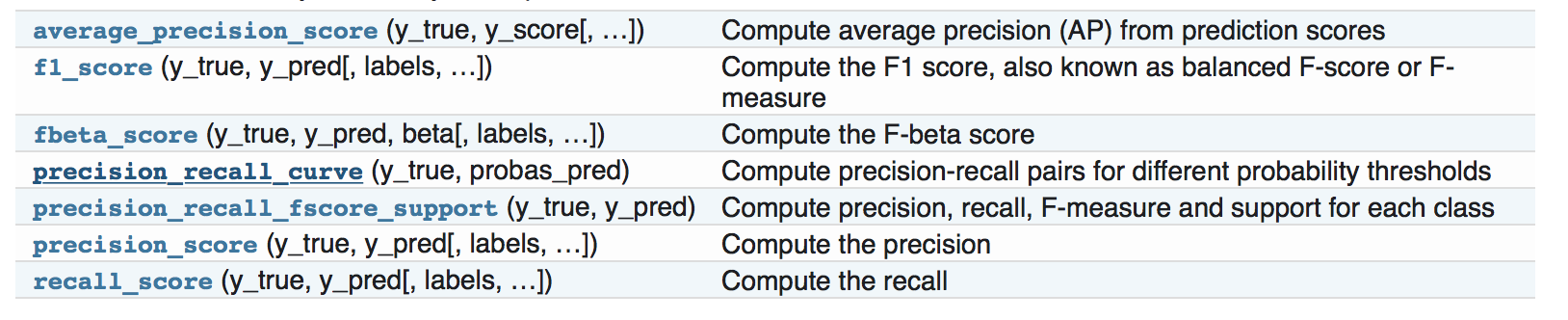
>>> from sklearn import metrics
>>> y_pred = [0, 1, 0, 0]
>>> y_true = [0, 1, 0, 1]
>>> metrics.precision_score(y_true, y_pred)
1.0
>>> metrics.recall_score(y_true, y_pred)
0.5
>>> metrics.f1_score(y_true, y_pred)  
0.66...
>>> metrics.fbeta_score(y_true, y_pred, beta=0.5)  
0.83...
>>> metrics.fbeta_score(y_true, y_pred, beta=1)  
0.66...
>>> metrics.fbeta_score(y_true, y_pred, beta=2) 
0.55...
>>> metrics.precision_recall_fscore_support(y_true, y_pred, beta=0.5)  
(array([ 0.66...,  1.        ]), array([ 1. ,  0.5]), array([ 0.71...,  0.83...]), array([2, 2]...))


>>> import numpy as np
>>> from sklearn.metrics import precision_recall_curve
>>> from sklearn.metrics import average_precision_score
>>> y_true = np.array([0, 0, 1, 1])
>>> y_scores = np.array([0.1, 0.4, 0.35, 0.8])
>>> precision, recall, threshold = precision_recall_curve(y_true, y_scores)
>>> precision  
array([ 0.66...,  0.5       ,  1.        ,  1.        ])
>>> recall
array([ 1. ,  0.5,  0.5,  0. ])
>>> threshold
array([ 0.35,  0.4 ,  0.8 ])
>>> average_precision_score(y_true, y_scores)  
0.83...

对于多类别分类和多标签分类，同样提供的一样的评价指标；

例子：

>>> from sklearn import metrics
>>> y_true = [0, 1, 2, 0, 1, 2]
>>> y_pred = [0, 2, 1, 0, 0, 1]
>>> metrics.precision_score(y_true, y_pred, average='macro')  
0.22...
>>> metrics.recall_score(y_true, y_pred, average='micro')
... 
0.33...
>>> metrics.f1_score(y_true, y_pred, average='weighted')  
0.26...
>>> metrics.fbeta_score(y_true, y_pred, average='macro', beta=0.5)  
0.23...
>>> metrics.precision_recall_fscore_support(y_true, y_pred, beta=0.5, average=None)
... 
(array([ 0.66...,  0.        ,  0.        ]), array([ 1.,  0.,  0.]), array([ 0.71...,  0.        ,  0.        ]), array([2, 2, 2]...))

2.8 ROC曲线

ROC曲线是建模结果比较熟悉的一中展示方式：

例如如下代码：

import numpy as np
from sklearn.metrics import roc_curve
from sklearn.datasets import load_iris
from sklearn import svm
from sklearn.linear_model import LogisticRegression
from sklearn.cross_validation import train_test_split
from sklearn.metrics import roc_auc_score
from sklearn.metrics import roc_curve
import matplotlib.pyplot as plt

data=load_iris()
###两分类
X,y=data.data,data.target


X_train,X_test,y_train,y_test=train_test_split(X,y)
est=svm.SVC(probability=True)
model=est.fit(X_train,y_train)
y_score=model.decision_function(X_test)
fpr1,tpr1,thresholds1=roc_curve(y_test,model.predict_proba(X_test)[:,1],pos_label=1)

lr=LogisticRegression()
lr.fit(X_train,y_train)
fpr2,tpr2,thresholds2=roc_curve(y_test,lr.predict_proba(X_test)[:,1],pos_label=1)

plt.plot(fpr1,tpr1,linewidth=1,label='ROC of svm')
plt.plot(fpr2,tpr2,linewidth=1,label='ROC of LR')
plt.xlabel('FPR')
plt.ylabel('TPR')
plt.plot([0,1],[0,1],linestyle='--')
plt.legend(loc=4)
plt.show()

结果如上图所示。

posted on 2018-04-17 19:29 波比12 阅读(4702) 评论(0) 编辑收藏举报

刷新页面返回顶部

波比12

sklearn中的metrics模块中的Classification metrics

导航

公告