Sklearn库例子2：分类——线性回归分类（Line Regression ）例子

线性回归：通过拟合线性模型的回归系数W =（w_1，…，w_p）来减少数据中观察到的结果和实际结果之间的残差平方和，并通过线性逼近进行预测。

从数学上讲，它解决了下面这个形式的问题：     

LinearRegression()模型在Sklearn.linear_model下，他主要是通过fit（x,y）的方法来训练模型，其中x为数据的属性，y为所属类型。线性模型的回归系数W会保存在他的coef_方法中。

例如：

>>> from sklearn import linear_model
>>> clf = linear_model.LinearRegression()
>>> clf.fit ([[0, 0], [1, 1], [2, 2]], [0, 1, 2])
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
>>> clf.coef_
array([ 0.5,  0.5])

 实例：

使用的数据集为Sklearn.dataset.load_diabetes()一个关于糖尿病的数据集。

为了说明这个回归技术的一个二维图，例子仅仅使用了糖尿病数据集的第一个特征。

代码如下：

# -*- encoding:utf-8 -*-
"""
Line Regression Example
DataBase:diavetes
"""

import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets,linear_model
import time

a=time.time()
####加载数据集
diabetes=datasets.load_diabetes()

####仅仅使用一个特征：
diabetes_X=diabetes.data[:,np.newaxis,2]

###s数据划分训练集和测试集
diabetes_X_train=diabetes_X[:-20]
diabetes_X_test=diabetes_X[-20:]

###目标划分为训练集和测试集
diabetes_y_train=diabetes.target[:-20]
diabetes_y_test=diabetes.target[-20:]

###训练模型
regr=linear_model.LogisticRegression()
regr.fit(diabetes_X_train,diabetes_y_train)

###回归系数
print('Coefficients:\n',regr.coef_)

###均方误差
print('the mean sqare error:%.2f' %np.mean((regr.predict(diabetes_X_test)-diabetes_y_test)**2))
print('Variance score:%.2f' %regr.score(diabetes_X_test,diabetes_y_test))
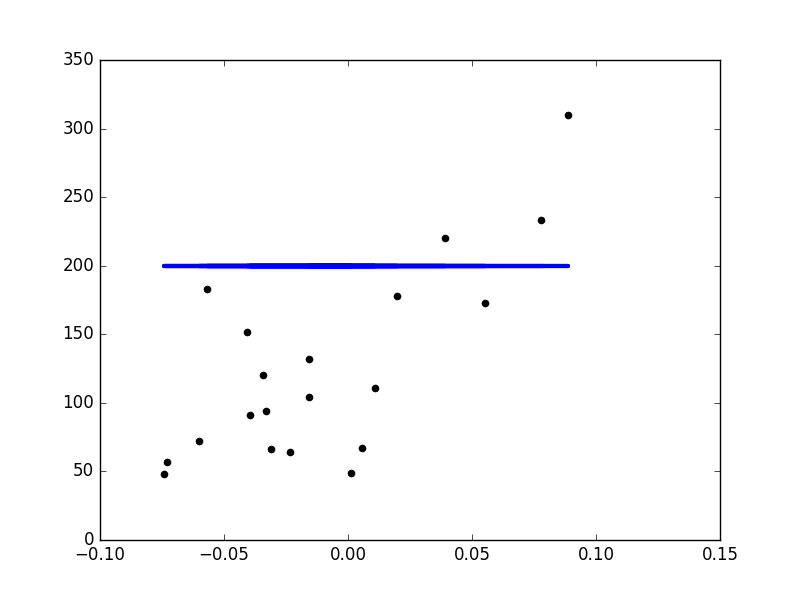
##散点图
plt.scatter(diabetes_X_test,diabetes_y_test,color='black')
plt.plot(diabetes_X_test,regr.predict(diabetes_X_test),color='blue',linewidth=3)
plt.xticks()
plt.yticks()
b=time.time()
print('the running time is %.2f' %(b-a))
plt.show()

 实验结果：

Coefficients:
 [ 938.23786125]
Residual sum of squares: 2548.07
Variance score: 0.47
the running time is 0.31