Leetcode 300. 最长递增子序列

https://leetcode.cn/problems/longest-increasing-subsequence/description/

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的
子序列。

示例 1：
输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。
示例 2：
输入：nums = [0,1,0,3,2,3]
输出：4
示例 3：
输入：nums = [7,7,7,7,7,7,7]
输出：1
 
提示：
1 <= nums.length <= 2500
-104 <= nums[i] <= 104

进阶：
你能将算法的时间复杂度降低到 O(n log(n)) 吗?

解答
dp解答
dp[x]为 索引x的数字结尾能到达的最长严格递增子序列的长度
所以 y是小于x的索引 如果nums[x] >nums[y],说明nums[x]可以加在以nums[y]结尾的严格递增子序列后面,
那么长度就是dp[x]=dp[y]+1;

代码如下

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int dp[3000]; int ans=1;
        for(int i= 0;i<nums.size();i++){
            dp[i]= 1;
            for(int j=0;j<i;j++){
                if(nums[j]<nums[i]){
                    dp[i]=max(dp[i],dp[j]+1);
                }
            }
            ans=max(ans,dp[i]);
        }

        return ans;
    }
};

时间复杂度是O(n^2)

还有一种O(nlogn)的解法
arr[N] 表示最长严格递增子序列第N为放置的数
我们一次遍历输入的数组nums,每次将数字放入arr最前端大于等于自己的数。
从贪心的角度，我们每次给后面的nums提供更小的前缀，那么严格递增子序列久尽可能更长
比如说我们一开始得到的递增子序列是10 101， 我们通过一系列操作就可以替换成 2 5 那么后面就可以添加其他元素。长度达到4
而10 101这个子序列长度不可能增加了

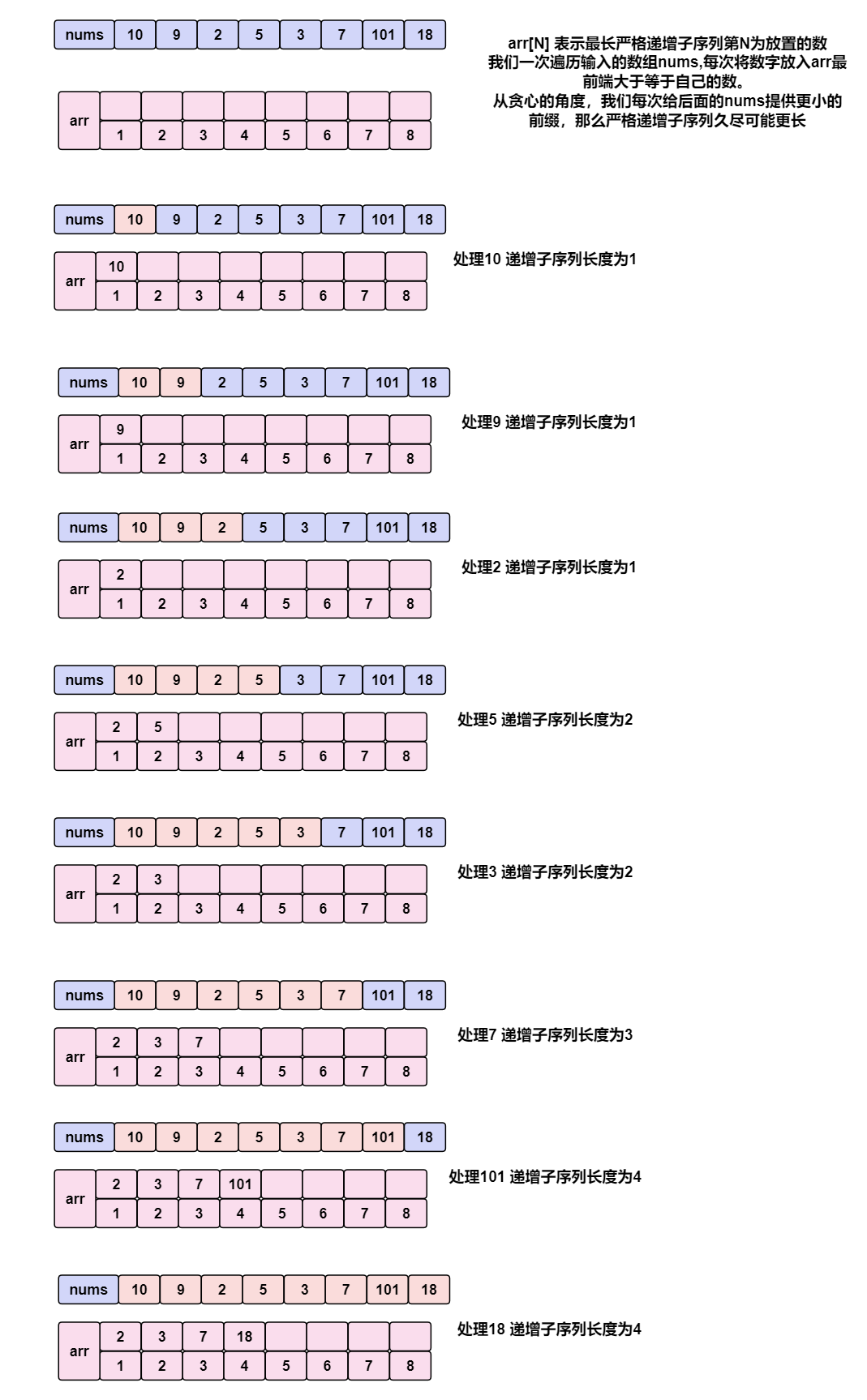
代码里 选择arr里合适的插入位置 使用的是二分.

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int ans = 1;
        int [3000];  memset(arr, 0x3f, sizeof arr);
        arr[0] = 0;

        for (int i = 0; i < nums.size(); i++) {
            int l = 1; int r = nums.size();
            while (l < r) {
                int mid = l + r >> 1;
                if (arr[mid] >= nums[i]) r = mid;
                else l = mid + 1;
            }
            arr[l] = nums[i];
            ans = max(ans, l );
        }

        return ans;
    }
};

我的视频题解空间