Leetcode 072 编辑距离 dp
地址 https://leetcode-cn.com/problems/edit-distance/
给你两个单词 word1 和 word2,请你计算出将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
插入一个字符
删除一个字符
替换一个字符
示例 1:
输入:word1 = "horse", word2 = "ros"
输出:3
解释:
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')
示例 2:
输入:word1 = "intention", word2 = "execution"
输出:5
解释:
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')
提示:
0 <= word1.length, word2.length <= 500
word1 和 word2 由小写英文字母组成
解答
编辑距离是动态规划一个经典模板。
首先明确,我们不必采取添加字母的做法。
字符串A添加字母与字符串B删除字母效果相同。 同理,字符串B添加字母与字符串A删除字母效果相同.
那么我们只需要考虑 变换字母和删除字母的情况即可.
我们使用dp[i][j] 表示字符串A[0~i]与字符串B[0~j]匹配的最小操作数。
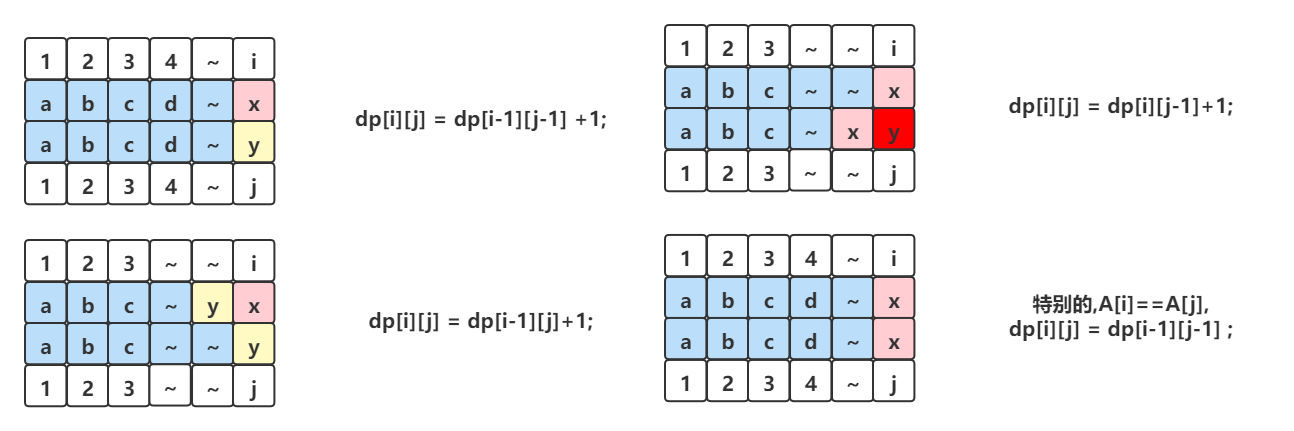
那么我们可以将字母A[i]转化成字母B[j] ,dp[i][j] 从字符串A[0~i-1]与字符串B[0~j-1]的操作数转化, dp[i][j] = dp[i-1][j-1] +1;
也可以考虑将字母A[i]删除,dp[i][j] 从字符串A[0~i-1]与字符串B[0~j]的操作数转化, dp[i][j] = dp[i-1][j]+1;
或者将字母B[j]删除,dp[i][j] 从字符串A[0~i]与字符串B[0~j-1]的操作数转化 , dp[i][j] = dp[i][j-1]+1;
特别地,如果字符A[i]与B[j]相同 那么还要考虑 dp[i][j] = dp[i-1][j-1];
以上情况取最小操作数字.
class Solution {
public:
vector<vector<int>> dp;
int minDistance(string word1, string word2) {
int len = max(word1.size(), word2.size());
dp = vector<vector<int>>(len+10,vector<int>(len+10));
word1.insert(word1.begin(), '#');
word2.insert(word2.begin(), '@');
for (int i = 0; i <= word1.size(); i++) { dp[i][0] = i; }
for (int i = 0; i <= word2.size(); i++) { dp[0][i] = i; }
for (int i = 1; i <= word1.size(); i++) {
for (int j = 1; j <= word2.size(); j++) {
dp[i][j] = min(dp[i][j - 1]+1, dp[i - 1][j]+1);
if (word1[i] == word2[j]) {
dp[i][j] = min(dp[i][j], dp[i - 1][j - 1]);
}
else {
dp[i][j] = min(dp[i][j], dp[i - 1][j - 1] + 1);
}
}
}
return dp[word1.size()][word2.size()];
}
};
作 者: itdef
欢迎转帖 请保持文本完整并注明出处
技术博客 http://www.cnblogs.com/itdef/
B站算法视频题解
https://space.bilibili.com/18508846
qq 151435887
gitee https://gitee.com/def/
欢迎c c++ 算法爱好者 windows驱动爱好者 服务器程序员沟通交流
如果觉得不错,欢迎点赞,你的鼓励就是我的动力


欢迎转帖 请保持文本完整并注明出处
技术博客 http://www.cnblogs.com/itdef/
B站算法视频题解
https://space.bilibili.com/18508846
qq 151435887
gitee https://gitee.com/def/
欢迎c c++ 算法爱好者 windows驱动爱好者 服务器程序员沟通交流
如果觉得不错,欢迎点赞,你的鼓励就是我的动力





 浙公网安备 33010602011771号
浙公网安备 33010602011771号