papamelon 328. 电路板 Bridging signals（挑战程序设计竞赛）

地址 https://www.papamelon.com/problem/328


解答
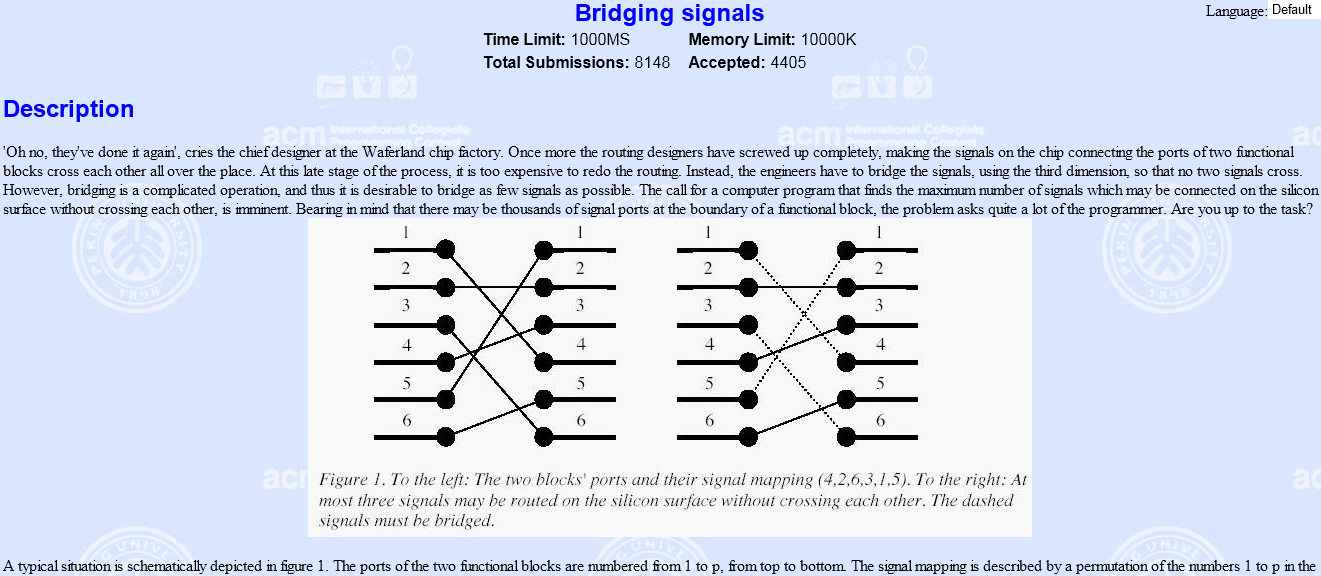
以6个接口为例
左端 1 2 3 4 5 6端口对应
右端 4 2 6 3 1 5 端口
如图 左1连接的是右5 如果选择这条接线
那么左端其他接口就不能连接右端5以前的接口了，否则就会接线交叉。

按照这个规则，其实我们就是求解。
为了接线不交叉的情况下接入更多的接口， 等同于查找左端可以连接右端接口数字的最长上升子序列

于是有了solve1的代码，但是时间复杂度是O(n^2),n=40000,结果大大超出10^8，肯定TLE了

于是采用单调队列优化,dp[i]表示当前获得的长度为i的最长上升子序列的结尾元素。
每次加入元素时检查dp数组，若dp数组尾端小于元素，元素直接加入dp数组尾端，否则的话则查找dp数组中第一个大于待加入元素的位置，新元素替换进去；最后dp数组的长度
就是最长上升子序列长度；

因为dp数组内的元素单调，所以可以二分查找，整体复杂u度O(n*logn)
代码见solve2

#include <iostream>
#include <memory.h>
#include <algorithm>

using namespace std;

const int N = 40010;

int A[N];
int dp[N];
int t, n;

void solve1() {

	cin >> t;
	while (t--) {
		memset(A, 0, sizeof A);
		memset(dp, 0, sizeof dp);
		cin >> n;

		for (int i = 1; i <= n; i++) {
			cin >> A[i];
		}
		int ans = 0;
		for (int i = 1; i <= n; i++) {
			for (int j = i - 1; j >= 0; j--) {
				if (A[i] > A[j]) {
					dp[i] = max(dp[i], dp[j] + 1);
				}
			}
			ans = max(ans, dp[i]);
		}
		cout << ans << endl;
	}


	return ;
}



/*
O(n^2) tle  进行优化
O(nlogn)
每次加入元素时检查栈顶，若栈顶小于元素，直接加入，否则的话则查找栈中第一个大于待加入元素的元素，换掉它；最后栈的容量就是长度；
因为栈内的元素单调，所以可以二分查找，O(logn)O(logn)替换O(n)O(n)达到优化；
*/

int bsearch(int target, int len) {
	int l = 1; int r = len;
	while (l < r) {
		int mid = (l + r) >> 1;
		if (dp[mid]>=target) r = mid;
		else  l = mid + 1;
	}

	return l;
}

void solve2() {
	cin >> t;
	while (t--) {
		memset(A, 0, sizeof A);
		memset(dp, 0, sizeof dp);
		cin >> n;

		for (int i = 1; i <= n; i++) {
			cin >> A[i];
		}
		int idx = 1; dp[idx] = A[idx];
		for (int i = 2; i <= n; i++) {
			if (A[i] > dp[idx]) {
				dp[idx + 1] = A[i]; idx++;
			}
			else {
				int pos = bsearch(A[i],idx);
				dp[pos] = A[i];
			}
		}

		cout << idx << endl;
	}

	return ;
}

int main()
{
	//solve1(); //tle
	solve2();

	return 0;
}

我的视频题解空间