Leetcode 576. 出界的路径数 dp

地址 https://leetcode-cn.com/problems/out-of-boundary-paths/

给你一个大小为 m x n 的网格和一个球。球的起始坐标为 [startRow, startColumn] 。
你可以将球移到在四个方向上相邻的单元格内（可以穿过网格边界到达网格之外）。你 最多 可以移动 maxMove 次球。
给你五个整数 m、n、maxMove、startRow 以及 startColumn ，找出并返回可以将球移出边界的路径数量。
因为答案可能非常大，返回对 109 + 7 取余 后的结果。


示例 1：

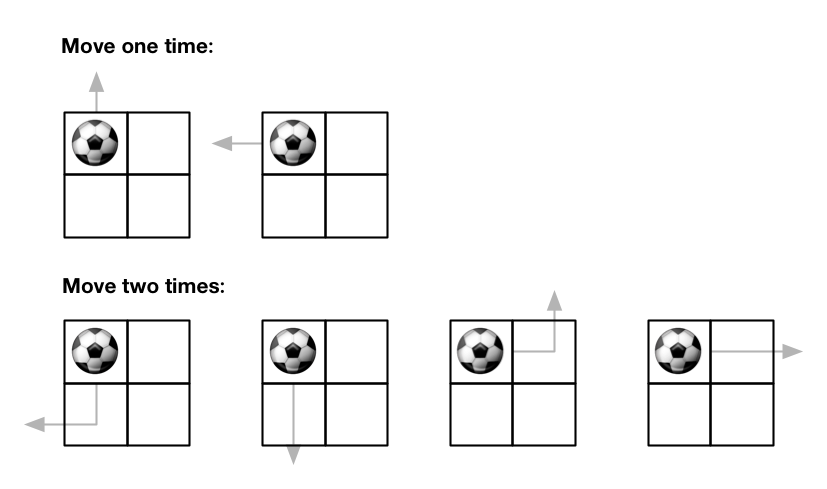
输入：m = 2, n = 2, maxMove = 2, startRow = 0, startColumn = 0
输出：6


示例 2：

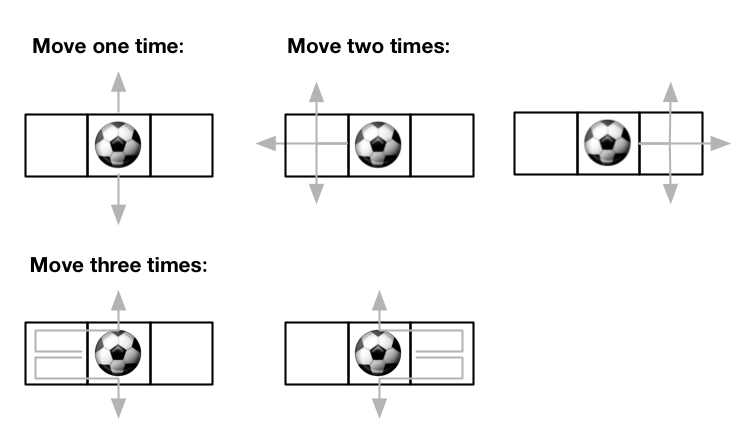
输入：m = 1, n = 3, maxMove = 3, startRow = 0, startColumn = 1
输出：12
 
提示：
1 <= m, n <= 50
0 <= maxMove <= 50
0 <= startRow < m
0 <= startColumn < n

解答

dp[x][y][z]代表的是 xy点走z步恰好走出边界的方案数

class Solution {
public:
	const int MOD = 1e9 + 7;
	vector<vector<vector<int>>> dp;
	
	int findPaths(int m, int n, int N, int x, int y) {
		dp.resize(m, vector<vector<int>>(n, vector<int>(N + 10)));
		if (N == 0) return 0;

		for (int i = 0; i < m; i++) {
			dp[i][0][1]++;
			dp[i][n - 1][1]++;
		}

		for (int j = 0; j < n; j++) {
			dp[0][j][1] ++;
			dp[m - 1][j][1]++;
		}

		for (int k = 1; k <= N; k++) {
			for (int a = 0; a < m; a++) {
				for (int b = 0; b < n; b++) {
					if (a > 0) {
						dp[a][b][k] += dp[a - 1][b][k - 1]; dp[a][b][k] %= MOD;
					}
					if (b > 0) {
						dp[a][b][k] += dp[a][b-1][k - 1]; dp[a][b][k] %= MOD;
					}
					if(a<m-1){
						dp[a][b][k] += dp[a + 1][b][k - 1]; dp[a][b][k] %= MOD;
					}
					if(b<n-1){
						dp[a][b][k] += dp[a][b+1][k - 1];	dp[a][b][k] %= MOD;
					}

					//printDP(a,b, k);
				}
			}
		}

		int ans = 0;
		for (int i = 0; i <= N; i++) {
			ans += dp[x][y][i] % MOD;
			ans %= MOD;
		}

		return ans;
	}
};

记忆化搜索 dp[x][y][z]代表的是 xy点能走z步所有走出边界的方案数

class Solution {
public:
	const int MOD = 1e9 + 7;
	vector<vector<vector<int>>> dp;
	int addx[4] = { 1,0,-1,0 };
	int addy[4] = { 0,1,0,-1 };

	void PrintDP(int x, int y, int z) {
		printf("dp[%d][%d][%d] = %d \n",x,y,z,dp[x][y][z]);
	}

	int findPathsInner(int m, int n, int move, int x, int y) {
		if (x < 0 || x >= m || y < 0 || y >= n) return 1;
		if (move == 0) return 0;
		int& v = dp[x][y][move]; if (v != -1) return v;
		v = 0;
		for (int i = 0; i < 4; i++) {
			int newx = x + addx[i]; int newy = y + addy[i];
			v+= findPathsInner(m, n, move - 1, newx, newy);
			v %= MOD;
		}

		PrintDP(x, y, move);
		return v;
	}

	int findPaths(int m, int n, int N, int x, int y) {
		dp.resize(m, vector<vector<int>>(n, vector<int>(N + 1,-1)));
		if (N == 0) return 0;

		int ans = findPathsInner(m, n, N , x, y);

		return  ans;
	}
};