LeetCode 1139. 最大的以 1 为边界的正方形 前缀和

地址 https://leetcode-cn.com/problems/largest-1-bordered-square/

给你一个由若干 0 和 1 组成的二维网格 grid，请你找出边界全部由 1 组成的最大 正方形 子网格，并返回该子网格中的元素数量。如果不存在，则返回 0。

 

示例 1：

输入：grid = [[1,1,1],[1,0,1],[1,1,1]]
输出：9
示例 2：

输入：grid = [[1,1,0,0]]
输出：1
 

提示：

1 <= grid.length <= 100
1 <= grid[0].length <= 100
grid[i][j] 为 0 或 1

算法1
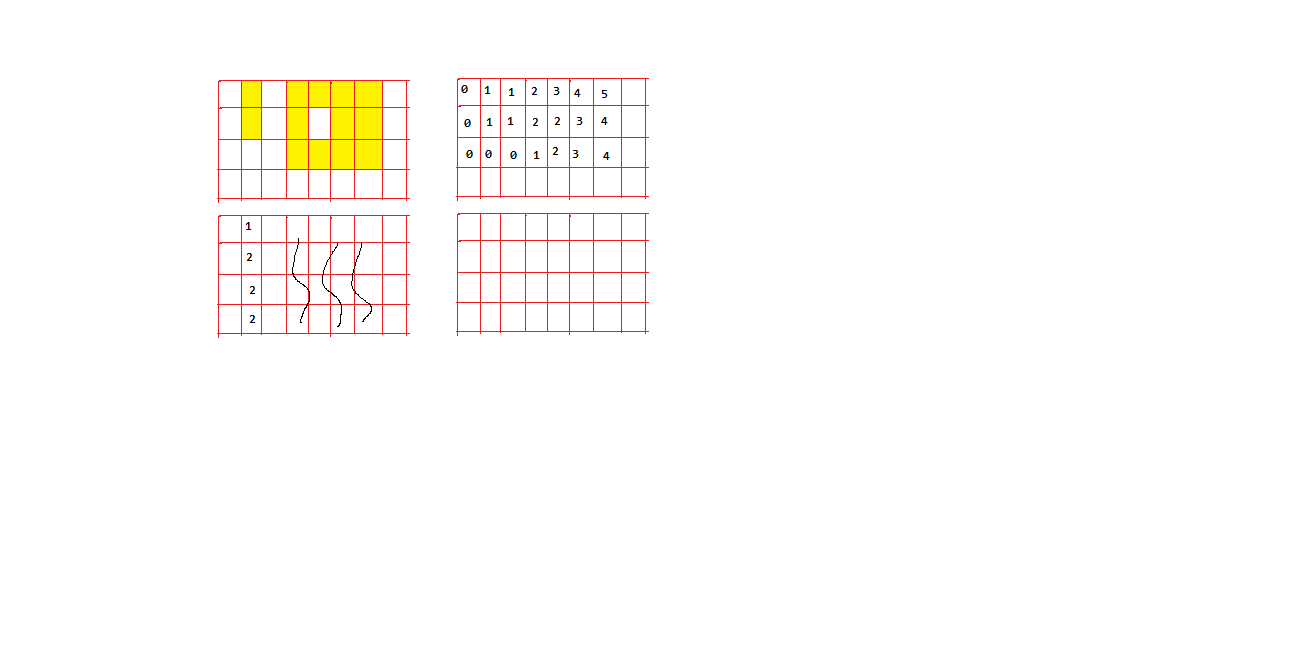
使用前缀和记录 行与列到达该坐标1的总数 加快查询效率
然后遍历每个正方形 查看每条边的1的总数是否达到长度判断边是否全1
示意图

class Solution {
public:


int presumCol[150][150];
int presumRow[150][150];
int ans =0;
int n, m;

bool CheckSquard(int startx, int starty, int len)
{
    int endx = startx + len ;
    int endy = starty + len ;

    startx++; starty++;

    if (endx <= n && endy <= m) {
        if (presumRow[startx][endy] - presumRow[startx][starty-1] == len && 
            presumRow[endx][endy] - presumRow[endx][starty - 1] == len && 
            presumCol[endx][starty] - presumCol[startx-1][starty] == len &&
            presumCol[endx][endy] - presumCol[startx-1][endy] == len)
        {
            ans = len * len;
            return true;
        }
    }



    return false;
}

int largest1BorderedSquare(vector<vector<int>>& grid) {
    if (grid.empty() || grid[0].empty()) return 0;
    n = grid.size();
    m = grid[0].size();
    //计算行列为单位的  前面有多少个1 的前缀和

    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            presumRow[i][j] = presumRow[i][j - 1] + grid[i - 1][j - 1];
        }
    }

    for (int y = 1; y <= m; y++) {
        for (int x = 1; x <= n; x++) {
            presumCol[x][y] = presumCol[x-1][y] + grid[x - 1][y - 1];
        }
    }

    int lenlimit = min(n, m);

    for (int len = lenlimit; len > 0; len--) {
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (CheckSquard(i, j, len)) {
                    return ans;
                }
            }
        }
    }


    return ans;
}


};