AcWing 1027. 方格取数 dp
地址 https://www.acwing.com/solution/content/17900/
题目描述
设有 N×N 的方格图,我们在其中的某些方格中填入正整数,而其它的方格中则放入数字0。
如下图所示:
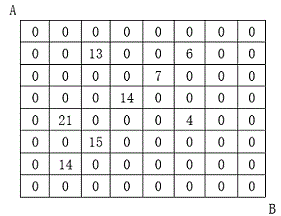
某人从图中的左上角 A 出发,可以向下行走,也可以向右行走,直到到达右下角的 B 点。 在走过的路上,他可以取走方格中的数(取走后的方格中将变为数字0)。 此人从 A 点到 B 点共走了两次,试找出两条这样的路径,使得取得的数字和为最大。 输入格式 第一行为一个整数N,表示 N×N 的方格图。 接下来的每行有三个整数,第一个为行号数,第二个为列号数,第三个为在该行、该列上所放的数。 行和列编号从 1 开始。 一行“0 0 0”表示结束。 输出格式 输出一个整数,表示两条路径上取得的最大的和。 数据范围 N≤10 输入样例: 8 2 3 13 2 6 6 3 5 7 4 4 14 5 2 21 5 6 4 6 3 15 7 2 14 0 0 0 输出样例: 67
双dp
由于第一次移动的选择会影响第二次的移动选择
那么考虑两次同时移动
dp[n][i][j]
n表示移动多少不 i表示第一次移动的横坐标 j表示第二次移动的横坐标
只是的dp意义为 移动n步 第一次移动到n-i,i的位置 第二次移动到n-j,j的位置上
所能取到的最大的数字
val 表示最后所在坐标里的数字 f[k][x1][x2] = max(f[k][x1][x2],f[k-1][x1-1][x2-1]+val); f[k][x1][x2] = max(f[k][x1][x2], f[k - 1][x1 - 1][x2] + val); f[k][x1][x2] = max(f[k][x1][x2], f[k - 1][x1][x2-1] + val); f[k][x1][x2] = max(f[k][x1][x2], f[k - 1][x1][x2] + val);
c++代码
// 11235.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。 // #include <iostream> #include <algorithm> using namespace std; /* 输入样例: 8 2 3 13 2 6 6 3 5 7 4 4 14 5 2 21 5 6 4 6 3 15 7 2 14 0 0 0 输出样例: 67 */ const int N = 15; int g[N][N]; int n; int f[N + N][N][N]; void solve() { for (int k = 2; k <= (2*n); k++) { for (int x1 = 1; x1 <= n; x1++) { for (int x2 = 1; x2 <= n; x2++) { int y1 = k - x1; int y2 = k - x2; if (x1 >= 1 && x1 <= n && y1 >= 1 && y1 <= n && x2 >= 1 && x2 <= n && y2 >= 1 && y2 <= n) { //================================================================ int val = g[x1][y1]; if (x1 != x2) val += g[x2][y2]; f[k][x1][x2] = max(f[k][x1][x2],f[k-1][x1-1][x2-1]+val); f[k][x1][x2] = max(f[k][x1][x2], f[k - 1][x1 - 1][x2] + val); f[k][x1][x2] = max(f[k][x1][x2], f[k - 1][x1][x2-1] + val); f[k][x1][x2] = max(f[k][x1][x2], f[k - 1][x1][x2] + val); } } } } cout << f[2 * n][n][n]; return ; } int main() { cin >> n; while (1) { int a, b, w; cin >> a >> b >> w; if (a == b && b == w && w == 0) break; g[a][b] = w; } solve(); return 0; }
作 者: itdef
欢迎转帖 请保持文本完整并注明出处
技术博客 http://www.cnblogs.com/itdef/
B站算法视频题解
https://space.bilibili.com/18508846
qq 151435887
gitee https://gitee.com/def/
欢迎c c++ 算法爱好者 windows驱动爱好者 服务器程序员沟通交流
如果觉得不错,欢迎点赞,你的鼓励就是我的动力


欢迎转帖 请保持文本完整并注明出处
技术博客 http://www.cnblogs.com/itdef/
B站算法视频题解
https://space.bilibili.com/18508846
qq 151435887
gitee https://gitee.com/def/
欢迎c c++ 算法爱好者 windows驱动爱好者 服务器程序员沟通交流
如果觉得不错,欢迎点赞,你的鼓励就是我的动力





 浙公网安备 33010602011771号
浙公网安备 33010602011771号