【组合数+Lucas定理模板】HDU 3037 Saving
acm.hdu.edu.cn/showproblem.php?pid=3037
【题意】
- m个松果,n棵树
- 求把最多m个松果分配到最多n棵树的方案数
- 方案数有可能很大,模素数p
- 1 <= n, m <= 1000000000, 1 < p < 100000
【思路】
- 答案为C(n+m,m)%p
-
对于C(n, m) mod p。这里的n,m,p(p为素数)都很大的情况。就不能再用C(n, m) = C(n - 1,m) + C(n - 1, m - 1)的公式递推了。这里用到Lucas定理。
![]()
-
下面证明为什么答案是C(n+m,m):
- 把i个松果分配到最多n棵树的方案数是:C(i+n-1,i)(相当于x1+x2+......+xn=i的解的个数,用插板法,插n-1个板,共i+n-1个位置选i个1,因为xi可能是0,所以满足最多n棵树)
-
现在就需要求不大于m的,相当于对i = 0,1...,m对C(n+i-1,i)求和,根据公式C(n,k) = C(n-1,k)+C(n-1,k-1)得
C(n-1,0)+C(n,1)+...+C(n+m-1,m)
= C(n,0)+C(n,1)+C(n+1,2)+...+C(n+m-1,m)
= C(n+m,m)
【AC】

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 5 ll n,m,p; 6 7 ll fpow(ll x,ll n,ll p) 8 { 9 ll res=1; 10 while(n) 11 { 12 if(n&1) res=(res*x)%p; 13 x=(x*x)%p; 14 n>>=1; 15 } 16 return res; 17 } 18 ll Comb(ll n,ll m,ll p) 19 { 20 if(n<m) return 0; 21 if(n==m) return 1; 22 m=min(m,n-m); 23 ll lm=1,ln=1; 24 for(ll i=0;i<m;i++) 25 { 26 lm=(lm*(m-i))%p; 27 ln=(ln*(n-i))%p; 28 } 29 ll ans=ln*fpow(lm,p-2,p)%p; 30 return ans; 31 } 32 ll Lucas(ll n,ll m,ll p) 33 { 34 ll ans=1; 35 while(n&&m&&ans) 36 { 37 ans=(ans*Comb(n%p,m%p,p))%p; 38 n/=p; 39 m/=p; 40 } 41 return ans; 42 } 43 int main() 44 { 45 int T; 46 scanf("%d",&T); 47 while(T--) 48 { 49 scanf("%lld%lld%lld",&n,&m,&p); 50 n+=m; 51 ll ans=Lucas(n,m,p); 52 printf("%lld\n",ans); 53 } 54 return 0; 55 }

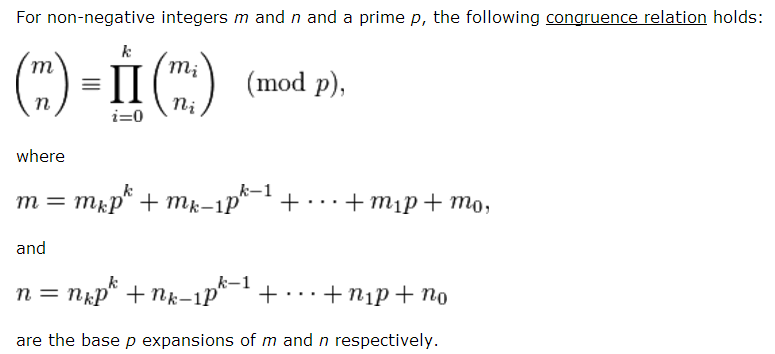


 浙公网安备 33010602011771号
浙公网安备 33010602011771号