【数学+枚举】OpenJ_POJ - C17J Pairs

https://vjudge.net/contest/171652#problem/J

【题意】

问有多少个正整数对(x,y)，使得存在正整数p,q满足

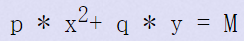
1 <= T <= 15

1 <= M <= 800,000

【思路】

  • M最多8e5，所以考虑枚举x,只有1e3个
  • 对于某个x,有多少对(x,y)其实就是看m-p*x*x有多少个不同的因子（需要去重）
  • 我们可以预处理1~8e5的每个数的所有因子（mlogm）
  • 分别枚举x,p,对所有m-p*x*x的因子去重，因为最大是因子8e5，所以可以开一个数组去重
  • 总的时间复杂度就是O(mlogm)+O(m*240)=O(mlogm)
  • m+m/4+m/9......是线性的，所有数的因子最多是240个左右

【Accepted】

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<string>
 5 #include<cmath>
 6 #include<algorithm>
 7 #include<queue>
 8 #include<set>
 9 #include<vector>
10 using namespace std;
11 typedef long long ll;
12 const ll mod=1e9+7;
13 const int maxn=8e5+3;
14 set<int> s[maxn];
15 set<int>::iterator it;
16 vector<int> v[maxn];
17 bool vis[maxn];
18 int n;
19 void init()
20 {
21     
22     for(int i=1;i<maxn;i++)
23     {
24         for(int j=i;j<maxn;j+=i)
25         {
26             v[j].push_back(i);
27          } 
28     }
29     int mmax=0;
30     for(int i=1;i<maxn;i++)
31     {
32         int sz=v[i].size();
33         mmax=max(mmax,sz);
34     }
35     cout<<mmax<<endl;
36 }
37 int main()
38 {
39     init();
40     int T;
41     scanf("%d",&T);
42     while(T--)
43     {
44         
45         scanf("%d",&n);    
46         int cnt=0;
47         for(int i=1;i<n;i++)
48         {
49             memset(vis,false,sizeof(vis));
50             int x=i*i;
51             if(x>=n) break;
52             for(int j=1;j<n;j++)
53             {
54                 if(x*j>=n) break;
55                 int y=n-x*j; 
56                 for(int k=0;k<v[y].size();k++)
57                 {
58                     if(!vis[v[y][k]])
59                     {
60                         vis[v[y][k]]=true;
61                         cnt++;
62                     }
63                 }
64             }
65         }
66         printf("%d\n",cnt);
67     }
68     return 0;
69 }
View Code

 【教训】

一开始T了是因为，为了去重所有容器都用了set,这样复杂度就带了logn

而vector的push_back是O(1)的

posted @ 2017-07-22 17:31  shulin15  阅读(396)  评论(0)  编辑  收藏  举报