算法渐进时间复杂度的比较

算法渐进时间复杂度的比较与可接受范围

在学习数据结构的第一章节中，我们经常会遇到一个关于算法渐进时间复杂度的比较结论：

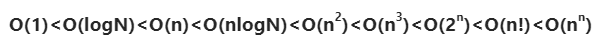
这个结论描述了不同时间复杂度函数在 ( N ) 趋于无穷大时的增长速率。本文将探讨这些时间复杂度的可接受范围，并解释哪些复杂度在实际应用中是可以接受的。

1. ( O(1) ) - 常数时间复杂度

常数时间复杂度 ( O(1) ) 表示无论输入规模 ( N ) 多大，算法的时间复杂度都是常数。这种复杂度是最理想的，因为它不受输入规模的影响。例如，访问数组中的一个元素、简单的算术运算等。

可接受性： 完全可接受。

2. ( O(\log N) ) - 对数时间复杂度

对数时间复杂度 ( O(\log N) ) 表示随着输入规模 ( N ) 增大，算法的时间复杂度以对数速率增长。这种复杂度通常出现在分治算法中，如二分查找。

可接受性： 完全可接受。

3. ( O(N) ) - 线性时间复杂度

线性时间复杂度 ( O(N) ) 表示算法的时间复杂度与输入规模 ( N ) 成正比。例如，遍历一个数组、线性查找等。

可接受性： 完全可接受。

4. ( O(N \log N) ) - 线性对数时间复杂度

线性对数时间复杂度 ( O(N \log N) ) 表示算法的时间复杂度介于线性和平方之间。这种复杂度通常出现在高效的排序算法中，如快速排序、归并排序。

可接受性： 完全可接受。

5. ( O(N^2) ) - 平方时间复杂度

平方时间复杂度 ( O(N^2) ) 表示算法的时间复杂度与输入规模 ( N ) 的平方成正比。例如，嵌套循环、简单的排序算法（如冒泡排序、选择排序）等。

可接受性： 在输入规模较小的情况下可接受，但在大规模数据处理中可能会变得不可接受。

6. ( O(N^3) ) - 立方时间复杂度

立方时间复杂度 ( O(N^3) ) 表示算法的时间复杂度与输入规模 ( N ) 的立方成正比。例如，某些矩阵运算、三重嵌套循环等。

可接受性： 在输入规模较小的情况下可接受，但在大规模数据处理中通常不可接受。

7. ( O(2^N) ) - 指数时间复杂度

指数时间复杂度 ( O(2^N) ) 表示算法的时间复杂度随输入规模 ( N ) 呈指数增长。例如，穷举法、某些组合问题等。

可接受性： 通常不可接受，除非输入规模非常小。

8. ( O(N!) ) - 阶乘时间复杂度

阶乘时间复杂度 ( O(N!) ) 表示算法的时间复杂度随输入规模 ( N ) 呈阶乘增长。例如，全排列问题、旅行商问题等。

可接受性： 通常不可接受，除非输入规模非常小。

9. ( O(N^N) ) - 超指数时间复杂度

超指数时间复杂度 ( O(N^N) ) 表示算法的时间复杂度随输入规模 ( N ) 呈超指数增长。这种复杂度通常出现在某些极端情况下。

可接受性： 通常不可接受，除非输入规模非常小。

总结

在实际应用中，算法的时间复杂度直接影响系统的性能和可扩展性。以下是一些常见的时间复杂度及其可接受范围：

• 完全可接受： ( O(1) )、( O(\log N) )、( O(N) )、( O(N \log N) )
• 在输入规模较小的情况下可接受： ( O(N^2) )、( O(N^3) )
• 通常不可接受： ( O(2^N) )、( O(N!) )、( O(N^N) )

在设计和选择算法时，应尽量选择时间复杂度较低的算法，以确保系统在高负载下的性能和稳定性。