最大公共子序列 一维数组滚动求值
子序列形式化定义:
给定一个序列X=<x1,x2,x3,x4...,xm>,另一个序列Y=<y1,y2,y3y4...,yk>,若存在一个严格递增的X的下标序列<i1,i2,i3,...,ik>对所有的1,2,3,...,k,都满足x(ik)=yk,则称Y是X的子序列
比如Y=<B,C,D,B>是X=<A,B,C,B,D,A,B>的子序列
公共子序列定义:
如果Z既是X的子序列,又是Y的子序列,则称Z为X和Y的公共子序列
最长公共子序列问题的结构及规划方程(二维数组):
设X=<x1,x2,x3,x4...,xm>,Y=<y1,y2,y3,y4...,yn>为两个序列,Z=<z1,z2,z3,z4...,zk>是他们的任意公共子序列
经过分析,我们可以知道:
1、如果xm = yn,则zk = xm = yn 且 Zk-1是Xm-1和Yn-1的一个LCS
2、如果xm != yn 且 zk != xm,则Z是Xm-1和Yn的一个LCS
3、如果xm != yn 且 zk != yn,则Z是Xm和Yn-1的一个LCS
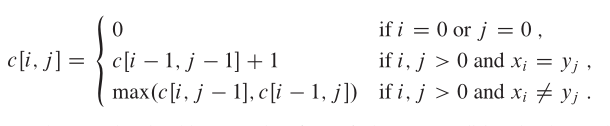
对于一维数组滚动求最长公共子序列分析:
我们可以从上述看出,当使用二维数组存放最优值数据是会浪费大量的空间,有许多值只用此次
从上述分析,不难发现可以用一维数组存值

不难发现,相等时他的更新值是”前一个值未更新时的值+1“,则可以用一个变量”tempO“存放旧值
变量”temp“则一直为”位置i-1“的值
完整代码:
1 /* 2 Problem:最长公共子序列--> 一维数组
Author:ItCod 3 */ 4 5 #include <iostream> 6 #include <stdlib.h> 7 #include <string> 8 9 using namespace std; 10 11 int lpsO(string m1, string m2) 12 { 13 int lm1 = m1.length(); 14 int lm2 = m2.length(); 15 int *set = (int *)malloc(lm2 + 1); 16 int temp = 0; // 作为中间变量 -->比较值 17 int tempO = 0; 18 19 for (int i = 0; i < lm2 + 1; i++) 20 set[i] = 0; // 初始化最优值数组set 21 22 for (int i = 0; i < lm1; i++) 23 { 24 tempO = set[0]; 25 for (int j = 1; j < lm2 + 1; j++) 26 { 27 temp = set[j - 1]; 28 if (m1[i] != m2[j - 1]) 29 { 30 tempO = set[j]; 31 if (temp >= set[j]) 32 { 33 set[j] = temp; 34 } 35 } 36 else 37 { 38 int f = set[j]; 39 set[j] = tempO + 1; // 如果相同,则获取前一个段的最优值 +1 40 tempO = f; 41 } 42 } 43 /* st1当前str[i] 比较后 set的状态
cout << i << ": "; 44 for (int i = 0; i < lm2 + 1; i++) 45 cout << set[i] << ends; 46 cout << endl;*/ 47 } 48 return set[lm2]; 49 } 50 51 int main() 52 { 53 string m1, m2; 54 cin >> m1 >> m2; 55 cout << "Longgest Public subSequence of length is : " << lpsO(m1, m2) << endl; 56 system("pause"); 57 return 0; 58 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号