红黑树其实很简单
1、背景
在开发过程中免不了需要维护一组数据,并且要能够快速地进行增删改查。如果数据量很大并且需要持久化,那么就选择数据库。但如果数据量相对少一些不需要持久化并且对响应时间要求很高,那么直接存储在本地内存中就最合适了。
2、链表
将数据存储在本地内存也不是随便存的,需要按不同的场景选择合适的数据结构。我们先来看下面这一组数据,54、24、74、12、42、62、83、9、17、33、49、58、65、79、90、5、20、29、37、46、69、86、95,需要选用一个数据结构存储它们,并且要能支持快速的增删改查操作。
说起数据结构,一般人第一反应就是最简单的线性结构,比如说数组、链表、栈或者队列等。如果有某一个场景可以使用下标随机访问数据,那么毫无疑问数组是最合适的,毕竟是直接通过内存地址(指针)访问数据,性能杠杠的。但实际开发中绝大多数场景都不可能提供下标访问数据,所以这里我们就先使用一个双向链表来看一下:

双向链表实现起来比较简单,这里就直接上代码了(链表不是重点,所以就只展示java的代码,作为今天的开胃菜):
public class DoublyLinked<V> implements Iterable<E> { /*链表的头和尾结点,不存储数据只作为标记*/ private final Node first, last; /*链表长度*/ private int size; public DoublyLinked() { this.first = new Node(null, null, new Node()); (this.last = first.next).prev = first; } /*链表中节点*/ class Node { V value; Node prev, next; public Node() {} public Node(V value, Node prev, Node next) { this.value = value; this.prev = prev; this.next = next; } } /*获取链表长度*/ public int size() { return size; } /*获取链表头结点节点*/ public V peekFirst() { Node node = first.next; return last == node ? null : node.value; } /*获取链表尾结点节点*/ public V peekLast() { Node node = last.prev; return first == node ? null : node.value; } /*向链表头部插入节点*/ public void addFirst(V value) { Node first = this.first; first.next = first.next.prev = new Node(value, first, first.next); ++size; } /*向链表尾部插入节点*/ public void addLast(V value) { Node last = this.last; last.prev = last.prev.next = new Node(value, last.prev, last); ++size; } /*删除链表头结点节点*/ public V removeFirst() { Node first = this.first, node = first.next; if (last != node) { (first.next = node.next).prev = first; node.prev = node.next = null; --size; } return node.value; } /*删除链表尾结点节点*/ public V removeLast() { Node last = this.last, node = last.prev; if (first != node) { (last.prev = node.prev).next = last; node.prev = node.next = null; --size; } return node.value; } /*查找链表中的节点*/ public boolean contains(V value) { for (Node node = first.next, last = this.last; last != node; node = node.next) { if (Objects.equals(value, node.value)) { return true; } } return false; } /*替换链表中的节点*/ public boolean replace(V source, V target) { for (Node node = first.next, last = this.last; last != node; node = node.next) { if (Objects.equals(source, node.value)) { node.value = target; return true; } } return false; } /*替换链表中的节点*/ public void replaceAll(V source, V target) { for (Node node = first.next, last = this.last; last != node; node = node.next) { if (Objects.equals(source, node.value)) { node.value = target; } } } /*删除链表中的节点*/ public boolean remove(V value) { for (Node prev = first, node = prev.next, last = this.last; last != node; node = (prev = node).next) { if (Objects.equals(value, node.value)) { (prev.next = node.next).prev = prev; node.prev = node.next = null; --size; return true; } } return false; } /*删除链表中的节点*/ public void removeAll(V value) { for (Node prev = first, node = prev.next, last = this.last; last != node; node = (prev = node).next) { if (Objects.equals(value, node.value)) { (prev.next = node.next).prev = prev; node.prev = node.next = null; node = prev; --size; } } } /*创建迭代器*/ @Override public Iterator<E> iterator() { return new Iterator<E>() { private Node current = DoublyLinked.this.first; @Override public boolean hasNext() { return DoublyLinked.this.last != current.next; } @Override public E next() { return (current = current.next).value; } }; } }
上面的链表中数据的是无序且可重复的,其中有关首尾节点操作的方法时间复杂度都为O(1),但同时这些操作能适用的范围也很窄。工作中大多数场景都是只知道具体的值然后操作链表,这时候更多的是使用contains、replace、remove等需要遍历链表中节点的方法,如果维护的是一个值有序或者值去重的链表,则插入节点的方法也需要遍历链表。如果每次遍历查找节点都是最坏情况,也就是每次查找的节点都在链表尾端,这时候时间复杂度就为O(n),其中n为链表的长度。在数据量少的情况下是没什么问题的,但是如果数据量很大链表很长,又遇到了高并发高吞吐量的场景,性能可能就不够看了。
3、二叉查找(排序)树
链表的操作弊端很明显,需要频繁遍历节点。但是遍历这个工作又是省不了的,那么可以想办法把需要遍历的路径变短,这时二叉查找(排序)树就很符合这个需求了。我们先来看一下二叉查找树的特点,首先其肯定是一棵二叉树,其次树中任意节点的关键字值一定大于其左子节点关键字值并且小于其右子节点关键字值,并且空树也是一棵二叉查找(排序)树。
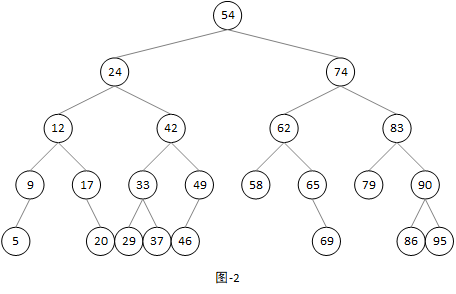
我们就以图2作为例子,讲解和演示二叉查找(排序)树的查找、插入和删除等操作。为了描述方便,后面我们称呼节点时,直接使用关键字值代替。
3.1、查找
假如我们需要查找关键字值为“37”的节点,那么操作步骤为:
1.首先将“37”与根节点的关键字值“54”进行比较,发现“37”比“54”小,所以继续与根节点左子节点的关键字值进行比较;
2.比较之后发现“37”比“24”大,所以继续与节点“24”的右子节点的关键字值进行比较;
3.比较之后发现“37”比“42”小,所以继续与节点“42”的左子节点的关键字值进行比较;
4.比较之后发现“37”比“33”大,所以继续与节点“33”的右子节点的关键字值进行比较;
5.比较之后发现相等,所以直接返回该节点;
这样查找数据不需要再遍历树中的所有节点,只需要沿着每个节点的一个子节点往下遍历就可以,大大缩短了查找路径。理想情况下时间复杂度变为了O(log n),其时间增长曲线为一个对数函数。
那么基于这样的逻辑,查找最大值和最小值是不是也很简单?这里就不多说了,大家自己试验一下。
3.2、插入
上面讲解了怎么查找节点,这里继续来看一下如何往树中插入一个节点。
假如我们插入关键字值为“52”的节点,那么操作步骤为:
1.首先将“52”与根节点的关键字值“54”进行比较,发现“52”比“54”小,所以继续与根节点左子节点的关键字值进行比较;
2.比较之后发现“52”比“24”大,所以继续与节点“24”的右子节点的关键字值进行比较;
3.比较之后发现“52”比“42”大,所以继续与节点“42”的右子节点的关键字值进行比较;
4.比较之后发现“52”比“49”大,所以继续与节点“49”的右子节点的关键字值进行比较;
5.这时发现节点“49”右子节点是空节点,所以直接将插入节点作为节点“49”的右子节点插入到树中;
如果在执行上面的步骤过程中,发现插入节点的关键字值与其中某一个节点的关键字值相等,则直接作为修改操作,不需要再插入结点。比如插入关键字值为“65”的节点,大家可以自己脑补一下插入的步骤。
3.3、删除
删除节点就比较麻烦一些,这里大概可以分为两种情况。一种是删除节点有两个子节点,一种是删除节点最多只有一个子节点。比如分别需要删除节点“65”、“29”、“24”三个节点,其中节点“65”有一个子节点,节点“29”没有子节点,节点“24”有两个子节点。
我们先看删除节点“65”的步骤:
1.首先需要找到关键字值为“65”的节点,怎么找就不需要再说一遍了吧;
2.直接移除节点“65”;
3.由于删除节点“65”是其父节点“62”的右子节点,所以需要将其右子节点“69”作为其父节点“62”的右子节点,重新建立父子关系;
删除节点“29”就更简单了,由于节点“29”没有子节点,所以通过值找到节点之后可以直接删除,不需要再建立父子关系。
至于删除节点“24”就比较麻烦了,由于其有两个子节点,如果将其移除之后两个子节点再与其父节点建立新的父子关系,那么就没有办法继续维持二叉查找树的结构了。这时就需要使用前继节点或者后继结点替换删除节点,作为新的删除节点被删除。
节点“24”的的前继节点为节点“20”,后继节点为节点“29”。大家看一下这三个节点之间都有什么关系?从值的大小来看,“20”是树中所有关键字值中比“24”小的最大值,“29”是比“24”大的最小值。从树的结构上来看,在水平衡轴上,节点“20”、“29”的两个节点是最靠近节点“24”的,也就意味着节点“24”的前继节点不可能有右子节点,后继结点不可能有左子节点。那么我们转换一下思路,假如将节点“24”移除之后,是否可以使用“20”、“29”这两个节点的其中一个填充到原节点“24”的位置上呢?最终删除节点“24”被转换为了删除节点“20”或者“29”了,问题是不是就解决了?至于如何查找前继节点和后继结点,这么简单的事情,在这里就不多说了,大家可以自试一下。
3.4、代码示例
由于二叉查找(排序)树并不是本文的重点,而且实现起来也很简单,所以这里就只是用java代码做演示。
public class BSTree<K extends Comparable<K>, V> { private Node root; private int size; /*获取树中节点个数*/ public int size() { return size; } /*获取根节点*/ public Entry<K, V> getRoot() { return null == root ? null : new Entry<>(root.key, root.value); } /*判断以给定节点为根节点的树是否为一棵二叉查找树*/ public boolean isBSTree(Node node) { // 如果当前节点为空,则从根节点开始递归校验 node = null == node ? root : node; if (null == node) { // 空树也是一棵二叉查找树 return true; } // 获取当前节点的父节点、左子节点、右子节点 Node parent = node.parent, nodeLeft = node.left, nodeRight = node.right; if (null != parent && parent.left != node && parent.right != node) { // 父节不为空,但是父节点的左右子节点引用都没有指向当前节点,所以不是一棵二叉树 return false; } if (null != nodeLeft) { // 当前节点的左子节点不为空 if (nodeLeft.parent != node || nodeLeft.compareTo(node) >= 0) { // 左子节点父节点引用没有指向当前节点,不满足是一棵二叉树。 // 或者左子节点的key值大于等于当前节点的key值,不满足是一棵二叉查找树(当前节点的key值大于左子节点小于右子节点) return false; } if (!isBSTree(nodeLeft)) { // 递归左子节点,判断子树是否满足红黑树特性 return false; } } if (null != nodeRight) { // 当前节点的右子节点不为空 if (nodeRight.parent != node || nodeRight.compareTo(node) <= 0) { return false; } if (!isBSTree(nodeRight)) { return false; } } return true; } /*根据key查找value*/ public V find(K key) { if (null == key) { throw new NullPointerException(); } Node node = findNode(key, root); return null == node ? null : node.value; } /*查找Key值最小的节点*/ public Entry<K, V> findMin() { Node node = root; while (null != node && null != node.left) { node = node.left; } return null == node ? null : new Entry<>(node.key, node.value); } /*查找Key值最大的节点*/ public Entry<K, V> findMax() { Node node = root; while (null != node && null != node.right) { node = node.right; } return null == node ? null : new Entry<>(node.key, node.value); } /*插入一个节点*/ public V put(K key, V value) { if (null == key) { throw new NullPointerException(); } Node current = root, parent = null; // 获取节点要插入的位置的父节点 int compare = 0; while (null != current && 0 != (compare = key.compareTo(current.key))) { current = compare > 0 ? (parent = current).right : (parent = current).left; } if (null != current) { // 要插入的key已存在 V ov = current.value; current.value = value; return ov; } if (null == parent) { // 要插入的树为空树 this.root = new Node(key, value, null); } else { // 插入新节点 if (compare < 0) { parent.left = new Node(key, value, parent); } else { parent.right = new Node(key, value, parent); } } ++size; return null; } /*删除节点*/ public V remove(K key) { if (null == key) { throw new NullPointerException(); } Node remove, replace; if (null == (remove = findNode(key, root))) { // 需要删除的节点在树中找不到 return null; } V value = remove.value; if (null != remove.left && null != (replace = remove.right)) { // 删除节点的左右子节点都不为空节点,将删除节点和后继节点替换(也可以使用前继节点替换删除节点) while (null != replace.left) { replace = replace.left; } remove.key = replace.key; remove.value = replace.value; remove = replace; } // 此时最多只有一个子节点 Node parent = remove.parent, child = null == (child = remove.left) ? remove.right : child; // 获取父节点和子节点 if (null != parent && null != child) { // 父节点不为空,并且有一个不为空的子节点 (parent.left == remove ? parent.left = child : (parent.right = child)).parent = parent; remove.parent = remove.left = null; } else if (null != parent) { // 父节点不为空,并且子节点都为空 remove.parent = parent.right == remove ? parent.right = null : (parent.left = null); } else if (null != child) { // 父节点为空,但是子节点不为空 root = child; remove.left = remove.right = child.parent = null; } else { // 父节点和子节点都为空 root = null; } --size; return value; } /*采用中序遍历二叉树,保证数据从小到大遍历*/ public void forEach(Consumer<Entry<K, V>> action) { Deque<Node> deque = new LinkedList<>(); for (Node node = root; node != null || !deque.isEmpty(); ) { for (; node != null; node = node.left) { deque.push(node); } Node pop = deque.pop(); action.accept(new Entry<>(pop.key, pop.value)); node = pop.right; } } /*通用查找节点*/ private Node findNode(K key, Node current) { Node found = null; for (int compare; null != current && null == found; ) { if ((compare = key.compareTo(current.key)) > 0) { current = current.right; } else if (compare < 0) { current = current.left; } else { found = current; } } return found; } class Node implements Comparable<Node> { K key; V value; Node parent, left, right; public Node(K key, V value, Node parent) { this.key = key; this.value = value; this.parent = parent; } @Override public int compareTo(Node node) { return key.compareTo(node.key); } } public static class Entry<K, V> { private final K key; private final V value; public Entry(K key, V value) { this.key = key; this.value = value; } public K getKey() { return key; } public V getValue() { return value; } @Override public String toString() { return "Entry{key=" + key + ", value=" + value + '}'; } } }
通过上面的分析,我们明白了二叉查找树的原理,其查找遍历节点路径的长度取决于树的高/深度。二叉树中任何节点下左右子树的高度差为节点的平衡因子,平衡因子越小树就越平衡(绝对平衡的平衡二叉树所有节点的平衡因子只会为-1、0、1),查找遍历节点所能体现出来的性能也就越好。
我们试想一下,如果图2中的数据事先就已经排好序了,然后依次插入二叉查找树中会有什么结果呢?假如数据是升序排列,那么插入树中的值会越来越大,结果就是数据只会一直往右子树中插入,最终树就会退化为一个链表,平衡因子就为树中节点的数量。删除节点的时候也可能造成平衡因子不可预测的增长。
4、红黑树
由于二叉查找树在插入或者删除节点的时候,有可能平衡因子会变的很大,甚至会直接退化为链表。最典型的就是插入有序数据的时候问题会很严重,但是在实际生产过程中,我们并不能避免插入的数据是有序的,这样又会破坏树的平衡性,所以就得想办法在插入或者删除节点之后对树的平衡进行调整。能满足这种特性的二叉树我们称其为自平横二叉树,目前业内已经存在很多很成熟的自平横二叉查找树。
现在常用到的自平横二叉查找树大概有6中,分别为堆树(Treap)、大小平衡树(SBT)、伸展树(Splay)、AVL树(平衡二叉查找树)、红黑树(Red-Black)、替罪羊树(Scapegoat)等。他们有的是通过节点旋转,有的是通过局部节点重组等操作进行自平横。今天我们要介绍的当然就是这其中最亮的那个仔平衡树中的扛把子 红黑树 。
我们来看一下红黑树的特性,首先其肯定是一棵二叉查找树,其次为了保持平衡其主要有以下5个特点:
- 每个节点的颜色是红色或者黑色;
- 根节点颜色是黑色;
- 每个叶子结点的颜色都是黑色(这里的叶子节点是指不存在的空节点);
- 红色节点的子节点都必须是黑色的(所有路径中不允许出现连续的两个红色节点);
- 任意节点到其叶子结点的所有路径上黑色节点的个数是相等的;
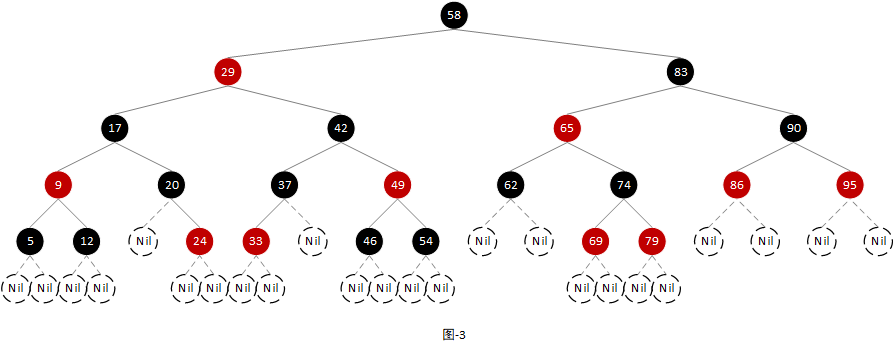
红黑树和AVL树不一样,它并没有显式地声明其平衡因子的范围,但是通过其5个特性却隐式地保证了树中任意节点的左右子树高度差绝对不会超过一倍,所以红黑树是一棵近似平衡的二叉查找树。那么说道这一点,红黑树只是近似平衡,和AVL树这种绝对平衡(任意节点左右子树高度差绝对值不大于1)的树相比,它凭什么更有优势呢?答案就在自平衡的操作上。基于上面的5点特性,红黑树在自平衡的时候能尽可能少的处理更多的节点,并且其时间复杂度相对更加稳定。所以目前各领域中红黑树应用的相对较多,比如jdk中的HashMap(jdk1.8及以上版本)、TreeMap,STL中的map、set,Linux系统中的epoll等。
上面讲解了链表、二叉查找树等,其实都只是作为抛砖引玉的作用,现在我们就要开始真正进入主题,详细分析一下红黑树了。由于后面后的逻辑分析会有很多红黑树的局部子树图,所以这里先声明一下图中各种形状节点的含义:

4.1、节点旋转
红黑树是通过节点的左右旋转或者改变节点颜色进行自平横的。改变节点节点颜色很好理解,在代码里面无非就是一个属性而已,这里就重点说一下旋转。
节点旋转分为左旋转和又旋转:
- 左旋转:以旋转结点作为支点,旋转节点的右子结点变为旋转结点的父结点,右子结点的左子结点变为旋转结点的右子结点,旋转节点的左子结点保持不变。如图4:
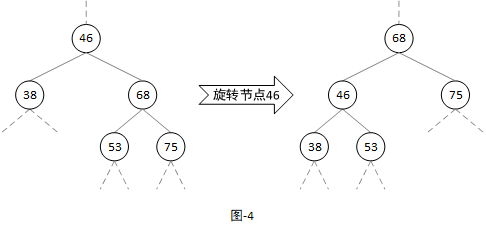
- 右旋转:以旋转结点作为支点,旋转结点的左子结点变为旋转结点的父结点,左子结点的右子结点变为旋转结点的左子结点,旋转结点的右子结点保持不变。如图5:

大家可以看一下,树被旋转前后的变化。可以发现其依然能够维持是一棵二叉查找树的结构,并且又能够调节部分节点的结构和左右子树的高度。所以通过旋转节点和改变节点的颜色,就能够将一棵不平衡的红黑树(不满足红黑树5个特性的树)调整成为一棵标准的红黑树。下面就开始分析在插入和删除节点之后,如何让破坏了平衡性的红黑树进行自平横。
4.2、插入操作
前面讲解红黑树特性的地方已经说道红黑树也是一棵二叉查找树,只不过其在插入节点之后需要做自平横操作(节点旋转或者颜色改变)。所以由此可知,在插入结点的时候红黑树和二叉查的操作是一样的,也就是先找到节点应该插入到什么位置(父节点的位置),如果在查找遍历过程中发现值已存在就做修改,如果不存在就插入。节点插入之后可能就会破坏树的平衡(不符合红黑树5大特性),下面我们就做自平横操作的分析。
首先,大家要记住一点,在你准备插入一个节点之前,红黑树一定是满足上面那5大特性的,在往树中插入了一个节点之后就有可能不满足了。
初始节点默认设置为红色节点,为了后面方便描述,在这里我们统一称插入节点为“当前节点”。在一棵标准的红黑树中插入一个节点之后,则会产生如下4个需要自平横的场景:
- 场景1:当前结点的父节点为空节点(父节点为根节点)
平衡操作为,直接将当前节点颜色设置为黑色,然后结束平衡操作。
- 场景2:当前节点的父节点为黑色节点
由于前节点为插入节点且其父节点是黑色节点,所以其左右子节点都为叶子节点,其兄弟节点既可以是红色节点也可以是叶子节点。如下图:
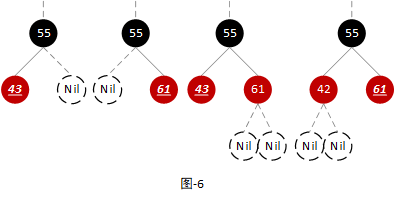
注:其中下划线标注的节点为当前节点。
由于向黑色节点下插入一个红色子节点不会破坏红黑树的平衡,所以可以直接结束平衡操作。
注:在后面的【场景4】中,当前节点不是插入节点时,还会衍生出另一种情况。当前节点的左右子节点为黑色节点,兄弟节点既可以是红色节点也可以是黑色节。但不论兄弟节点为什么节点,这两种情况都可以适配成【场景2】。
- 场景3:当前结点的父节点是红色节点,并且其叔叔节点不是红色节点
由于当前节点的父节点是红色节点,所以其祖父节点为黑色节点。由于当前节点为插入结点且叔叔节点不为红色节点,所以其左右子节点、叔叔节点等都是叶子节点。如下图:
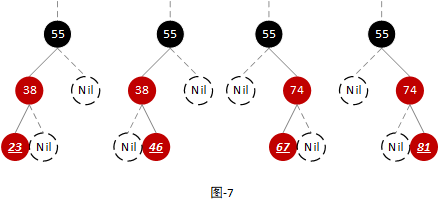
注:其中下划线标注的节点为当前节点。
我们以上图中第一颗树为例,进行平衡操作。首先将当前节点父节点的颜色置黑并且将祖父节点的颜色置红,然后以祖父节点为支点进行右旋转,再然后结束平衡操作。如下图:
我们再来看上图中第二棵树的平衡操作。首先将当前节点的父节点设为当前节点,然后以当前节点为支点进行左旋转。如下图:
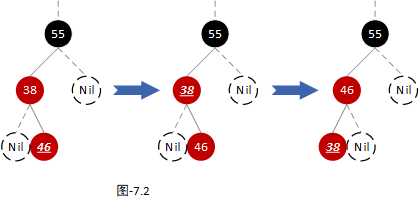
那么是不是就变成了和第一棵树一样的结构了,其他的就不用再多说了吧?
注:在后面的【场景4】中,当前节点不是插入节点时,还会衍生出另一种情况。当前节点的左右子节点、兄弟节点都为黑色节点。但不论如何,这两种情况都可以适配成【场景3】。
- 场景4:当前节点的父节点是红色节点,并且其叔叔节点也是红色节点
由于当前节点的父节点为红色节点,所以其祖父节点为黑色节点。由于当前节点是插入节点且叔叔节点为红色节点,所以其左右子节点、兄弟节点、叔叔节点的左右子节点都为叶子节点。如下图:

注:其中下划线标注的节点为当前节点
我们以上图中第一树为例,进行平衡操作。首先将当前节点的父节点和叔叔节点颜色置黑,然后将祖父节点的颜色置红,再然后将祖父节点设置为当前节点。如下图:
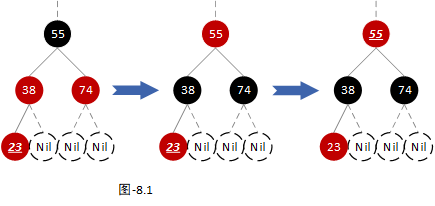
注:在下面的衍生场景中,当前节点不是插入节点时,还会衍生出另一种情况。当前节点的左右子节点、兄弟节点、叔叔节点的左右子节点都为黑色节点。但是不论如何,这两种情况都可以适配成【场景4】。
大家不要以为这样就结束了,我们还得继续看当前节点的父节点的类型。由此又可以衍生出下面4中情况:
- 当前节点的祖父节点为空节点,可适配【场景1】
- 当前节点的父节点为黑色节点,可适配【场景2】。如下图:
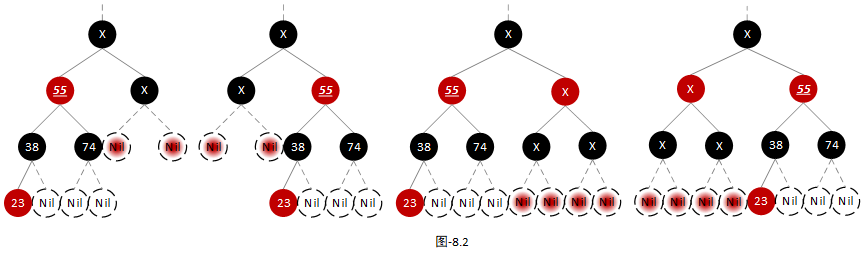
注:其中下划线标注的节点为当前节点。
- 当前节点的父节点是红色节点,并且其叔叔节点是黑色节点,可适配【场景3】。如下图:

注:其中下划线标注的节点为当前节点。
- 当前节点的父节点和叔叔节点都为红色节点,并且其兄弟节点和其叔叔节点的左右子节点都为黑色节点,可适配【场景4】。如下图:
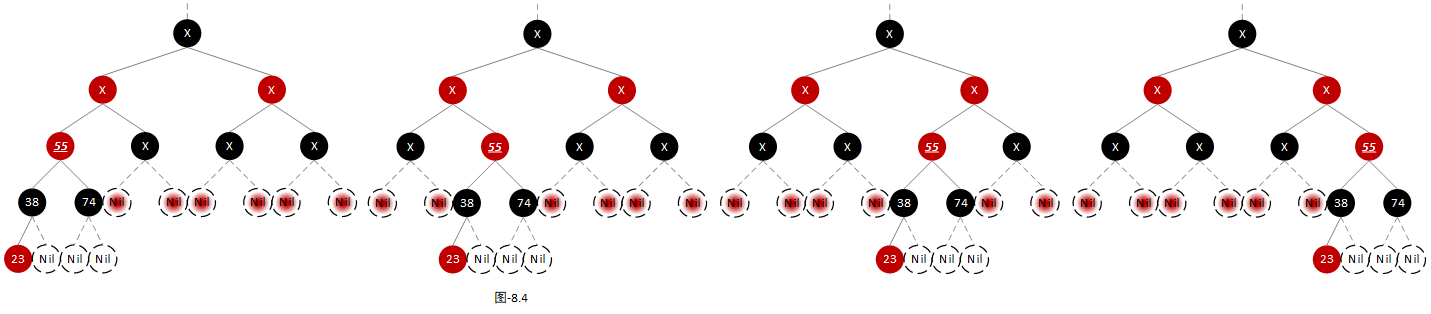
注:其中下划线标注的节点为当前节点。
插入总结:平衡的过程是一个循环,如果在当前节点和其父节点上处理过后还无法使树平衡,就需要将祖父节点设为当前节点并进入下一个循环处理。我们看【场景1】中当前节点的父节点为根节点、【场景2】中当前节点的父节点为黑色节点,都不需要再旋转或者改变节点颜色,树已经是平衡状态了。而【场景3】、【场景4】中经过多次循环旋转和变色处理将树平衡过后,我们发现当前节点的父节点要么是根节点要么就是黑色节点。所以我们总结,当父节点为根节点或者父节点为黑色节点时,树就已经平衡了。所以大家就明白为什么初始插入几节点默认是红色的了吧。
可能大家单看上面的场景分析还是不甚明白。但是没关系,说了这么多,最终的目的是要在代码层面去实现的,大家结合上面的场景分析然后去阅读后面的代码示例才是最终目的。
4.3、删除操作
相对于上面的插入操作,红黑树的删除操作相对来说会复杂一些,其实也就是需要自平横操作的场景会稍多一些。和插入一样,红黑树的节点删除操作也是和二叉查找树一样。首先要找到需要删除的节点,如果找不到就结束,如果找到了就看子节点情况。如果有两个非叶子节点的子节点,则使用前/后继结点替换删除节点。如果只有一个非叶子结点的子节点(该子节点下的两个子节点一定都是叶子节点),则使用该子节点作为前/后继结点替换删除节点。那么最终删除节点就只有两个叶子结点。
这时要注意,我们还不能直接就把需要删除的节点移出,因为删除节点需要参与到删除之前的平衡操作,平衡之后才能将节点删除。这里要说明一点,删除操作之前进行自平横平的目的,是要让删除节点变成树中多余的节点。也就是说平衡之后,剔除了删除节点的红黑树还能保持平衡,反之如果没有剔除树就不平衡了。
为了后面方便描述,在这里我们统一称删除节点为“当前节点”,在删除节点之前我们有4个需要平衡的场景:
- 场景1:当前节点的父节点为空节点(当前节点为根节点)
直接结束平衡操作,然后将需要删除的节点删除。
- 场景2:当前节点是红色节点
由于当前节点是红色节点,所以当前节点的父节点为黑色节点。由于当前节点为删除节点,所以其左右子节点为叶子节点,其兄弟节点既可以是红色节点也可以是叶子节点。如下图:

注:其中下划线标注的节点为当前节点。
我们以上图中第一颗树为例,进行平衡操作。在这里当前节点为红色节点,可以直接将当前节点颜色置黑,然后结束平衡操作,最后将需要删除的节点删除即可。如下图:
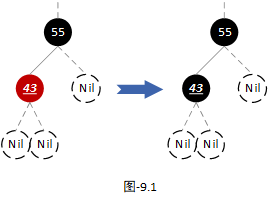
可能有人觉得,既然将当前节点删除不会破坏树的平衡,那么直接做删除操作不就行了,将当前节点的颜色置黑是不是就是多余的操作呢?在这里这一步操作并不多余,而且很重要,大家可以继续往后面看。
注:在后面的【场景5】中,当前节点不是删除节点时,还会衍生出另一种情况。当前节点的左右子节点为黑色节点,其兄弟节点既可以是红色节点也可以是黑色节点。但不论如何,这两种情况都可以适配成【场景2】。
- 场景3:当前节点和其兄弟节点都是黑色节点,并且其兄弟节点至少有一个红色子节点
由于当前节点和其兄弟节点都是黑色节点,所以当前节点的父节点既可以是红色节点也可以是黑色节点。由于前节点为删除节点并且其兄弟节点至少有一个红色节点,所以其左右子节点为叶子节点,其兄弟节点要么有一个红色子节点和一个叶子节点,要么有两个红色子节点。如下图:
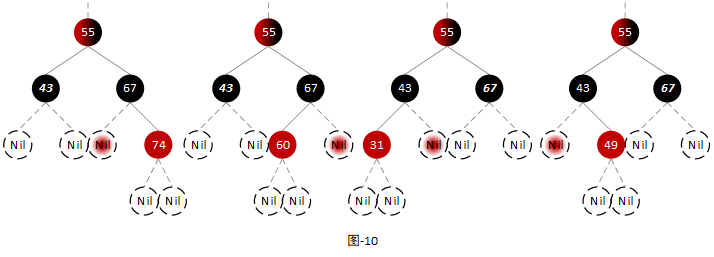
注:其中下划线标注的节点为当前节点。
我们以上图中第一颗树为例,进行平衡操作。首先将兄弟节点颜色变为父节点的颜色,然后将父节点和兄弟节点的右子节点的颜色置黑,再然后以父节点为支点进行左旋转。如下图:
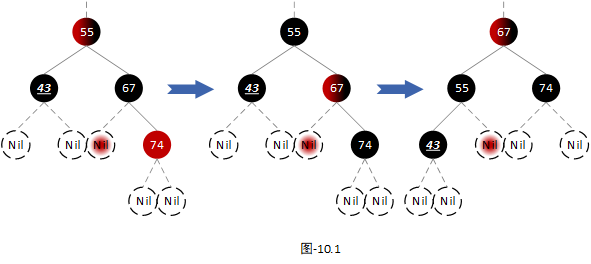
我们发现树已经是平衡的,这里做完操作之后就可以结束平衡,然后将需要删除的节点删除就可以了。
我们再来看上图中第二棵树的平衡操作。首先将兄弟节点颜色置红,并且将兄弟节点的左子节点颜色置黑,然后以兄弟节点为支点进行右旋转。如下图:
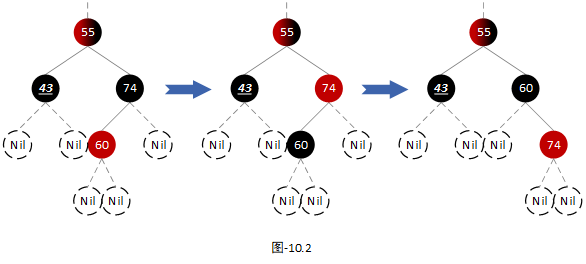
那么是不是就变成了和第一棵树一样的结构了,其他的就不用再多说了吧?
注:在后面的【场景5】中,当前节点不是删除节点时,还会衍生出另一种情况。当前节点的左右子节点不为叶子节点,其兄弟节点要么有一个红色节点一个黑色节点,要么有两个红色节点。但不论如何,这两种情况都可以适配成【场景3】。
- 场景4:当前节点为黑色节点,其兄弟节点为红色节点
由于当前节点的兄弟节点为红色节点,所以其父节点为黑色节点,其兄弟节点的左右子节点为黑色节点。由于当前节点为删节点并且是黑色节点,所以其左右子节点为叶子节点。如下图:
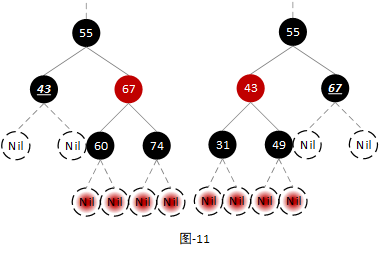
注:其中下划线标注的节点为当前节点。
我们以上图中第一颗树为例,进行平衡操作。首先将兄弟节点颜色置黑,同时将父节点颜色置红,然后以父节点为支点进行左旋转。如下图:
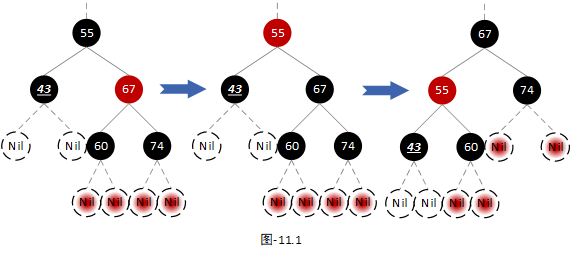
大家看上图,这么处理之后其实树还没有平衡,需要删除的节点还不能删除。但是当前场景处理到这里就已经结束了,剩下的平衡工作需要交给其他场景进行处理:
1.如果节点“60”下的两个子节点中至少有一个红色节点,则使用【场景3】的平衡处理方式;
2.如果节点“60”下的两个子节点都为叶子节点,则使用【场景5】的平衡方式处理;
注:在后面的【场景5】中,当前节点不是删除节点时,还会衍生出另一种情况。当前节点的左右子节点不为叶子节点,节点“60”下有两个黑色子节点,这种情况可以适配上【场景5】中衍生出来的场景。
- 场景5:当前节点和其兄弟节点都为黑色节点,并且其兄弟节点下没有红色子节点
由于当前节点和其兄弟节点都是黑色节点,所以当前节点的父节点既可以是红色节点也可以是黑色节点。由于前节点为删除节点且其兄弟节点没有子节点,所以当前节点和其兄弟节点的左右子节点都为叶子节点。如下图:
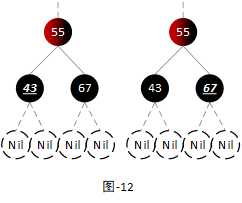
注:其中下划线标注的节点为当前节点。
我们以上图中第一颗树为例,进行平衡操作。首先将兄弟节点颜色置红,然后将父节点设为当前节点。如下图:
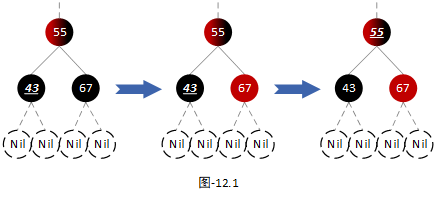
注:在下面的衍生场景中,当前节点不是插入节点时,还会衍生出另一种情况。当前节点的左右子节点不为叶子节点,兄弟节点的左右子节点都为黑色节点。但是不论如何,这两种情况都可以适配成【场景5】。
大家不要以为这样就结束了,我们还得继续看当前节点的兄弟节点的类型。由此又可以衍生出下面5中情况:
- 当前节点的父节点为空节点,可适配【场景1】
- 当前是红色节点,可以适配【场景2】。如下图:
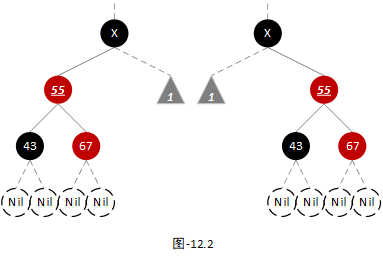
注:其中下划线标注的节点为当前节点
- 当前节点和其兄弟节点都是黑色节点,并且其兄弟节点有一个红色子节点,可适配【场景3】。如下图:

注:其中下划线标注的节点为当前节点
- 当前节点为黑色节点,其兄弟节点为红色节点,可适配【场景4】。如下图:
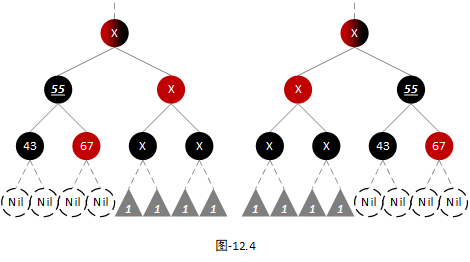
注:其中下划线标注的节点为当前节点
- 当前节点和其兄弟节点都为黑色节点,并且其兄弟节点有两个黑色子节点,可适配【场景5】。如下图:

注:其中下划线标注的节点为当前节点
删除总结:和插入平衡的过程一样,删除平衡也是一个循环处理的过程。如果在当前节点和其兄弟节点上处理过后还无法使树平衡,就需要将其父节点设为当前节点并进入下一个循环处理。再看【场景1】中当前节点为根节点、【场景2】中当前节点为红色节点、【场景3】的平衡处理之后,都不需要再次旋转或者改变节点颜色,树已经是平衡状态了。而【场景4】、【场景5】中经过多次循环旋转和变色处理将树平衡之后,发现当前节点要么是根节点要么就是红色节点,或者是【场景3】处理之后的结果。所以总结,当前节点为根节点或者为黑色节点再或者是【场景3】处理之后的结果时,树就已经平衡了。所以大家就明白【场景2】中为什么要将当前节点设为黑色节点了吧。
如果大家单看上面还是很晕乎,没关系,我们接下来就直接上代码了,大家对着上面的插入和删除场景去理解代码可能就会清晰一些。
4.4、代码示例
- java代码示例:
public class RBTree<K extends Comparable<K>, V> { private final static int RED = 0, BLACK = 1; private Node root; private int size; /*获取根节点的key*/ public Entry<K, V> getRoot() { return null == root ? null : new Entry<>(root.key, root.value); } /*获取树中节点个数*/ public int size() { return size; } /*判断以给定节点为根节点的树是否为一颗红黑树*/ public boolean isRBTree(Node node) { // 如果当前节点为空,则从根节点开始递归校验 node = null == node ? root : node; if (null == node) { // 空树也是一棵红黑树 return true; } // 获取当前节点的父节点、左子节点、右子节点 Node parent = node.parent, nodeLeft = node.left, nodeRight = node.right; if (null != parent && parent.left != node && parent.right != node) { // 父节不为空,但是父节点的左右子节点引用都没有指向当前节点,所以不是一颗二叉树 return false; } if (null != nodeLeft) { // 当前节点的左子节点不为空 if (nodeLeft.parent != node || nodeLeft.compareTo(node) >= 0) { // 左子节点父节点引用没有指向当前节点,不满足是一颗二叉树。 // 或者左子节点的key值大于等于当前节点的key值,不满足是一颗二叉查找树(当前节点的key值大于左子节点小于右子节点) return false; } if (RED == nodeLeft.color) { if (RED == node.color) { // 当前节点和当前节点的左子节点都红色节点,不满足是一颗红黑树(红黑树中的任何路径上都不能出现连续的两个红色节点) return false; } } else { if (null == nodeRight) { // 左子节点为黑色节点右子节点为空节点,不满足是一个红黑树(从一个节点到它所能到达的任何叶子结点的任何路径上黑色结点个数必须相等) return false; } else if (RED == nodeRight.color && (null == nodeRight.left || null == nodeRight.right)) { // 左子节点为黑色,右子节点为红色并且其子节点有一个为Nil节点,不满足是一颗红黑树(从一个节点到它所能到达的任何叶子结点的任何路径上黑色结点个数必须相等) return false; } } if (!isRBTree(nodeLeft)) { // 递归左子节点,判断子树是否满足红黑树特性 return false; } } if (null != nodeRight) { // 当前节点的右子节点不为空 if (nodeRight.parent != node || nodeRight.compareTo(node) <= 0) { return false; } if (RED == nodeRight.color) { if (RED == node.color) { return false; } } else { if (null == nodeLeft) { return false; } else if (RED == nodeLeft.color && (null == nodeLeft.left || null == nodeLeft.right)) { return false; } } if (!isRBTree(nodeRight)) { return false; } } return true; } /*根据key查找value*/ public V find(K key) { if (null == key) { throw new NullPointerException(); } Node node = findNode(key, root); return null == node ? null : node.value; } /*查找Key值最小的节点*/ public Entry<K, V> findMin() { Node node = root; while (null != node && null != node.left) { node = node.left; } return null == node ? null : new Entry<>(node.key, node.value); } /*查找Key值最大的节点*/ public Entry<K, V> findMax() { Node node = root; while (null != node && null != node.right) { node = node.right; } return null == node ? null : new Entry<>(node.key, node.value); } /*向红黑树中插入节点*/ public V put(K key, V value) { if (null == key) { throw new NullPointerException(); } Node current = root, parent = null; // 获取节点要插入的位置的父节点 int compare = 0; while (null != current && 0 != (compare = key.compareTo(current.key))) { current = compare > 0 ? (parent = current).right : (parent = current).left; } if (null != current) { // 要插入的key已存在 V ov = current.value; current.value = value; return ov; } if (null == parent) { // 要插入的树为空树 root = new Node(key, value, BLACK, null); } else { // 插入新节点 Node insert = new Node(key, value, RED, parent); current = compare < 0 ? parent.left = insert : (parent.right = insert); fixAfterPut(current); // 重新平衡插入节点后的树 } ++size; return null; } /*从红黑树中删除节点*/ public V remove(K key) { if (null == key) { throw new NullPointerException(); } Node remove, parent, replace; if (null == (remove = findNode(key, root))) { // 需要删除的节点在树中找不到 return null; } V value = remove.value; if (null != remove.left && null != (replace = remove.right)) { // 删除节点的左右子节点都不为空节点,将删除节点和后继节点替换 while (null != replace.left) { replace = replace.left; } remove.key = replace.key; remove.value = replace.value; remove = replace; } // 此时子节点最多只有一个非叶子节点 if (null != (null == (replace = remove.left) ? replace = remove.right : replace)) { // 删除节点的左右子节点有一个不为空,将删除节点和子节点替换 remove.key = replace.key; remove.value = replace.value; remove = replace; } // 此时子节点全部为叶子节点 if (null == (parent = remove.parent)) { // 删除节点为根节点 root = null; } else { fixBeforeRemove(remove); // 删除节点之前需要重新将树平衡 remove.parent = parent.right == remove ? parent.right = null : (parent.left = null); // 最后删除节点 } --size; return value; } /*采用中序遍历二叉树,保证数据从小到大遍历*/ public void forEach(Consumer<Entry<K, V>> action) { Deque<Node> deque = new LinkedList<>(); for (Node node = root; node != null || !deque.isEmpty(); ) { for (; node != null; node = node.left) { deque.push(node); } Node pop = deque.pop(); action.accept(new Entry<>(pop.key, pop.value)); node = pop.right; } } /*查找节点*/ private Node findNode(K key, Node current) { Node found = null; for (int compare; null != current && null == found; ) { if ((compare = key.compareTo(current.key)) > 0) { current = current.right; } else if (compare < 0) { current = current.left; } else { found = current; } } return found; } /*左旋转节点*/ private void rotateLeft(Node rotate) { // 获取旋转节点的右子节点 Node right, parent, broLeft; if (null == rotate || null == (right = rotate.right)) { return; } if (null != (broLeft = rotate.right = right.left)) { // 将旋转节点的右子节点设置为右子节点的左子节点,并将右子节点的左子节点父节点设置为旋转节点 broLeft.parent = rotate; } if (null == (parent = right.parent = rotate.parent)) { // 右子节点的父节点设置为旋转节点的父节点,如果父节点为空则将右子节点设置为根节点,并将颜色设置为黑色 (this.root = right).color = BLACK; } else if (parent.left == rotate) { parent.left = right; } else { parent.right = right; } right.left = rotate; rotate.parent = right; } /*右旋转节点*/ private void rotateRight(Node rotate) { // 获取旋转节点的左子节点 Node left, parent, broRight; if (null == rotate || null == (left = rotate.left)) { return; } if (null != (broRight = rotate.left = left.right)) { // 将旋转节点的左子节点设置为左子节点的右子节点,并将左子节点的右子节点父节点设置为旋转节点 broRight.parent = rotate; } if (null == (parent = left.parent = rotate.parent)) { // 将左子节点的父节点设置为旋转节点的父节点,如果父节点为空则将左子节点设置为根节点,并将颜色置黑 (this.root = left).color = BLACK; } else if (parent.left == rotate) { parent.left = left; } else { parent.right = left; } left.right = rotate; rotate.parent = left; } /*插入数据之后将树进行平衡*/ private void fixAfterPut(Node current) { for (Node parent, grandfather, graLeft, graRight; ; ) { if (null == (parent = current.parent)) { // TODO: 当前节点父节点是空节点,适配【场景1】 current.color = BLACK; break; } if (BLACK == parent.color || null == (grandfather = parent.parent)) { // TODO: 当前节点的父节点是黑色节点,或者祖父节点是空节点(父节点是根节点),适配【场景2】 break; } if ((graLeft = grandfather.left) == parent) { // 父节点为祖父节点的左子节点 /* * 节点情况分析: * 1、当前节点不为空,并且为红色节点 * 2、当前节点的父节点不为空,并且为红色节点 * 3、当前节点的祖父节点不为空,并且为黑色节点 */ if (null != (graRight = grandfather.right) && RED == graRight.color) { // TODO: 当前节点的叔叔节点是红色节点,适配【场景4】 graRight.color = BLACK; // 将叔叔节点颜色置黑 parent.color = BLACK; // 将父节点颜色置黑 grandfather.color = RED; // 将祖父节点颜色置红 current = grandfather; // 将祖父节点设为当前节点 } else { // TODO: 当前节点的叔叔节点是叶子节点或者黑色节点,适配【场景3】 if (current == parent.right) { // 当前节点为父节点的右子节点 rotateLeft(current = parent); // 将将父节点设为当前节点并将当前节点左旋转 grandfather = (parent = current.parent).parent; // 重新为父节点和祖父节点赋值 } parent.color = BLACK; // 将父节点颜色置黑 grandfather.color = RED; // 将祖父节点颜色置红 rotateRight(grandfather); // 将祖父节点进行右旋转 } } else { // 父节点为祖父节点的右子节点,这里就不做注释了 if (null != graLeft && RED == graLeft.color) { graLeft.color = BLACK; parent.color = BLACK; grandfather.color = RED; current = grandfather; } else { if (current == parent.left) { rotateRight(current = parent); grandfather = (parent = current.parent).parent; } parent.color = BLACK; grandfather.color = RED; rotateLeft(grandfather); } } } } /*删除节点之前将数平衡*/ private void fixBeforeRemove(Node current) { for (Node parent, left, right; null != current // 当前节点不为空 && null != (parent = current.parent); ) { // TODO: 当前节点的父节点是空节点,适配【场景1】 if (RED == current.color) { // TODO: 当前节点为红色节点,适配【场景2】 current.color = BLACK; break; } if ((left = parent.left) == current) { // 如果当前节点为父节点的左子节点 /* * 节点情况分析: * 1、当前节点是黑色节点 * 2、当前节点的兄弟节点不是叶子结点 */ if (RED == (right = parent.right).color) { // TODO: 当前节点的兄弟节点为红色节点,适配【场景4】 /* * 节点情况分析: * 1、父节点为黑色节点; * 2、兄弟节点的左右子节点为黑色节点; */ right.color = BLACK; // 将兄弟节点颜色置黑 parent.color = RED; // 将父节点颜色置红 rotateLeft(parent); // 将父节点左旋转(当前节点任然是父节点的左子节点) right = parent.right; // 重新获取当前节点的兄弟节点 } /* * 节点情况分析: * 1、当前节点的兄弟节点一定为黑色节点 */ Node broLeft = right.left, broRight = right.right; if ((null == broRight || BLACK == broRight.color) && (null == broLeft || BLACK == broLeft.color)) { // TODO: 当前节点兄弟节点的左右子节点不存在红色节点,适配【场景5】 /* * 节点情况分析: * 情况1:当前节点兄弟节点的左右子节点都为黑色节点 * 情况2:当前节点兄弟节点的左右子节点都为叶子节点 */ right.color = RED; // 将兄弟节点颜色置红 current = parent; // 将父节点设为当前节点 } else { // TODO: 当前节点的兄弟节点至少有一个红色子节点,适配【场景3】 if (null == broRight || BLACK == broRight.color) { // 兄弟节点的右子节点为叶子节点或者黑色节点,则兄弟节点的左子节点一定为红色节点 broLeft.color = BLACK; // 将兄弟节点的左子节点颜色置黑 right.color = RED; // 将兄弟节点颜色置红 rotateRight(right); // 将兄弟节点右旋转 right = parent.right; // 重新获取右子节点 broRight = right.right; } right.color = parent.color; // 将兄弟节点的颜色置为父节点的颜色 broRight.color = BLACK; // 将兄弟节点的右子节点颜色置黑 parent.color = BLACK; // 将父节点颜色置黑 rotateLeft(parent); // 将父节点左旋转 break; } } else { // 当前节点为右子节点,这里就不做注释了 if (RED == left.color) { left.color = BLACK; parent.color = RED; rotateRight(parent); left = parent.left; } Node broLeft = left.left, broRight = left.right; if ((null == broLeft || BLACK == broLeft.color) && (null == broRight || BLACK == broRight.color)) { left.color = RED; current = parent; } else { if (null == broLeft || BLACK == broLeft.color) { broRight.color = BLACK; left.color = RED; rotateLeft(left); left = parent.left; broLeft = left.left; } left.color = parent.color; broLeft.color = BLACK; parent.color = BLACK; rotateRight(parent); break; } } } } class Node implements Comparable<Node> { K key; V value; int color; Node parent, left, right; public Node(K key, V value, int color, Node parent) { this.key = key; this.value = value; this.color = color; this.parent = parent; } @Override public int compareTo(Node node) { return key.compareTo(node.key); } } public static class Entry<K, V> { private final K key; private final V value; public Entry(K key, V value) { this.key = key; this.value = value; } public K getKey() { return key; } public V getValue() { return value; } @Override public String toString() { return "Entry{" + "key=" + key + ", value=" + value + '}'; } } }
- java代码测试用例:
public class RBTreeTest { @Test public void put() { ThreadLocalRandom random = ThreadLocalRandom.current(); RBTree<Integer, String> tree = new RBTree<>(); for (int i = 0; i < 100; ++i) { int key = (random.nextInt(100000) & Integer.MAX_VALUE) % 100; tree.put(key, String.valueOf(key)); } RBTree.Entry<Integer, String> root = tree.getRoot(); System.out.printf("rootKey=%d, rootValue=%s, size=%d, isRBTree=%b\n", root.getKey(), root.getValue(), tree.size(), tree.isRBTree(null)); } @Test public void remove() { ThreadLocalRandom random = ThreadLocalRandom.current(); RBTree<Integer, String> tree = new RBTree<>(); for (int i = 0; i < 100; ++i) { int key = (random.nextInt(100000) & Integer.MAX_VALUE) % 100; tree.put(key, String.valueOf(key)); } // while (tree.size() > 0) { tree.remove(tree.getRoot().getKey()); System.out.printf("size=%d, isRBTree=%b\n", tree.size(), tree.isRBTree(null)); } } @Test public void find() { ThreadLocalRandom random = ThreadLocalRandom.current(); RBTree<Integer, String> tree = new RBTree<>(); for (int i = 0; i < 100; ++i) { int key = (random.nextInt(100000) & Integer.MAX_VALUE) % 100; tree.put(key, String.valueOf(key)); } System.out.println(tree.find(random.nextInt(100000) % 100)); } @Test public void findMin() { ThreadLocalRandom random = ThreadLocalRandom.current(); RBTree<Integer, String> tree = new RBTree<>(); for (int i = 0; i < 100; ++i) { int key = (random.nextInt(100000) & Integer.MAX_VALUE) % 100; tree.put(key, String.valueOf(key)); } System.out.println(tree.findMin()); } @Test public void findMax() { ThreadLocalRandom random = ThreadLocalRandom.current(); RBTree<Integer, String> tree = new RBTree<>(); for (int i = 0; i < 100; ++i) { int key = (random.nextInt(100000) & Integer.MAX_VALUE) % 100; tree.put(key, String.valueOf(key)); } System.out.println(tree.findMax()); } @Test public void foreach() { ThreadLocalRandom random = ThreadLocalRandom.current(); RBTree<Integer, String> tree = new RBTree<>(); for (int i = 0; i < 100; ++i) { int key = (random.nextInt(100000) & Integer.MAX_VALUE) % 100; tree.put(key, String.valueOf(key)); } RBTree.Entry<Integer, String> root = tree.getRoot(); System.out.printf("rootKey=%d, rootValue=%s, size=%d, isBSTree=%b\n", root.getKey(), root.getValue(), tree.size(), tree.isRBTree(null)); System.out.println(tree.findMin().getValue() + " " + tree.findMax().getValue()); tree.forEach(System.out::println); } }
- C代码示例:
由于本人是做java开发的,C的语法和编码风格并不是很标准,所以大家就将就看一下
#define _CRT_SECURE_NO_WARNINGS #pragma once #include <stdlib.h> #include <stdio.h> #include <string.h> #ifdef __cplusplus extern "C" { #endif // __cplusplus /*红黑树节点*/ typedef struct _RBNode { void *p_key; // key可以是任意类型,key值比较器比较key的大小 void *p_value; // value也可以是任意类型 char color; // 0代表红色,非0代表黑色 struct _RBNode *p_parent, *p_left, *p_right; }RBNode; /*红黑树结构体*/ typedef struct _RBTree { int size; // 节点数量 RBNode *p_root; // 根节点指针 // 树中key值比较器,参数1:须必较的key值指针,参数2:须必交的key值指针,参数3:返回值指针 int(*p_kcmp)(void *, void *, char *); }RBTree; /* * 创建一棵空的红黑树; * 参数列表: * p_tree:红黑树指针; * Key_Comparator:代表key值比较器; * 返回值: * NULL:代表函数执行失败;!NULL:代表返回的红黑树指针; */ RBTree *create_RBTree(int(*p_kcmp)(void *, void *, char *)); /* * 判断以给定节点为根节点的树是否为一颗红黑树; * 参数列表: * p_tree:红黑树指针; * p_node:需要判断的起始节点指针,如果为空则取根节点; * p_res:判断结果,0:不是一颗红黑树;1:是一颗红黑树; * 返回值: * 0:代表函数执行失败;!0:代表函数执行成功; */ int is_RBTree(RBTree *p_tree, RBNode *p_node, char *p_res); /* * 在红黑树中查找节点 * 参数列表: * p_key:要查找的节点的key指针; * p_tree:要查找的红黑树的的指针; * p_res:查找到的值; * 返回值: * 0:代表函数执行失败;!0:代表函数执行成功; */ int find_RBTree(void *p_key, RBTree *p_tree, void **p_res); /* * 在红黑树中查找Key值最小的节点 * 参数列表: * p_tree:要查找的红黑树的的指针; * p_res:查找到的值; * 返回值: * 0:代表函数执行失败;!0:代表函数执行成功; */ int findMin_RBTree(RBTree *p_tree, RBNode **p_res); /* * 在红黑树中查找Key值最大的节点 * 参数列表: * p_tree:要查找的红黑树的的指针; * p_res:查找到的值; * 返回值: * 0:代表函数执行失败;!0:代表函数执行成功; */ int findMax_RBTree(RBTree *p_tree, RBNode **p_res); /* * 向红黑树中插入节点 * 参数列表: * p_key:要插入节点的key * p_value:要插入节点的value * p_tree:要插入节点的红黑树 * 返回值: * 0:代表函数执行失败;!0:代表函数执行成功; */ int put_RBTree(void *p_key, void *p_value, RBTree *p_tree); /* * 从红黑树中删除节点 * 参数列表: * p_key:要删除节点的key * p_tree:要删除节点的红黑树 * p_res:删除节点的value值指针,如果传入的是NULL,函数内部会释放这部分空间 * 返回值: * 0:代表函数执行失败;!0:代表函数执行成功; */ int remove_RBTree(void *p_key, RBTree *p_tree, void **p_res); /* * 释放红黑树 * 参数列表: * p_tree:需要释放的红黑树 */ void free_RBTree(RBTree *p_tree); #ifdef __cplusplus } #endif // __cplusplus
#include "RBTree.h" int findNode(int(*p_kcmp)(void *, void *, char *), void *p_key, RBNode *p_curr, RBNode **p_res); void rotateLeft(RBTree *p_tree, RBNode *p_rotate); void rotateRight(RBTree *p_tree, RBNode *p_rotate); void fixAfterPut(RBTree *p_tree, RBNode *p_current); void fixBeforeRemove(RBTree *p_tree, RBNode *p_current); RBTree *create_RBTree(int(*p_kcmp)(void *, void *, char *)) { if (!p_kcmp) // 如果key值比较器函数为空,则不能创建红黑树 return NULL; // 为红黑树开辟空间并初始化 RBTree *p_tree = NULL; size_t st_size = sizeof(RBTree); if (!(p_tree = (RBTree *)malloc(st_size))) return NULL; memset(p_tree, 0, st_size); p_tree->p_kcmp = p_kcmp; return p_tree; } int is_RBTree(RBTree *p_tree, RBNode *p_node, char *p_res) { if (!p_tree) // 要校验的红黑树不能为空 return 0; // 如果传入的要交验的节点为空,则从根节点开始校验,如果根节点也为空,则返回成功(空树也是一棵红黑树) if (!(p_node = !p_node ? p_tree->p_root : p_node)) return *p_res = 1; // 获取当前节点的父节点、左子节点、右子节点等指针 RBNode *p_parent = p_node->p_parent, *p_nodeL = p_node->p_left, *p_nodeR = p_node->p_right; // 如果父节不为空,但是父节点的左右子节点指针都没有指向当前节点,所以不是一颗二叉树 if (p_parent && p_parent->p_left != p_node && p_parent->p_right != p_node) return !(*p_res = 0); char compare = 0; if (p_nodeL) // 当前节点的左子节点不为空 { if (!p_tree->p_kcmp(p_nodeL->p_key, p_node->p_key, &compare)) // 比较左子节点的key和右子节点的key的大小 return 0; // 左子节点父节点引用没有指向当前节点,不满足是一颗二叉树。或者左子节点的key值大于等于当前节点的key值,不满足是一颗二叉查找树 if (p_nodeL->p_parent != p_node || compare >= 0) return !(*p_res = 0); if (!p_nodeL->color) { if (!p_node->color) // 当前节点和当前节点的左子节点都红色节点,不满足是一颗红黑树 return !(*p_res = 0); } else { if (!p_nodeR) // 左子节点为黑色节点右子节点为空节点,不满足是一个红黑树 return !(*p_res = 0); // 左子节点为黑色,右子节点为红色并且其子节点有一个为Nil节点,不满足是一颗红黑树 if (!p_nodeR->color && (!p_nodeR->p_left || !p_nodeR->p_right)) return !(*p_res = 0); } // 递归左子节点,判断子树是否满足红黑树特性 if (!is_RBTree(p_tree, p_nodeL, p_res)) return 0; else if (!*p_res) return 1; } if (p_nodeR) { // 当前节点的右子节点不为空 if (!p_tree->p_kcmp(p_nodeR->p_key, p_node->p_key, &compare)) return 0; if (p_nodeR->p_parent != p_node || compare <= 0) return !(*p_res = 0); if (!p_nodeR->color) { if (!p_node->color) return !(*p_res = 0); } else { if (!p_nodeL) return !(*p_res = 0); if (!p_nodeL->color && (!p_nodeL->p_left || !p_nodeL->p_right)) return !(*p_res = 0); } if (!is_RBTree(p_tree, p_nodeR, p_res)) return 0; else if (!*p_res) return 1; } return *p_res = 1; } int find_RBTree(void *p_key, RBTree *p_tree, void **p_res) { if (!p_key || !p_tree || !p_res) return 0; RBNode *p_node = NULL; if (!findNode(p_tree->p_kcmp, p_key, p_tree->p_root, &p_node)) // 判断查找节点函数是否执行失败 return 0; *p_res = !p_node ? NULL : p_node->p_value; return 1; } int findMin_RBTree(RBTree *p_tree, RBNode **p_res) { if (!p_tree || !p_res) return 0; RBNode *p_node = p_tree->p_root; while (p_node && p_node->p_left) p_node = p_node->p_left; *p_res = p_node; return 1; } int findMax_RBTree(RBTree *p_tree, RBNode **p_res) { if (!p_tree || !p_res) return 0; RBNode *p_node = p_tree->p_root; while (p_node && p_node->p_right) p_node = p_node->p_right; *p_res = p_node; return 1; } int put_RBTree(void *p_key, void *p_value, RBTree *p_tree, void **p_res) { if (!p_key || !p_tree) return 0; RBNode *p_parent = NULL, *p_curr = p_tree->p_root; // 获取节点要插入的位置的父节点 char compare = 0; while (p_curr) { if (!p_tree->p_kcmp(p_key, p_curr->p_key, &compare)) return 0; if (!compare) break; p_parent = p_curr; p_curr = compare > 0 ? p_curr->p_right : p_curr->p_left; } if (p_curr) // 要插入的key已存在 { if (p_curr->p_key && p_curr->p_key != p_key) free(p_curr->p_key); if (p_res) // 代表返回值的指针不为空,则表示需要将删除节点的value值传出去 *p_res = p_curr->p_value; else if (p_curr->p_value && p_curr->p_value != p_value) // 直接将节点的value值释放 free(p_curr->p_value); p_curr->p_key = p_key; p_curr->p_value = p_value; return 1; } // 开辟红黑树节点空间并初始化 RBNode *p_insert = NULL; size_t st_size = sizeof(RBNode); if (!(p_insert = (RBNode *)malloc(st_size))) return 0; memset(p_insert, 0, st_size); p_insert->p_key = p_key; p_insert->p_value = p_value; if (!(p_insert->p_parent = p_parent)) // 要插入节点的红黑树是空树 (p_tree->p_root = p_insert)->color = 1; else // 要插入节点的红黑树不是空树,直接将节点插入 { p_curr = compare < 0 ? p_parent->p_left = p_insert : (p_parent->p_right = p_insert); fixAfterPut(p_tree, p_curr); // 重新平衡插入节点后的树 } ++p_tree->size; return 1; } int remove_RBTree(void *p_key, RBTree *p_tree, void **p_res) { if (!p_key || !p_tree) return 0; RBNode *p_remove = NULL, *p_parent = NULL, *p_replace = NULL; if (!findNode(p_tree->p_kcmp, p_key, p_tree->p_root, &p_remove)) // 判断查找节点函数是否执行失败 return 0; if (!p_remove) // 如果没有查找到要删除的节点就直接返回 return 1; else if (p_res) // 代表返回值的指针不为空,则表示需要将删除节点的value值传出去 *p_res = p_remove->p_value; else if (p_remove->p_value) // 直接释放删除节点的value值 free(p_remove->p_value); p_remove->p_value = NULL; if (p_remove->p_left && (p_replace = p_remove->p_right)) { // 删除节点的左右子节点都不为空节点,将删除节点和后继节点替换 while (p_replace->p_left) p_replace = p_replace->p_left; void* temp = p_remove->p_key; p_remove->p_key = p_replace->p_key; p_replace->p_key = temp; p_remove->p_value = p_replace->p_value; p_replace->p_value = NULL; p_remove = p_replace; } // 此时子节点最多只有一个非叶子节点 if ((p_replace = !(p_replace = p_remove->p_left) ? p_remove->p_right : p_replace)) { // 删除节点的左右子节点有一个不为空,将删除节点和子节点替换 void* temp = p_remove->p_key; p_remove->p_key = p_replace->p_key; p_replace->p_key = temp; p_remove->p_value = p_replace->p_value; p_replace->p_value = NULL; p_remove = p_replace; } // 此时子节点全部为叶子节点 if (!(p_parent = p_remove->p_parent)) // 删除节点为根节点 p_tree->p_root = NULL; else { fixBeforeRemove(p_tree, p_remove); // 删除节点之前需要重新将树平衡 p_remove->p_parent = p_parent->p_right == p_remove ? p_parent->p_right = NULL : (p_parent->p_left = NULL); // 最后删除节点 } // 释放被删除节点的空间 if (p_remove->p_key) free(p_remove->p_key); if (p_remove) free(p_remove); p_remove = p_remove->p_key = NULL; --p_tree->size; return 1; } void free_RBTree(RBTree *p_tree) { if (!p_tree) return; for (RBNode *p_node = NULL; p_node = p_tree->p_root; ) remove_RBTree(p_node->p_key, p_tree, NULL); free(p_tree); p_tree = NULL; } static int findNode(int(*p_kcmp)(void *, void *, char *), void *p_key, RBNode *p_curr, RBNode **p_res) { if (!p_kcmp || !p_key || !p_res) return 0; RBNode *p_found = NULL; for (char compare = 0; p_curr && !p_found; ) { if (!p_kcmp(p_key, p_curr->p_key, &compare)) return 0; if (compare > 0) p_curr = p_curr->p_right; else if (compare < 0) p_curr = p_curr->p_left; else *p_res = p_found = p_curr; } return 1; } static void rotateLeft(RBTree *p_tree, RBNode *p_rotate) { RBNode *p_right, *p_parent, *p_broLeft; if (!p_tree || !p_rotate || !(p_right = p_rotate->p_right)) // 如果旋转节点的右子节点为空节点,则不需要旋转直接返回 return; // 将旋转节点的右子节点设置为右子节点的左子节点,并将右子节点的左子节点父节点设置为旋转节点 if (p_broLeft = p_rotate->p_right = p_right->p_left) p_broLeft->p_parent = p_rotate; if (!(p_parent = p_right->p_parent = p_rotate->p_parent)) // 右子节点的父节点设置为旋转节点的父节点,如果父节点为空则将右子节点设置为根节点,并将颜色设置为黑色 (p_tree->p_root = p_right)->color = 1; else if (p_parent->p_left == p_rotate) p_parent->p_left = p_right; else p_parent->p_right = p_right; p_right->p_left = p_rotate; p_rotate->p_parent = p_right; } static void rotateRight(RBTree *p_tree, RBNode *p_rotate) { RBNode *p_left, *p_parent, *p_broRight; if (!p_tree || !p_rotate || !(p_left = p_rotate->p_left)) return; if (p_broRight = p_rotate->p_left = p_left->p_right) p_broRight->p_parent = p_rotate; if (!(p_parent = p_left->p_parent = p_rotate->p_parent)) (p_tree->p_root = p_left)->color = 1; else if (p_parent->p_left == p_rotate) p_parent->p_left = p_left; else p_parent->p_right = p_left; p_left->p_right = p_rotate; p_rotate->p_parent = p_left; } static void fixAfterPut(RBTree *p_tree, RBNode *p_current) { for (RBNode *p_parent, *p_gparent, *p_graLeft, *p_graRight; ; ) { if (!(p_parent = p_current->p_parent)) // 当前节点父节点是空节点,适配【场景1】 { p_current->color = 1; break; } if (p_parent->color || !(p_gparent = p_parent->p_parent)) // 当前节点的父节点是黑色节点,或者祖父节点是空节点(父节点是根节点),适配【场景2】 break; if ((p_graLeft = p_gparent->p_left) == p_parent) // 父节点为祖父节点的左子节点 { /* * 节点情况分析: * 1、当前节点不为空,并且为红色节点 * 2、当前节点的父节点不为空,并且为红色节点 * 3、当前节点的祖父节点不为空,并且为黑色节点 */ if ((p_graRight = p_gparent->p_right) && !p_graRight->color) // 当前节点的叔叔节点是红色节点,适配【场景4】 { p_graRight->color = 1; // 将叔叔节点颜色置黑 p_parent->color = 1; // 将父节点颜色置黑 p_gparent->color = 0; // 将祖父节点颜色置红 p_current = p_gparent; // 将祖父节点设为当前节点 } else // 当前节点的叔叔节点是叶子节点或者黑色节点,适配【场景3】 { if (p_current == p_parent->p_right) // 当前节点为父节点的右子节点 { rotateLeft(p_tree, p_current = p_parent); // 将将父节点设为当前节点并将当前节点左旋转 p_gparent = (p_parent = p_current->p_parent)->p_parent; // 重新为父节点和祖父节点赋值 } p_parent->color = 1; // 将父节点颜色置黑 p_gparent->color = 0; // 将祖父节点颜色置红 rotateRight(p_tree, p_gparent); // 将祖父节点进行右旋转 } } else // 父节点为祖父节点的右子节点 { if (p_graLeft && !p_graLeft->color) { p_graLeft->color = 1; p_parent->color = 1; p_gparent->color = 0; p_current = p_gparent; } else { if (p_current == p_parent->p_left) { rotateRight(p_tree, p_current = p_parent); p_gparent = (p_parent = p_current->p_parent)->p_parent; } p_parent->color = 1; p_gparent->color = 0; rotateLeft(p_tree, p_gparent); } } } } static void fixBeforeRemove(RBTree *p_tree, RBNode *p_current) { for (RBNode *p_parent, *p_left, *p_right; p_current // 当前节点不为空 && (p_parent = p_current->p_parent); ) // 当前节点的父节点是空节点,适配【场景1】 { if (!p_current->color) // 当前节点为红色节点,适配【场景2】 { p_current->color = 1; break; } if ((p_left = p_parent->p_left) == p_current) // 如果当前节点为父节点的左子节点 { /* * 节点情况分析: * 1、当前节点是黑色节点 * 2、当前节点的兄弟节点不是叶子结点 */ if (!(p_right = p_parent->p_right)->color) // 当前节点的兄弟节点为红色节点,适配【场景4】 { /* * 节点情况分析: * 1、父节点为黑色节点; * 2、兄弟节点的左右子节点为黑色节点; */ p_right->color = 1; // 将兄弟节点颜色置黑 p_parent->color = 0; // 将父节点颜色置红 rotateLeft(p_tree, p_parent); // 将父节点左旋转(当前节点仍然是父节点的左子节点) p_right = p_parent->p_right; // 重新获取当前节点的兄弟节点 } /* * 节点情况分析: * 1、当前节点的兄弟节点一定为黑色节点 */ RBNode *p_broLeft = p_right->p_left, *p_broRight = p_right->p_right; if ((!p_broRight || p_broRight->color) && (!p_broLeft || p_broLeft->color)) { // 当前节点兄弟节点的左右子节点不存在红色节点,适配【场景5】 /* * 节点情况分析: * 情况1:当前节点兄弟节点的左右子节点都为黑色节点 * 情况2:当前节点兄弟节点的左右子节点都为叶子节点 */ p_right->color = 0; // 将兄弟节点颜色置红 p_current = p_parent; // 将父节点设为当前节点 } else // 当前节点的兄弟节点至少有一个红色子节点,适配【场景3】 { if (!p_broRight || p_broRight->color) { // 兄弟节点的右子节点为叶子节点或者黑色节点,则兄弟节点的左子节点一定为红色节点 p_broLeft->color = 1; // 将兄弟节点的左子节点颜色置黑 p_right->color = 0; // 将兄弟节点颜色置红 rotateRight(p_tree, p_right); // 将兄弟节点右旋转 p_right = p_parent->p_right; // 重新获取右子节点 p_broRight = p_right->p_right; } p_right->color = p_parent->color; // 将兄弟节点的颜色置为父节点的颜色 p_broRight->color = 1; // 将兄弟节点的右子节点颜色置黑 p_parent->color = 1; // 将父节点颜色置黑 rotateLeft(p_tree, p_parent); // 将父节点左旋转 break; } } else // 当前节点为右子节点 { if (!p_left->color) { p_left->color = 1; p_parent->color = 0; rotateRight(p_tree, p_parent); p_left = p_parent->p_left; } RBNode *p_broLeft = p_left->p_left, *p_broRight = p_left->p_right; if ((!p_broLeft || p_broLeft->color) && (!p_broRight || p_broRight->color)) { p_left->color = 0; p_current = p_parent; } else { if (!p_broLeft || p_broLeft->color) { p_broRight->color = 1; p_left->color = 0; rotateLeft(p_tree, p_left); p_left = p_parent->p_left; p_broLeft = p_left->p_left; } p_left->color = p_parent->color; p_broLeft->color = 1; p_parent->color = 1; rotateRight(p_tree, p_parent); break; } } } }
- C代码测试用例:
#include <stdlib.h> #include <stdio.h> #include <string.h> #include <time.h> #include "RBTree.h" #define _VALUE_SIZE 20 static int kcmp(void *p_key1, void *p_key2, char *p_res) { int compare = *((int *)p_key1) - *((int *)p_key2); if (compare > 0) *p_res = 1; else if (compare < 0) *p_res = -1; else *p_res = 0; return 1; } RBTree *init_RBTree(int n_size, int max_key) { RBTree *p_tree = NULL; p_tree = create_RBTree(kcmp); if (!(p_tree = create_RBTree(kcmp))) { printf("创建红黑树出现错误\n"); return NULL; } int *p_key = NULL; char *p_value = NULL; srand((unsigned int)time(NULL)); for (int i = 0; i < n_size; ++i) { if (!(p_key = (int *)malloc(sizeof(int)))) { printf("开辟key空间失败\n"); return p_tree; } if (!(p_value = (char *)malloc(_VALUE_SIZE))) { if (!p_key) free(p_key); p_key = NULL; printf("开辟value空间失败\n"); return p_tree; } _itoa_s((*p_key = rand() % max_key), p_value, _VALUE_SIZE, 16); if (!put_RBTree(p_key, p_value, p_tree)) { printf("向红黑树中插入节点失败\n"); return p_tree; } } return p_tree; } void testFind_RBTree() { RBTree *p_tree = NULL; if (!(p_tree = init_RBTree(100, 1000))) { printf("红黑树初始化失败\n"); return; } RBNode *p_root = p_tree->p_root; printf("初始化红黑树成功: root_key=%d, size=%d\n", *((int *)p_root->p_key), p_tree->size); srand((unsigned int)time(NULL)); int key = rand() % 1000; void *p_value = NULL; find_RBTree(&key, p_tree, &p_value); if (p_value) printf("key=%d, value=%s\n", key, (char *)p_value); else printf("key=%d, value=NULL\n", key); free_RBTree(p_tree); // 释放红黑树 } void testPutAndRemove_RBTree() { RBTree *p_tree = NULL; if (!(p_tree = init_RBTree(100, 1000))) { printf("红黑树初始化失败\n"); return; } RBNode *p_root = p_tree->p_root; printf("初始化红黑树成功: root_key=%d, size=%d\n", *((int *)p_root->p_key), p_tree->size); char isRBTree = 0; for (int i = 0; i < 20; ++i) { RBNode *p_node = p_tree->p_root; if (p_node) { printf("删除[root_key=%d]后,", *((int *)p_node->p_key)); remove_RBTree(p_node->p_key, p_tree, NULL); is_RBTree(p_tree, NULL, &isRBTree); printf("p_tree[%s]一颗红黑树, size=%d\n", isRBTree ? "还是" : "不是", p_tree->size); } } free_RBTree(p_tree); // 释放红黑树 } int main(void) { testPutAndRemove_RBTree(); //testFind_RBTree(); system("pause"); return EXIT_SUCCESS; }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号