Google 矩阵和Page Rank的简单介绍
Page Rank是Google排名算法法则的一部分，是Google用于标识网页的等级/重要性的一种方法，是Google用来衡量一个网站好坏的标准。在揉合了诸如Title标识和Keywords标识等所有其它因素之后，Google通过PageRank来调整结果，使那些更具“等级/重要性”的网页在搜索结果中的排名获得提升，从而提高搜索结果的相关性和质量。其级别从0到10级，10级为满分。PR值越高说明该网页越重要。
Google的PageRank根据网站的外部链接和内部链接的数量和质量来衡量网站的价值。
[以上引自：百度百科，详细见http://baike.baidu.com/view/1518.htm，就不多作介绍了]
Google矩阵及PageRank的求解方法
1. Google矩阵
Google矩阵，是表现网页间链接关系的，如果有N个页面，就可以写出N×N的矩阵，其中的元素pij，如果存在从页i被页j指向的链接，那么pij就大于0，反之就等于0，同时各列矢量总和为1，现在以一题目为例，说明如何计算Google矩阵及PageRank。
假设有A,B,C,D,E五个网页，其中
1)A网页有链接指向B,C,D
2)B网页有链接指向A,E
3)C网页有链接指向A,E
4)D网页有链接指向C
5)E网页有链接指向A,C
请写出这个网页链接结构的Google矩阵
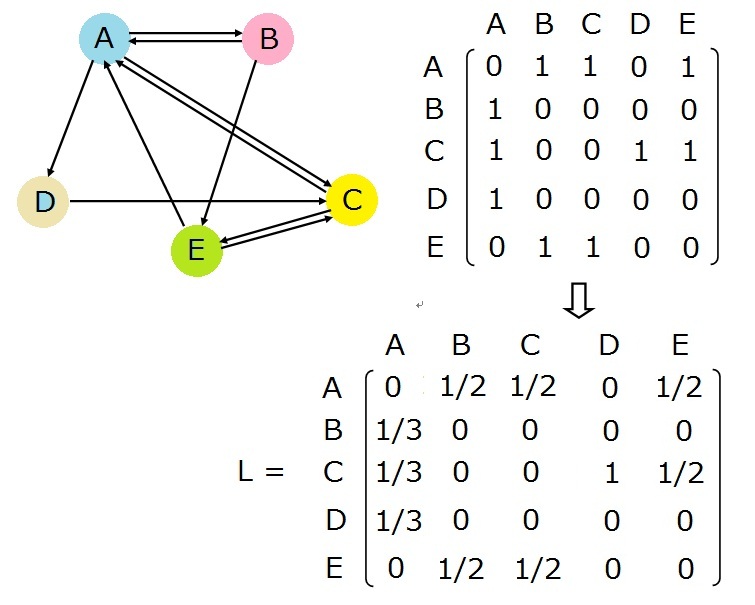
这样，我们就得到了Google的初始矩阵L（也有资料叫这转移矩阵）。
2. PageRank的求解
得到初始矩阵后，我们就可以得到PR值，当只有a概率的用户会点击网页链接，剩下(1-a)概率的用户会跳到无关的页面上去，而访问的页面恰好是这5个页面中A的概率只有(1-a)/5（a是阻尼系数，Google取a等于0.85），所以真正的Google矩阵
于是得到q（n)=G*q(n-1),特征向量q的初始值为值为1的5*1矩阵，直到q（n)=q(n-1)，q(n)就是PR的值。
编程实现了此PageRank的计算（Java）
package com.hadoop;
public class PageRank {
/**
* 矩阵g乘以矩阵p
* @param g
* @param p
* @return 矩阵g乘以矩阵p的结果矩阵
*/
private static float[] multiMatrix(float[][] g, float[] p){
float[] multiResult = new float[p.length];
for(int i=0; i<g.length; i++){
float rowResult = 0.0f;
for(int j=0; j<g.length; j++){
rowResult+=g[j]*p[j];
}
multiResult = rowResult;
}
return multiResult;
}
/**
* 根据初始矩阵计算真正的Google矩阵
* @param 初始矩阵
* @param weight
* @param oneMatrix
* @return 真正的Google矩阵
*/
private static void getGoogleMatrix(float[][] transitionMatrix, float weight){
//transitionMatrix*weight
for(int i=0; i<transitionMatrix.length; i++){
for(int j=0; j<transitionMatrix.length; j++){
transitionMatrix[j] *= weight;
transitionMatrix[j] += (1-weight)/transitionMatrix.length;
}
}
}
/**
* 如果pageRankN=pageRankN_1,返回true；否则，返回false
* @param pageRankN
* @param pageRankN_1
* @return
*/
private static boolean compareMatrix(float[] pageRankN, float[] pageRankN_1){
for(int i=0; i<pageRankN.length; i++){
if(pageRankN-pageRankN_1>0.0000001){
return false;
}
}
return true;
}
/**
*
* @param args
*/
public static void main(String[] args) {
// TODO Auto-generated method stub
float[][] transitionMatrix={{0,1/2f,1/2f,0,1/2f},{1/3f,0,0,0,0},{1/3f,0,0,1,1/2f},{1/3f,0,0,0,0},{0,1/2f,1/2f,0,0}};//初始矩阵
float[] p={1,1,1,1,1};
float weight = 0.85f; //a的值
//真正的Google矩阵
getGoogleMatrix(transitionMatrix, weight);
//q（n)=G*q(n-1),如果q(n)=q(n-1),q(n)是PageRank
float[] pageRank = multiMatrix(transitionMatrix, p);
while(!compareMatrix(pageRank, p)){
p = pageRank;
pageRank = multiMatrix(transitionMatrix, p);
}
//输出PageRank
for(int i=0; i<pageRank.length; i++){
System.out.println(pageRank);
}
}
}
输出结果：
1.4308448
0.5554062
1.4542446
0.5554062
1.0041016
