coloring 图着色

coloring 图着色

图着色也称为“ $ m $着色问题” , 由最多 $ m $ 种颜色的给定图着色组成 ,
使相邻的顶点不被赋予相同的颜色

图着色问题（Graph Coloring Problem, GCP） 又称着色问题，是最著名的NP-完全问题之一。道路着色问题（Road Coloring Problem）是图论中最著名的猜想之一。

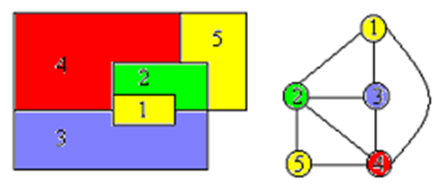
数学定义：给定一个无向图 $ G=（V, E）$，其中 $ V $ 为顶点集合，$ E $ 为边集合，图着色问题即为将 $ V $ 分为$ K $个颜色组，每个组形成一个独立集，即其中没有相邻的顶点。其优化版本是希望获得最小的 $ K $值。

简介

图的 $ m $ -着色判定问题——给定无向连通图 $ G $ 和 $ m $ 种不同的颜色。用这些颜色为图G的各顶点着色，每个顶点着一种颜色，是否有一种着色法使G中任意相邻的2个顶点着不同颜色?

图的 $ m $-着色优化问题——若一个图最少需要 $ m $ 种颜色才能使图中任意相邻的2个顶点着不同颜色，则称这个数 $ m $ 为该图的色数。求一个图的最小色数 $ m $ 的问题称为 $ m $-着色优化问题。

路线着色问题

$ G $ 是一个有限有向图并且 $ G $的每个顶点的出度都是 $ k \(。\) G $ 的一个同步着色满足以下两个条件：

• 1)$ G $ 的每个顶点有且只有一条出边被染成了 $ 1 $ 到 $ k $ 之间的某种颜色；
• 2)$ G $ 的每个顶点都对应一种走法，不管你从哪里出发，按该走法走，最后都结束在该顶点。
  

有向图 $ G $ 存在同步着色的必要条件是 $ G $ 是强连通而且是非周期的。一个有向图是非周期的是指该图中包含的所有环的长度没有大于 $ 1 $ 的公约数。路线着色定理这两个条件(强连通和是非周期)也是充分的。也就是说,有向图 $ G $ 存在同步着色当且仅当G是强连通而且是非周期的。

道路着色问题（Road Coloring Problem）是图论中最著名的猜想之一。通俗的说，这个猜想认为，可以绘制一张“万能地图”，指导人们到达某一目的地，不管他们原来在什么位置。这个猜想最近被以色列数学家艾夫拉汉· 特雷特曼(Avraham Trahtman)在2007年9月证明。

特雷特曼在数学上的这一成果极为令人瞩目，英国《独立报》为此事专门发表了一篇题为“身无分文的移民成了数学超级明星”的文章，给予了高度的评价。

以色列人也为特雷特曼取得的成就感到无比的骄傲。特拉维夫电视台中断了正常的节目播放，以第一时间发布了这一重大消息，连中东其他国家的主流媒体也作了大篇幅的相关报道。

得知特雷特曼解决这一难题的消息后，多年从事路线着色问题研究的加拿大数学家乔尔·弗里德曼说，“路线着色问题的解决令数学共同体非常兴奋。”读过特雷特曼论文的中国数学家和语言学家周海中教授认为，特雷特曼的数学知识非常渊博，解题方法十分巧妙，这一谜题得到破解，无疑是数学史上的一个华彩乐章。

算法

点着色问题有简单的时间复杂度为 $ O(3^n) $ 的算法，即设 $ f(S) $ 表示集合的色数，则。

算法描述

$ color[n] $ 存储 $ n $ 个顶点的着色方案，可以选择的颜色为 $ 1 $ 到 $ m $。

当 $ t=1 $ 时，对当前第 $ t $ 个顶点开始着色：若$ t>n \(，则已求得一个解，输出着色方案即可。否则，依次对顶点\) t $ 着色 $ 1-m $， 若 $ t $ 与所有其它相邻顶点无颜色冲突，则继续为下一顶点着色；否则，回溯，测试下一颜色。

范例：

第一行，一个整数 $ n(1 < n < 100) $ ，表示参加考试的人数。 　

第二行，一个整数 $ m $，表示接下来有 $ m $ 行数据

以下 $ m $ 行每行的格式为：两个整数 $a，b $，用空格分开 $ (1<=a,b<=n) $ 表示第 $ a $ 个人与第 $ b $ 个人认识。

输出格式一行一个整数，表示最少分几个考场

代码

[coloring.py]{..\src\backtracking\coloring.py}

"""
Prepare
   1. sys.path 中增加 TheAlgorithms\src 子模块

"""
import sys
sys.path.append('E:\dev\AI\TheAlgorithms\src')

案例一：

    >>> neighbours = [0,1,0,1,0]
    >>> colored_vertices = [0, 2, 1, 2, 0]

    >>> color = 1
    >>> valid_coloring(neighbours, colored_vertices, color)
    True

    >>> color = 2
    >>> valid_coloring(neighbours, colored_vertices, color)
    False

from backtracking.coloring import valid_coloring
"""
"""
neighbours = [0,1,0,1,0]
colored_vertices = [0, 2, 1, 2, 0]

color = 1
valid_coloring(neighbours, colored_vertices, color)

True

案例二：

>>> graph = [[0, 1, 0, 0, 0],
...          [1, 0, 1, 0, 1],
...          [0, 1, 0, 1, 0],
...          [0, 1, 1, 0, 0],
...          [0, 1, 0, 0, 0]]

>>> max_colors = 3
>>> color(graph, max_colors)
[0, 1, 0, 2, 0]

```python
from backtracking.coloring import color
"""
"""
graph = [[0, 1, 0, 0, 0],
         [1, 0, 1, 0, 1],
         [0, 1, 0, 1, 0],
         [0, 1, 1, 0, 0],
        [0, 1, 0, 0, 0]]
max_colors = 3
color(graph, max_colors)

[0, 1, 0, 2, 0]