Redis设计与实现—跳跃表、压缩列表
前言
Redis设计与实现读书笔记,基础数据结构部分——跳跃表与压缩列表
@
一、跳跃表
1.1 跳跃表概念
跳表(SkipList) 是用于有序元素序列快速搜索查找的一个数据结构,跳表是一个随机化的数据结构,实质上是一种可进行二分查找的有序链表。跳表在原有的有序链表上面增加了多级索引,通过索引来实现快速查找。同时跳表不仅能够提高搜索性能,还能够提高插入删除操作的性能。总的来说性能和红黑树、AVL树不相上下,但是跳表原理更加简单,实现起来更加简单。
Redis 使用跳跃表作为有序集合(Zset)的底层实现之一,如果一个有序集合包含的元素数量比较多,又或者有序集合中元素的成员是比较长的字符串时,Redis 就会使用跳跃表来作为有序集合键的底层实现。
1.2 Redis中跳跃表的实现
Redis中的跳跃表由 zskiplistNode(表示跳跃表节点)、zskiplist(跳跃表,保存跳跃表节点的相关信息,比如节点数量、指向表头节点和表尾节点的指针)。
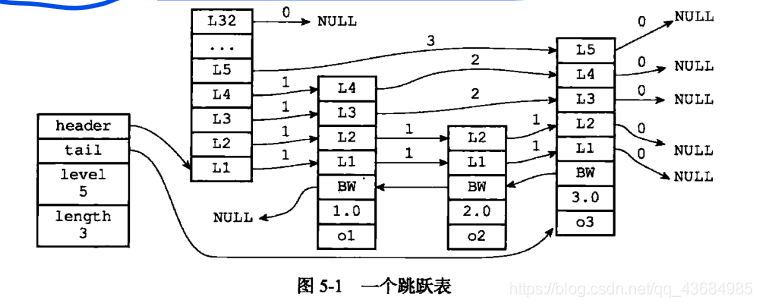
typedef struct zskiplist {
// 表头节点和表尾节点
struct zskiplistNode *header,*tail;
// 表中节点的数量
unsigned long length;
// 表中层数最大的节点的层数
int level;
} zskiplist;
1.3 跳跃表节点(zskipListNode)
typedef struct zskiplistNode {
// 层
struct zskiplistLevel {
// 前进指针
struct zskiplistNode *forward;
// 跨度
unsigned int span;
} level[];
// 后退指针
struct zskiplistNode *backward;
// 分值
double score;
// 成员对象
robj *obj;
} zskiplistNode;
- 层
每次创建一个新跳跃节点时,程序都根据幂次定律生成一个介于1到32之间的值作为 level 数组的大小。跳跃节点中的level 数组包含多个元素,其中每个元素包含一个指向其他节点的指针,程序可以通过这些层来加快访问其他节点的速度,一般来说,层的数量越多,访问其他节点的速度就越快。 - 前进指针
跳表节点中每层都有一个前进指针,通过前进指针访问到下一个节点; - 跨度
跨度用来计算排位(rank)的,在查找某个节点的过程中,将沿途访问过的所有层的跨度累计起来,得到的结果就是目标节点在跳跃表中的排位。跨度用于记录两个节点之间的距离,跨度越大相距的越远。 - 后退指针
用于从表尾向表头访问,与可以一次跳过多个前进指针不同,因为每个节点只有一个后退指针,因此一次只能后退一步。
1.4 手动模拟跳跃表
1.4.1 数据结构
/**
* 跳跃节点
* @param <T>
*/
public class SkipNode<T> {
public int key;
public T value;
public SkipNode right,down;
public SkipNode(int key, T value) {
this.key = key;
this.value = value;
}
public SkipNode(){
this.key = Integer.MIN_VALUE;
value = null;
}
}
/**
* 跳跃表
*/
public class SkipList<T> {
//头节点
public SkipNode<T> headNode;
//当前跳表层数(最高)
public int highlevel;
//默认最大层数
public final int MAX_LEVEL=32;
//添加节点时是否继续添加,计算概率
public Random random;
public SkipList() {
random = new Random();
headNode = new SkipNode(Integer.MIN_VALUE,null);
highlevel = 0;
}
}
1.4.2 查找
二分查找的思想,不过每一轮的二分查找为遍历当前链表的一层
/**
* 查找节点
* @param key
* @return
*/
public SkipNode search(int key){
SkipNode temp = headNode;
while (temp!=null) {
if(temp.key==key)
{
return temp;
}
else if(temp.right.key<key)
{
temp=temp.right;
}
else
{
temp=temp.down;
}
}
return null;
}
1.4.3 删除
找到每层待删除节点的前一个节点,然后进行删除
/**
* 删除节点
* @param key
*/
public void delete(int key){
SkipNode temp = headNode;
while (temp!=null) {
if(temp.right==null)
{
temp=temp.down;
}
else if(temp.right.key==key)
{
temp.right=temp.right.right;
temp=temp.down;
}
else if(temp.right.key<key)
{
temp=temp.right;
}
else
{
temp=temp.down;
}
}
}
1.4.4 插入
插入就比较复杂了,因为需要考虑插入多少层,每层在哪里插入。
我们通过随机化的方法来判断是否继续向上层插入索引,产生一个[0-1]的随机数,如果小于0.5就向上插入索引,插入完毕后再次使用随机数判断是否向上插入索引。
另外一个问题,从下往上插入时怎么找到上层待插入的节点位置? 最简单的方式,从初始节点开始往下查找,用栈来记录应该插入位置的前一个节点,直到最后一层。然后逐层退栈,在每层进行节点插入。
/**
* 增加节点
* @param node
*/
public void add(SkipNode node){
// 查询节点是否已经存在
int key = node.key;
SkipNode resNode = search(key);
if(resNode!=null){
resNode.value=node.value;
return;
}
// 收集path并压栈
Stack<SkipNode> stack = new Stack<SkipNode>();
SkipNode head = headNode;
while (head!=null) {
if(head.right==null)
{
stack.add(head);
head=head.down;
}
else if(head.key>node.key)
{
stack.add(head);
head=head.down;
}
else{
head=head.right;
}
}
// 弹栈并且从下往上插入节点
int tmpLevel = 1;
SkipNode downNode = null;
while (!stack.empty()) {
// 插入到当前层
SkipNode preNode = stack.pop();
SkipNode newNode = new SkipNode(node.key,node.value);
newNode.down = downNode;
downNode = newNode;
if(preNode.right==null){
preNode.right=newNode;
}
else {
newNode.right=preNode.right;
preNode.right=newNode;
}
// 考虑是否向上插入, 1/2的概率插入
if(tmpLevel>MAX_LEVEL)
break;
double num = random.nextDouble();
if(num > 0.5)
break;
tmpLevel++;
/**
* 插入到了最高层,刚好随机数小于0.5,还要继续网上面插入一个节点
* 解决:网上再建一层,然后新建一个节点作为head,将head加入到stack中
*/
if(tmpLevel>highlevel){
highlevel = tmpLevel;
SkipNode highNode = new SkipNode();
highNode.down = headNode;
headNode = highNode;
stack.add(headNode); //压栈
}
}
}
二、整数集合
2.1 介绍
整数集合(intset) 是作为集合键的底层实现之一,当一个集合只包含整数值元素,并且这个集合的元素数量不多时,Redis就会使用整数集合作为集合键的底层实现。整数集合中保证不会出现重复元素,满足set 结构的要求。
比如命令 sadd numbers 1 3 5 7 9 这样创建的 set集合的底层使用的就是整数集合。
2.2 整数集合的实现
typedef struct inset {
// 编码方式
uint32_t encoding;
// 集合包含的元素数量
uint32_t length;
// 保存元素的数组
int8_t contents[];
} intset;
其中 contents 是整数集合的底层实现,整数集合的每个元素都是 contents数组的一个数组项(item)。
2.3 整数集合升级
每当我们要将一个新元素添加到整数集合里面时,并且新元素的类型比整数集合现在所有元素的类型都要长时,就会触发整数集合的升级,升级指集合内的元素类型转换为新元素相同的类型,最后才添加进整数集合里面。
升级步骤:
1)根据新元素的类型,扩展整数集合底层数组的空间大小,并为新元素分配空间;
2)将底层数组现有的所有元素都转换为新元素的类型;
3)将新元素添加到底层数组里面。
三、压缩列表
3.1 介绍
前一章介绍过,Redis中的列表底层实现之一是双向链表,不过前提是列表内存储的元素很多或者是长度比较长的字符串;而当列表中存储的是长度比较短的字符串或者比较小的整数值时,采用的是压缩列表的模式。比如命令 rpush lst 1 3 5 10086 "heelo" "sdfsd"。压缩列表(ziplist) 是列表键和哈希键的底层实现之一。
3.2 压缩列表的构成
压缩列表是为了节约Redis的内存而开发的,是由一系列的特殊编码的连续内存块组成的顺序型数据结构。一个压缩列表可以包含任意多个节点(entry),每个节点可以保存一个字节数组或者一个整数值。

zlbytes:记录整个压缩列表占用的内存字节数;zltail:记录压缩列表表尾节点距离压缩列表的起始地址有多少字节,可以计算出表尾节点的地址;zllen:压缩列表包含的节点数量;entryX:列表节点;zlend:标记压缩列表的末端。
3.3 压缩列表节点的组成

-
previous_entry_length:前一个节点的长度,值可以是1字节或者5字节。
如果前一个节点的长度小于 254字节,那么previous_entry_length属性的长度为1字节;如果大于等于254字节,那么长度为5字节。
由于每个节点保存了前一个节点的长度,那么程序可以通过指针运算,根据当前的起始地址来计算出前一个节点的起始地址。压缩列表从表尾向表头遍历操作就是使用这一原理来实现的,只要我们拥有了一个指向某个节点的起始地址,就能通过previous_entry_length属性来不断获取到前一个节点,最终到达表头节点。 -
encoding:记录节点的content属性所保存的数据的类型以及长度; -
content:负责保存节点的值,节点值可以是一个字节数组或者整数,值的类型和长度由节点的encoding属性决定。
3.4 连锁更新的问题
每个节点的 previous_entry_length 属性记录了前一个节点的长度,而且该属性值所占用的字节大小与前一个节点的长度有关,因此如果连续多个节点的长度都处于一个边界范围,一旦其中某个节点的被更新并且需要调整后面一个节点的previous_entry_length 时,就会触发连锁更新的问题。 详细可以查看 《Redis设计与实现》P57、P58


连锁更新在最坏情况下需要对压缩列表执行N次空间重分配操作,而每次空间分配的最坏复杂度为O(N),所以连锁更新的最坏复杂度为O(N^2)。
连锁更新需要在压缩列表中恰好有多个连续的、长度介于250字节至253字节之间的节点,连锁更新才有可能被触发,但是实际上这种情况发生的概率很小。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号