傅里叶变换

周期函数的傅里叶变换

傅里叶变换最开始需要从傅里叶级数开始讲起

• 傅里叶级数

  一个周期信号\(f(t)\), 周期为\(T\)， 角频率为 \(w_0 = 2\pi f_0 = \frac{2\pi}{T}\)，可以展开成如下形式:

  \[\begin{align*} 三角函数基的傅里叶展开： f(t) &= a_0 + a_1\cos w_0 t + a_2\cos 2w_0 t + a_3\cos 3w_0 t + ... \\ & \hspace{1.2cm} + b_1\sin w_0 t + b_2\sin 2w_0 t + b_3\sin 3w_0 t + ... \\ &= a_0 + \sum_{n=1}^{\infty}(a_n\cos nw_0t+b_n\sin nw_0t) \end{align*} \]

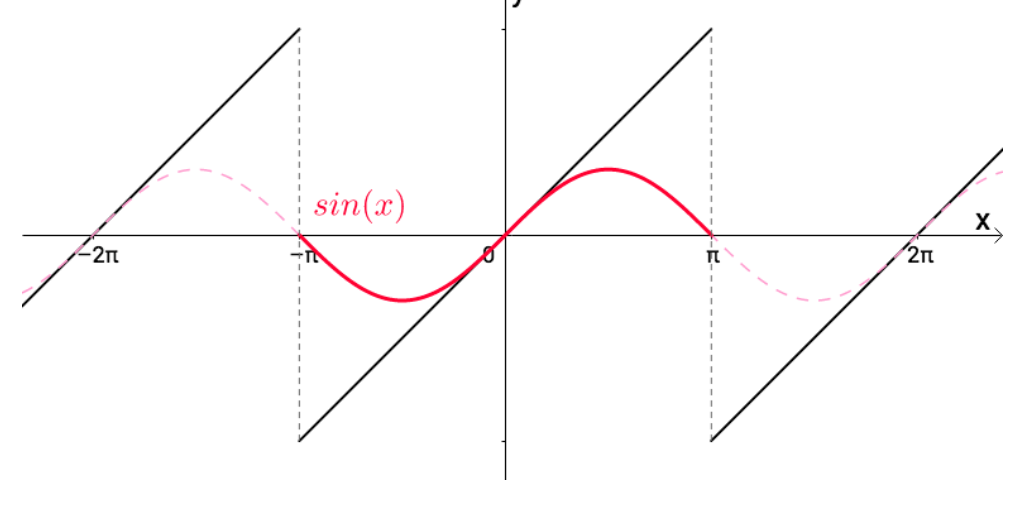
从含义上理解，我们知道是用无限个缩放周期去拟合这个模拟函数，如下图：

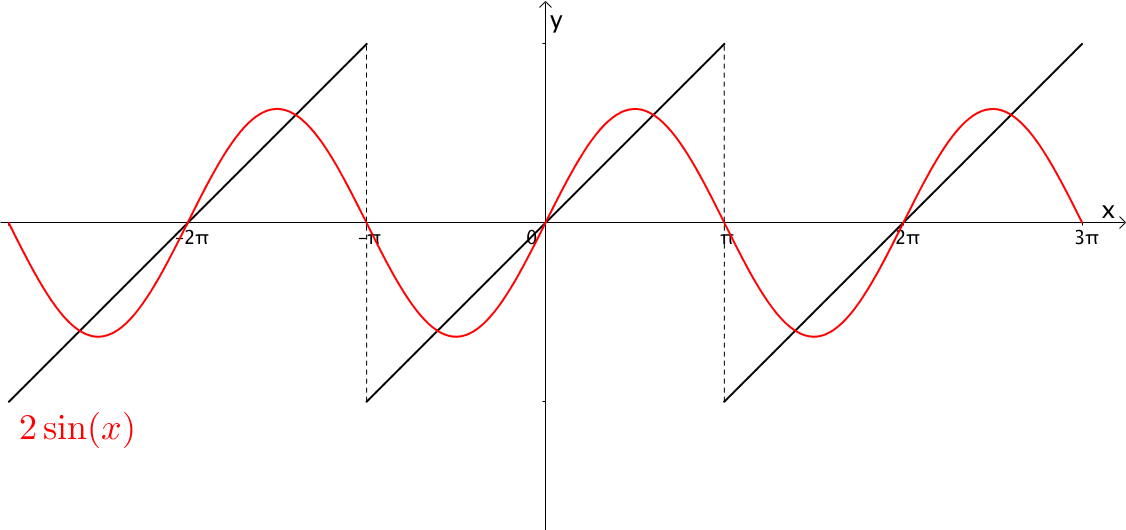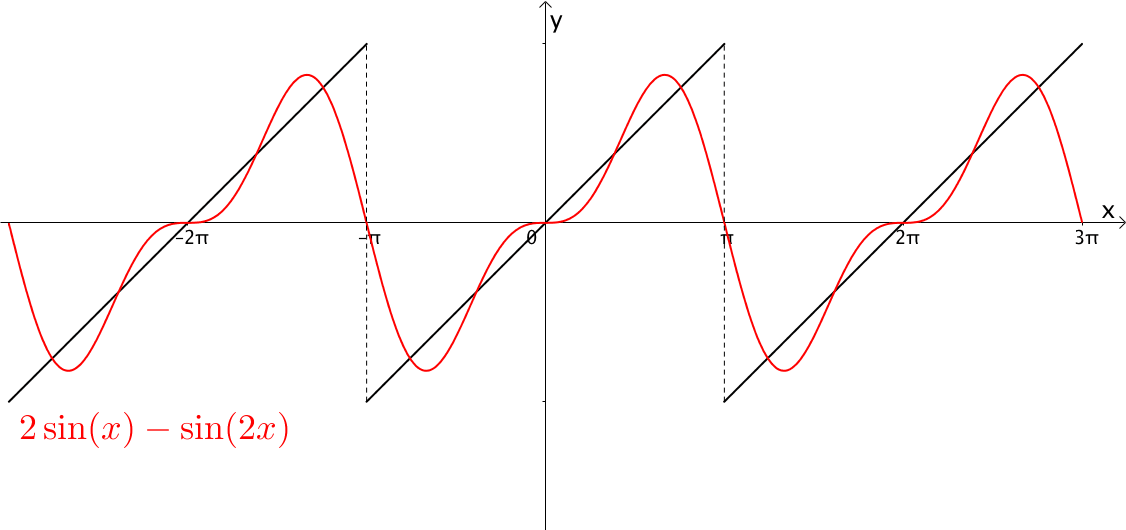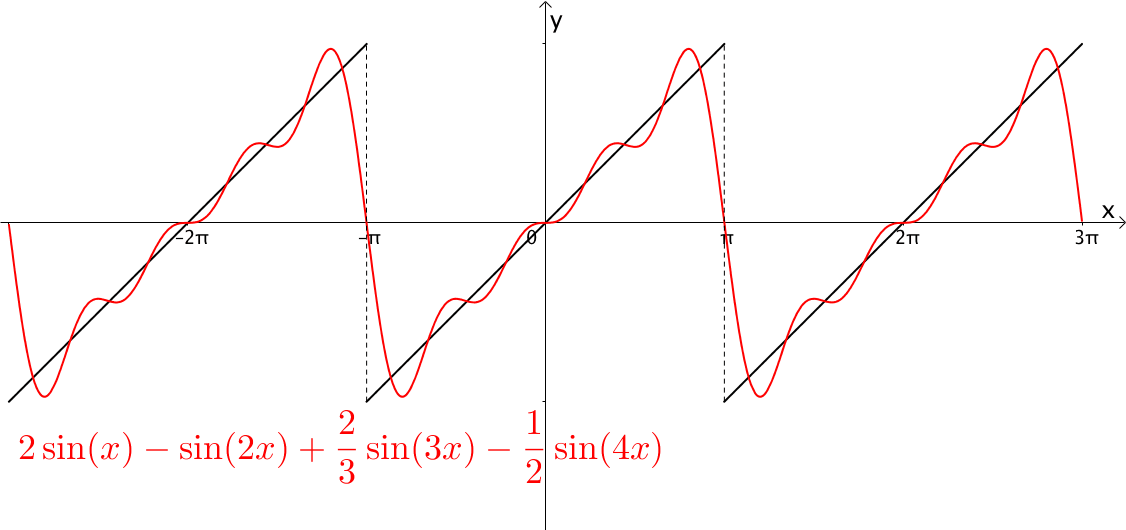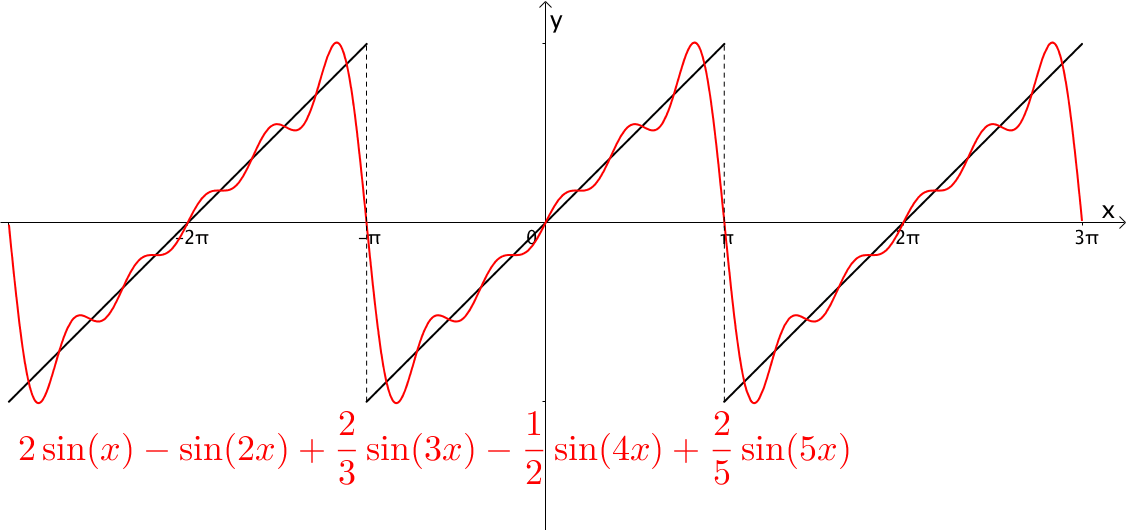
但从数学上解释，仔细观察，就知道就可以体会到\(f(t)\)在\(cosnw_0 t\)以及\(\sin nw_0t\)做分解，之所以能这么分解是因为正余弦组成了一组正交基

介绍正交基之前要先知道函数的正交性： 高中知识告诉我们 一个二维空间的向量是由x, y轴的单位向量\(\vec{x}=(1,0), \vec{y}=(0,1)\)构成，这俩个向量具有正交性，因为它们的内积(投影)为:\(\vec{x} · \vec{y}= 1 * 0 + 0 * 1 = 0\), 同样把正交扩展至函数，当函数的内积如果为0那么两个函数正交，比如说两个函数 \(f(x) 和 g(x)\), 那么$ \int_{-\infty}^{+\infty}f(x)g(x)dx = 0$, 则它们正交，向量空间的内积是对应每一维相乘然后算总和，而函数可以微分化后看成无线维，所以函数的内积运算是积分

\(cosnw_0 t\)以及\(\sin nw_0t\)实际上构成的正交函数，它们之中任意两个内积为0（很好证明），所以可以用他们来做基分量然后组合成\(f(t)\)

\[ \{1, \cos w_0x, \sin w_0x, \cos 2w_0x, \sin 2w_0x, \cos 3w_0x, \sin 3w_0x, \cos 4w_0x, \sin 4w_0x ...\} \\ \]

由于这组正交函数所对应的定义域\(x \in[-\infty, +\infty]\), 值域\(f(x) \in[-\infty, +\infty]\), 所以可以进行线性组合为\(f(t)\)，同时这组三角函数的角频率必为\(w_0\)倍数，很好理解，是因为需要同倍数周期的函数进行叠加， 而\(a_n, b_n\)可以理解成这些维度的系数，或者说\(f(t)\)在这些维度上的投影，要想确定这些值实际上是一个投影的过程，将会在下面得到

• 复指数形式的傅里叶级数

为什么要引入这个复指数基，逻辑是这样子的，对于一个普通周期函数

\[f(x) = k\cos(x + θ) \]

如果单纯用余弦/正弦函数去表示的话，θ无法表示出来的, 因为相位θ的存在，正确的构造思路应该是从这个高中公式开始去入手构造，那么就有正余弦了：

\[acosx + bsinx = \sqrt{a^2 +b^2}sin(x + θ)\\ θ=arctan\frac{b}{a} \]

所以需要搞一个sin和cos同时构成的基序列，使得相位θ存在，这是三角基傅里叶级数为什么既有正弦也有余弦的原因(虽然正弦和余弦是可以转换的)

而复指数傅里叶级数，则是说既然你同时要有\(a\cos{x} + b\sin{x}\)，但是两个东西我看着碍眼，我可以利用欧拉公式\(e^{ix} = \cos x + j\sin x\)一个去表示你这两个东西，只要把\(e^{ix}\)系数构造好，那就可以\(jsinx\)转成\(bsinx\)，这就是它的思想。

所以我们更习惯使用下面这么一组复指数正交基去表示，其中\(j\)是虚数单位也就是我们常见的\(i\)

\[ \{e^{-jnw_0x}, ..., e^{-j3w_0x}, e^{-2jw_0x}, e^{-jw_0x}, e^{j0w_0x}, e^{jw_0x}, e^{j2w_0x}, e^{j3w_0x},...,e^{j4w_0x}\} \]

这组正交基的定义域\(x \in[-\infty, +\infty]\), 值域\(f(x)\) 除了是\([-\infty, +\infty]\), 同时还在一个复数空间上，所以用来表示一个实数空间的东西没有问题(三维变量表示二维变量，只需要把多出的维度消除掉即可)， 在这组正交基下，\(f(t)\)可以在区间\([-\frac{T}{2}, \frac{T}{2}]\)展开成如下形式:

\[复指数基的傅里叶展开: f(t) = \sum_{k = -\infty}^{+\infty}c_ke^{jkw_0t} \]

• 投影的计算

我们知道\(c_k\)相当于f(t)在各个分量上的系数，或者说f(t)在\(e^{jnw_0t}\)上的投影，投影的计算方式在二维向量中内积已经做过计算:

\[\vec{x} · \vec{y}= |\vec{x}||\vec{y}|·\cos {\theta} \\ \vec{x} 在 \vec{y}上的投影为:|\vec{x}| cos {\theta} = \frac{\vec{x}·\vec{y} }{ \vec{y}} \]

所以在函数上也是一样的定义，内积的值/基分量，对于\(C_k\)的值如下:

\[\begin{align*} c_k &= \frac{<f(t), e^{jkw_0t}>}{<e^{jkw_0t}, e^{jkw_0t}>} \\ &= \frac{\int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)e^{-jkw_0t}dt}{\int_{-\frac{T}{2}}^{\frac{T}{2}}e^{jkw_0t}e^{-jkw_0t}dt}\\ &= \frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)e^{-jnw_0t}dt \end{align*} \]

其中有两个细节，一是复数的乘法是乘以第二个乘数的共轭的，所以看到\(e^{jkw_0t}\)变成了\(e^{-jkw_0t}\), 第二是关于被除数\({<e^{jkw_0t}, e^{jkw_0t}>}\)的理解上，因为我们这里算的是以\(e^{jkw_0t}\)为基的系数，所以除的是\(e^{jkw_0t}\)的内基，而不是一个\(e^{jkw_0t}\)

• 总结

  到这里其实就很明确了，一个周期为T的函数，可以由周期为nT(n= ..., -3, -2, -1, 0 1, 2, 3, ...)的正余弦周期函数组合构成，为了表示方便所以用复指数\(e^{jkw_0t}\)方式去代替这些正余弦，而要求这些分量的系数，实际上就是求f(t)在这些基上投影，计算方式是\(\frac{f(t)与积分量的内积}{基分量与基分量的内积}\)， 所以往往能看到这东西\(f(t)e^{-jnw_0t}\)， 它实际上就是:f(t)与积分量的内积

非周期函数的傅里叶变换

在上一节已经知道了，对于周期函数\(f(t)\)在区间\([-\frac{T}{2}, \frac{T}{2}]\) 做傅里叶展开得

\[\hspace{4cm} f(t) = \sum_{k = -\infty}^{+\infty}c_ke^{ikw_0t} \hspace{4cm}(2.1)\\ c_n = \frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)e^{-jkw_0t}dt \]

对于非周期函数，可以认为\(T→\infty\)，此时\(w_0 = \frac{2\pi}{T} →\) 0, 所以微分化后，可以认为是\(w=kw_0, w_0 = \Delta w\), 此时

\[c_n = \frac{\Delta w}{2\pi} \int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)e^{-jwt}dt \]

将\(c_n\)代入2.1得

\[f(t) = \frac{1}{2\pi} \sum_{k = -\infty}^{+\infty} (\int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)e^{-jwt}dt) e^{jkw_0t}\Delta w \]

由于\(\Delta w,T→\infty\)，

\[f(t) = \frac{1}{2\pi} \int_{-\infty}^{+\infty} (\int_{-\infty}^{+\infty}f(t)e^{-jwt}dt) e^{jkwt}dw \\ 记： F(w) = \int_{-\infty}^{+\infty}f(t)e^{-jwt}dt \hspace{2cm}(傅里叶变换)\\ 则: f(t) = \frac{1}{2\pi} \int_{-\infty}^{+\infty} F(w) e^{jwt}dw \hspace{2cm}(傅里叶逆变换) \]

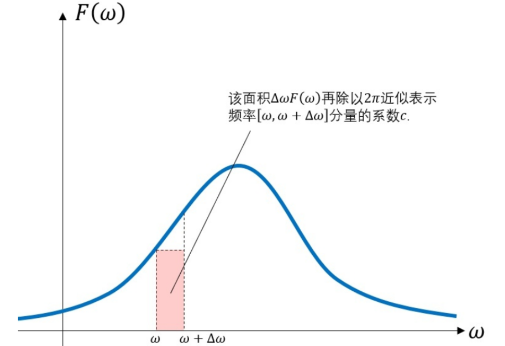
\(F(w)\)描述的就是\(f(t)在e^{-jwt}分量处的系数 · 2\pi(因为2\pi被提出去了)\), 是函数与在该正交分量相关性，通过\(f(t)\)得到F(w)的过程也被称之为傅里叶变换，\(F(w)\)又被称之为f(t)的频谱密度， 而对于原来的周期函数\(C_n\)，因为其分量的频率不是连续的，所以将\(c_n\)称为频谱(与概率分布函数和概率密度函数的概念一致)

离散时间傅里叶变换

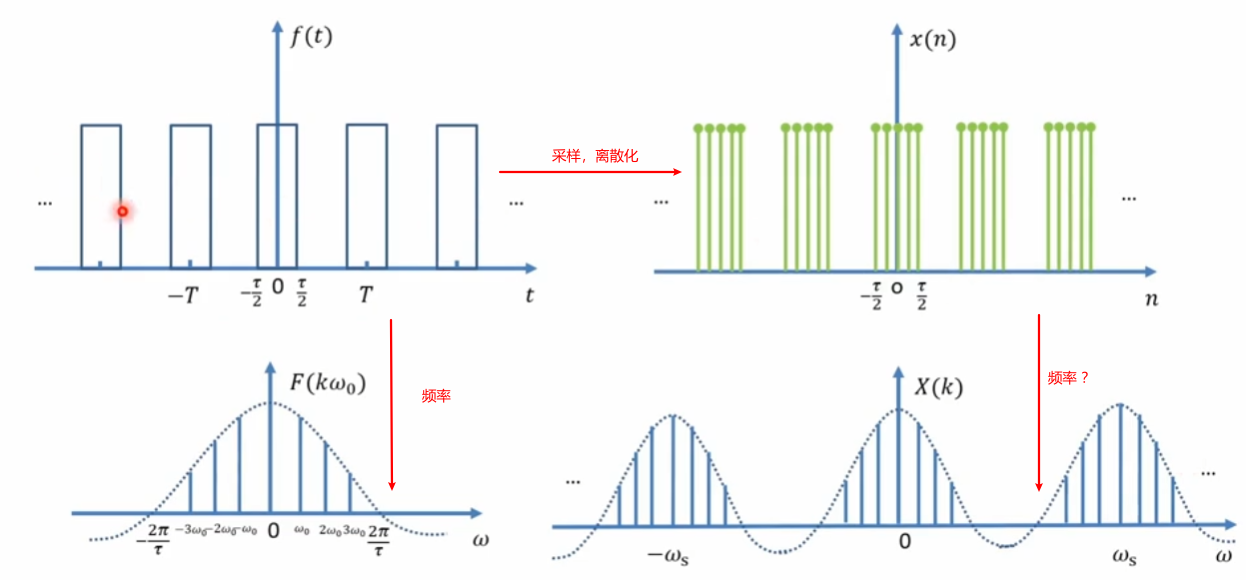
对于一个周期函数\(x(n)\)， 我们知道其傅里叶变换，但是如果对其进行采样后，它的频率的求解该怎么做呢？

它的公式如下：

\[离散时间傅里叶级数: \tilde{X}(k) = \sum_{n = 0}^{N -1} \tilde{x}(k) e^{-jk\frac{2\pi}{N}n} \\ 离散时间傅里叶级数逆变换: \tilde{x}(k) = \frac{1}{N} \sum_{k=0}^{N-1} \tilde{X}(k) e^{jk\frac{2\pi}{N}n} \]

离散时间傅里叶级数的公式很好理解，和傅里叶级数一样，就是计算投影的过程，但是现在函数点变成了取样点了\(\tilde{x}(k)\) 其它点都没有都是0，所以不用放过来； 然后基分量\(e^{-jk\frac{2\pi}{N}n}\)和过去的\(e^{-jtw_0n}\) 发生了形式上符号上发生了一点变化，但本质没有区别，右上角的构成仍然是虚数 · 自变量 · 角频率· 扩充倍数，唯一有变化的是角频率这个地方，其它都是一样的，角频率在这里被定义成了\(\frac{2\pi}{N}\), 而且N还是一个变量，表示的是取样点的数量，角频率\(w_0\)必须要和原函数保持一直，在这里取了\(N\)个点，它们可能如上图属于多个周期里面，也可能都在一个周期里面，那么这个时候角频率的范围就在\([\frac{2\pi}{N}, 2\pi]\)，所以就将角频率对在了最小的\(\frac{2\pi}{N}\)