从贝叶斯到卡尔曼滤波

1. 说明

本文是来自忠厚老实的老王在B站讲的卡尔曼滤波，经过自己理解写的总结笔记，课讲的非常好，一定要去听

2. 贝叶斯公式和应用

对于事件A和B，设其同时发生的概率为$P(A=a\bigcap B=b)$， 则存在：

$$P(A=a\bigcap B=b)=P(A=a|B=b)\ast P(B=b)=P(B=b|A=a)\ast P(A=a)$$

这是数学本质，A和B同时发生的概率为发生B的概率和在发生B时发生A的概率的乘积，很好理解。

$$P(A=a|B=b)=\frac{P(B=b|A=a)\ast P(A=a)}{P(B=b)}$$

经过变形可以得到，这就贝叶斯公式，

贝叶斯公式本质只是条件概率，如何基于这个公式对其进行应用呢？

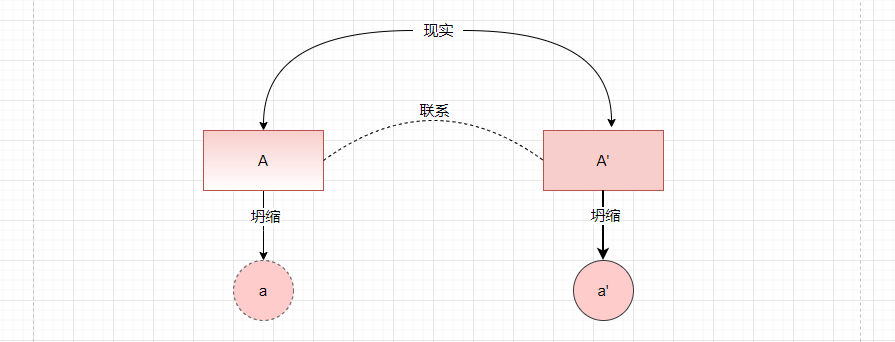
比如说测量现实温度，我们预设一个概率空间A对现实进行预测，我们当然可以通过加权积分的方式得到一个最终的预测值，但这个预设的概率空间的准确性很一般，这个时候，找到了一个它的影子A'，他们之间相关，而且状态空间A‘在现实中能够直接观测到一个结果a'，也就说明在这个现实下A’是朝着a'进行塌缩的，那么相对应的A会朝着相似的方向塌缩成a，所以只需要知道A， A‘， a'，还有A与A’之间的联系，就能够确定a了

• 举一个简单例子

有两个温度计A和B，要测量今天的温度，测得如下结果:

$P(A=10)=0.8,P(A=11)=0.2$

$P(B=10)=0.7,P(B=11)=0.2$

而且温度计B在出厂的时候测的和A的相关关系为:

$P(B=11|A=10)=0.3$

$P(B=10|A=10)=0.6$

现在，我们想要结合两个测量结果让结果更准确，让B去修正A，根据贝叶斯公式:

$P(A=10|B=10)=\frac{P(B=10|A=10)\ast P(A=10)}{P(B=10)}=\frac{0.6\ast 0.8}{0.7}=0.685$

当B=10的时候也就是说在一次观测中B这个系统朝着B=10这个方向塌缩了, 此时A也跟着塌缩P(A=10 | B= 10) =0.685, 和最初的$P(A=10)=0.8$相比就进一步收敛了，当然这里还遗留了一个问题：B=11的时候呢？这就属于另一个问题，多次观测的塌缩融合问题，后文另提

• 如何理解似然

  $P_{A|B}(a|b)=\frac{P_{B|A}(b|a)\ast P_A(a)}{P_B(b)}$ 通常为 $\mathrm{后}\mathrm{验}\mathrm{估}\mathrm{计}=\frac{\mathrm{似}\mathrm{然}\ast \mathrm{先}\mathrm{验}\mathrm{估}\mathrm{计}}{\mathrm{概}\mathrm{率}}$ ，

  其中$P_{B|A}(b|a)$叫做似然概率，表示事件a事件b发生的概率，这个值是一个固定值，只是表示的是A和影子状态B之前的相关性仅此而已，和$P_A(a)$大小无关，不会随着猜测$P_A(a)$的改变而改变，是一个预设值，表示两个系统的相关性。

3. 连续贝叶斯公式

在连续的概率分布中，只有单点概率密度而没有单点的概率，单点概率为0，但还是要计算概率为此要使用微分的思想化积为加，对于一个连续的贝叶斯概率$P(X<x|Y=y)$推导推导过程如下:

$$\begin{array}{rl}P(X<x|Y=y)& =\sum _{u=-\mathrm{\infty }}^{x}P(X=u|Y=y)\mathrm{化}\mathrm{连}\mathrm{续}\mathrm{为}\mathrm{累}\mathrm{加}\\ & =\sum _{u=-\mathrm{\infty }}^x\frac{P(Y=y|X=u)P(X=u)}{P(Y=y)}\mathrm{使}\mathrm{用}\mathrm{离}\mathrm{散}\mathrm{贝}\mathrm{叶}\mathrm{斯}\mathrm{公}\mathrm{式}\\ & =\underset{\epsilon \to \mathrm{\infty }}{lim}\sum _{u=-\mathrm{\infty }}^x\frac{P(y<Y<y+\epsilon |X=u)P(u<X<u+\epsilon )}{P(y<Y<y+\epsilon )}\mathrm{单}\mathrm{点}\mathrm{概}\mathrm{率}\mathrm{为}0，\mathrm{用}\mathrm{无}\mathrm{穷}\mathrm{小}\mathrm{量}\mathrm{表}\mathrm{征}\mathrm{连}\mathrm{续}\mathrm{性}\\ & =\underset{\epsilon \to \mathrm{\infty }}{lim}\sum _{u=-\mathrm{\infty }}^x\frac{(f_{Y|X}({\xi }_1|u)\times \epsilon )(f_X({\xi }_2)\times \epsilon )}{f_Y({\xi }_3)\times \epsilon }\mathrm{其}\mathrm{中}{\xi }_1\in (y,y+\epsilon ),{\xi }_2\in (u,u+\epsilon ),{\xi }_3\in (y,y+\epsilon )\\ & =\underset{\epsilon \to \mathrm{\infty }}{lim}\sum _{u=-\mathrm{\infty }}^x\frac{(f_{Y|X}(y|u))(f_X(u))}{f_Y(y)}\times \epsilon \mathrm{使}\mathrm{用}\mathrm{积}\mathrm{分}\mathrm{中}\mathrm{值}\mathrm{定}\mathrm{理}\\ & ={\int }_{-\mathrm{\infty }}^x\frac{(f_{Y|X}(y|u))(f_X(u))}{f_Y(y)}d(u)=>{\int }_{-\mathrm{\infty }}^x\frac{(f_{Y|X}(y|x))(f_X(x))}{f_Y(y)}d(x)(\mathrm{连}\mathrm{续}\mathrm{贝}\mathrm{叶}\mathrm{斯})\end{array}$$

最后的形式和离散贝叶斯很像，但是却变成了概率密度的相乘，多了个积分符号的dx, 其实很好理解，从推导的过程中可以知道，使用【概率密度*dx】代替【概率】后，分子分母约掉了一个dx，同时把整个x域的概率加起来

因为$f_Y(y)$可以通过全概率密度的方式计算出来，

$$f_Y(y)={\int }_{x=-\mathrm{\infty }}^{x=+\mathrm{\infty }}{f}_{Y|X}(y|x)f_X(x)dx$$

所以连续贝叶斯公式还有另一个形式

$$\begin{gathered} P(X<x|Y=y)={\int }_{-\mathrm{\infty }}^x\eta (f_{Y|X}(y|x))(f_X(x))d(x) \\ \mathrm{其}\mathrm{中}\eta =\frac{1}{f_Y(y)}=\frac{1}{{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}{f}_{Y|X}(y|x)f_X(x)dx} \end{gathered}$$

4. 贝叶斯滤波

在推导了连续的贝叶斯公式后，接下来就能够推导贝叶斯滤波算法，贝叶斯滤波基于贝叶斯概率的思想，首先对观测的建模得到预测方程，就能够基于前一个状态对下一个状态进行预测，同时对下一个状态进行观测得到预测方程，最终将两者融合后就能够得到一个比较准确的后验，整个过程如下所示:

---

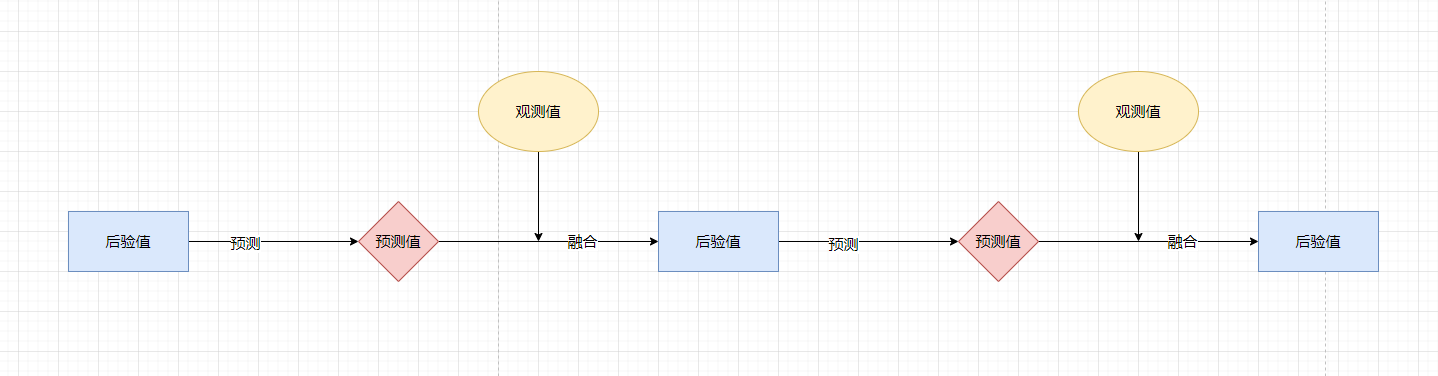
对于贝叶斯滤波算法的开始需要预测方程和观测方程

**预测方程：$$X_k=f(X_{k-1})+Q_K$$, **

**观测方程： $Y_k=h(X_K)+R_k$ **

$X_{k-1}:$ K-1时刻状态X的实际值
$X_k:$ K时刻状态X的预测值
$f:$ 前一状态和当前时刻的关系

$h:$ 实际值和观测值的关系

$Q_K:$ k时刻预测随机噪声

$R_k:$ k时刻的观测噪声

$Y_k:$ k时刻的观测值

其中： $X_0,Q_1,Q_2...Q_K,R_1,R_2....R_k$ 相互独立

并且有观测值： $y_1,y_2,...,y_n$

设$X_0$以及X的概率密度函数$f_{x0}(x)$, $Q_K$的概率密度函数$f_{Q_k}(x)$， $R_K$的概率密度函数$f_{R_k}(x)$

注意，此处的预测方程和观测方程中变量都是$X_k,Y_k$而不是$x_k,y_k$, 表示的还是一个范围下的随机变量；

---

• 如何理解预测方程和观测方程？

预测方程使用$f$做$ X_{k}$\mathrm{的}\mathrm{随}\mathrm{机}\mathrm{过}\mathrm{程}\mathrm{对}\mathrm{系}\mathrm{统}\mathrm{进}\mathrm{行}\mathrm{模}\mathrm{拟}\mathrm{建}\mathrm{模}，\mathrm{同}\mathrm{时}\mathrm{用}\mathrm{噪}\mathrm{声}$Q_{K}$去1.弥补建模的不准确。 2.模拟实际中存在的噪声

观测方程是在预测方程的基础上，使用$h$对预测出来的系统状态$X_k$做从系统状态到状态的转换，用$R_k$去模拟观测噪声

这个时候再回到贝叶斯思想的本身去看这两个方程，为了得到系统状态，利用随机过程对系统进行建模得到预测方程A，由于这个模型是不准的，为此找了与A有联系的影子A’，A‘能在现实中坍缩成a’，所以A也会朝着这个方向塌缩成a；$X_k$就是A， 而$Y_k$就是A’，要谨记它们不是一个具体的值，而是概率空间下的随机变量，$R_K$和$Q_K$是让两个系统成为概率空间的原因；此外将$X_K\mathrm{代}\mathrm{入}{Y}_k\mathrm{可}\mathrm{以}\mathrm{得}\mathrm{到}{Y}_k=h(f(x_{k-1}+R_k)+Q_K)$ , 提醒我们$Y_k\mathrm{与}{X}_K\mathrm{的}\mathrm{关}\mathrm{联}\mathrm{性}\mathrm{经}\mathrm{过}\mathrm{了}\mathrm{两}\mathrm{个}\mathrm{随}\mathrm{机}\mathrm{噪}\mathrm{音}{R}_k\mathrm{和}{Q}_K,\mathrm{所}\mathrm{以}\mathrm{成}\mathrm{了}\mathrm{概}\mathrm{率}\mathrm{关}\mathrm{系}$

---

• 推导过程

  $$\begin{gathered} \mathrm{目}\mathrm{标}\mathrm{式}:f_X^{+}(x)=\eta (f_{Y|X}(y|x))f_X^{-}(x) \\ \eta =\frac{1}{f_Y(y)}=\frac{1}{{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}{f}_{Y|X}(y|x)f_X(x)dx} \end{gathered}$$

  $f_X^{+}(x)$: x的后验概率密度也就是$f_{X|Y}(x|y)$的简略写法

  $f_X^{-}(x)$: x的先验概率密度，从观测方程得出

  y: 观测值y

此处的目标是只需要求出$f_X^{+}(x)$即可，有了概率密度函数后，后验x值使用积分$x_{}^{+}={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}x{f}_X^{+}(x)dx$计算可得

先验$f_X^{-}(x)$的推导，概率是概率密度的积分，要求概率密度，对概率求导即可

$$\begin{gathered} P(X_1<x)=\sum _{u=-\mathrm{\infty }}^{x}P(X_1=u) \\ \begin{array}{rl}P(X_1=u)& =\sum _{v=-\mathrm{\infty }}^{+\mathrm{\infty }}P(X_1=u|X_0=v)P(X_0=v)(\mathrm{全}\mathrm{概}\mathrm{率})\\ & =\sum _{v=-\mathrm{\infty }}^{+\mathrm{\infty }}P(X_1-f(X_0)=u-f(v)|X_0=v)P(X_0=v)\\ & =\sum _{v=-\mathrm{\infty }}^{+\mathrm{\infty }}P(Q_1=u-f(v)|X_0=v)P(X_0=v)\\ & =\sum _{v=-\mathrm{\infty }}^{+\mathrm{\infty }}P(Q_1=u-f(v))P(X_0=v)Q_1\mathrm{与}\mathrm{上}\mathrm{一}\mathrm{轮}\mathrm{的}X\mathrm{值}{X}_0\mathrm{独}\mathrm{立}\\ & =\underset{\epsilon \to 0}{lim}\sum _{v=-\mathrm{\infty }}^{+\mathrm{\infty }}{f}_{Q_1}(u-f(v))\cdot \epsilon \cdot f_{X_0}(v)\cdot \epsilon \mathrm{化}\mathrm{概}\mathrm{率}\mathrm{为}\mathrm{概}\mathrm{率}\mathrm{密}\mathrm{度}\\ & =\underset{\epsilon \to 0}{lim}{\int }_{v=-\mathrm{\infty }}^{+\mathrm{\infty }}{f}_{Q_1}(u-f(v))f_{X_0}(v)d(v)\cdot \epsilon \mathrm{将}\epsilon \mathrm{等}\mathrm{效}\mathrm{为}\mathrm{微}\mathrm{分}d(v)\end{array} \end{gathered}$$

$$\begin{array}{rl}\therefore P(X_1<x)& =\sum _{u=-\mathrm{\infty }}^{x}P(X_1=u)\\ & =\sum _{u=-\mathrm{\infty }}^{+\mathrm{\infty }}\underset{\epsilon \to 0}{lim}{\int }_{v=-\mathrm{\infty }}^{+\mathrm{\infty }}{f}_{Q_1}(u-f(v))f_{X_0}(v)d(v)\cdot \epsilon \\ & ={\int }_{-\mathrm{\infty }}^x{\int }_{v=-\mathrm{\infty }}^{+\mathrm{\infty }}{f}_{Q_1}(u-f(v))f_{X_0}(v)d(v)d(u)\end{array}$$

$$\therefore f_{X_1}^{-}(x)=\frac{d(P(X_1<x))}{dx}={\int }_{v=-\mathrm{\infty }}^{+\mathrm{\infty }}{f}_{Q_1}(u-f(v))f_{X_0}(v)d(v)(\mathrm{变}\mathrm{限}\mathrm{积}\mathrm{分}\mathrm{求}\mathrm{导})$$

---

似然$f_{Y|X}(y|x)$的推导, 思路也是一样，对概率取一个微积分空间然后求导

$$\begin{array}{rl}{f}_{Y_1|X_1}(y_1|x_1)& =\underset{\epsilon \to 0}{lim}\frac{P(y_1<Y_1<y_1+\epsilon |X_1=x)}{\epsilon }\\ & =\underset{\epsilon \to 0}{lim}\frac{P(y_1-h(x)<Y_1-h(X1)<y_1-h(x)+\epsilon |X_1=x)}{\epsilon }\\ & =\underset{\epsilon \to 0}{lim}\frac{P(y_1-h(x)<R_1<y_1-h(x)+\epsilon |X_1=x)}{\epsilon }\\ & =\underset{\epsilon \to 0}{lim}\frac{P(y_1-h(x)<R_1<y_1-h(x)+\epsilon )}{\epsilon }\mathrm{观}\mathrm{测}\mathrm{噪}\mathrm{声}{R}_1\mathrm{与}{X}_1\mathrm{独}\mathrm{立}\\ & =f_{R_1}(y_1-h(x))\end{array}$$

---

最后后验概率的值为:

$$\begin{gathered} f_1^{+}(x)={\eta }_1\cdot f_{R_1}[y_1-h(x)]\cdot f_{X_1}^{-}(x) \\ {\eta }_1=\frac{1}{f_{Y_1}(y)}=\frac{1}{{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}{f}_{R_1}[y_1-h(x)]f_{X_1}^{-}(x)dx} \end{gathered}$$

5. 卡尔曼滤波

**预测方程：$$X_k=F(X_{k-1})+Q_K$$, **

**观测方程： $Y_k=H(X_K)+R_k$ **

由于贝叶斯滤波的每一步推导都有无穷积分，而无穷积分解析解一般不存在导致贝叶斯滤波难以落地，为此做了两个：

1. f和h都假设为线性关系
2. $Q_k,R_k$假设为正态噪声服从$Q_k\mathrm{服}\mathrm{从}N(0,Q)，R_K\mathrm{服}\mathrm{从}N(0,R)$ ，这就是卡尔曼滤波

---

假设$X_{K-1}\mathrm{服}\mathrm{从}N(u_{k-1}^{+},{\sigma }_{k-1}^{+})$，先验$f_K^{-}(x)$的计算如下

$$\begin{array}{rl}{f}_{X_k}^{-}(x)& ={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}{f}_Q[x-f(v)]f_{X_{k-1}}^{+}(v)dv(1)\\ & ={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}(2\pi Q{)}^{-\frac{1}{2}}\cdot e^{-\frac{(x-Fv{)}^2}{2Q}}\cdot (2\pi {\sigma }_{k_{j-1}}^{+}{)}^{-\frac{1}{2}}\cdot e^{\frac{(v-u_{k-1}^{+}{)}^2}{2{\sigma }_{k-1}^{+}}}\cdot dv\end{array}$$

这个积分想要进一步化简并不容易，但仔细观察(1)参考此文可以发现这实质是$f_Q\mathrm{和}{f}_{X_{k-1}}^{-}$卷积的过程，时域的卷积就等于频域的乘积，可以通过傅里叶变化计算完后逆变换回来，最后计算得

$$\begin{gathered} f_{X_k}^{-}(x)\sim N(u_k^{-},{\sigma }_k^{-}) \\ {u}_k^{-}=F\cdot u_{k-1}^{+},{\sigma }_k^{-}=F^2{\sigma }_{k-1}+Q \end{gathered}$$

---

对于后验$f_{X_k}^{+}$

$$\begin{gathered} \begin{array}{rl}{f}_{X_k}^{+}& =\eta f_R(y_k-h\cdot x)\cdot f_{x_k}^{-}(x)\\ & =\eta (2\pi R{)}^{-\frac{1}{2}}\cdot e^{\frac{(y_k-hx{)}^2}{2R}}\cdot (2\pi {\sigma }_k^{-}{)}^{-\frac{1}{2}}\cdot e^{\frac{(x-u_k^{-}{)}^2}{2{\sigma }_k^{-}}}\end{array} \\ \eta =\frac{1}{{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}(2\pi R{)}^{-\frac{1}{2}}\cdot e^{\frac{(y_k-hx{)}^2}{2R}}\cdot (2\pi {\sigma }_k^{-}{)}^{-\frac{1}{2}}\cdot e^{\frac{(x-u_k^{-}{)}^2}{2{\sigma }_k^{-}}}} \end{gathered}$$

最后计算得到

$$\begin{gathered} \mathrm{最}\mathrm{后}\mathrm{计}\mathrm{算}\mathrm{得}\mathrm{到}{X}_k^{+}\sim N(u_k^{+},{\sigma }_k^{+}) \\ \mathrm{其}\mathrm{中}{u}_k^{+}=\frac{h{\sigma }_k^{-}{y}_k+R{u}_k^{-}}{h^2{\sigma }_k^{-}+R},{\sigma }_k^{+}=\frac{R{\sigma }_k^{-}}{h^2{\sigma }_k^{-}+R} \\ =>X_k^{+}\sim N(\frac{h{\sigma }_k^{-}{y}_k+R{u}_k^{-}}{h^2{\sigma }_k^{-}+R},\frac{R{\sigma }_k^{-}}{h^2{\sigma }_k^{-}+R}) \end{gathered}$$

令$k=\frac{h{\sigma }_k^{-}}{h^2{\sigma }_k^{-}+R}$, 则

$$\begin{gathered} u_k^{+}=u_k^{-}+k\ast (y_k-h{u}_k^{-}) \\ {\sigma }_k^{+}=(1-kh){\sigma }_k^{-} \end{gathered}$$

最终所有公式为

$$\begin{gathered} \mathrm{先}\mathrm{验}\mathrm{期}\mathrm{望}:u_k^{-}=F\cdot u_{k-1}^{+} \\ \mathrm{先}\mathrm{验}\mathrm{方}\mathrm{差}:{\sigma }_k^{-}=F^2{\sigma }_{k-1}+Q \\ \mathrm{后}\mathrm{验}\mathrm{期}\mathrm{望}:u_k^{+}=u_k^{-}+k\ast (y_k-h{u}_k^{-}) \\ \mathrm{后}\mathrm{验}\mathrm{方}\mathrm{差}:{\sigma }_k^{+}=(1-kh){\sigma }_k^{-} \\ \mathrm{其}\mathrm{中}：k=\frac{h{\sigma }_k^{-}}{h^2{\sigma }_k^{-}+R} \end{gathered}$$

会发现结果已经没有别的概率，只是期望和方差的加加减减，这是因为高斯函数的运算具有封闭性。

6. 矩阵形式的卡尔曼滤波

期望$u_k^{-}$变成了向量$\vec{u_{k}^{-}} $,\mathrm{方}\mathrm{差}$\sigma_{k}$\mathrm{变}\mathrm{成}\mathrm{了}\mathrm{协}\mathrm{方}\mathrm{差}\mathrm{矩}\mathrm{阵}$\Sigma_{k}$，关于正太分布中为什么方差变成了协方差矩阵参考多维高斯分布：

其中要特别注意，构建协方差矩阵时，不是用$X^2\mathrm{\Sigma }$,而是用$X^T\mathrm{\Sigma }X$这样的形式，因为这种形式算下来最后是一个1x1的值；

矩阵形式的卡尔曼滤波如下：小写的$\sigma ，h$变成了矩阵形式大写的$\mathrm{\Sigma }，H$, 1变成了单位矩阵$I$

$$\begin{gathered} \overrightarrow{u_k^{-}}=F\cdot \overrightarrow{u_{k-1}^{+}} \\ {\mathrm{\Sigma }}_k^{-}=F{\mathrm{\Sigma }}_{k-1}^{+}{F}^T+Q \\ \overrightarrow{u_k^{+}}=\overrightarrow{u_k^{-}}+k\ast (\overrightarrow{y_k}-H\overrightarrow{u_k^{-}}) \\ {\mathrm{\Sigma }}_k^{+}=(I-kH){\mathrm{\Sigma }}_k^{-} \\ \mathrm{其}\mathrm{中}:k=\frac{H{\mathrm{\Sigma }}_k^{-}}{H{\mathrm{\Sigma }}_k^{-}{H}^T+R} \end{gathered}$$

7. 应用

用来做系统预测的时候，一定会首先建模

**预测方程：$$X_k=F(X_{k-1})+Q_K$$, **

**观测方程： $Y_k=H(X_K)+R_k$ **

其中有一些要点，

1是F会导致预测模型是否能够拟合实际, 建模可以傻瓜式建模$X_k=X_{k-1}+Q_K$, 使用$Q_K$去做修正，但会不准确

2.是Q和R，观测值yk的出现后会R的大小会决定$Y_k$的塌缩程度，如果$R_k$小说明$Y_k$这个系统值很集中塌缩值要求很精确，所以要求输入得$X_k$也要塌缩的精确，这时候候$x_k^{+}$就更靠近 $y_k$，所以说我们更相信观测值；相反$R_K$大说明$Y_k$系统值塌缩得不准确，那么$X_k$塌缩得范围也大一些就会靠近自己得先验均值，这个时候就说$x_k^{+}$更靠近预测值

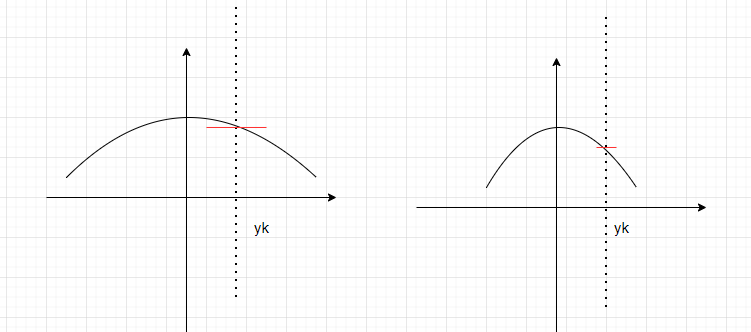
3.是预测值$X_0$的初值随便设置没关系的原因，X0设置的粗糙只是说系统一开始粗糙，但观测方程的塌缩，会让结果塌缩到正确的点，初值影响并不太大。