密码协议学习笔记(1.4):密码学的一些数学基础

数学基础:

抽象代数:

一个算符的代数结构:

幺半群:

数的集合和一个算符构成的代数结构$(G,+)$,且满足

• 封闭性
• 结合律
• 存在恒等元(在群中我习惯这么叫,避免混淆)

群:

满足如下条件的代数结构$(G,+)$:

• 封闭性
• 结合律
• 存在恒等元
• 对于每个元素均存在逆元

交换群/阿贝尔群:

满足如下条件的代数结构$(G,+)$.

• 封闭性
• 结合律
• 存在恒等元
• 对于每个元素均存在逆元
• 交换律

两个算符的代数结构:

环:

数的集合和两个算符构成的代数结构$(G,+,\cdot)$,且

• $(G,+)$是一个交换群
• $(G,\cdot)$是一个幺半群
• $\cdot$对$+$满足分配律

在环中,加法的恒等元记为$0$,也称零元,乘法的恒等元记为$e$或$1$

要求$(G,\cdot)$是幺半群而非群的理由是,$0$元素无法存在对$\cdot$的逆元

交换环:

数的集合和两个算符构成的代数结构$(G,+,\cdot)$,且

• $(G,+)$是一个交换群
• $(G,\cdot)$是一个满足交换律的幺半群
• $\cdot$对$+$满足分配律

域:

数的集合和两个算符构成的代数结构$(G,+,\cdot)$,且

• $(G,+)$是一个交换群
• $(G,\cdot)$是一个满足交换律的幺半群
• $\cdot$对$+$满足分配律
• $R \backslash \{0\}$对$\cdot$存在逆元

大佬博客上的一张图能直观说明这几个概念之间的联系:

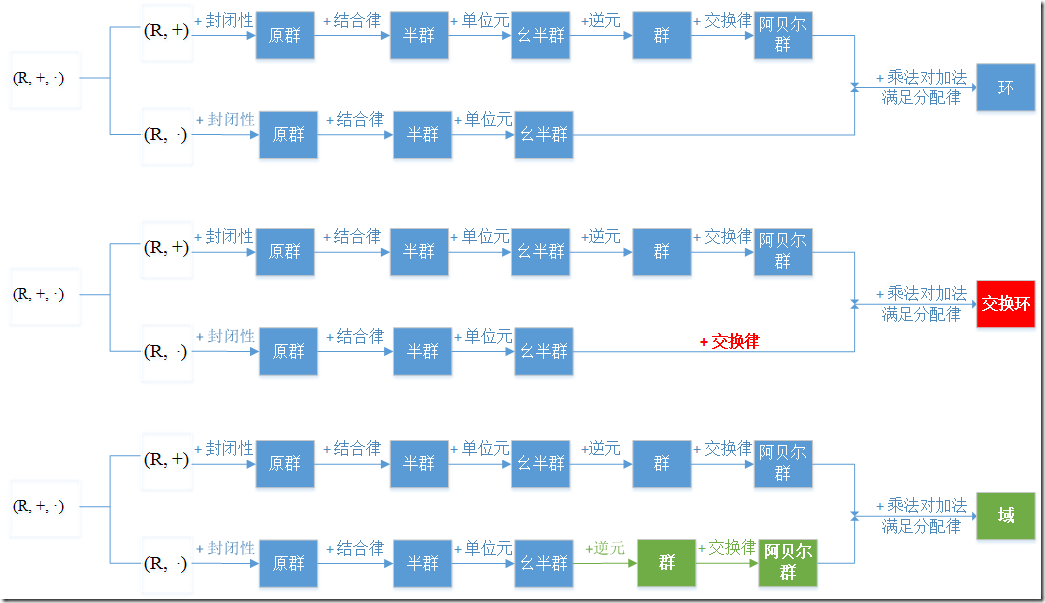
图源:http://sparkandshine.net/algebraic-structure-primer-group-ring-field-vector-space/

其他概念:

阶:

群,环,域等代数结构中,记$R$的大小为$|R|$.

循环群,循环子群,生成元:

设$(G,\cdot)$是群,$a\in G$,记 $(a)=\{a^i| i \in Z\}$,可以证明,$((a),\cdot)$为$(G,\cdot)$的子群,称$(a)$为由$a$生成的循环子群,并称$a$为该循环子群的生成元.

例如,$(\{1,3,5,7\},* \mod 8)$是一个群.

取$a=3$

$(3)=\{(1,3) * \mod 8\}$是由生成元$3$生成的循环子群

设$(G,\cdot)$是群,$a\in G$,若$a^n=e$,则对于那个最小的$n$,称$a$的阶为$n$.

可以证明,一个群中某元素的阶等于该生成元生成的循环子群的阶(即元素个数,这两个概念叫一个名字也是因为此).

若群$(G,\cdot)$中存在元素$a\in G$,其生成的循环子群$(a)$就是$(G,\cdot)$本身,那么称这个群为循环群,$a$为该群的生成元(注意,生成元未必是唯一的).

例如,$(\{1,2,4,5,7,8\},* \mod 9)$是一个循环群,使用$2$或$5$作为生成元能生成这个群本身,但使用$4$或$7$则只能生成$(\{1,4,7\},*\mod 9)$,使用$8$只能生成$(\{1,8\},*\mod 9)$,使用$1$则只能生成$(\{1\},*\mod 9)$.

可以证明,阶数相同的所有循环群相互之间均同构.

可以证明,素数阶群都是循环群,且非恒等元都是生成元.

例如,$(\{0,1,2,3,4,5,6\},+ \mod 7)$是循环群,$1,2,3,4,5,6$都是该群的生成元.

又例如,$(\{1,2,4,8,16,32,64\},* \mod 127)$是循环群,$1,2,4,8,16,32,64$都是该群的生成元.

这两个定理非常好用,每当遇到素数$p$阶的群$G$时可以构造出它与模加群$([0,p-1],+ \mod p)$之间的双射.

具体方法是找出它的恒等元$e$对应$0$,然后再随便揪出一个非恒等元$x$,令$x,x^2,x^3,\cdots,x^{p-1}$分别对应$1,2,3,\cdots,p-1$,这能大大减少思考问题的复杂度.

数论:

欧拉定理:

欧拉函数:

记为$\varphi(n)$,是$[1,n-1]$之间与$n$的最大公约数为$1$的数的个数.

可以证明,若$n=a_1^{x_1}\cdot a_2^{x_2} \cdots $,其中$a_1,a_2,\cdots$为$n$的质因数,那么$\varphi(n)=(a_1-1)\cdot a_1^{x_1-1} \cdot (a_2-1)\cdot a_2^{x_2-1} \cdots$

例如,$100=2^2\cdot 5^2$,那么$\varphi(100)=(2-1) \cdot 2^{2-1} \cdot (5-1) \cdot 5^{2-1}=40$,实际上,$[1,99]$中与$100$最大公约数为$1$的数有$1,3,7,9,11,13,17,19,21,23,27,29,31,33,37,39,41,43,47,49,51,53,57,59,61,63,67,69,71,73,77,79,81,83,87,89,91,93,97,99$,共计$40$个.

欧拉定理:

若$a,n$互质,则$a^{\varphi(n)}=1 \mod n$

费马小定理:

首先不难看出,若$n$为质数,则$\varphi(n)=n-1$

费马小定理本质上是欧拉定理的特殊形式,其形式为,若$n$为质数,那么任意$a\in[1,n-1]$,$a^{n-1}=1 \mod 1$,因此可以记$a^{n-2}=a^{-1} \mod n$,结合快速幂算法,这是一个计算模素数域的乘法逆元的简便方法.

原根:

阶:

回到欧拉定理,若$a,n$互质,则$a^{\varphi(n)}=1 \mod n$,可将$\varphi(n)$看作一个"循环节",但这个循环节并非最小循环节,例如,考虑$a=2,n=7$的情况,$\varphi(7)=6$,固然有$2^6=1 \mod 7$,但实际上,$2^3=1 \mod 7$,$3$才是$2$在模$7$下的"最小循环节",称$2$在模$7$意义下的阶为$3$.写作$\mathrm{ord}_7(2)=3$.

原根:

若某数$a$模$n$的阶恰好有$\mathrm{ord}_n(a)=\varphi(n)$,那么称$a$是$n$的一个原根.

有些数不存在原根,如$8$,$\varphi(8)=4$,但$1,2,3,4,5,6,7$模$8$的阶均不为$4$.

(主要参考资料:算法学习笔记(40): 原根 - 知乎 (zhihu.com))

根据Euler定理,若$gcd(a,m)=1$,则$a^{\varphi(m)}=1 (\mod m)$

若将$(1\mod m),(a \mod m),(a^2\mod m),(a^3\mod m),\cdots$看作一个数列,那么这个数列存在着一个长度为$\varphi(m)$的循环节,因为$a^{\varphi(m)}=1$.然而,这个循环节未必是最短的,比如当$a=2,m=7$时

$2^0=1,2^1=2,2^2=4,2^3=1,\cdots (\mod 7)$

循环节的长度就是$3$,而非$\varphi(7)=6$,将这个最短循环节的长度定义为$a$在模$m$下的阶,写作$ord_{m}a$,$ord_{7}2=3$(同时$2$也是$\varphi(7)=6$阶群上的一个$ord_{7}2=3$阶循环子群)

(考虑$ord_{m}a$的值和$m-1$阶循环群$([1,m-1],*\mod m)$里元素的个数的关系)

当$ord_{m}a=\varphi(m)$时,就称$a$为模$m$意义下的一个原根.(同时$a$也是$\varphi(m)$阶循环群自身的一个生成元)

并非所有模数都存在原根(并不是所有的群都是循环群),例如$\varphi(8)=4$,但$ord_{8}1=1,ord_{8}3=2,ord_{8}5=2,ord_{8}7=2$

实际上,对于原根存在性,有着如下的定理:

原根存在的性质:

正整数有原根的充要条件为:它能表示为下列形式之一:$2,4,p^n,2p^n$其中$p$为奇素数.

证明略.

原根的个数:

若$m$存在原根,则$m$的原根共有$\varphi(\varphi(m))$个,不妨记$a$是$m$的原根,那么对于任意与$\varphi(m)$互质的正整数$s$,$a^s$也是$m$的原根.

证明略.