Fine-Grained学习笔记(4):条件下界与归约,图论问题的复杂度归约理论

和P与NP问题一样,Fine-Grained领域中的许多问题也能相互归约,这意味着当这些问题中的任意一个问题的复杂度下界得到了证明或证伪,那么一系列问题的复杂度下界就都能够得到解决.

APSP猜想:

不存在$O(|V|^{3-\delta})$时间的(对于任意实数边权图都有效的)(确定性的)APSP算法.

APSP猜想的有限整数权值版本:

不存在$O(|V|^{3-\delta})$时间的,对于边权为$[U]$中元素的图的(确定性的)APSP算法.

(注意,Zwick算法是一个存在着得不到最优解的可能性的随机化算法.)

理论:

对于整数权值的情况:

APSP问题存在着$O(|V|^{3-\delta})$的算法,其中$\delta>0$

$\Leftrightarrow$ 最小权值三角形问题存在着$O(|V|^{3-\delta'})$的算法,其中$\delta'>0$

$\Leftrightarrow$ 图的半径问题存在着$O(|V|^{3-\delta''})$的算法,其中$\delta''>0$

问题:(min,+)矩阵乘的决定性问题版本:

给定$n\times n$的矩阵$A,B,D$,对于每一对$i,j$,判断是否$\exists k,a_{ik}+b_{kj}\leq d_{ij}$

问题:负权值三元环(NWT)问题:

给定三分边权图$G=(V=(X\cup Y\cup Z),E)$,记$O(|X|)=O(|Y|)=O(|Z|)=O(n)$,"三分"指的是图中点被划分成了三个不相交的集合$X,Y,Z$,同一集合中的点之间没有边:$E \subseteq (X\times Y)\cup (Y \cup Z) \cup (Z\cup X)$,如下图所示

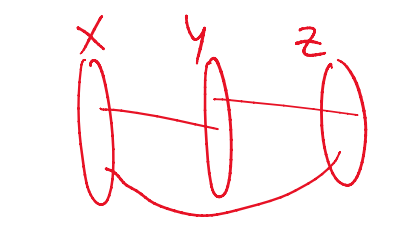
NWT的单解版本:

判断是否$\exists x\in X,y\in Y,z \in Z,w(x,y)+w(y,z)+w(z,x)\leq 0$,若是,则给出一组满足条件的$(x,y,z)$

NWT的全局解版本:

判断每条边$(z,x) \in (Z \times X) \cap E$,是否$\exists y,w(x,y)+w(y,z)+w(z,x)\leq 0$

NWT的决定性问题版本:

仅判断是否$\exists x\in X,y\in Y,z \in Z,w(x,y)+w(y,z)+w(z,x)\leq 0$并给出是或否

问题:图的半径:

对于(连通)图$G=(V,E)$,对于所有$v\in V$,记$rad(v)$为点$v$到其他点距离的最大值,找到点$v'$使得$rad(v')$的值最小,这个点称之为中心点,这个值即为图$G$的半径($rad(G)$)

问题:图的直径:

对于(连通)图$G=(V,E)$,找出所有$u,v\in V$中使得$d(u,v)$最小的$u',v'$,记$diam(G)=d(u',v')$

问题:零权值三元环(ZWT)问题:

给定三分边权图$G=(V=(X\cup Y\cup Z),E)$,$E \subseteq (X\times Y)\cup (Y \cup Z) \cup (Z\cup X)$,记$O(|X|)=O(|Y|)=O(|Z|)=O(n)$,判断是否$\exists x\in X,y\in Y,z \in Z,w(x,y)+w(y,z)+w(z,x)=0$

理论的证明:

方法:归约

(博主注:归约$A \to B$可以理解为拥有一个求解问题$B$的预言机(Oracle),然后使用这个预言机构造求解$A$的算法.)

归约APSP问题$\to$(整数无范围限制的)(min,+)矩阵乘问题:

假设(整数无范围限制的)(min,+)矩阵乘问题能在$O(n^{3-\delta})$时间内解决,其中$\delta>0$,那么,对于图$G=(V,E)$上的APSP问题,重复对$|V|\times |V|$的距离矩阵进行$\log |V|$次的矩阵乘法,时间复杂度$T(n)=O(|V|^{3-\delta}\cdot \log |V|) \leq O(|V|^{3-\delta'})$,其中$\delta'>0$

归约(有限整数范围下的)(min,+)矩阵乘$\to$(min,+)矩阵乘的决定性问题版本:

假设$n\times n$的,元素均在$[U]$范围内的(min,+)矩阵乘决定性问题能在$O(n^{3-\delta})$时间内解决,那么使用(min,+)矩阵乘的决定性问题模拟在矩阵的$n\times n$个点位上进行二分查找,共需$\log U$次,总时间复杂度$T(n)=O(n^{3-\delta}\cdot \log n) \leq O(n^{3-\delta'})$,其中$\delta'>0$

(min+)矩阵乘的决定性问题版本$\equiv$NWT问题的全局解版本:

对$A^{n\times n} \cdot B^{n\times n}$进行(min,+)矩阵乘并与$C^{n\times n}$进行比较的决定性问题版本中,$A,B$中的元素$a_{ik},b_{kj}$对应着$G=(V=(X\cup Y\cup Z),E)$的NWT问题全局解版本中,边$(x_i,z_k),(z_k,y_j)$的权值(若边不存在,则对应值为正无穷,即(min,+)矩阵乘在$i,j$点位的结果必定为否),$c_{ij}$对应着边$(x_i,y_j)$的权值的相反数(若边不存在,则对应值为负无穷,即(min,+)矩阵乘在$i,j$点位的结果必定为否).

归约NWT问题的全局解版本$\to$NWT问题的单解版本:

假设存在一个预言机能够在$T(n)=O(n^{3-\delta})$时间内,解决三分边权图$G=(V=(X\cup Y\cup Z),E)$上的NWT问题单解版本,为解决NWT问题的全局解版本,将点集$X,Y,Z$分别划分成大小为大小为$O(n/r)$的点集$X_1,\cdots,X_r,Y_1,\cdots,Y_r,Z_1,\cdots,Z_r$,

对于每组$i,j,k\in [r]$,进行以下步骤:

  重复进行以下内容直到退出:

    调用预言机以解决$X_i,Y_j,Z_k$上的NWT问题单解版本

    若存在可行解:

      将这个负三元环记录下来

      将这个负三元环从边集$E$中删除

      回到循环开始(再一次搜寻这一组$i,j,k$)

    若不存在可行解:

      退出循环(搜索下一组$i,j,k$)

返回记录下的所有负三元环

该程序最多需要调用预言机的次数为$r^3$(对每组$i,j,k$调用一次)$+k$(删去$k$组可行解),那么总的时间复杂度$T'(n)=O((r^3+k)T(n/r))\leq O((r^3+n^3)\cdot T(n/r))$,取$r=n^{2/3}$,$T'(n)=O(n^2\cdot T(n^{1/3}))\leq O(n^2 \cdot (n^{1/3})^{3-\delta})=O(n^{3-\delta/3})$

归约NWT问题的单解版本$\to$NWT问题的决定性版本:

假设存在一个预言机能够在$T(n)=O(n^{3-\delta})$时间内,解决三分边权图$G=(V=(X\cup Y\cup Z),E)$上的NWT问题决定性版本,为解决NWT问题的决定性版本,将点集$X,Y,Z$分别划分成大小为大小为$O(n/2)$的点集$X_1,X_2,Y_1,Y_2,Z_1,Z_2$

对于每组$i,j,k\in \{1,2\}$

  调用预言机判断在$X_i,Y_j,Z_k$中是否存在负三元环

  若存在:

    将$X_i,Y_j,Z_k$再重新各自折半拆分并递归调用该程序,直到$|X_i|=|Y_j|=|Z_k|=1$,此时便找到了负三元环.

  若不存在:

    继续搜索下一组$(i,j,k)$

算法的运行时间$T'(n)\leq T'(n/2)+8T(n/2)\leq O(n^{3-\delta})$

归约NWT$\to$图的半径问题:

假设图的半径问题可以在$T(n)=O(n^{3-\delta})$时间内解决,那么为了解决三分边权图$G=(V=(X\cup Y\cup Z),E)$上的NWT问题,取$M> \max_{e\in E}|w(e)|$,然后按如下的方式构造图$\hat{G}$:

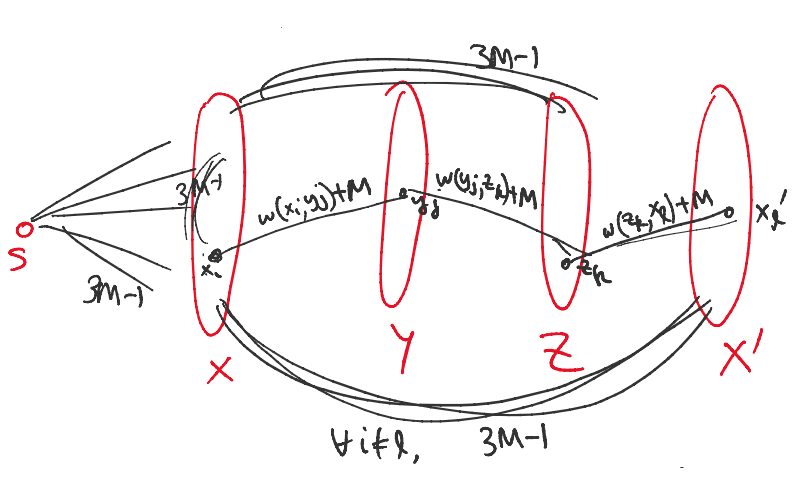
然后调用预言机在$T(O(n))\leq O(n^{3-\delta})$时间内计算该图的半径.

命题:

图$G$存在着负三元环$\Leftrightarrow$ $rad(\hat{G})<3M$

证明:

$\Rightarrow$:

若$G$中存在着负三元环$x_i,y_j,z_k$,那么$x_i$到其他点的距离必然均$<3M$.

$\Leftarrow$:

若$\hat{G}$的半径$<3M$,容易推出中心点必在$X$中,将其记为$x_i$,那么,$d(x_i,x'_i)<3M$,这意味着

$\exists y_j,z_k d(x_i,y_j)+d(y_j,z_k)+d(z_k,x'_i)$

$\Rightarrow$ 在图$G$中 $\exists y_j,z_k, (w(x_i,y_j)+M)+(w(y_j,z_k)+M)+(w(z_k,x_i)+M)<3M$

$ \Rightarrow w(x_i,y_j)+w(y_j,z_k)+w(z_k,x_i)<0$

便在$G$中找到了负三元环.

待解决的问题:APSP$\to$图的直径? 

引理:将不等转化为相等

给定三个整数$a,b,c$,$a+b+c>0$ $\Leftrightarrow$ $\exists i \lfloor \frac{a}{2^i} \rfloor + \lfloor \frac{b}{2^i} \rfloor + \lfloor \frac{c}{2^i} \rfloor \in \{1,2,3,4,5,6,7\}$ 

证明:

$\Leftarrow$:

若$\lfloor \frac{a}{2^i} \rfloor + \lfloor \frac{b}{2^i} \rfloor + \lfloor \frac{c}{2^i} \rfloor \in \{1,2,3,4,5,6,7\}$

$\Rightarrow \frac{a}{2^i}+  \frac{b}{2^i}  +  \frac{c}{2^i} $  

$\Rightarrow a+b+c>0$

$\Rightarrow$:

若$a+b+c>0$,

$\Rightarrow 2^{i+2}  \leq a+b+c < 2^{i+3} (i\geq 0)$

$\Rightarrow  4 \leq \frac{a}{2^i}+  \frac{b}{2^i}  +  \frac{c}{2^i} <8 $

$\Rightarrow  1 \leq \lfloor \frac{a}{2^i} \rfloor + \lfloor \frac{b}{2^i} \rfloor + \lfloor \frac{c}{2^i} \rfloor  \leq 7 $

归约(边权为有限整数的)NWT$\to$ZWT:

假设三分边权图的ZWT问题可以在$T(n)=O(n^{3-\delta})$时间内解决,那么,对于三分边权图$G=(V=(X\cup Y\cup Z),E)$,其中$E$中元素均$\in [-U,U]$,上的NWT问题,那么,根据以上引理

对于所有的$i \in [\log U]$:

  对于所有的$j=1,2,3,4,5,6,7$:

    在图$G'=(V=(X\cup Y\cup Z),E'=\{(u,v,\lfloor t*2^i \rfloor +j/3)|(u,v,t)\in E\})$上运行NWT的预言机,若找到零三元环则返回.

总时间复杂度为$O(T(n) \log U) \leq O(n^{3-\delta})$

总结:

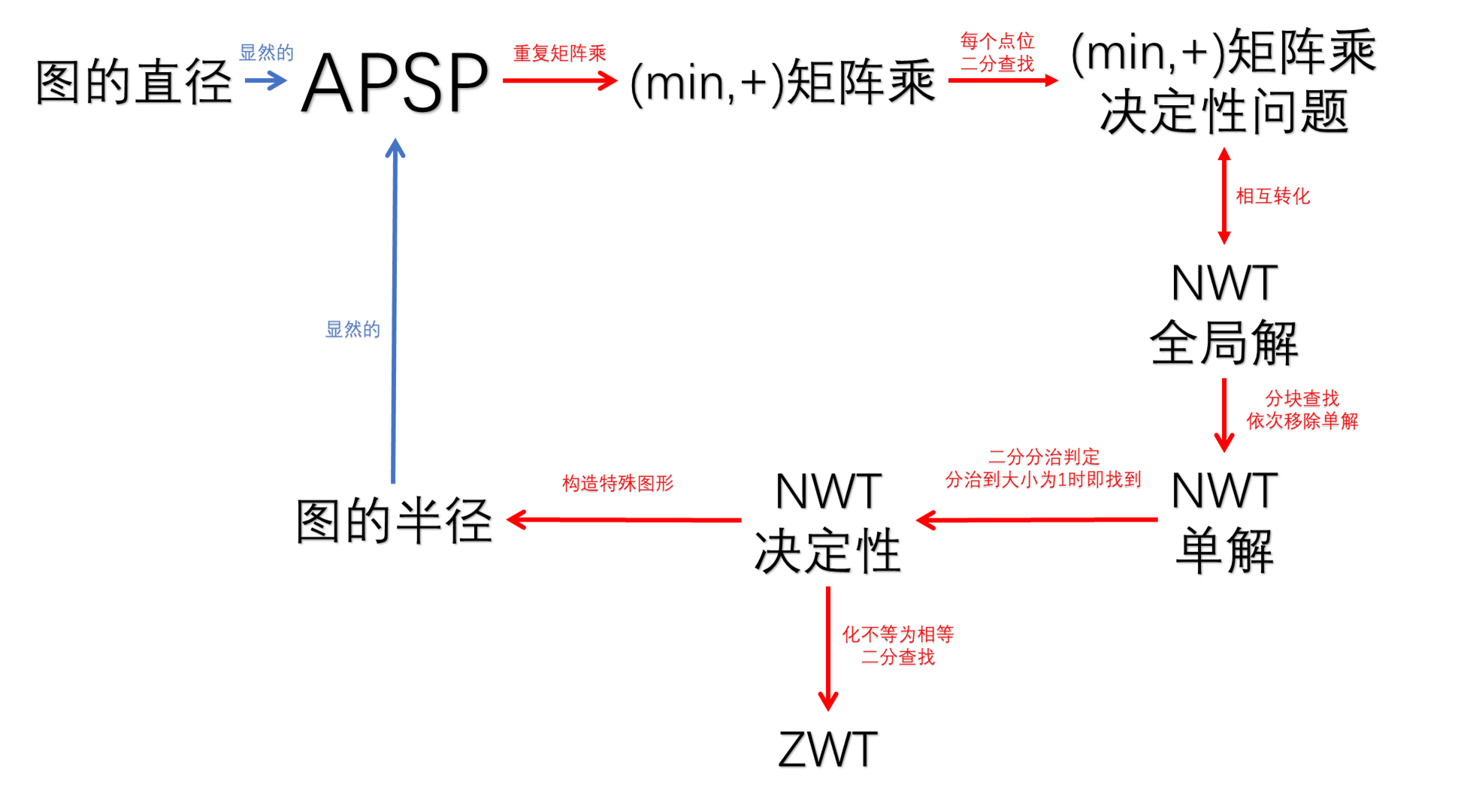
(博主注1:若能归约$A\to B$,即用$B$的预言机来构造$A$的算法,则若存在$B$的(限定复杂度的)算法,能够推出$A$也存在算法,反之未必.若$A$不存在算法,则能推出$B$也不存在算法,反之未必.)

(博主注2:因为归约过程中涉及了二分查找,在复杂度中引入了一个$\log U$的量,因此,图中所有问题的权值/矩阵元素最大值$U$中所包含的含$n$的项不能超过多项式级,才能保证$O(n^{3-\delta}\cdot \log U) \leq O(n^{3-\delta'})$)