Fine-Grained学习笔记(3):最短路(边权,点权),(min,+)矩阵乘
问题:APSP(全局最短路)
给定$G=(V,E)$,其中边集$E$带权值,对于$\forall s,t \in V$,计算$d(s,t)$,即从$s$到$t$的最小的经过路径权值之和
已知的算法:$n$次(堆优化的)Dijkstra算法:$\widetilde{O}(|V|\cdot|E|)$
Floyd-Warshall算法:$O(|V|^3)$
考虑如下的公式:
$c_{uv}^{(k)}=\min_{x\in V}(c_{ux}^{(k/2)} + c_{xv}^{(k/2)})$
形式上有些类似于矩阵乘,因此该过程被称为"(min,+)矩阵乘"
时间复杂度目前没有定论,但一般认为是$\Omega(n^{3-\epsilon})$时间(即不存在$O(n^{3-\epsilon})$的算法).
Zwick的最短路算法(2002):
引理(有限整数的(min,+)矩阵乘):
给定$n \times n$的矩阵$A,B$,其元素均包含于$[c] \cup \{\infty\}$之间(即要么是不连通边,要么权值小于等于常数),如此限制下,对$A,B$进行的(min,+)矩阵乘时间复杂度为$\widetilde{O}(cn^{\omega})$
证明:
按如下方式构造新的矩阵$A',B'$
$a'_{ij}=M^{a_{ij}} \qquad b'_{ij}=M^{b_{ij}}$,其中$M=n+1$为足够大的整数
然后使用普通的矩阵乘计算$C'=A'B'$
$c'_{ij}=\Sigma_{k=1}^{n}a'_{ik}b'_{jk}=\Sigma_{k=1}^nM^{a_{ik}+b_{kj}}$
总共需要进行$O(n^{\omega})$次$[M^c]$(位数为$O(c\log M)$)范围内的大整数运算,,每次大整数运算使用FFT消耗时间为$O(c\log M \cdot \log(c \log M))=\widetilde{O}(c)$
然后遍历矩阵中$n^2$个元素,对于矩阵的每个元素,用$O(c)$时间找到使得$c'_{ij} \geq M^{t}$的那个最大的$t$,即为$c_{ij}=\min_{x\in V}(a_{ik} + b_{kj})$的值
总时间复杂度为$\widetilde{O}(cn^{\omega})$,证毕.
然而,全局最短路可能有最多$O(|V|)$跳,若所有连通边权值不超过$c$,则最短路的距离可能为$O(c|V|)$,那么直接用(min,+)矩阵乘法进行重复矩阵乘以计算最短路矩阵,复杂度会上升到$\widetilde{O}(c|V|^{\omega+1})$,反倒比Floyd-Warshall算法更差了.
Zwick算法的第一个思路是根据跳数的多少对路径进行分类讨论
情况1:
跳数$\leq L$的最短路,进行$O(\log L)$次元素限制在$[cL]$内的(min,+)矩阵乘法,该情况下总时间复杂度$\widetilde{O}(cL|V|^{\omega})$
情况2:
跳数$\geq L$的最短路
碰撞引理:
随机选取$\exists R \subseteq V , |R|=O(\frac{|V|}{L} \log |V|)$,集合$R$能够概率性地与所有跳数$\geq L$的最短路"碰撞"($R$与某条路径"碰撞"指$R$中至少包含了路径中的一个点)
证明:
随机选取子集$R$,每个点被选中的概率均为$p=\frac{3}{L}\log |V|$
那么对于一组$s,t$,记$\Pi_{st}$为$s$到$t$的最短路所经过的边组成的集合,定理的描述中要求了$|\Pi_{st}|\geq L$,那么
$Pr[R \text{不与} \Pi_{st} \text{"碰撞"}] \leq (1-p)^{|\Pi_{st}|} \leq (1-p)^L \leq e^{-pL} \leq e^{-3\log |V|} =\frac{1}{n^3}$
那么,$Pr[\vee_{s,t \in V \text{且} \Pi_{st} \geq L|}(R \text{不与} \Pi_{st} \text{"碰撞"})] \leq |V|^2\cdot \frac{1}{|V|^3}=\frac{1}{|V|} $,证毕
在以此法找出的$R$上的所有点为原点,使用(堆优化的)Dijkstra算法,对正向边和反向边分别计算单源最短路,复杂度为$\widetilde{O}(|R|\cdot|E|)$,这样便得出了所有$r\in R, s,t \in V$的$d(s,r)$与$d(r,t)$
然后对于$\forall s,t \in V$,计算$d_{s,t} = \min_{r\in R}(d(s,r)+d(r,t))$,复杂度$O(|R|\cdot |V|^2)$
该情况下总时间复杂度$\widetilde{O}(\frac{|V|^3}{L})$
总的时间复杂度$\widetilde{O}(cL|V|^{\omega} + \frac{|V|^3}{L})$,取$L=\frac{n^{\frac{3-\omega}{2}}}{\sqrt{c}}$,得到$\widetilde{O}(\sqrt{c}n^{\frac{3+\omega}{2}}) \leq O(n^{2.687})$(在认为$c=O(1)$的前提下)
改进:对跳数较小的情况也应用碰撞引理
假设已经找到了所有跳数$\leq \frac{2l}{3}$的最短路,那么对于每个$V$中的点,以$p=\frac{l}{9}\log n$为概率选取每个点,将随机选取出的$\widetilde{O}(n/l)$个节点组成集合$R_{l/3}$,那么,$R_{l/3}$中元素未能与所有跳数$\in [l/3,(2l/3)]$的最短路"碰撞"上的概率$\leq 1/n $((1-p)^{|\Pi_{st}|}\leq (1-p)^{l/3} \leq 2^{-pl/3} \leq e^{-3\log n}=\frac{1}{n^3} n^2 \cdot \frac{1}{n^3} =\frac{1}{n} ),
在此概率化的条件下,以$R_{l/3}$中所有点为原点,使用(堆优化的)Dijkstra算法,对正向边和反向边分别计算单源最短路,得到所有$r\in R, s,t \in V$的$d(s,r)$与$d(r,t)$后,对于$\forall s,t \in V$,计算$d_{s,t} = \min_{r\in R_{l/3}}(d(s,r)+d(r,t))$.这样便能得到所有的跳数$\leq l$的最短路,示意图如下:
计算$d_{s,t} = \min_{r\in R_{l/3}}(d(s,r)+d(r,t))$的过程是一个对$|V| \times |R_{l/3}|$和$|R_{l/3}| \times |V|$的,元素值限制在$[O(cl)]$的两个长方形矩阵的(min,+)矩阵乘法,时间复杂度为$\widetilde{O}(cl\cdot M(|V|,|V|/l,|V|))$
无向边的情况:
Seidel在1995年证明了无权无向图最短路可在$\widetilde{O}(n^{\omega})$时间内解决
Galil,Margalit在1997年证明了边权值限制在$[c]$的情况下可在$\widetilde{O}(c^{\frac{\omega+1}{2}}n^{\omega})$时间内解决.
Shoshan,Zwick在1999年得到了$\widetilde{O}(cn^{\omega})$的算法
C.(作者本人),V.,Xu在2021年得到了更简便的$\widetilde{O}(cn^{\omega})$的算法
这里讲了一下作者本人的算法但因为我完全没明白,并且与主线关系也不大,所以就略过了
实数点权的最短路算法:
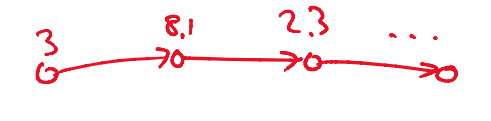
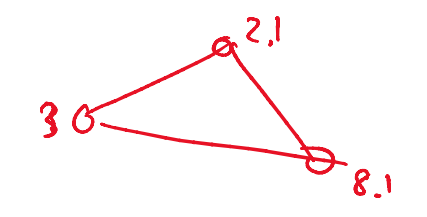
热身:在实数点权图中找出权值最小的三角形
引理:
给定$n\times n$的布尔矩阵$A,B$,计算"最小见证矩阵"$C$
$c_{ij}=\min\{k:a_{ik}\wedge b_{kj}\text{为真}\}$
的复杂度是$O(n^{2.529})$
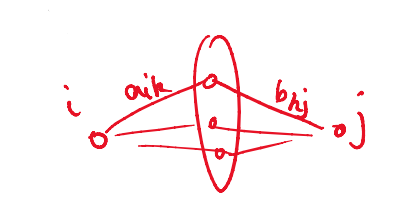
(可以理解为在下图中,对于每一对$i,j$,找到标号最小的,且与左点与右点均相连的中间点)
证明:(思路:分块)
将$[n]$拆分为$r$个长度为$n/r$的区间$I_1,\cdots,I_r$
步骤1:对于所有的$I_g(g \in \{1,\cdots,r\})$,计算$d_{ij}^{(g)}=\vee_{k \in I_g}(a_{ik}\wedge b_{kj})$,然后令$g_{ij}$为使得$d_{ij}^{(g)}$为最小的$g$
该步骤本质上是进行$r$次长方形矩阵乘法,复杂度为$O(r\cdot M(n,n/r,n))$
步骤2:根据得到的$g_{ij}$,暴力计算$c_{ij}=\vee_{k\in I_{g_{ij}}}(a_{ik}\wedge b_{kj})$
时间复杂度$O(n^2 \cdot \frac{n^2}{r})$
总时间复杂度$O(r\cdot M(n,n/r,n) + \frac{n^3}{r})=O(n^{2.529})$
Vassilevska,Williams,Yuster在2016年提出的最小点权三角形算法:
对于每一对$u,v$,计算$c_{uv}=\min\{w(x):(u,x)\in E \wedge (x,v) \in E\}$(将点$x$按权值排序之后运行"最小见证矩阵"算法,复杂度$O(n^{2.529})$)
然后在所有的$u,v$中,找出最小的$c_{vu}+w(u)+w(v)$
总时间复杂度$O(n^{2.529})$
Czumaj-Lingas在1990年对该问题提出了以递归的技巧达到的$\widetilde{O}(n^{\omega})$时间的算法.
回到APSP问题上来
引理:
给定实数矩阵$A\in R^{n\times n}$,矩阵$B\in \{0,\infty\}^{n \times n}$,那么这两个矩阵的(min,+)矩阵乘的运行时间为$O(n^{(3+\omega)/2}) \leq O(n^{2.687})$
实际上,就是在计算$c_{ij}=\min_{k: b_{kj} \neq \infty}\{a_{ik}\}$
证明:
将$A$的每一行进行排序并映射到$[n]$中,将$[n]$拆分为$r$个长度为$n/r$的区间$I_1,\cdots,I_r$
步骤1:
对于每个$I_g$,使用矩阵乘法在$O(rn^{\omega})$时间内计算$d_{ij}^{(g)}=\vee_k[a_{ik}\in I_g] \wedge [b_{kj}\neq \infty]$
然后令$g_{ij}=$使得$d_{ij}^{(g)}$最小的$g$
步骤2:
暴力计算$c_{ij}=\min_{a_{ik}\in I_{g_{ij}} ,b_{kj}\neq \infty} \{a_{ik}\}$
时间复杂度$O(n^2\cdot \frac{n}{r})$
总时间复杂度$O(rn^{\omega} + \frac{n^3}{r})=O(n^{\frac{3+\omega}{2}}))$(取$r=\frac{3-\omega}{2}$)
如果将步骤1的长方形矩阵乘法复杂度写作$O(M(rn,n,n))$,那么复杂度可以更精确地分析为$\widetilde{O}(n^{2.66})$
chan2007算法:
思路:根据跳数多少分类讨论
情况1:
跳数$\leq L$的最短路
假设所有跳数$\leq l-1$的最短路已找到
则计算$d^{(l)}(u,v)=(\min_{x \in V , (x,v)\in E} d^{(l-1)}(u,x))+w(v)$(使用前述引理,令$b_{xv}=\left\{\begin{matrix} 0 & (x,v) \in E \\ \infty & (x,v)\notin E\end{matrix}\right.$)
该情况的时间复杂度$O(Ln^{\frac{3+\omega}{2}})$
情况2:
跳数$\geq L$的最短路
将点权移动到边权上,然后同Zwick算法中的情况2,复杂度$\widetilde{O}(n^3/l)$
总时间复杂度$\widetilde{O}(Ln^\frac{3+\omega}{2}+\frac{n^3}{L})$
令$L=n^\frac{3-\omega}{4}$,$\widetilde{O}(n^{3-\frac{3-\omega}{4}})\leq O(n^{2.844})$
待解决的问题:更优的复杂度?实数边权(边权最短路问题比点权严苛,点权最多$|V|$个,边权最多$|E|=O(|V|^2)$个)?
