Fine-Grained学习笔记(2):矩阵乘法与图论
问题:矩阵乘法
方阵乘法:
给定两个$n \times n$的矩阵$A=(a_{ij}),B=(b_{ij})$,计算$C=AB,c_{ij}=\Sigma_{k=1}^na_{ik}b_{kj}$.
(由于语言习惯,本文中提到矩阵且无其他说明的场合,均指方阵)
朴素算法的复杂度:$O(n^3)$
设想中的复杂度下界:$\Omega(n^2)$(把$n\times n$的矩阵读取完就需要$O(n^2)$时间了)
Strassen算法(1969):
热身:考虑$n=2$的情况:
$c_{11}=a_{11}b_{11}+a_{12}b_{21}$
$c_{12}=a_{11}b_{12}+a_{12}b_{22}$
$c_{21}=a_{21}b_{11}+a_{22}b_{21}$
$c_{22}=a_{21}b_{12}+a_{22}b_{22}$
共需$8$次乘法
思路:
考虑
$p_1=a_{11}(b_{11}-b_{21})$
$p_2=(a_{11}+a_{12})b_{21}$
$p_3=a_{22}(b_{22}-b_{12})$
$p_4=(a_{21}+a_{22})b_{12}$
$p_5=(a_{11}+a_{22})(b_{21}+b_{12})$
$p_6=(a_{12}-a_{22})(b_{21}+b_{22})$
$p_7=(a_{21}-a_{11})(b_{11}+b_{12})$
$c_{11}=p_1+p_2$
$c_{12}=p_5+p_6+p_3-p_2$
$c_{21}=p_5+p_7+p_1-p_4$
$c_{22}=p_3+p_4$
总共只需要进行$7$次乘法.
然后考虑任意$n$的情况,将$A,B$划分为四个子矩阵
$A=\begin{bmatrix}A_{11} &A_{12} \\A_{21} &A_{22}\end{bmatrix}$
$B=\begin{bmatrix}B_{11} &B_{12} \\B_{21} &B_{22}\end{bmatrix}$
并进行递归分治,分析时间复杂度
$T(n)=7T(n/2)+O(n^2)$
$T(n)=O(n^{\log_2 7}) \leq O(n^{2.81})$
其他的分治法思路
Laderman在1976年证明了$3\times 3$的矩阵乘法只需进行$23$次乘法运算,然而对矩阵乘进行三路分治的复杂度$T(n)=23T(n/3)+O(n^2)=O(n^{\log_2 23})\leq O(n^{2.85})$,反倒不如二路分治
Pan在1978年证明了$k=70$的矩阵乘法共需$\frac{k^3-4k}{3}+6k^2=143640$次乘法,因此对矩阵乘法进行$70$路分治的复杂度$T(n)=143640T(n/70)+O(n^2)=O(n^{\log_{70} 143640})\leq O(n^{2.796})$
Pan又在1978年证明了$k=46$的矩阵乘法共需$41952$次,因此对矩阵乘法进行$46$路分治的复杂度为$T(n)=41952T(n/46)+O(n^2)=O(n^{\log_{46}41952})\leq O(n^{2.781})$
Bini等人在1980年使用"Border Rank"理论使得矩阵乘法复杂度降低到了$O(n^{2.780})$
Schonhage在1981年矩阵乘法复杂度降低到了$O(n^{2.522})$
Strassen在1986年使用"Laser Method"将矩阵乘法复杂度降低到了$O(n^{2.479})$
$\vdots$
目前对矩阵乘法的复杂度下界尚没有一个定论,在本文中使用$O(n^{\omega})$表示矩阵乘法的复杂度,并认为$\omega=2.372$.
(长方形)矩阵乘法:
给定$n_1 \times n_2$的矩阵$A=(a_{ij})$,$n_2\times n_3$的矩阵$B=(b_{ij})$,计算$n_1\times n_3$的矩阵$C=AB,c_{ij}=\Sigma_{k=1}^na_{ik}b_{kj}$.
记$M(n_1,n_2,n_3)$为进行该运算所需的时间复杂度,记$\omega(a,b,c)=\log_n(M(n^a,n^b,n^c))$
以下结论是显然的:
1,$\omega(\cdot,\cdot,\cdot)$是凸函数
$\omega(ta_1+(1-t)a_2,tb_1+(1-t)b_2,tc_1+(1-t)c_2)\leq t\omega(a_1,b_1,c_1)+(1-t)\omega(a_2,b_2,c_2), \forall t \in[0,1]$
2,$\omega(\cdot,\cdot,\cdot)$是对称的
$\omega(a,b,c)=\omega(c,b,a)=\cdots$
简单的下界性质:
考虑$M(n,l,n)$形式的问题,根据$l,n$之间的大小关系,将矩阵分为两种情况,根据矩阵乘法中左侧的矩阵的形状,将这两种情况称为"瘦矩阵"和"扁矩阵"
瘦矩阵乘:
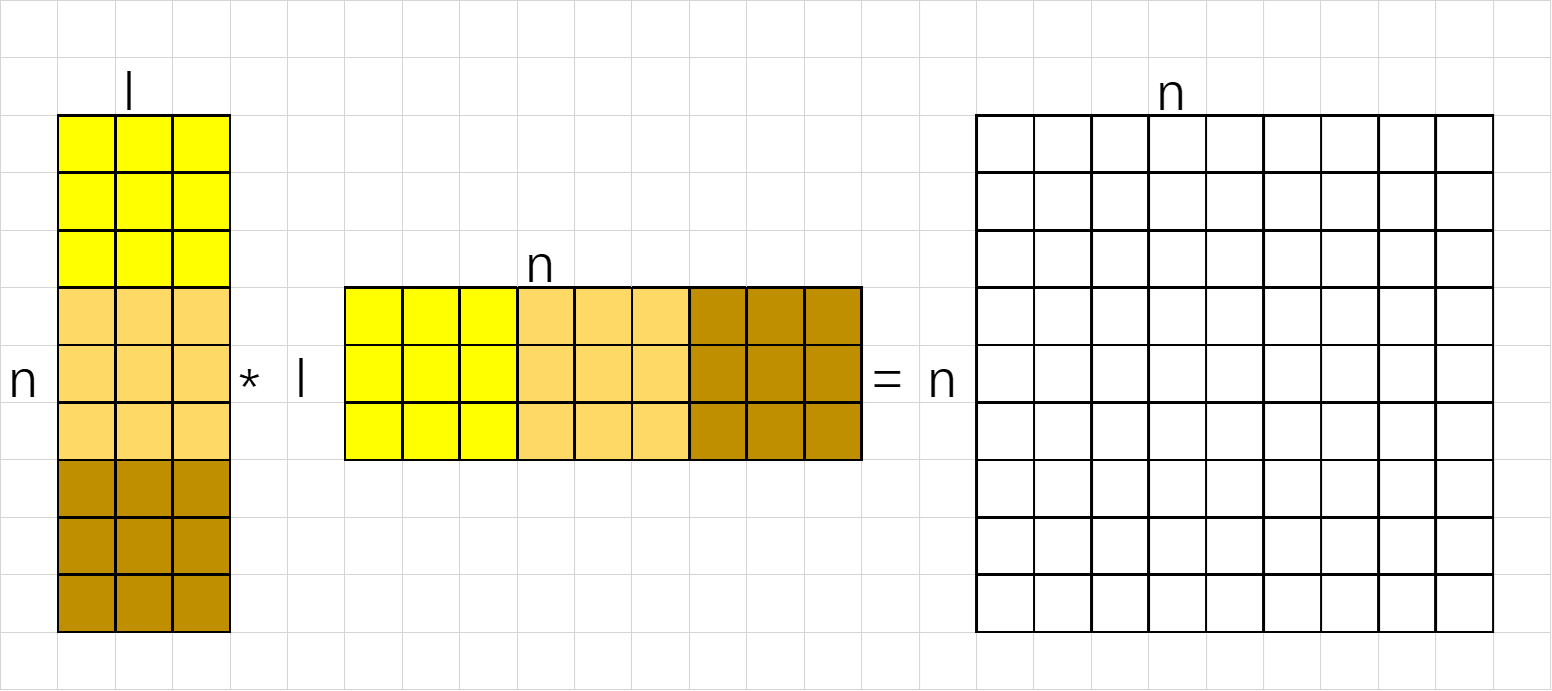
按照如上方式,将两个矩阵分别拆分成$n/l$个$l \times l$的矩阵,总时间复杂度为$O((n/l)^2l^{\omega})=O(l^{\omega-2}n^2)$
扁矩阵乘:
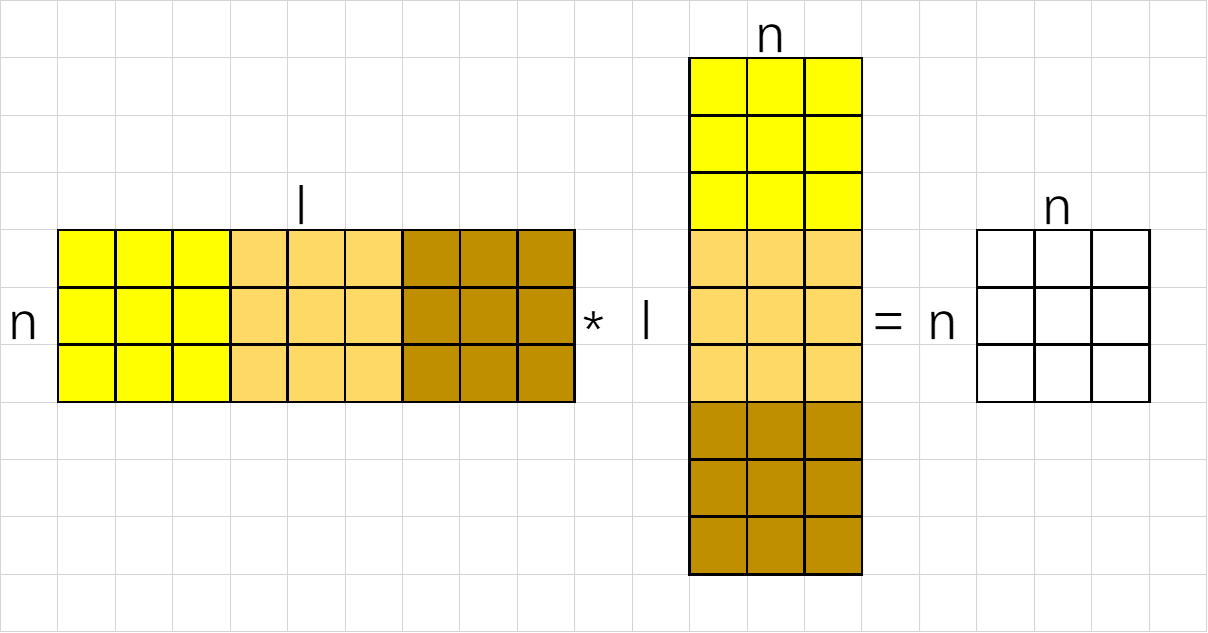
按照如上方式,将两个矩阵分别拆分成$l/n$个$n \times n$的矩阵,总时间复杂度为$O((l/n)l^{\omega})=O(ln^{\omega-1})$
但实际上,针对这两种分类还有更好的算法:
对于瘦矩阵乘:
Coppersmith在1982年给出了$M(n,n^{0.172},n)=\widetilde{O}(n^2)$的结论
LeGall和$Urrutia$在2018年给出了$M(n,n^{0.3189},n)=O(n^{2+\epsilon})$的结论
对于扁矩阵乘:
当$k>1,M(n,n^k,n)=O(n^{k+1+f(k)})$,其中,当$k\to \infty$时,$f(k)\to 0$
稀疏矩阵乘:
对于两个$n\times n$的矩阵$A,B$,其中的非零元素为$m$个,$m\ll n^2$
朴素算法:
复杂度为O(mn),由于$m\ll n^{\omega-1}$,因此优于$O(n^{\omega})$
博主注:这个$O(mn)$的算法是怎么样的我没有想明白,感觉并不是那么朴素.
Yuster和Zwick的算法(2005):
思路:按照矩阵$A$中每列非零元素个数多少,将所有列分为高频和低频两类讨论
记$deg(k)=|\{i:a_{ik}\neq 0\}|$
$H=\{k:deg(k) > \Delta\}$
$L=\{k:deg(k) \leq \Delta\}$
这样便保证了$|H|\leq m/\Delta$
低频列:
计算$c^L_{ij}=\Sigma_{k\in L}a_{ik}b_{kj}$,具体的方法是:
$\text{对于所有使得$b_{kj} \neq 0$的$k,j: \qquad$ (循环次数$O(m)$)} $
$\qquad \text{对于所有使得$a_{ik}\neq 0$的$i: \qquad$ (循环次数$O(\Delta)$) }$
$\qquad \qquad c_{ij}+=a_{ik}b_{kj}$
该情况时间复杂度$O(m\Delta)$
高频列:
将$H$中所对应的矩阵$A$中的列和矩阵$B$中的行提取出来,构造出两个长方形矩阵:$n\times |H|$的矩阵$A'$,$|H|\times n$的矩阵$B'$,计算$A'\cdot B'$,得到$c^H_{ij}=\Sigma_{k\in H}a_{ik}b_{kj}$,该情况时间复杂度$M(n,m/\Delta,n)$
总时间复杂度$O(m\Delta+M(n,m/\Delta,n))$
应用:与矩阵和线性代数有关的问题
矩阵求逆,$Ax=b$线性方程求解......
应用:有向图中寻找三元环
给定有向图$G=(V,E)$
判断是否存在三个点$u,x,v \in V$,使得$(u,x),(x,v),(v,u) \in E$
朴素算法:
(1)暴力枚举三个点,时间复杂度:$O(|V|^3)$
(2)枚举所有边$(v,u)$,再枚举第三个点$x$,判断$(u,x),(x,v)$是否存在,时间复杂度:$O(|V|\cdot |E|)$,在$|E|\ll |V|^2$的稀疏图中较优
(3)利用矩阵乘法:
对于所有的$u,v\in V$,计算$c_{u,v}=\vee_{x\in V}(\{(u,x)\in V\} \wedge \{(x,v \in V)\})$,可由矩阵乘法计算.
然后对于所有$u,v$,判断$c_{uv}=1 \wedge (v,u)\in E$
总时间复杂度$O(|V|^{\omega})$,相比算法(2)更适用于稠密图.
(4)利用稀疏矩阵乘法,复杂度$O(|E|\Delta+M(|V|,|E|/\Delta,|V|))$
Alon,Yuster,Zwick的算法(1997):
思路还是分为高低频,根据点的度数划分(算法描述中使用的是点的出度)
$H=\{v\in V:deg(v) > \Delta\}$
$L=\{v\in V:deg(v) \leq \Delta\}$
情况1:
部分点在$L$中的三角形,不妨记$x\in L$
$\text{对于所有使得$(u,x) \in E$的$u,x$: $\qquad$(循环次数$O(|E|)$)} $
$\qquad \text{对于所有使得$(x,v) \in E$的$v:$ $\qquad$ (循环次数$O(\Delta)$)}$
$\qquad \qquad \text{判断是否有} (v,u)\in E$
该情况的时间复杂度:$O(|E|\Delta)$
情况2:
三个点都在$H$中的三角形
注意,$|H|\leq |E|/\Delta$
运行朴素算法(3),该情况时间复杂度$O((|E|/\Delta)^{\omega})$
总时间复杂度:$O(|E|\Delta + (|E|/\Delta)^{\omega})$
取$\Delta=|E|^{\frac{\omega-1}{\omega+1}}$,因为前文约定了$\omega=2.372$,
得到$O(|E|^{\frac{2\omega}{\omega+1}})\leq O(|E|^{1.41})$
应用:有向图中寻找$k$元环($k$为常数)
Alon,Yusher,Zwick:Color coding,时间复杂度$O(|V|^{\omega})$,具体算法待查
对于稀疏图:
$k=4:O(|E|^{1.48})$
$\vdots$
应用:$k$-Clique($k$团)
在无向图中寻找$k$个两两相连的点构成的子图,$k$为常数
暴力枚举:$O(|V|^k)$
若$k \mod 3=0$,则可用$O(|V|^{k/3})$时间暴力枚举出图中的所有$k/3$团,将所有$k/3$团作为超级节点加入新点集$V'$中,$|V'|=O(|V|^{k/3})$,然后对于所有的$A,B \in V'$,若$A$在$G$中对应的点,均有指向$B$在$G$中对应的点,则将边$(A,B)$加入新边集$E'$中,这样,问题就变为了在$G'=(V',E')$上寻找三元环的问题,总时间复杂度$O((|V|^{k/3})^{\omega})$
应用:带权图
定义:(min,+)矩阵乘
$c_{uv}=\min_{x\in V}(a_{ux}+a_{xv})$
类似于最短路算法中的"松弛"操作
下一章将会讨论这个算法
应用:传递闭包(全局连通性)
给定有向图$G=(V,E)$,判断对于$\forall s,t \in V$,是否存在从$s$到$t$的路径
朴素算法:
(1)进行$|V|$次DFS/BFS:$O(|V|\cdot|E|) \leq O(n^3)$
(2)Warshall DP(类似于Floyd):枚举中点$x \in V$,再枚举两端点$u,v\in V$,若边$(u,x),(x,v)$均存在,则将边$(u,v)$加入边集$E$中,时间复杂度$O(n^3)$
Warshall算法使用重复矩阵乘的改进:
记$c_{uv}^{(k)}$为真,当且仅当存在一条$\leq k$跳的,从$u$到$v$的路径.
对于$k=1,2,4,\cdots,|V|$,用矩阵乘法计算$c_{uv}^{(k)}=\vee_{x\in V}(c_{ux}^{(k/2)}\wedge c_{xv}^{(k/2)})$
总时间复杂度:$O(||^{\omega} \log |V|) \leq O(|V|^{2.373})$
Munro算法(1971):
考虑$G$是一个DAG(有向无环图)的情况,对于任意的图,可以通过搜索出所有强连通分量并合并为超级节点做到这一点.
搜索强连通分量并缩点的方法是Tarjan算法,一种DFS算法,在DFS的过程中将搜索到的顺序作为时间戳标记在每个节点上,并记录从该点回溯能够到达的时间戳最小的节点.在许多博客都有相应的讲解,这里不再赘述.
这样做的意义在于,DAG保证了邻接矩阵必定是一个上三角矩阵,记$A=(a_{ij}),a_{uv}$为真,当且仅当$u$到$v$之间有一条边,$A^{*}=(a^{*}_{ij}),a^{*}_{uv}$为真,当且仅当$u$到$v$之间存在着连通的路径.
将$A$写成如下分块矩阵的形式:
$A=\begin{bmatrix}A_{11} &A_{12} \\0 & A_{22}\end{bmatrix}$
那么
$A^{*}=\begin{bmatrix}A^{*}_{11} &A^{*}_{11}A_{12}A^{*}_{22} \\0 & A^{*}_{22}\end{bmatrix}$
由于$A_{11},A_{22}$也是上三角矩阵,因此可以递归求解,矩阵维数为$1$时,$A^{*}_{11}=A_{11},A^{*}_{22}=A_{22}$,因此总复杂度$T(n)=2T(n/2)+O(n^{\omega})$,复杂度相比重复的矩阵乘减少了一个对数项.
