FFT(快速傅立叶变换)学习
主要参考资料:3b1b的视频快速傅里叶变换(FFT)——有史以来最巧妙的算法?_哔哩哔哩_bilibili在此一并感谢字幕制作者
FFT只有一个功能:快速计算卷积,它能把朴素卷积的$O(n^2)$时间复杂度降低到$O(nlogn)$。
卷积:
卷积就是把两个离散序列的每一位两两相乘的过程,多项式的乘法就是一种卷积。
假如两个序列x,y,卷积之后的结果是z,那么z的某一位是这样表示的:
$z(n)=\sum_{i=-\infty}^{+\infty}x(i)\cdot y(n-i)$
通过这个式子可以看出,如果x,y这两个序列有n个元素,那暴力计算卷积的时间复杂度是$O(n^2)$的
系数表示法与点值表示法:
那么,怎样快速计算卷积呢,这需要从多项式的两种表示方法说起。
比如两个多项式$f_1(x)=x^3+2x^2+3x+4$和$f_2(x)=4x^3+3x^2+2x+1$
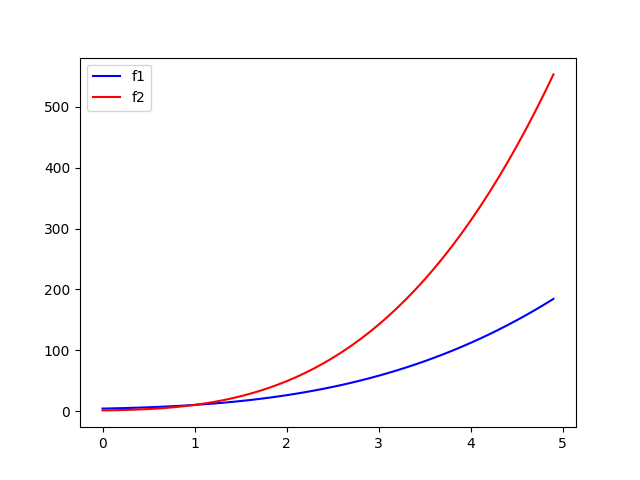
可以直接把它们每一项的系数拿出来,$\{1,2,3,4\}$,$\{4,3,2,1\}$这就是系数表示法。
也可以在x-y平面上,把这个多项式看作曲线,找几个这个曲线经过的点,多项式是k次的,那它在平面上对应的曲线就能被k+1个点唯一确定。
$\{(0,4),(1,10),(2,26),(3,58)\}$
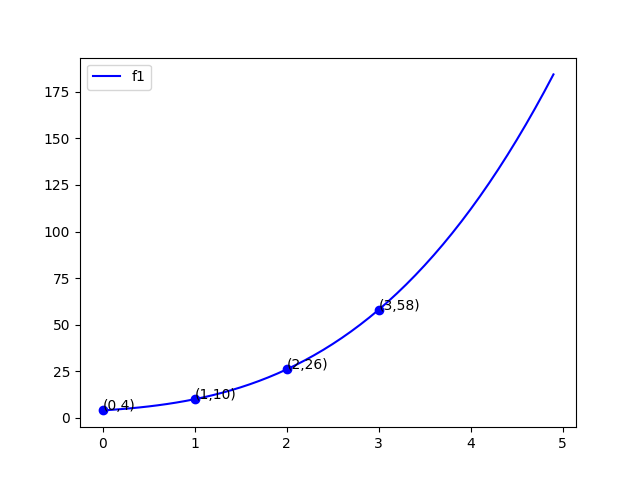
$\{(0,1),(1,10),(2,49),(3,142)\}$
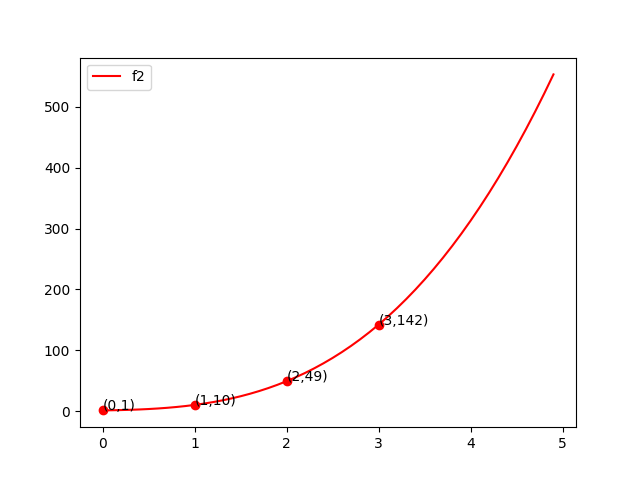
这就是点值表示法
把系数表示法变换为点值表示法叫点值运算,把点值表示法变换为系数表示法叫插值运算。
因为两个多项式卷积起来是一个6次多项式,所以要分别在它们对应的曲线上找7个点。
$\{(0,4),(1,10),(2,26),(3,58),(4,112),(5,194),(6,310)\}$
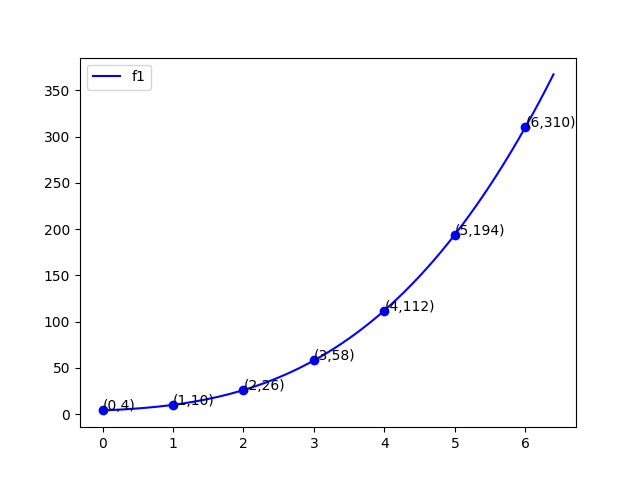
$\{(0,1),(1,10),(2,49),(3,142),(4,313),(5,586),(6,985)\}$
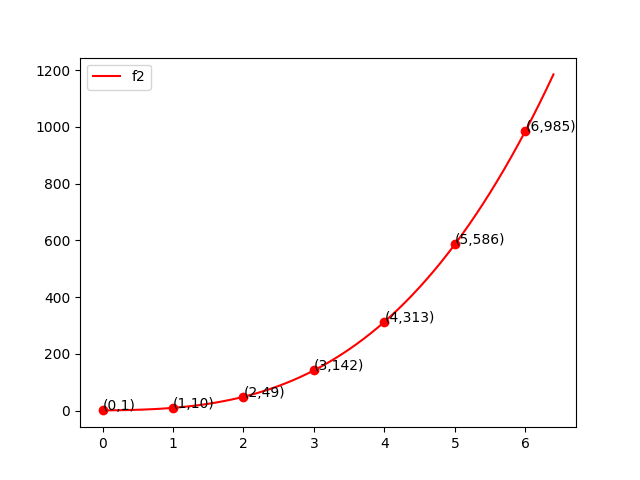
把相同横坐标对应的纵坐标乘起来,就是点值表示法的卷积计算了。
$\{(0,4),(1,100),(2,1274),(3,8236),(4,35056),(5,113684),(6,305350)\}$
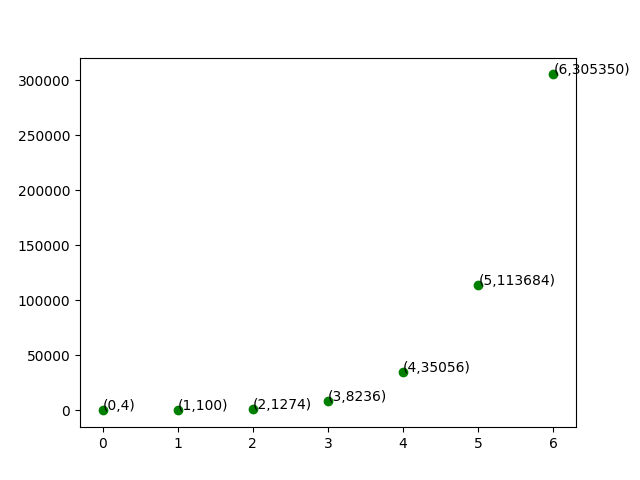
(将点值表示法转化为系数表示法的方法,常用的方法是拉格朗日插值,具体可参考Lagrange插值 - Isakovsky - 博客园 (cnblogs.com),这里略)
使用$O(n^2)$暴力卷积的方式计算多项式
$4x^6+11x^5+20x^4+30x^3+20x^2+11x+4$
代进去验算,果然没错,这样,只用7次乘法,也就是O(n)时间,就完成了点值表示法下的多项式乘法计算。
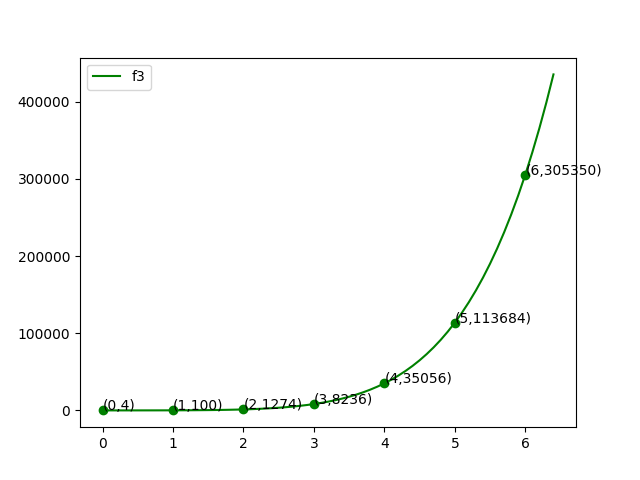
但是将单个横坐标$x$值代进系数表示法中并求值需要算出每一项的值,求单个点的坐标值需要$O(n)$时间,点值运算需要求$n$个点的坐标值需要$O(n^2)$时间,我们需要别的思路。
奇变偶不变:
接下来,以求
$f(x)=0+x+2x^2+3x^3+4x^4+5x^5+6x^6+7x^7$
这个式子的点值表示法为例
(为了方便后面描述,暂且不将常数项$0$消去)
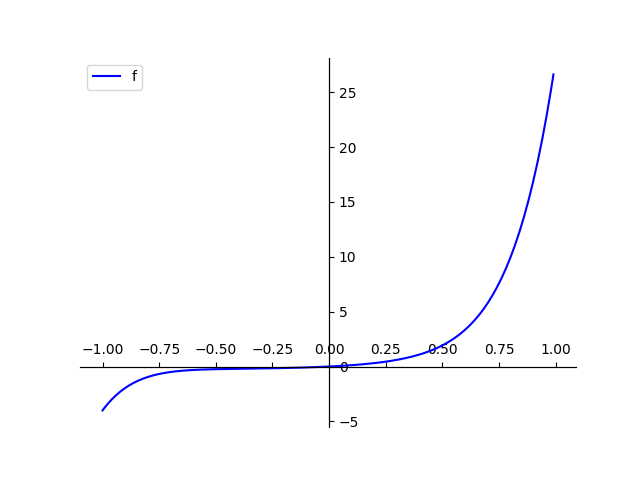
注意,多项式的偶数次项在函数图像上是偶函数,奇数次项在函数图像上是奇函数
那么可以将$f(x)$分成奇函数和偶函数两个部分
$f_{even}(x)=0+2x^2+4x^4+6x^6$
$f_{odd}(x)=x+3x^3+5x^5+7x^7$
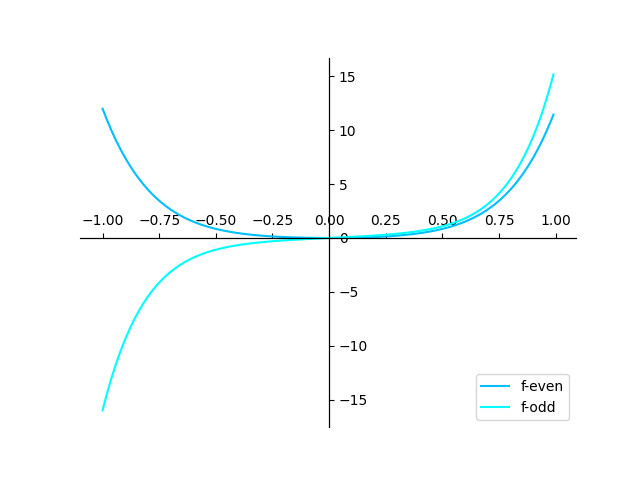
因为
$f_{even}(-x)=f_{even}(x)$
$f_{odd}(x)=-f_{odd}(-x)$
尝试选取这样一组横坐标:
$x=0,-1,1,-2,2,-3,3$
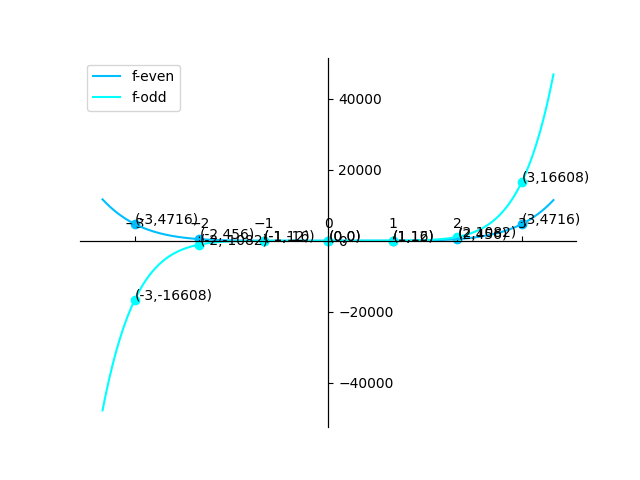
$f_{even}:(-3,4716),(-2,456),(-1,12),(0,0),(1,12),(2,456),(3,4716)$
$f_{odd}:(-3,-16608),(-2,-1082),(-1,-16),(0,0),(1,16),(2,1082),(3,16608)$
这样,需要使用$O(n)$时间进行求值的点只剩下一半,剩下那一半的值相同或是相反数
然后再加回去就得到了$f(x)$在这几个点的值.
$f:(-3,-11892),(-2,-626),(-1,-4),(0,0),(1,28),(2,1538),(3,21324)$
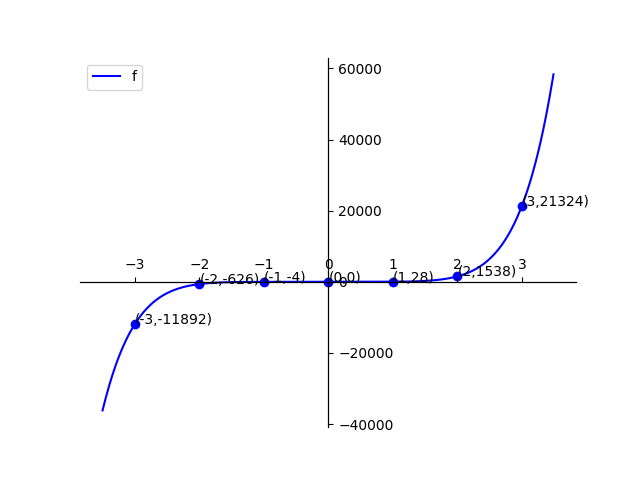
形式化地进行描述,就是假如已经算出$f_{even}(x),f_{odd}(x)$,不仅知道了$f(x)=f_{even}(x),f_{odd}(x)$,还能够立刻得到$f(-x)=f_{even}(x),f_{odd}(-x)$
但这样只是减少了一半的运算量,将时间复杂度仍然是$O(n^2)$
能不能再将需要直接计算的点的数量折半呢?
分治:
将目光拓展一些,不再局限在实数上,回顾复数与复平面的知识.
在复数域上取这样一些点:
$x_0=1$
$x_1=\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i$
$x_2=i$
$x_3=-\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i$
$x_4=-1$
$x_5=-\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}i$
$x_6=-i$
$x_7=\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}i$

注意,
$x_0=x_0^2=x_4^2$
$x_2=x_1^2=x_3^2$
$x_4=x_2^2=x_6^2$
$x_6=x_3^2=x_7^2$
记住这个性质,一会要用到.
视线回到多项式上:
$f(x)=0+x+2x^2+3x^3+4x^4+5x^5+6x^6+7x^7$
在$f_{odd}$中提出一个$x$
$f'_{odd}=\frac{1}{x}f_{odd}=1+3x^2+5x^4+7x^6$
这样$f'_{odd}$也变成了偶函数
这样,知道了$f_{even}(x),f'_{odd}(x)$就能根据$f(x)=f_{even}(x)+xf'_{odd}(x)$算出来了
然后令$(x^{(1)})=x^2$,并进行变量代换,
$f_{even}(x^{(1)})=0+2(x^{(1)})+4(x^{(1)})^2+6(x^{(1)})^3$
$f'_{odd}(x^{(1)})=1+3(x^{(1)})+5(x^{(1)})^2+7(x^{(1)})^3$
还可以分别把$f_{even}(x^{(1)}),f'_{odd}(x^{(1)})$按$y$的指数的奇偶性继续拆分,递归下去
| $f'_{(0,0)}(x^{(0)})=0+x^{(0)}+2(x^{(0)})^{2}+3(x^{(0)})^{3}+4(x^{(0)})^{4}+5(x^{(0)})^{5}+6(x^{(0)})^{6}+7(x^{(0)})^{7}$ | ||||||||
| $f_{(1,0)}(x^{(0)})=0+2(x^{(0)})^{2}+4(x^{(0)})^{4}+6(x^{(0)})^{6}$ $f'_{(1,0)}(x^{(1)})=0+2x^{(1)}+4(x^{(1)})^{2}+6(x^{(1)})^{3}$ |
$f_{(1,4)}(x^{(0)})=x^{(0)}+3(x^{(0)})^{3}+5(x^{(0)})^{5}+7(x^{(0)})^{7}$ $f'_{(1,4)}(x^{(1)})=1+3x^{(1)}+5(x^{(1)})^{2}+7(x^{(1)})^{3}$ |
$x^{(1)}=(x^{(0)})^2$ | ||||||
| $f_{(2,0)}(x^{(1)})=0+4(x^{(1)})^{2}$ $f'_{(2,0)}(x^{(2)})=0+4x^{(2)}$ |
$f_{(2,2)}(x^{(1)})=2x^{(1)}+6(x^{(1)})^{3}$ $f'_{(2,2)}(x^{(2)})=2+6x^{(2)}$ |
$f_{(2,4)}(x^{(1)})=1+5(x^{(1)})^{2}$ $f'_{(2,4)}(x^{(2)})=1+5x^{(2)}$ |
$f_{(2,6)}(x^{(1)})=3x^{(1)}+7(x^{(1)})^{3}$ $f'_{(2,6)}(x^{(2)})=3+7x^{(2)}$ |
$x^{(2)}=(x^{(1)})^2$ | ||||
| $f_{(3,0)}(x^{(2)})=0$ $f'_{(3,0)}(x^{(3)})=0$ |
$f_{(3,1)}(x^{(2)})=4x^{(2)}$ $f'_{(3,1)}(x^{(3)})=4$ |
$f_{(3,2)}(x^{(2)})=2$ $f'_{(3,2)}(x^{(3)})=2$ |
$f_{(3,3)}(x^{(2)})=6x^{(2)}$ $f'_{(3,3)}(x^{(3)})=6$ |
$f_{(3,4)}(x^{(2)})=1$ $f'_{(3,4)}(x^{(3)})=1$ |
$f_{(3,5)}(x^{(2)})=5x^{(2)}$ $f'_{(3,5)}(x^{(3)})=5$ |
$f_{(3,6)}(x^{(2)})=3$ $f'_{(3,6)}(x^{(3)})=3$ |
$f_{(3,7)}(x^{(2)})=7x^{(2)}$ $f'_{(3,7)}(x^{(3)})=7$ |
$x^{(3)}=(x^{(2)})^2$ |
为描述方便,为以上多项式按行数,列数编号
观察将$x^{(0)}=x_4$代入$f'_{(0,0)}(x^{(0)})$,求$f'_{(0,0)}(x_4)$的值的过程.
按照上面的分治方案,只需要求出
$f'_{(1,0)}((x_4)^2)=f'_{(1,0)}(x_0)$
$f'_{(1,4)}((x_4)^2)=f'_{(1,4)}(x_0)$
便能得到
$f'_{(0,0)}(x_4)=f'_{(1,0)}(x_0)+x_4f'_{(1,4)}(x_0)$
再观察将$x^{(0)}=x_0$代入$f'_{(0,0)}(x^{(0)})$,求$f'_{(0,0)}(x_0)$的值的过程.
只需要求出
$f'_{(1,0)}((x_0)^2)=f'_{(1,0)}(x_0)$
$f'_{(1,4)}((x_0)^2)=f'_{(1,4)}(x_0)$
便能得到
$f'_{(0,0)}(x_0)=f'_{(1,0)}(x_0)+x_0f'_{(1,4)}(x_0)$
发现了没,要计算$f'_{(0,0)}(x^{(0)})$在$x^{(0)}=x_4,x_0$两个点的值,只需要计算出$f'_{(1,0)}(x_0),f'_{(1,4)}(x_0)$一组值就行.
这就是
$x_0=x_0^2=x_4^2$
$x_2=x_1^2=x_3^2$
$x_4=x_2^2=x_6^2$
$x_6=x_3^2=x_7^2$
这组性质的意义所在.
同理,要计算$f'_{(0,0)}(x^{(0)})$在$x^{(0)}=x_1,x_3$两个点的值,只需要计算出$f'_{(1,0)}(x_2),f'_{(1,4)}(x_2)$一组值就行.
同理,要计算$f'_{(0,0)}(x^{(0)})$在$x^{(0)}=x_2,x_6$两个点的值,只需要计算出$f'_{(1,0)}(x_2),f'_{(1,4)}(x_4)$一组值就行.
同理,要计算$f'_{(0,0)}(x^{(0)})$在$x^{(0)}=x_3,x_7$两个点的值,只需要计算出$f'_{(1,0)}(x_6),f'_{(1,4)}(x_6)$一组值就行.
$\cdots$
不妨将要求的值以如下的方式存储:
| $f'_{(0,0)}(x_{0})$ | $f'_{(0,0)}(x_{1})$ | $f'_{(0,0)}(x_{2})$ | $f'_{(0,0)}(x_{3})$ | $f'_{(0,0)}(x_{4})$ | $f'_{(0,0)}(x_{5})$ | $f'_{(0,0)}(x_{6})$ | $f'_{(0,0)}(x_{7})$ |
| $f'_{(1,0)}(x_{0})$ | $f'_{(1,0)}(x_{2})$ | $f'_{(1,0)}(x_{4})$ | $f'_{(1,0)}(x_{6})$ | $f'_{(1,4)}(x_{0})$ | $f'_{(1,4)}(x_{2})$ | $f'_{(1,4)}(x_{4})$ | $f'_{(1,4)}(x_{6})$ |
| $f'_{(2,0)}(x_{0})$ | $f'_{(2,0)}(x_{4})$ | $f'_{(2,2)}(x_{0})$ | $f'_{(2,2)}(x_{4})$ | $f'_{(2,4)}(x_{0})$ | $f'_{(2,4)}(x_{4})$ | $f'_{(2,6)}(x_{0})$ | $f'_{(2,6)}(x_{4})$ |
| $f'_{(3,0)}(x_{0})$ | $f'_{(3,1)}(x_{0})$ | $f'_{(3,2)}(x_{0})$ | $f'_{(3,3)}(x_{0})$ | $f'_{(3,4)}(x_{0})$ | $f'_{(3,5)}(x_{0})$ | $f'_{(3,6)}(x_{0})$ | $f'_{(3,7)}(x_{0})$ |
只需要计算出以上这些值,便能得到$f'_{(0,0)}(x^{(0)})$上的八个点的值,实际上的计算复杂度只有$O(n\log n)$,相比$O(n^2)$快多了.
若多项式的次数更高,不妨设次数为$n$($n$必须是$2$的整数次方),只需要取复平面单位元上的$n$均分点即可,实际上就是
$\cos(0)+isin(0)$
$\cos(\frac{2\pi}{n})+i\sin(\frac{2\pi}{n})$
$\cos(2\frac{2\pi}{n})+i\sin(2\frac{2\pi}{n})$
$\cos(3\frac{2\pi}{n})+i\sin(3\frac{2\pi}{n})$
$\cdots$
傅立叶逆变换:
要将点值表示法转换回系数表示法,需要进行一次傅立叶逆变换.
实际上,傅立叶逆变换就是再进行一次傅立叶变换,但对各自变量取其共轭复数(实际上就是自变量的点在复平面上由沿着单位元逆时针转一圈变成了顺时针转一圈),然后对每一位除去一个常数即可,这个常数就是自变量的个数(证明略).
代码:
import math
def FFT(arr,n,logn,inv): #inv为虚部符号,inv为1时FFT,inv为-1时IFFT
if (n == 1): #如果需要转换的只有一项就直接返回
return arr
arr1=arr[0::2]
arr2=arr[1::2]
arr1=FFT(arr1, n//2,logn-1, inv) #递归分治
arr2=FFT(arr2, n//2,logn-1, inv)
w=1
wn=math.cos(2 * math.pi / n)+1j*inv * math.sin(2 * math.pi / n) #单位根
for i in range(n//2):
arr[i] = arr1[i] + w * arr2[i]
arr[i + n // 2] = arr1[i] - w * arr2[i]
w=w*wn
return arr
a=[0,1,2,3,4,5,6,7]
b=[7,6,5,4,3,2,1,0]
l1=max(len(a),len(b))
n=1
logn=0
while(n*2<=l1*2):
n=n*2
logn=logn+1
while(len(a)<n):
a.append(0)
while(len(b)<n):
b.append(0)
a=FFT(a,n,logn,1)
b=FFT(b,n,logn,1)
c=[]
for i in range(len(a)):
c.append(a[i]*b[i])
c=FFT(c,n,logn,-1)
for i in range(len(c)):
c[i]=c[i]/n
for i in range(0,len(c)-1):
print(int(round(c[i].real,0)),end=',')蝴蝶操作:
目光回到这个表格
| $f'_{(0,0)}(x^{(0)})=0+x^{(0)}+2(x^{(0)})^{2}+3(x^{(0)})^{3}+4(x^{(0)})^{4}+5(x^{(0)})^{5}+6(x^{(0)})^{6}+7(x^{(0)})^{7}$ | ||||||||
| $f_{(1,0)}(x^{(0)})=0+2(x^{(0)})^{2}+4(x^{(0)})^{4}+6(x^{(0)})^{6}$ $f'_{(1,0)}(x^{(1)})=0+2x^{(1)}+4(x^{(1)})^{2}+6(x^{(1)})^{3}$ |
$f_{(1,4)}(x^{(0)})=x^{(0)}+3(x^{(0)})^{3}+5(x^{(0)})^{5}+7(x^{(0)})^{7}$ $f'_{(1,4)}(x^{(1)})=1+3x^{(1)}+5(x^{(1)})^{2}+7(x^{(1)})^{3}$ |
$x^{(1)}=(x^{(0)})^2$ | ||||||
| $f_{(2,0)}(x^{(1)})=0+4(x^{(1)})^{2}$ $f'_{(2,0)}(x^{(2)})=0+4x^{(2)}$ |
$f_{(2,2)}(x^{(1)})=2x^{(1)}+6(x^{(1)})^{3}$ $f'_{(2,2)}(x^{(2)})=2+6x^{(2)}$ |
$f_{(2,4)}(x^{(1)})=1+5(x^{(1)})^{2}$ $f'_{(2,4)}(x^{(2)})=1+5x^{(2)}$ |
$f_{(2,6)}(x^{(1)})=3x^{(1)}+7(x^{(1)})^{3}$ $f'_{(2,6)}(x^{(2)})=3+7x^{(2)}$ |
$x^{(2)}=(x^{(1)})^2$ | ||||
| $f_{(3,0)}(x^{(2)})=0$ $f'_{(3,0)}(x^{(3)})=0$ |
$f_{(3,1)}(x^{(2)})=4x^{(2)}$ $f'_{(3,1)}(x^{(3)})=4$ |
$f_{(3,2)}(x^{(2)})=2$ $f'_{(3,2)}(x^{(3)})=2$ |
$f_{(3,3)}(x^{(2)})=6x^{(2)}$ $f'_{(3,3)}(x^{(3)})=6$ |
$f_{(3,4)}(x^{(2)})=1$ $f'_{(3,4)}(x^{(3)})=1$ |
$f_{(3,5)}(x^{(2)})=5x^{(2)}$ $f'_{(3,5)}(x^{(3)})=5$ |
$f_{(3,6)}(x^{(2)})=3$ $f'_{(3,6)}(x^{(3)})=3$ |
$f_{(3,7)}(x^{(2)})=7x^{(2)}$ $f'_{(3,7)}(x^{(3)})=7$ |
$x^{(3)}=(x^{(2)})^2$ |
只观察系数部分:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | 2 | 4 | 6 | 1 | 3 | 5 | 7 |
| 0 | 4 | 2 | 6 | 1 | 5 | 3 | 7 |
| 0 | 4 | 2 | 6 | 1 | 3 | 5 | 7 |
为了计算出最后一行的系数,即
$f'_{(3,0)},f'_{(3,1)},f'_{(3,2)},f'_{(3,3)},f'_{(3,4)},f'_{(3,5)},f'_{(3,6)},f'_{(3,7)}$
前面的方法是分治,每次将偶数次项放在左边,奇数次项放在右边,然后左右两边分别递归,但每次递归都有额外的空间开销,最好找到一种能够帮助原地完成此变换的规律
变换开始与变换结束后数组的状态:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | 4 | 2 | 6 | 1 | 3 | 5 | 7 |
观察它们的二进制表示:
| 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
| 000 | 100 | 010 | 110 | 001 | 101 | 011 | 111 |
规律找到了:某个系数在变换后的位置,是它变换前的位置的二进制表示的反转(证明略)
另:之所以管这个操作叫做蝴蝶操作,是因为有人说这个变换过程长得像蝴蝶
像吗?反正我没觉得.
代码(非递归优化):
import math
def FFT(arr,n,logn,inv):
arr1=[]
for i in range(n): #蝴蝶操作
id1=i
id2=0
for j in range(logn):
id2=id2*2+id1%2
id1=id1//2
arr1.append(arr[id2])
i=1
while(i<n): #待合并的多项式的次数
wn=math.cos(math.pi/i)+ 1j*inv*math.sin(math.pi/i) #将周角平分为2i份的单位根
j=0
while(j<n): #枚举具体区间,j也就是区间右端点
w=1
for k in range(i): #合并
x=arr1[j + k]
y=w* arr1[i + j + k]
#不把xy的值保存下来,会导致后面的计算改变了变量值而出错
arr1[j + k] = x+y
arr1[i + j + k] = x-y
w=w*wn
j=j+i*2
i=i*2
if(inv==-1):
for i in range(n):
arr1[i]=arr1[i]/n
#不要忘了逆变换的时候除掉常数
return arr1
a=[0,1,2,3,4,5,6,7]
b=[7,6,5,4,3,2,1,0]
l1=max(len(a),len(b))
n=1
logn=0
while(n*2<=l1*2):
n=n*2
logn=logn+1
while(len(a)<n):
a.append(0)
while(len(b)<n):
b.append(0)
a=FFT(a,n,logn,1)
b=FFT(b,n,logn,1)
c=[]
for i in range(len(a)):
c.append(a[i]*b[i])
c=FFT(c,n,logn,-1)
for i in range(0,len(c)-1):
print(int(round(c[i].real,0)),end=',')FFT的应用:
参考 Fine-Grained学习笔记(1):卷积,FFT与花式字符串匹配 - Isakovsky - 博客园 (cnblogs.com)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号