二叉树的深度优先遍历和广度优先遍历
二叉树是一种很重要的数据结构,对于二叉树的遍历,有深度优先遍历和广度优先遍历,深度优先遍历又有先序、中序、后续遍历,广度优先遍历就是按层遍历。
1. 深度优先遍历
深度优先遍历,也就是先序、中序、后续遍历,我之前有一篇随笔已经说的很清楚了,在这里我只贴下代码就好了。
传送门:详细教你实现BST(二叉排序树)
在这里我依然用之前建立好的Node、Stack、BST结构来实现代码。
class Node {
constructor(data, leftNode, rightNode) {
this.data = data
this.leftNode = leftNode
this.rightNode = rightNode
}
print () {
return this.data
}
}
class Stack {
constructor() {
this.arr = []
}
pop () {
return this.arr.shift()
}
push (data) {
this.arr.unshift(data)
}
isEmpty () {
return this.arr.length == 0
}
}
class BST {
constructor() {
this.root = null
}
insert (data) {...}
preOrder () {...}
inOrder () {...}
postOrder () {...}
...
}
先是先序、中序、后序遍历的递归实现,很简单。
// 递归先序
function preOrderFn (node) {
if (node) {
console.log(node.print())
preOrderFn(node.leftNode)
preOrderFn(node.rightNode)
}
}
// 递归中序
function inOrderFn (node) {
if (node) {
inOrderFn(node.leftNode)
console.log(node.print())
inOrderFn(node.rightNode)
}
}
// 递归后续
function postOrderFn (node) {
if (node) {
postOrderFn (node.leftNode)
postOrderFn (node.rightNode)
console.log(node.print())
}
}
然后就是先序、中序、后续遍历的非递归实现了。详细的解释和说明,点击上面的传送门就有了,这里不过多赘述。
// 非递归先序
function PreOrderWithoutRecursion (root) {
if (!root)
return
var parentNode = root
var stack = new Stack()
while (parentNode || !stack.isEmpty()) {
// 一直遍历到左子树的最下面,一边打印data,将一路遍历过的节点push进栈中
if (parentNode) {
console.log(parentNode.data)
stack.push(parentNode)
parentNode = parentNode.leftNode
}
// 当parentNode为空时,说明已经达到了左子树的最下面,可以出栈操作了
else {
parentNode = stack.pop()
// 进入右子树,开始新一轮循环
parentNode = parentNode.rightNode
}
}
}
// 非递归中序
function inOrderWithoutRecursion (root) {
if (!root)
return
var parentNode = root
var stack = new Stack()
while (parentNode || !stack.isEmpty()) {
// 一直遍历到左子树的最下面,将一路遍历过的节点push进栈中
if (parentNode) {
stack.push(parentNode)
parentNode = parentNode.leftNode
}
// 当parentNode为空时,说明已经达到了左子树的最下面,可以出栈操作了
else {
parentNode = stack.pop()
console.log(parentNode.data)
// 进入右子树,开始新一轮循环
parentNode = parentNode.rightNode
}
}
}
// 非递归后续
function PostOrderWithoutRecursion (root) {
if (!root)
return
var parentNode = root
var stack = new Stack()
var lastVisitNode = null
while (parentNode || !stack.isEmpty()) {
if (parentNode) {
stack.push(parentNode)
parentNode = parentNode.leftNode
}
else {
parentNode = stack.pop()
// 如果当前节点没有右节点或者是右节点被访问过,则访问当前节点
if (!parentNode.rightNode || parentNode.rightNode.data == lastVisitNode.data) {
console.log(parentNode.data)
lastVisitNode = parentNode
}
// 访问右节点
else {
stack.push(parentNode)
parentNode = parentNode.rightNode
while (parentNode) {
parentNode = parentNode.leftNode
}
}
}
}
}
2. 广度优先遍历
其实这片随笔有点打酱油了,只说了两个遍历,还有一个是在以前实现过的。
广度优先遍历,顾名思义,就是横向先遍历,也就是按层次遍历,从根节点往下,对每一层依此访问,在每一层中从左到右(也可以从右到左)遍历,遍历完一层就进入下一层,直到没有节点。
之前讲深度优先非递归遍历的时候,我们用到了一个栈的数据结构,到了广度优先遍历的时候,我们就要用到队列这个数据结构。
为什么上一次用栈,这一次就要用到队列了呢?
拿非递归中序遍历举例,我们每遍历到一个节点就要进行入栈操作,遍历完左节点之后,还需要找到根节点,再通过根节点找到右节点,所以我们需要最后遍历到的节点在这个数据结构的最顶端,这不就是栈吗?
先把我们的队列的数据结构先建立起来再说。依然用数组模拟队列的操作。
class Queue {
constructor () {
this.arr = []
}
enqueue (data) {
return this.arr.push(data)
}
dequeue () {
return this.arr.shift()
}
isEmpty () {
return this.arr.length == 0
}
}
为什么要用队列呢,我们按层次遍历,首先遍历根节点,然后左子树,右子树,然后左子树的左子树,左子树的右子树,右子树的左子树,依此类推。每遍历到一个节点,就将它存在一个数据结构里,先把它的前面的节点遍历完,才能遍历它,也就是一个先进先出(FIFO)的遍历方式,这不就是队列吗?
说下思路:首先现将根节点做入队操作,队列里的节点表示我们要遍历的节点,所以队列为空的时候也就是没有节点可以遍历了,即队列不为空的时候循环遍历整个队列。首先我们取出队列的第一个节点,也就是对这个队列做出队操作,访问这个节点的值,如果这个节点存在左子树,那么将它的左子树放在队列的末尾,也就是对左子树做入队操作,右子树同理。
思路很简单,实现起来不难:
class BST {
constructor() {
this.root = null
}
// 广度优先遍历
levelOrderTraversal () {
levelOrderTraversalFn(this.root)
}
insert (data) {...}
preOrder () {...}
inOrder () {...}
postOrder () {...}
find (data) {..}
getMax () {...}
getMin () {...}
deleteNode (data) {...}
depth () {...}
nodeCount () {...}
}
// 广度优先遍历
function levelOrderTraversalFn (node) {
if(!node) {
return
}
var que = new Queue()
que.enqueue(node)
while(!que.isEmpty()) {
node = que.dequeue()
console.log(node.data)
if(node.leftNode) que.enqueue(node.leftNode)
if(node.rightNode) que.enqueue(node.rightNode)
}
}
我们试一下:
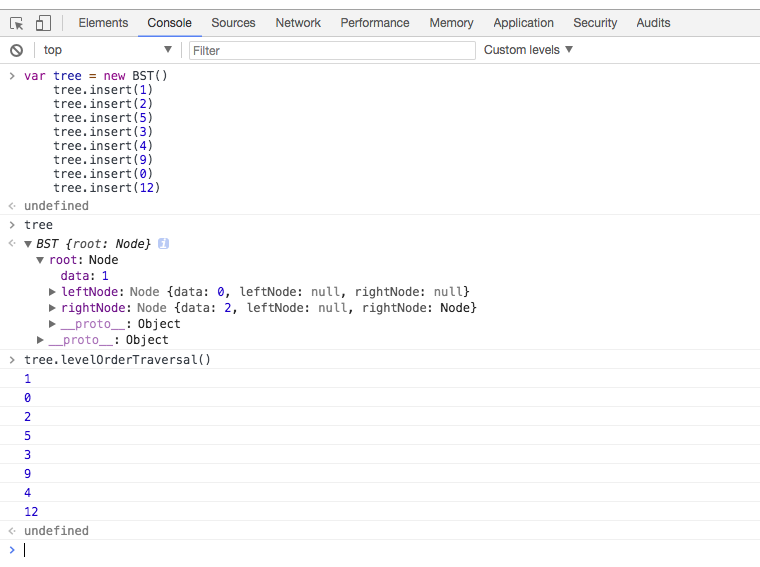
没错,那我们的广度优先遍历也就写完了。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号