算法模型指标评估验证合集
这个图表展示了二分类问题中常用的各种评价指标及其计算公式。以下是对每个指标的详细分析和总结:
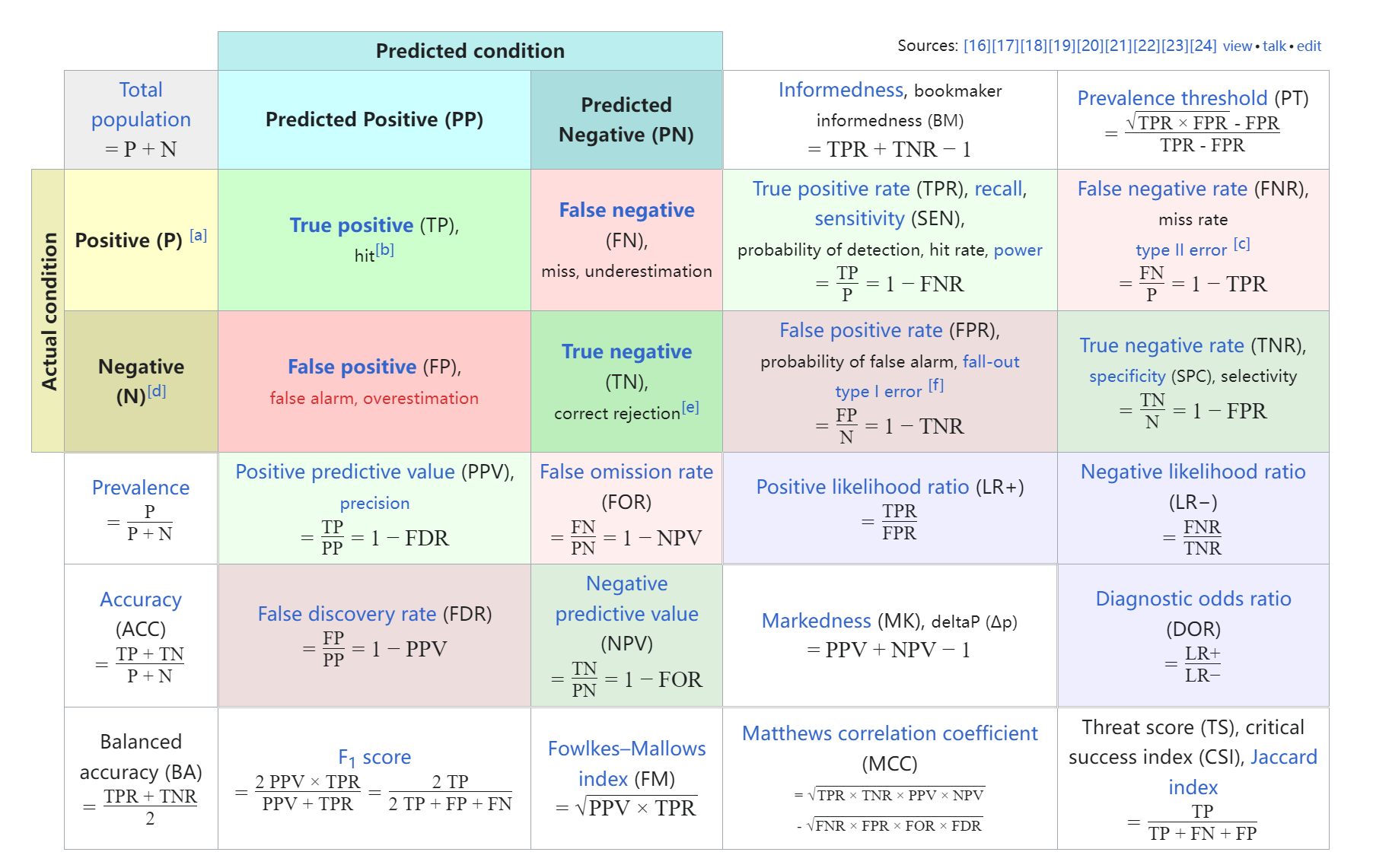
图表结构分析
-
总样本数 (Total population):
- ( P + N ):总样本数,包括正类样本和负类样本。
-
实际情况 (Actual Condition):
- 正类 (Positive, P):实际为正类的样本数。
- 负类 (Negative, N):实际为负类的样本数。
-
预测情况 (Predicted Condition):
- 预测为正类 (Predicted Positive, PP):被预测为正类的样本数。
- 预测为负类 (Predicted Negative, PN):被预测为负类的样本数。
-
混淆矩阵 (Confusion Matrix):
- 真正类 (True Positive, TP):实际为正类且被正确预测为正类的样本数。
- 假负类 (False Negative, FN):实际为正类但被错误预测为负类的样本数。
- 假正类 (False Positive, FP):实际为负类但被错误预测为正类的样本数。
- 真负类 (True Negative, TN):实际为负类且被正确预测为负类的样本数。
各指标的含义及意义
-
准确率 (Accuracy, ACC):
- 公式:( \(\text{ACC} = \frac{TP + TN}{P + N}\) )
- 含义:预测正确的样本数占总样本数的比例。
- 意义:衡量模型整体的预测准确性。
-
精确率 (Precision, PPV):
- 公式:( $\text{PPV} = \frac{TP}{TP + FP} $)
- 含义:预测为正类的样本中实际为正类的比例。
- 意义:衡量模型在预测正类时的准确性。
-
召回率 (Recall, TPR):
- 公式:( \(\text{TPR} = \frac{TP}{P}\) )
- 含义:实际为正类的样本中被正确预测为正类的比例。
- 意义:衡量模型对正类样本的识别能力。
-
特异性 (Specificity, TNR):
- 公式:( \(\text{TNR} = \frac{TN}{N}\) )
- 含义:实际为负类的样本中被正确预测为负类的比例。
- 意义:衡量模型对负类样本的识别能力。
-
假正率 (False Positive Rate, FPR):
- 公式:( \text{FPR} = \frac{FP}{N} )
- 含义:实际为负类的样本中被错误预测为正类的比例。
- 意义:衡量模型在负类样本中的误报率。
-
假负率 (False Negative Rate, FNR):
- 公式:( \(\text{FNR} = \frac{FN}{P}\) )
- 含义:实际为正类的样本中被错误预测为负类的比例。
- 意义:衡量模型在正类样本中的漏报率。
-
F1分数 (F1 Score):
- 公式:( \(\text{F1} = \frac{2 \cdot \text{PPV} \cdot \text{TPR}}{\text{PPV} + \text{TPR}}\) )
- 含义:精确率和召回率的调和平均数。
- 意义:综合衡量模型的精确率和召回率。
-
平衡准确率 (Balanced Accuracy, BA):
- 公式:( \(\text{BA} = \frac{TPR + TNR}{2}\) )
- 含义:召回率和特异性的平均值。
- 意义:在类别不平衡的情况下,衡量模型的整体表现。
-
Matthews相关系数 (Matthews Correlation Coefficient, MCC):
- 公式:( \(\text{MCC} = \frac{TP \cdot TN - FP \cdot FN}{\sqrt{(TP + FP)(TP + FN)(TN + FP)(TN + FN)}}\) )
- 含义:考虑了TP、TN、FP和FN的综合指标。
- 意义:在类别不平衡的情况下,衡量模型的分类性能。
-
诊断比值比 (Diagnostic Odds Ratio, DOR):
-
公式:( \(\text{DOR} = \frac{TP \cdot TN}{FP \cdot FN}\) )
-
含义:真正类和假正类的比值与假负类和真负类的比值之比。
-
意义:衡量模型区分正类和负类的能力。
-
-
假发现率 (False Discovery Rate, FDR):
- 公式:FDR=𝐹𝑃𝑇𝑃+𝐹𝑃FDR=TP+FP**FP
- 含义:预测为正类的样本中实际为负类的比例。
- 意义:衡量模型在预测正类时的误报率。
- 负预测值 (Negative Predictive Value, NPV):
- 公式:NPV=𝑇𝑁𝑇𝑁+𝐹𝑁NPV=TN+FN**TN
- 含义:预测为负类的样本中实际为负类的比例。
- 意义:衡量模型在预测负类时的准确性。
- 假遗漏率 (False Omission Rate, FOR):
- 公式:FOR=𝐹𝑁𝑇𝑁+𝐹𝑁FOR=TN+FN**FN
- 含义:预测为负类的样本中实际为正类的比例。
- 意义:衡量模型在预测负类时的漏报率。
- 正似然比 (Positive Likelihood Ratio, PLR):
- 公式:PLR=𝑇𝑃𝑅𝐹𝑃𝑅PLR=FPR**TPR
- 含义:真正类率与假正类率的比值。
- 意义:衡量模型预测正类的可信度。
- 负似然比 (Negative Likelihood Ratio, NLR):
- 公式:NLR=𝐹𝑁𝑅𝑇𝑁𝑅NLR=TNR**FNR
- 含义:假负类率与真负类率的比值。
- 意义:衡量模型预测负类的可信度。
- 诊断准确性 (Diagnostic Accuracy, DA):
- 公式:DA=𝑇𝑃+𝑇𝑁𝑃+𝑁DA=P+N**TP+TN
- 含义:预测正确的样本数占总样本数的比例。
- 意义:衡量模型整体的预测准确性。
- 信息量 (Informedness, BM):
- 公式:BM=𝑇𝑃𝑅+𝑇𝑁𝑅−1BM=TPR+TNR−1
- 含义:真正类率和真负类率之和减去1。
- 意义:衡量模型在识别正类和负类样本时的信息量。
- 标记度 (Markedness, MK):
- 公式:MK=𝑃𝑃𝑉+𝑁𝑃𝑉−1MK=PP**V+NP**V−1
- 含义:正预测值和负预测值之和减去1。
- 意义:衡量模型在预测正类和负类样本时的标记度。
- Fowlkes-Mallows指数 (Fowlkes-Mallows Index, FMI):
- 公式:FMI=PPV⋅TPRFMI=PPV⋅TPR
- 含义:精确率和召回率的几何平均数。
- 意义:综合衡量模型的精确率和召回率。
-
Matthews相关系数 (Matthews Correlation Coefficient, MCC):
- 公式:MCC=𝑇𝑃⋅𝑇𝑁−𝐹𝑃⋅𝐹𝑁(𝑇𝑃+𝐹𝑃)(𝑇𝑃+𝐹𝑁)(𝑇𝑁+𝐹𝑃)(𝑇𝑁+𝐹𝑁)MCC=(TP+FP)(TP+FN)(TN+FP)(TN+FN)TP⋅TN−FP⋅FN
- 含义:考虑了TP、TN、FP和FN的综合指标。
- 意义:在类别不平衡的情况下,衡量模型的分类性能。
-
威胁评分 (Threat Score, TS):
- 公式:TS=𝑇𝑃𝑇𝑃+𝐹𝑁+𝐹𝑃TS=TP+FN+FP**TP
- 含义:真正类数与真正类、假负类和假正类之和的比值。
- 意义:衡量模型在预测正类时的综合性能。
-
假发现率 (False Discovery Rate, FDR):
- 公式:FDR=𝐹𝑃𝑇𝑃+𝐹𝑃FDR=TP+FP**FP
- 含义:预测为正类的样本中实际为负类的比例。
- 意义:衡量模型在预测正类时的误报率。
- 流行率 (Prevalence):
- 公式:Prevalence=𝑃𝑃+𝑁Prevalence=P+N**P
- 含义:正类样本在总样本中的比例。
- 意义:衡量数据集中正类样本的比例,反映了问题的实际情况。
- 流行率阈值 (Prevalence Threshold, PT):
- 公式:PT=FPR/(TPR+FPR)PT=FPR/(TPR+FPR)
- 含义:在给定的流行率下,达到最佳分类性能的阈值。
- 意义:帮助确定在特定流行率下的最佳决策阈值。
- 诊断比值比 (Diagnostic Odds Ratio, DOR):
- 公式:DOR=𝑇𝑃⋅𝑇𝑁𝐹𝑃⋅𝐹𝑁DOR=FP⋅FN**TP⋅TN
- 含义:真正类和假正类的比值与假负类和真负类的比值之比。
- 意义:衡量模型区分正类和负类的能力。
- 威胁评分 (Threat Score, TS):
- 公式:TS=𝑇𝑃𝑇𝑃+𝐹𝑁+𝐹𝑃TS=TP+FN+FP**TP
- 含义:真正类数与真正类、假负类和假正类之和的比值。
- 意义:衡量模型在预测正类时的综合性能。
- Matthews相关系数 (Matthews Correlation Coefficient, MCC):
- 公式:MCC=𝑇𝑃⋅𝑇𝑁−𝐹𝑃⋅𝐹𝑁(𝑇𝑃+𝐹𝑃)(𝑇𝑃+𝐹𝑁)(𝑇𝑁+𝐹𝑃)(𝑇𝑁+𝐹𝑁)MCC=(TP+FP)(TP+FN)(TN+FP)(TN+FN)TP⋅TN−FP⋅FN
- 含义:考虑了TP、TN、FP和FN的综合指标。
- 意义:在类别不平衡的情况下,衡量模型的分类性能。
- Fowlkes-Mallows指数 (Fowlkes-Mallows Index, FMI):
- 公式:FMI=PPV⋅TPRFMI=PPV⋅TPR
- 含义:精确率和召回率的几何平均数。
- 意义:综合衡量模型的精确率和召回率。
- 标记度 (Markedness, MK):
- 公式:MK=𝑃𝑃𝑉+𝑁𝑃𝑉−1MK=PP**V+NP**V−1
- 含义:正预测值和负预测值之和减去1。
- 意义:衡量模型在预测正类和负类样本时的标记度。
- 信息量 (Informedness, BM):
- 公式:BM=𝑇𝑃𝑅+𝑇𝑁𝑅−1BM=TPR+TNR−1
- 含义:真正类率和真负类率之和减去1。
- 意义:衡量模型在识别正类和负类样本时的信息量。
结论
这个图表详细展示了二分类问题中常用的各种评价指标及其计算公式。每个指标都有其特定的含义和意义,用于衡量模型在不同方面的性能:
- 准确率和精确率:衡量模型整体的预测准确性和在预测正类时的准确性。
- 召回率和特异性:衡量模型对正类和负类样本的识别能力。
- 假正率和假负率:衡量模型在负类和正类样本中的误报率和漏报率。
- F1分数:综合衡量模型的精确率和召回率。
- 平衡准确率和Matthews相关系数:在类别不平衡的情况下,衡量模型的整体表现。
- 诊断比值比:衡量模型区分正类和负类的能力。
- 假发现率和负预测值:衡量模型在预测正类和负类时的误报率和准确性。
- 假遗漏率:衡量模型在预测负类时的漏报率。
- 正似然比和负似然比:衡量模型预测正类和负类的可信度。
- 诊断准确性:衡量模型整体的预测准确性。
- 信息量和标记度:衡量模型在识别正类和负类样本时的信息量和标记度。
- Fowlkes-Mallows指数:综合衡量模型的精确率和召回率。
- Matthews相关系数:在类别不平衡的情况下,衡量模型的分类性能。
- 威胁评分:衡量模型在预测正类时的综合性能。
- 流行率:衡量数据集中正类样本的比例,反映了问题的实际情况。
- 流行率阈值:帮助确定在特定流行率下的最佳决策阈值。
- 诊断比值比:衡量模型区分正类和负类的能力。
- 威胁评分:衡量模型在预测正类时的综合性能。
- Matthews相关系数:在类别不平衡的情况下,衡量模型的分类性能。
- Fowlkes-Mallows指数:综合衡量模型的精确率和召回率。
- 标记度:衡量模型在预测正类和负类样本时的标记度。
- 信息量:衡量模型在识别正类和负类样本时的信息量。
这些指标可以帮助我们全面评估模型的性能,选择最适合特定应用场景的模型。
通过综合使用这些指标,我们可以更好地理解模型的优缺点,从而进行更有效的模型优化和改进。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号