《人工智能：线代方法》 第二部分问题求解 通过搜索进行问题求解(4) 启发式函数

、# 《人工智能：线代方法》 第二部分问题求解 通过搜索进行问题求解(4)

3.6 启发式函数

启发式函数h(n)告诉A*从任意结点n到目标结点的最小代价评估值。选择一个好的启发式函数是重要的。

3.6.1 启发式函数的准确性对性能的影响

启发式函数可以控制A*的行为：

一种极端情况，如果\(h(n)\)是0，则只有\(g(n)\)起作用，此时A演变成Dijkstra算法，这保证能找到最短路径。
如果\(h(n)\)经常都比从n移动到目标的实际代价小（或者相等），则A保证能找到一条最短路径。\(h(n)\)越小，A扩展的结点越多，运行就得越慢。
如果\(h(n)\)精确地等于从n移动到目标的代价，则A将会仅仅寻找最佳路径而不扩展别的任何结点，这会运行得非常快。尽管这不可能在所有情况下发生，你仍可以在一些特殊情况下让它们精确地相等（译者：指让h(n)精确地等于实际值）。只要提供完美的信息，A会运行得很完美，认识这一点很好。
如果\(h(n)\)有时比从n移动到目标的实际代价高，则A不能保证找到一条最短路径，但它运行得更快。
另一种极端情况，如果\(h(n)\)比\(g(n)\)大很多，则只有\(h(n)\)起作用，A演变成BFS算法。
　　所以我们得到一个很有趣的情况，那就是我们可以决定我们想要从A中获得什么。理想情况下（注：原文为At exactly the right point），我们想最快地得到最短路径。如果我们的目标太低，我们仍会得到最短路径，不过速度变慢了；如果我们的目标太高，那我们就放弃了最短路径，但A*运行得更快。

在游戏中，A*的这个特性非常有用。例如，你会发现在某些情况下，你希望得到一条好的路径（"good" path）而不是一条完美的路径（"perfect" path）。为了权衡\(g(n)\)和\(h(n)\)，你可以修改任意一个。

注:在学术上，如果启发式函数值是对实际代价的低估，A算法被称为简单的A算法（原文为simply A）。然而，我继续称之为A，因为在实现上是一样的，并且在游戏编程领域并不区别A和A*。

　　启发式函数h(n)告诉A*从任意结点n到目标结点的最小代价评估值。选择一个好的启发式函数是重要的。

(1) 速度还是精确度？

　　A*改变它自己行为的能力基于启发式代价函数，启发式函数在游戏中非常有用。在速度和精确度之间取得折衷将会让你的游戏运行得更快。在很多游戏中，你并不真正需要得到最好的路径，仅需要近似的就足够了。而你需要什么则取决于游戏中发生着什么，或者运行游戏的机器有多快。

​ 假设你的游戏有两种地形，平原和山地，在平原中的移动代价是1而在山地则是3。A* is going to search three times as far along flat land as it does along mountainous land. 这是因为有可能有一条沿着平原到山地的路径。把两个邻接点之间的评估距离设为1.5可以加速A的搜索过程。然后A会将3和1.5比较，这并不比把3和1比较差。

​ 速度和精确度之间的选择前不是静态的。你可以基于CPU的速度、用于路径搜索的时间片数、地图上物体（units）的数量、物体的重要性、组（group）的大小、难度或者其他任何因素来进行动态的选择。取得动态的折衷的一个方法是，建立一个启发式函数用于假定通过一个网格空间的最小代价是1，然后建立一个代价函数（cost function）用于测量（scales）：

\[g’(n) = 1 + alpha * ( g(n) – 1 ) \]

　　如果alpha是0，则改进后的代价函数的值总是1。这种情况下，地形代价被完全忽略，A工作变成简单地判断一个网格可否通过。如果alpha是1，则最初的代价函数将起作用，然后你得到了A的所有优点。你可以设置alpha的值为0到1的任意值。

　　你也可以考虑对启发式函数的返回值做选择：绝对最小代价或者期望最小代价。例如，如果你的地图大部分地形是代价为2的草地，其它一些地方是代价为1的道路，那么你可以考虑让启发式函数不考虑道路，而只返回2*距离。

　　速度和精确度之间的选择并不是全局的。
　　在地图上的某些区域，精确度是重要的，你可以基于此进行动态选择。例如，假设我们可能在某点停止重新计算路径或者改变方向，则在接近当前位置的地方，选择一条好的路径则是更重要的，因此为何要对后续路径的精确度感到厌烦？或者，对于在地图上的一个安全区域，最短路径也许并不十分重要，但是当从一个敌人的村庄逃跑时，安全和速度是最重要的。（译者注：译者认为这里指的是，在安全区域，可以考虑不寻找精确的最短路径而取近似路径，因此寻路快；但在危险区域，逃跑的安全性和逃跑速度是重要的，即路径的精确度是重要的，因此可以多花点时间用于寻找精确路径。）

(2) 衡量单位

　A计算f(n) = g(n) + h(n)。为了对这两个值进行相加，这两个值必须使用相同的衡量单位。如果g(n)用小时来衡量而h(n)用米来衡量，那么A将会认为g或者h太大或者太小，因而你将不能得到正确的路径，同时你的A*算法将运行得更慢。

(3) 精确的启发式函数

　　如果你的启发式函数精确地等于实际最佳路径（optimal path），如下一部分的图中所示，你会看到此时A扩展的结点将非常少。A算法内部发生的事情是：在每一结点它都计算f(n) = g(n) + h(n)。当h(n)精确地和g(n)匹配（译者注：原文为match）时，f(n)的值在沿着该路径时将不会改变。不在正确路径（right path）上的所有结点的f值均大于正确路径上的f值（译者注：正确路径在这里应该是指最短路径）。如果已经有较低f值的结点，A*将不考虑f值较高的结点，因此它肯定不会偏离最短路径。

(4) 预计算的精确启发式函数

　　构造精确启发函数的一种方法是预先计算任意一对结点之间最短路径的长度。在许多游戏的地图中这并不可行。然后，有几种方法可以近似模拟这种启发函数：

​ Fit a coarse grid on top of the fine grid. Precompute the shortest path between any pair of coarse grid locations.
Precompute the shortest path between any pair of waypoints. This is a generalization of the coarse grid approach.
（译者：此处不好翻译，暂时保留原文）

然后添加一个启发函数h’用于评估从任意位置到达邻近导航点（waypoints）的代价。（如果愿意，后者也可以通过预计算得到。）最终的启发式函数可以是：

\[h(n) = h'(n, w1) + distance(w1, w2), h'(w2, goal) \]

或者如果你希望一个更好但是更昂贵的启发式函数，则分别用靠近结点和目标的所有的w1,w2对对上式进行求值。（译者注：原文为or if you want a better but more expensive heuristic, evaluate the above with all pairs w1, w2 that are close to the node and the goal, respectively.）

(5) 线性精确启发式算法

　　在特殊情况下，你可以不通过预计算而让启发式函数很精确。如果你有一个不存在障碍物和slow地形，那么从初始点到目标的最短路径应该是一条直线。

　　如果你正使用简单的启发式函数（我们不知道地图上的障碍物），则它应该和精确的启发式函数相符合。如果不是这样，则你会遇到衡量单位的问题，或者你所选择的启发函数类型的问题。

• 一种描述启发式函数质量的方法是有效分支因子(effective branching factor)b* 。如果针对一个特定问题，A* 搜索所生成的总节点数是n，而解的深度是\(d\)，那么\(b^*\)就是深度为\(d\)的均衡树要包含\(n + 1\)个节点所必需的分支因子。因此有：

  \[n + 1 = 1 + b^{*} + (b^{*})^2 + \dots + (b^{*})^d \]

  在不同的问题实例中，有效分支因子可能会发生变化，但通常对于特定领域，在所有复杂的问题实例中它都是相当恒定的。
  因此，对一小部分问题的\(b^{*}\)进行实验测量可以为启发式函数的总体有用性提供良好的指导。设计良好的启发式函数的\(b^{*}\)接近1，使得我们能以合理的计算代价求解相当大的问题。

• 对于一个使用给定启发式函数\(h\)的\(A^{*}\)剪枝刻画其效果的一个更好方式是：有效深度(effective depth)相比于真实深度的减少量\(k_{h}\)(一个常数)。这意味着相较于无信息搜索的代价\(O(b^{d})\)，上述方式的总搜索代价为\(O(b^{d - k_{n}})\)。

• 通常情况下，主要启发式函数是一致的，并且其计算时间不太长，使用具有较高值的启发式函数效果都会更好。

3.6.2 从松弛问题出发生成启发式函数

• 减少了对动作的限制条件的问题称为松弛问题(relaxed problem)。

• 松弛问题的状态空间图是原始状态空间的一个超图，因为删除限制条件会导致条件会导致原图中边的增加。

• 因为松弛问题向状态空间图中添加了一些边，根据定义，原问题的任一最优解也是松弛问题的一个解；但是，如果增加的边提供了捷径，松弛问题可能有更好的解。
  因此，松弛问题中最优解的代价可以作为原问题的一个可容许的启发式函数。
  此外，因为得到的启发式函数是松弛问题的准确代价，所以它一定满足三角不等式，因此它是一致的。

• \(A_{BSOLVER}\)程序可以通过“松弛问题”方法及各种其他技术从问题定义中自动生成启发式函数(Prieditis，1993)。\(A_{BSOLVER}\)为8数码问题生成了一种新的启发式函数，它优于任何已有的启发式函数。

• 如果一个可容许的启发式函数集合\(h_1,\dots, h_m\)可以求解同一个问题，但没有一个函数明显优于其他函数，那么我们应该选择哪个函数?事实证明，我们可以通过如下定义，得到最优的启发式函数：

  \[h(n) = max \left\{ h_1(n), \dots, h_{k}(n) \right\} \]

  这种复合启发式函数将选择对于所讨论节点最准确的函数。
  因为\(h_{i}\)都是容许的，所以\(h\)也是可容许的(如果\(h_i\)都是一致的，则\(h\)也是一致的)。此外，\(h\)优于所有组成它的启发式函数。
  唯一的缺点是\(h(n)\)的计算时间更长。如果考虑这一问题，另一种选择是在每次评价时随机选择一个启发式函数，或者使用机器学习算法来预测哪个启发式函数是最优的。这样做可能会导致启发式函数失去一致性(即使每个\(h_i\)都是一致的)，但在实践中，它通常能更快地求解问题。

3.6.3 从子问题出发生成启发式函数:模式数据库

• 从容许的启发式函数，也可以由给定问题的子问题(subproblem)的解代价推到得到。
• 子问题最优解的代价是完整问题代价的一个下界。在某些情况下，它比曼哈顿距离更准确。
• 那么这两个代价的和仍然是求解完整问题代价的一个下界。
  这就是不相交模式数据库（disjoint pattern database）的思想。
• 有了这样的数据库，可以在几毫秒内求解随机的 15 数码问题——与使用曼哈顿距离相比，生成的节点数不到原来的万分之一。

3.6.4 使用地标生成启发式函数

• 这里有很多技巧，但最重要的是对一些最优路径代价的预计算（precomputation）。虽然预计算可能相当耗时，但只需完成一次预计算，就可以摊销数十亿用户的搜索请求。

• 更好的方法是从顶点中选择一些（也许 10 个或 20 个）地标点（landmark point）。

• 然后，对于图中每个地标 L 和每个其他顶点 v，我们计算并存储\(C^*(v,L)\)，即从\(v\)到\(L\)的最优路径的准确代价。（我们同样需要\(C^*(L, v)\)；

  • 在无向图上，\(C^*(L, v)\) 与\(C^*(v, L)\)相同；
    在有向图上，如单行道，我们则需要单独计算\(C^* (L, v)\)。给定存储的\(C^*\)表，我们可以很容易地创建出一个高效的（尽管是不可容许的）启发式函数：
    在所有地标中，从当前节点到地标然后到目标节点代价的最小值为

    \[h_L(n) = \min_{L \in Landmark}C^{*}(n,L) + C^{*}{L, goal} \]
    • 如果最优路径刚好经过一个地标，这个启发式函数将是准确的；
    • 否则，这个启发式函数就是不可容许的——它高估了到目标的代价。
      在 A* 搜索中，如果启发式函数是准确的，那么一旦到达一个位于最优路径上的节点，此后所扩展的每个节点都将位于最优路径上。把等值线想象为沿着这条最优路径前进。搜索将沿着最优路径进行，在每次迭代中加入一个代价为 c 的动作，然后到达一个 h 值减少 c 的结果状态，这意味着在整条路径上总的 f = g + h 得分将保持在常量 C*。

  • 一些寻径算法通过在图中添加捷径（shortcut）——人工定义的对应于一条最优多行动路径的边——来节省更多的时间。

  • \(h_L(n)\) 是高效的，但不是可容许的。只要稍加注意，我们就可以提出一种既高效又可容许
    的启发式函数：

    \[h_{DH}(n) = \max_{L \in Landmark} |C^*(n,L) - C^*(goal, L| \]

    这被称为差分启发式（differential heuristic）函数（因为包含减法）。可以把它理解为在比目标
    还要远的某个位置设置一个地标点。如果目标恰好在从 n 到该地标点的最优路径上，那么“考虑从 n 到 L 的完整路径，然后减去这条路径的最后一部分，即从 goal 到 L，即可得到从 n 到goal 的这段路径的准确代价”。如果目标稍微偏离到地标的最优路径，启发式函数将是不准确的，但仍然是可容许的。比目标近的地标是没有用的；例如，一个恰好位于 n 和 goal 正中间的地标将导致 hDH = 0，这是没有用的。

  • 几种选择地标点的方法。

    • 随机选择
      ——随机选择速度较快，但如果我们多花些功夫将地标
      分散开来，使得它们彼此之间不太接近，我们将得到更好的结果。
    • 贪心方法
      ——贪心方法是随机选择第一个
      地标，然后找到离它最远的点，将其添加到地标集合中，接着在每次迭代中添加离最近地标
      最远的点。
    • 最近搜索方法
      ——如果你有用户过去的搜索请求日志，那么你可以选择搜索中经常请求的地点作为
      地标。
    • 差分启发式函数
      ——对于差分启发式函数，地标分布在图的周界上更好。因此，一个比较好的技术是找到图的质心，围绕质心划分出 k 个楔形（就像饼状图一样），并在每个楔形中选择离中心最远的顶点。

    地标在寻径问题上尤其有效，这是由世界上道路的布局方式导致的：许多交通运输实际上都是在地标之间穿行，所以土木工程师在这些路线上修建最宽、最快的道路；地标式搜索可以更轻松地复原这些路线。

3.6.5 学习以更好地搜索

几种固定的搜索策略(广度优先，A* 等)，这些都是计算机科学家精心设计和编程实现的。
那么智能体能自己学习如何更好地搜索吗？答案是坑爹的，这种方法基于一个重要的概念，元级状态空间(metalevel state space)。

元级状态空间中的每个状态将捕捉在普通状态空间（例如罗马尼亚地图）进行搜索的程序的内部（计算）状态。
［为了区分这两个概念，我们将罗马尼亚地图称为对象级状态空间（object-level state space）。］
例如，A* 算法的内部状态当前搜索树组成。元级状态空间中的每个动作都是一个改变内部状态的计算步；
例如，A* 中的每一个计算步扩展一个叶节点，并将其后续节点添加到树中。

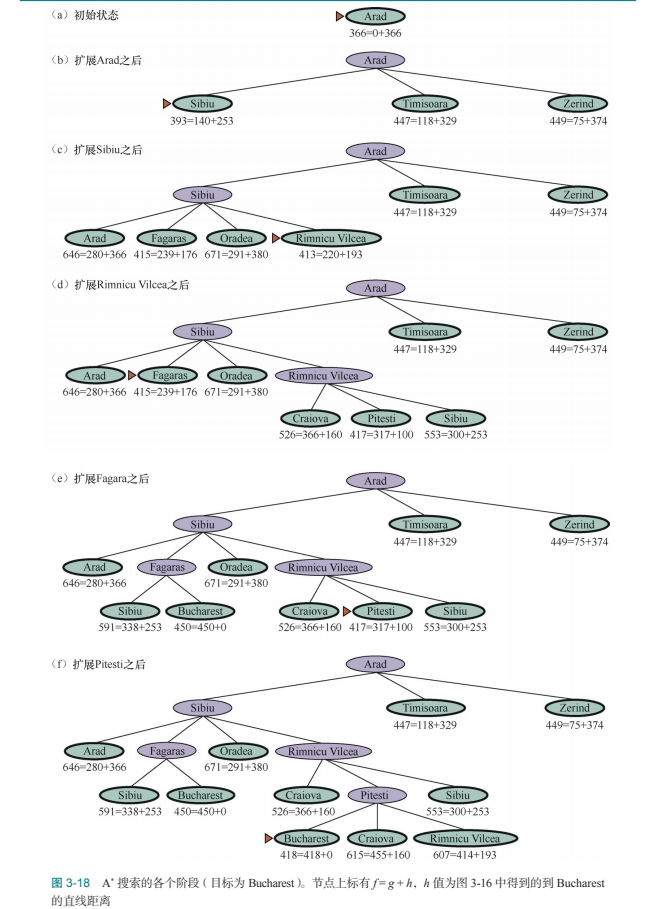
因此，图 3-18 展示了一个逐渐增大的搜
索树序列，它描述了元级状态空间中的一条路径，路径上的每个状态都是一棵对象级搜索树。

现在，图 3-18 中的路径共有 5 步，包括一个扩展 Fagaras 的步骤，这一步不是非常有用。

对于更困难的问题，将存在很多这样的错误步骤，元级学习（metalevel learning）算法可以从这些经验中学习，以避免探索毫无希望的子树。学习的目标是对计算开销和路径代价进行权衡，以最小化求解问题的总代价。

3.6.6 从经验中学习启发式函数

​ 我们已经看到，生成启发式函数的一种方法是设计一个容易找到最优解的松弛问题，另一种选择是从经验中学习。这里的“经验”意味着，例如，求解大量 8 数码问题。

• 一个 8 数码问题的每个最优解都提供了一个“(目标, 路径)”对作为示例。可以利用学习算法通过这些示例构造一个函数 h，（幸运的话）它可以近似搜索过程中出现的其他状态的真实路径代价。这些方法中的大多数学习到的都是启发式函数的一个不完美的近似，因此存在启发式函数不可容许的风险。这必然导致算法需要在学习时间、搜索运行时间和解的代价之间进行权衡。
  如果除了原始状态描述外，还提供与预测启发式函数值相关的状态特征（feature），那么一些机器学习技术将表现得更好。例如，“错位滑块数”这一特征可能有助于预测 8 数码问题
  中状态与目标的实际距离。我们将这一特征记作\(x_1(n)\)。

• 我们可以使用 100 个随机生成的 8 数码配置，并收集其真实解代价的统计数据。我们可能会发现，当\(x_1(n) = 5\) 时，平均的解代价大约是 14，等等。当然，可以使用多种特征。例如，第二个特征\(x_2(n)\)可能是“在当前状态相邻而在目标状态中不相邻的滑块对的数量”。

• 如何对\(x_1(n)\)和\(x_2(n)\)进行组合来预测\(h_(n)\)？一种常见的方法是线性组合：

  \[h(n) = c_1x_1(n) + c_2x_2(n) \]

  可以调整常数\(c_1\)和\(c_2\)以适应随机生成的配置中实际数据的值。我们希望\(c_1\)和\(c_2\)都是正值，因为错位滑块和不正确的相邻对都会使得问题更难求解。注意，这个启发式函数满足目标状态\(h(n) = 0\)的条件，但它不一定是可容许的或一致的。