文献与代码管理工具及统计基础

文献与代码管理工具及统计基础

---

学习方法：好好上网，文献与代码管理工具
1.好好上网
2.Mendeley
3.github

1.好好上网，好好学习，好好提问

上网入口：搜索引擎(Google、Bing)
查文献：
问问题：提出一个好的问题

• 用什么工具上网？
• 用什么工具搜索？为什么学会上网很重要，尤其在学习深度学习的过程中
• stackoverflow
• 知乎
• csdn，比如说支持向量机的三重境界

2.学习资源整理

学习资源几类 (每一个层次都需要动手做实践)

• 视频

  • 万门，网易云课堂，coursera, Udacity

• 教科书

  • 周志华老师《机器学习》(南大教授)
  • Ian Goodfellow 《深度学习》(生成对抗网络GAN的发明者)
  • W. Mckinney 《Python for data analysis》

  Notes：周老师的《机器学习》，业内又称“西瓜书”，是入门机器学习的一本比较好的教材。
  Ian Goodfellow 《深度学习》，国内有中文翻译版，建议有一定基础的去看。

• paper论文或者小章节 （理论基础较好者，在有志学习深度学习以及人工智能时，应多读paper, 比如说)

  • Sabour, S., Frosst, N., & Hinton, G. E. (2017). Dynamic Routing Between Capsules, (Nips). Retrieved from http://arxiv.org/abs/1710.09829
  • LeCun, Y. (n.d.). Gradient-based learning applied to document. https://doi.org/10.1109/5.726791
  • Covington, P., Adams, J., & Sargin, E. (2016). Deep Neural Networks for YouTube Recommendations. Proceedings of the 10th ACM Conference on Recommender Systems - RecSys ’16, 191–198. https://doi.org/10.1145/2959100.2959190
  • Ng, A. (2012). 8. The EM Algorithm. Machine Learning, 1(X), 139–172. https://doi.org/10.1007/978-3-642-21551-3_6

文献管理工具

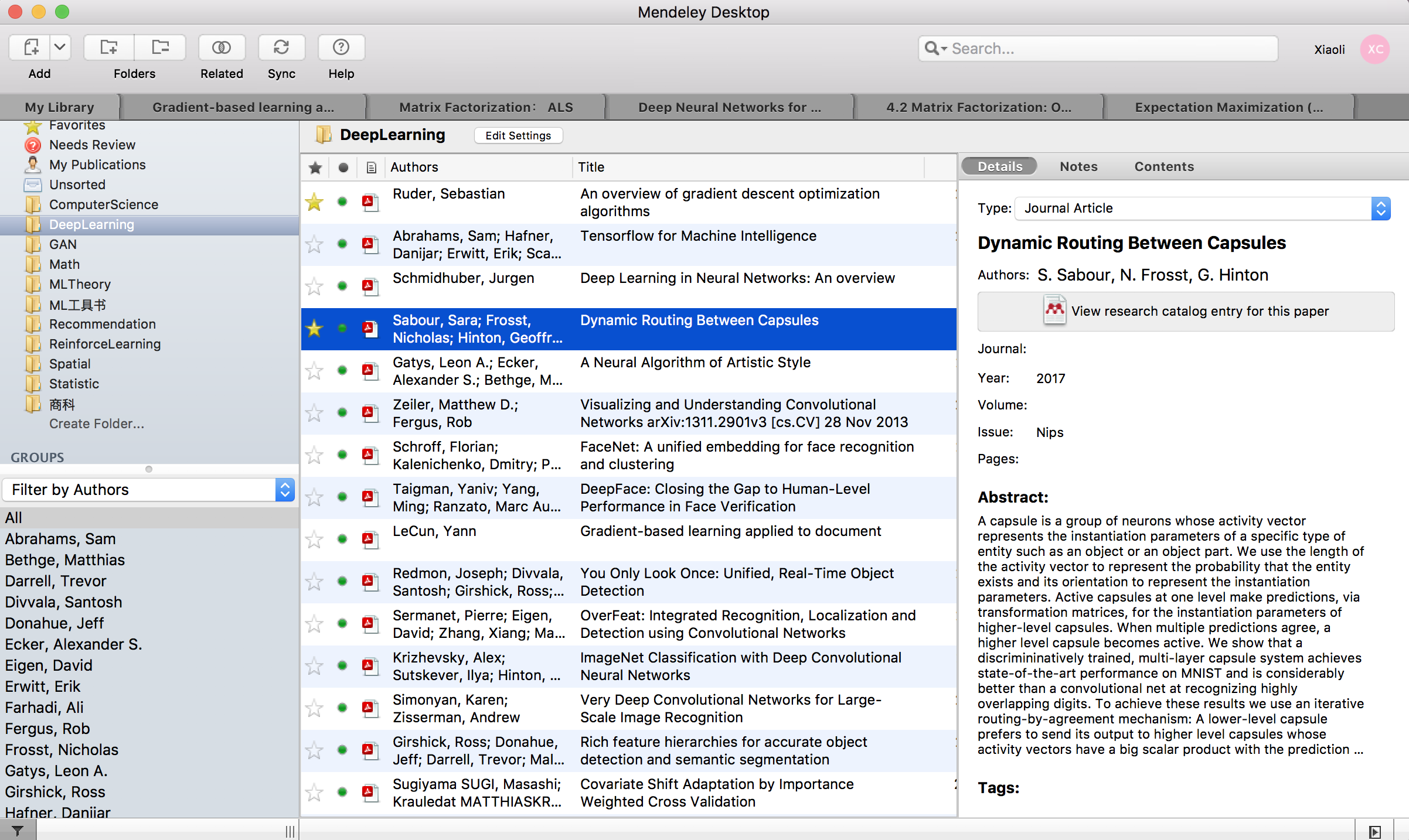
3. Github

3.1 Github安装

3.1.1 windows系统

1. 下载Git
   下载地址：http://git-scm.com/download/win 选择对应的版本，windows系统一般为64位系统，可以根据自己电脑的配置进行选择。

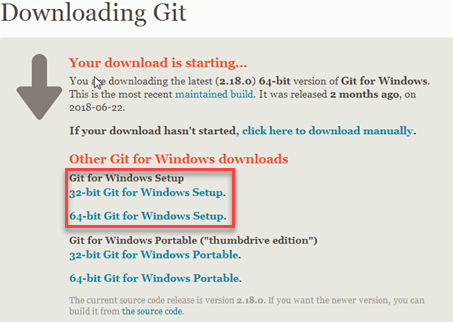
2. 安装Git
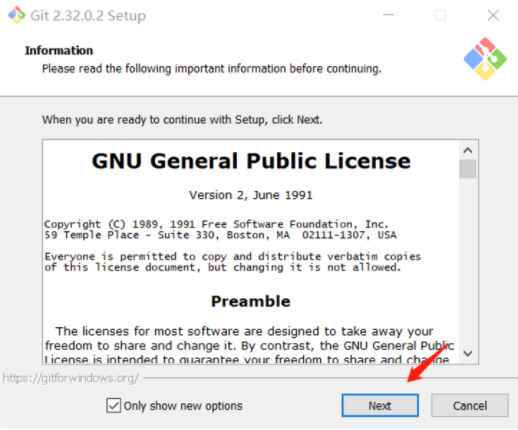
   下载完成后，双击下载好的软件开始安装，出现如下对话框，点击next

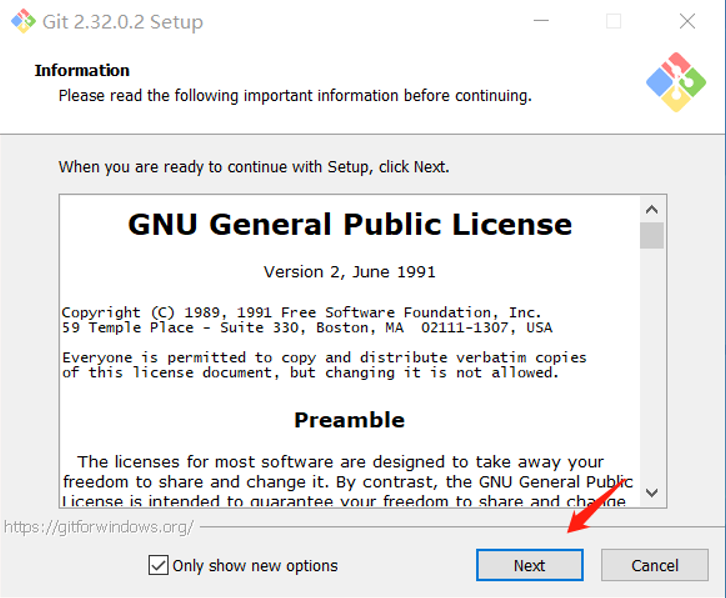
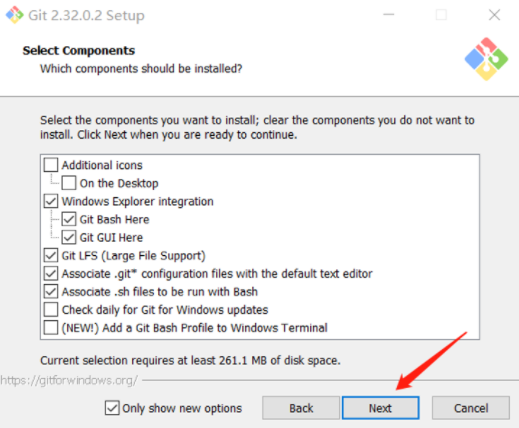
Git Bash Here和Git GUI Here可以方便的在任意目录下打开git，建议选中后，点击Next，不爱折腾的小伙伴下面的步骤可以直接采用默认选项，一路Next直到安装完成

点击Inall开始安装，安装完成后点击Finish就可以啦。

3.1.2 macOS系统

macOS系统的安装可以下图中参考来自平台用户热心的经验分享，对此表示非常感谢~

3.1.3 Linux系统

首先，你可以试着输入git，看看系统有没有安装Git：

~$ git
The program 'git' is currently not installed. You can install it by typing:
sudo apt-get install git

像上面的命令，有很多Linux会友好地告诉你Git没有安装，还会告诉你如何安装Git。
打开Linux终端，接着输入提示消息：

~$ sudo apt-get install git

输入用户密码，看到提示消息即说明已完成安装：

[sudo] xxxxxx 的密码：
正在读取软件包列表... 完成
正在分析软件包的依赖关系树       
正在读取状态信息... 完成       
git 已经是最新版

Github是程序员必备工具，作为版本控制(version control)和协同合作的利器，让人爱不释手。

• 几个概念：
  • 缓存区
  • 代码库
  • 本地
  • 远端

1. 安装github for windows, 注册账户
2. 基本命令
   • git init, 建一个新的repository
   • git clone 克隆一个repository
   • git add 加入新的内容到缓存区
   • git commit 实际提交改动
   • git push 推送改动到远端
   • git checkout -b 做一个分支branch
   • git pull 获取并合并远端的版本 （fetch+merge)
   • git merge 合并其他版本, 遇到冲突怎么办？
   • git log 查看记录

参考资料

几个名词：工作区(workspace)，暂存区(index)，代码库(Repository)，远端(Remote)

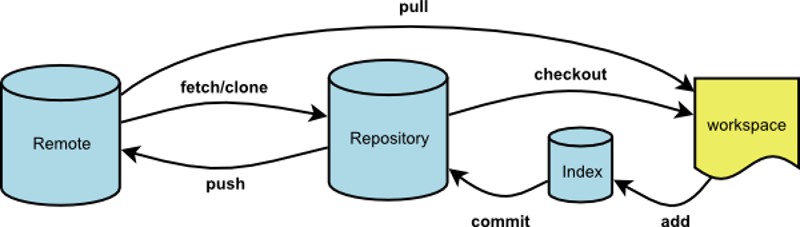
3.2 github的workflow

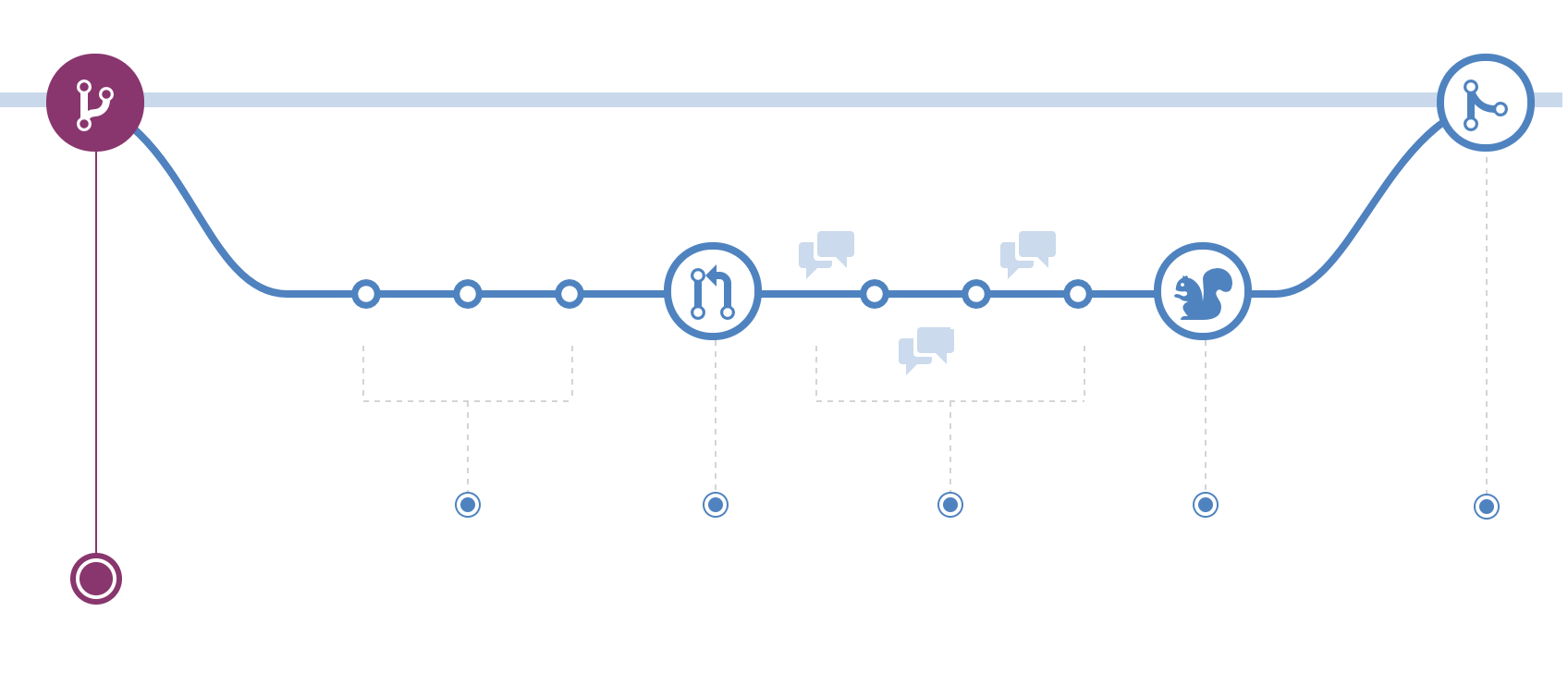
1. 在主干master之外，建立新的branch
2. 在本地修改，提交到暂存区
3. 提交pull requests
4. 群组讨论，进一步修改
5. merge到master上面

3.3 上手练练

参考

• Step1. 建立新的repository (本机)

1.1 本机建立repository: 在命令行中新建一个文件夹，进入文件夹后，使用git init进行初始化

1.2 添加一点文字文档内容，对本文件夹进行一定改动

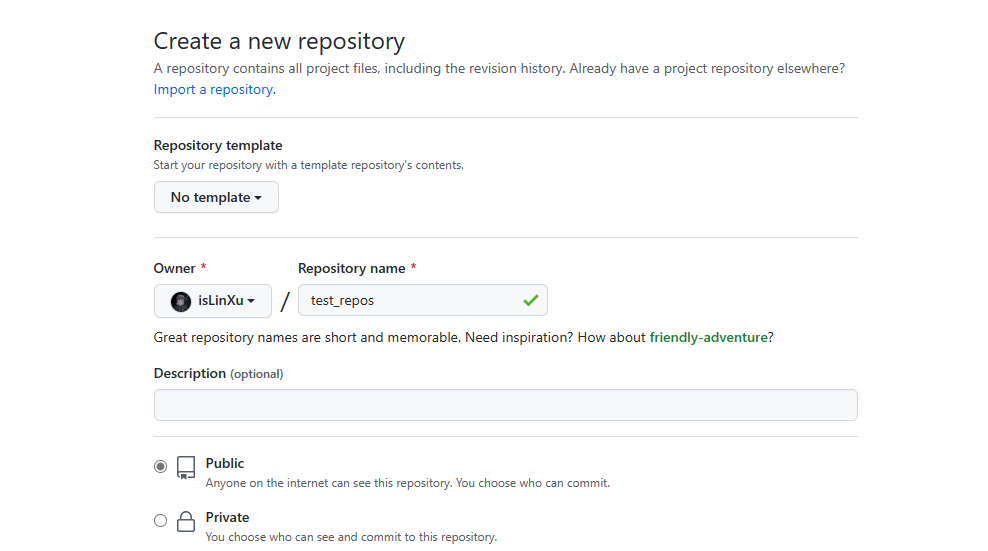
• Step2. 在远端建立repository, 并保存远端地址

• Step3. 保存远端地址, 并在本地的command line命令行工具中，添加远端地址，这样就把本地和远端链接起来了

• Step4. 将变动推送到主干master上

• Step5. 创建新的分支branch, 同时进入该新branch

• Step6. 查看过去记录

下面开始

生成并配置配置Github的SSH公钥

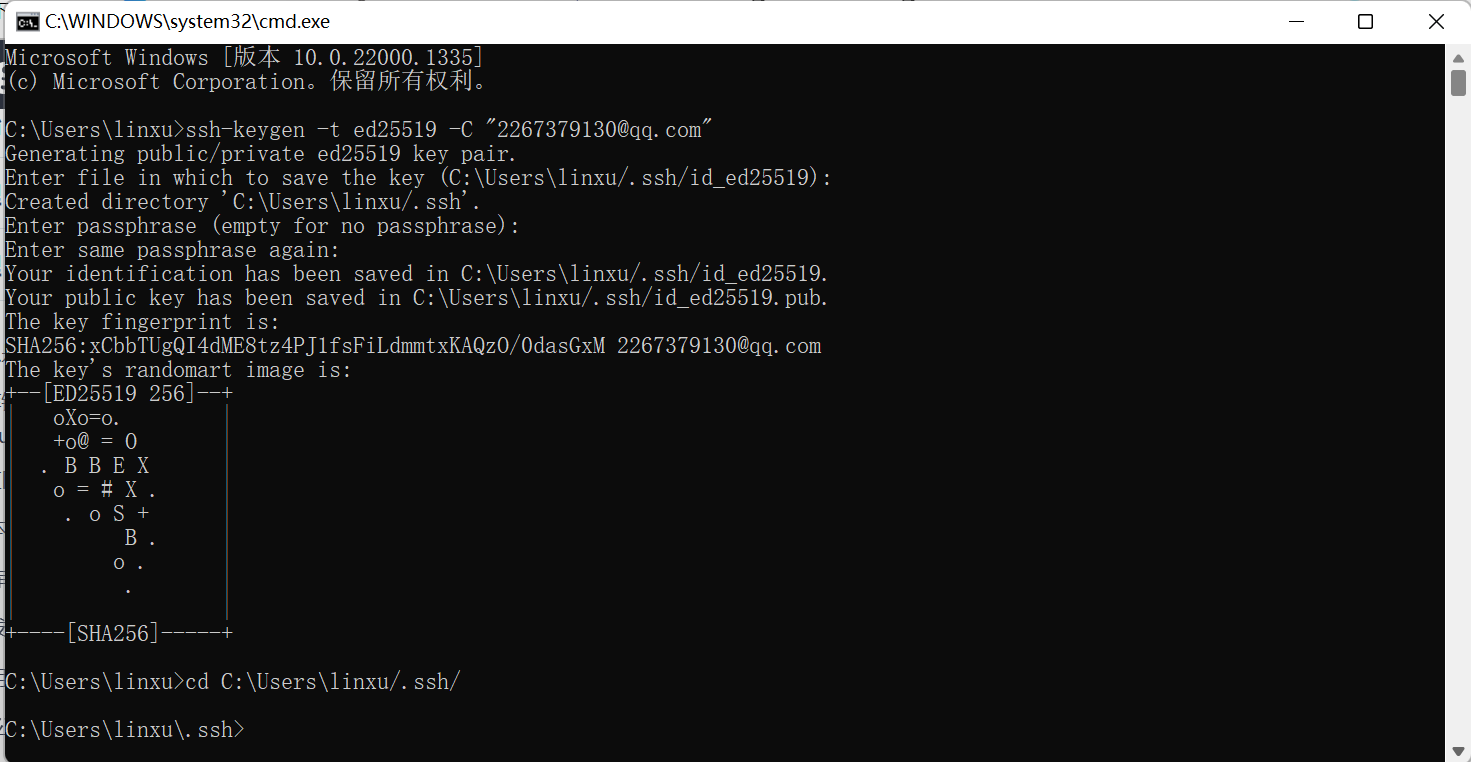
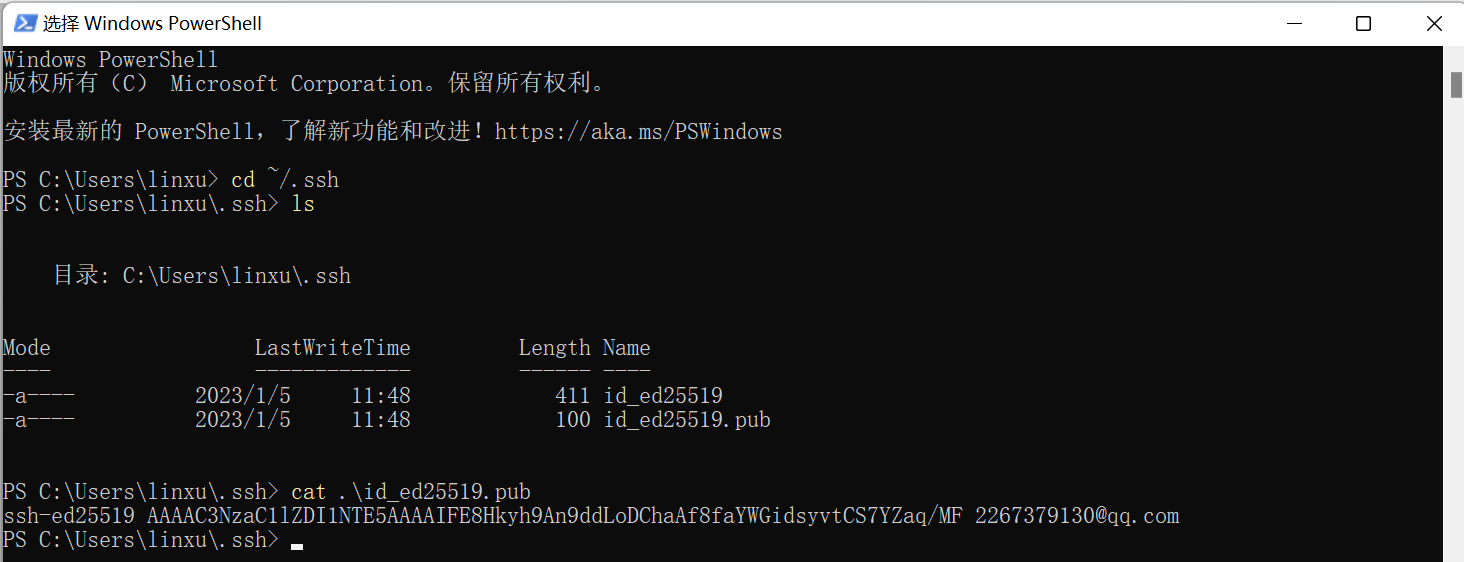
将\id_ed25519.pub文件中的内容复制出来，添加到Github上的SSH Key中，即可添加完毕。

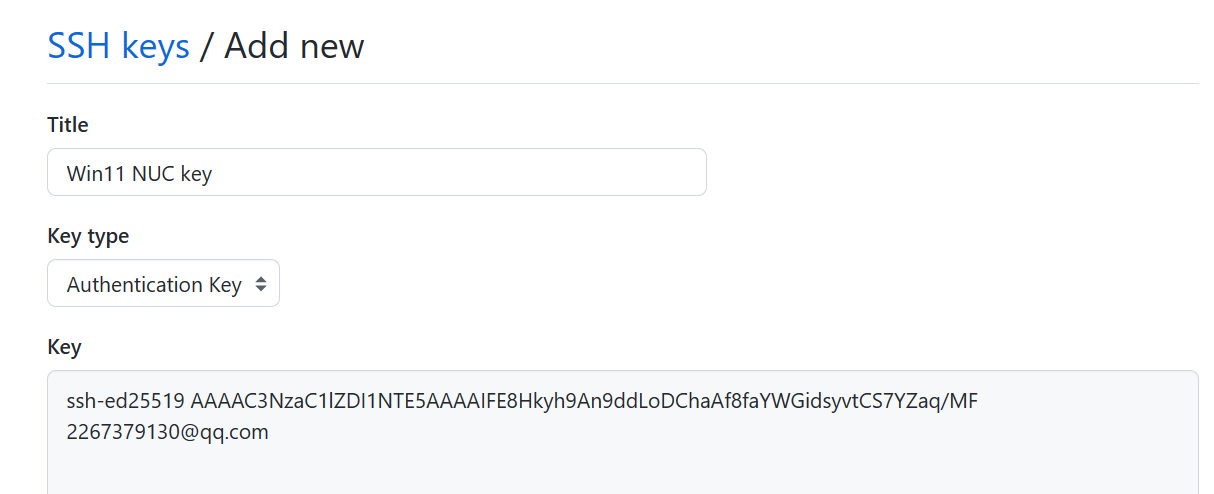
从https://github.com/settings/keys中可以查看。

Step1. 建立新的repository (本机)

• 从0开始，git init开始

1.1 本机建立repository: 在命令行中新建一个文件夹，进入文件夹后，使用git init进行初始化

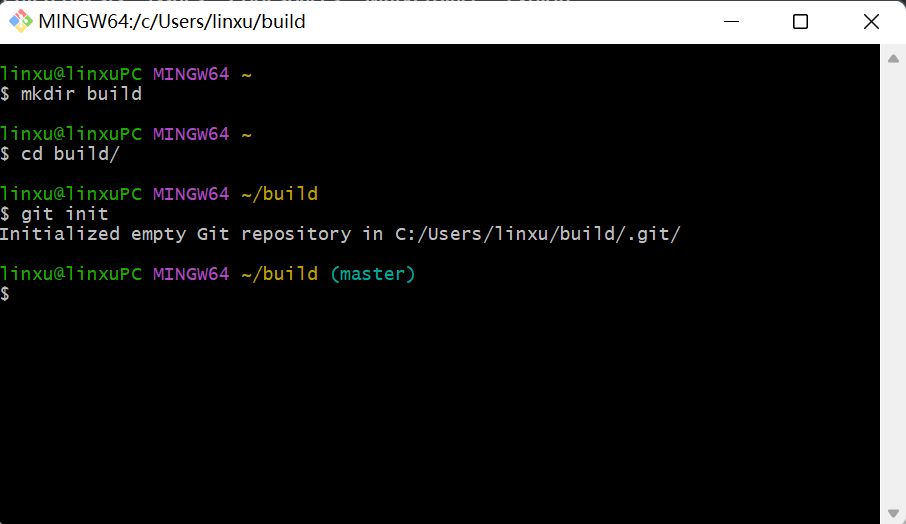
mkdir build

cd build

git init

1.2 添加一点文字文档内容，对本文件夹进行一定改动 使用jupyter notebook或者sublime或者记事本，在文件夹内新建一个文档，这时对本文件夹产生了变动.

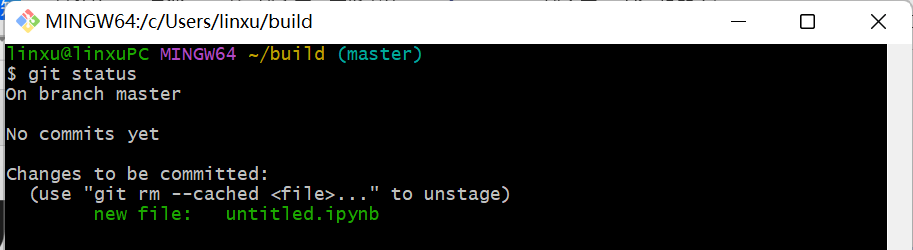
检查变动，使用

git status

1.3 将改动提交到暂存去，然后再交到代码库

将现有的文件夹中的改动都提交到暂存区

git add ./

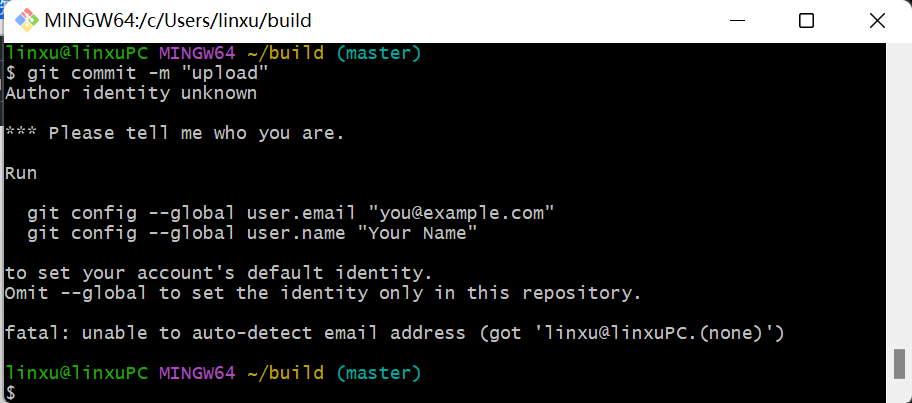
然后提交到代码库

git commit -m 'first commit‘

Step2. 在远端建立repository, 并保存远端地址 （需要先注册一个账号

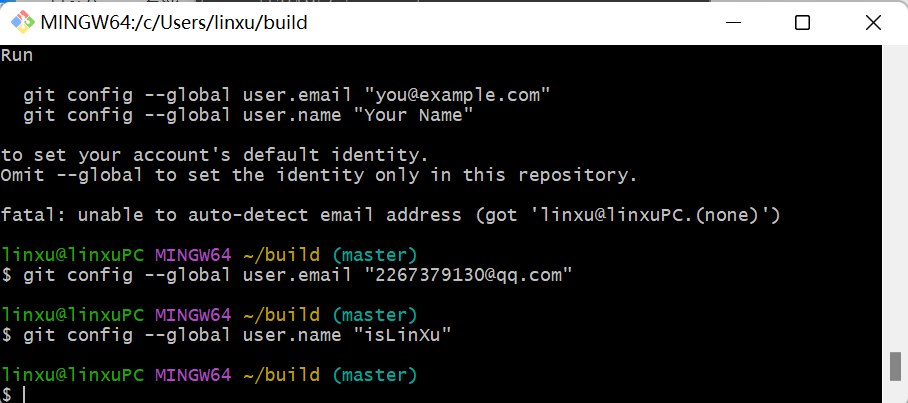
git config --global user.email "你的邮件地址"

git config --global user.name "你的用户名"

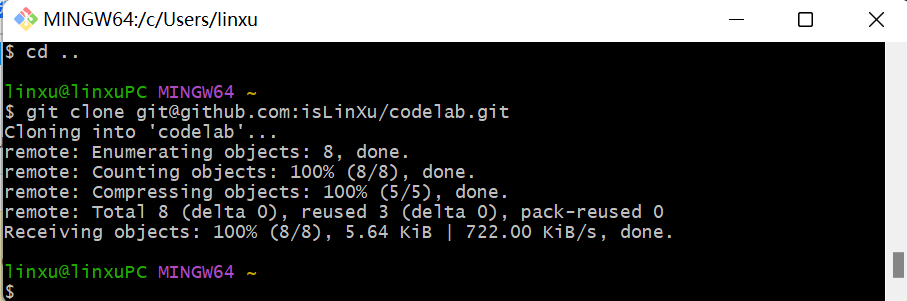
Step3. 保存远端地址, 并在本地的command line命令行工具中，添加远端地址，这样就把本地和远端链接起来了。要链接起来，还有更简单的方式，直接git clone

git remote add origin ---github.git---

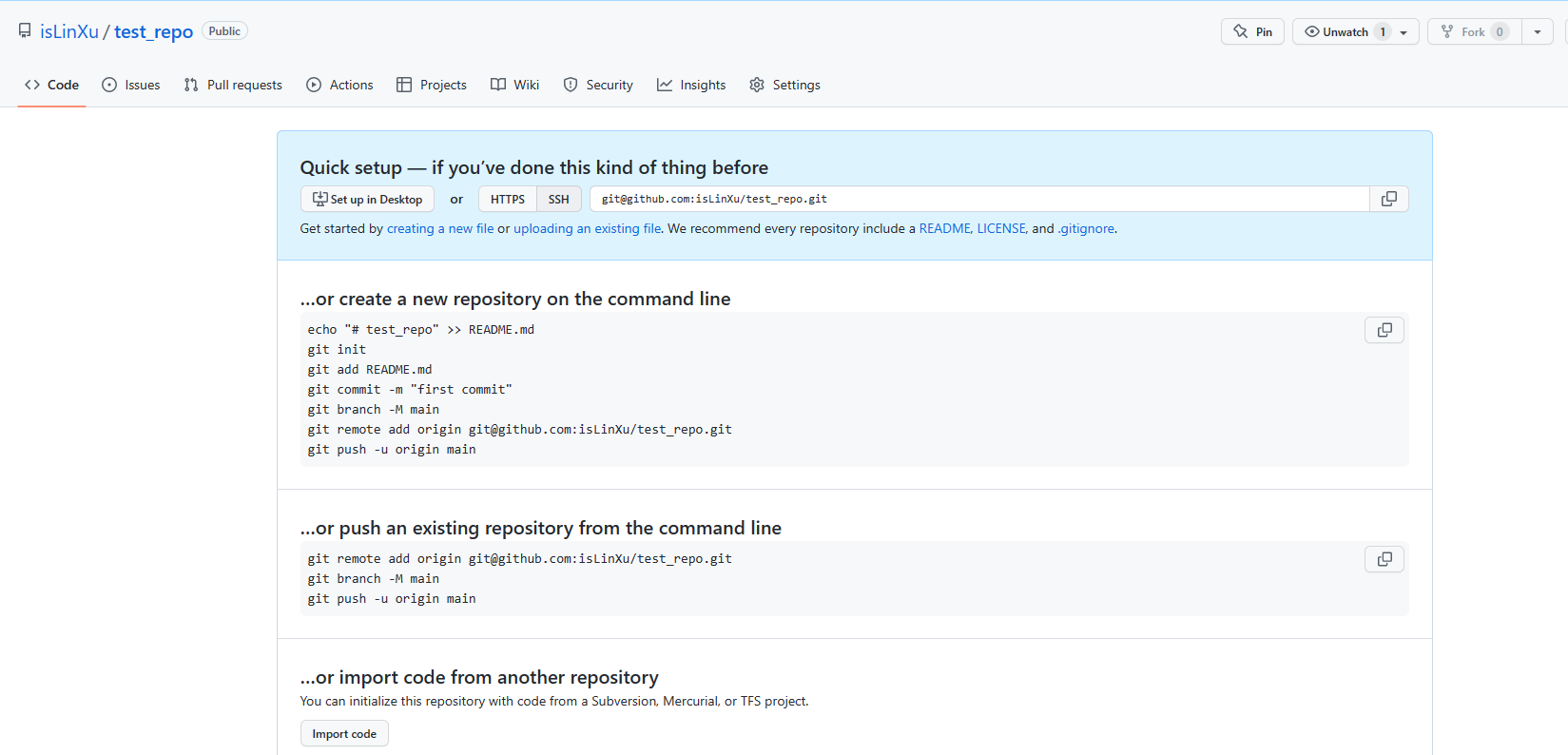
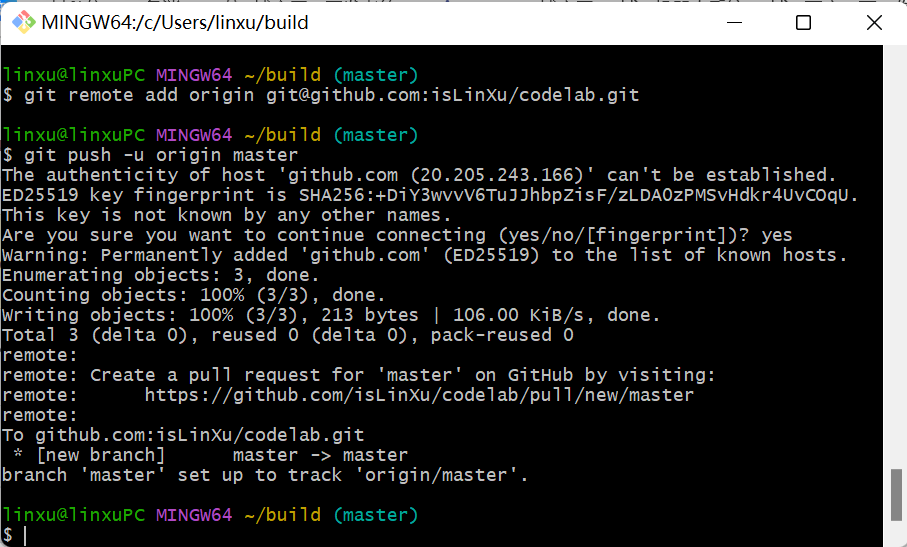
将变动推送到主干Master

git push -u origin master

• 这一步有更方便的办法，克隆已有的远端 repository，连最初的git initi也不用了，直接git clone ---远端的地址

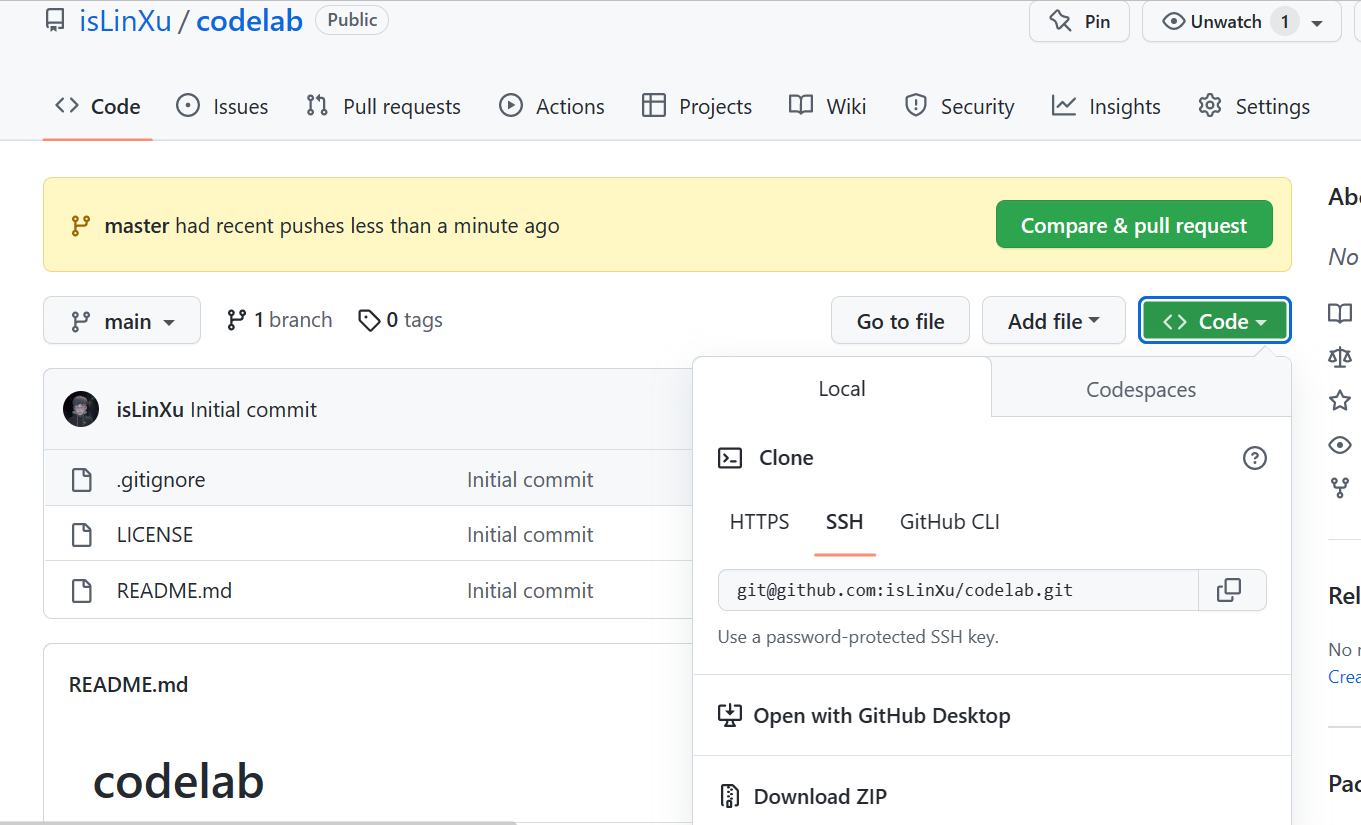
Step4. 将变动推送到主干master上

git push -u origin master

Step5. 创建新的分支branch, 同时进入该新branch

git checkout -b 'newbranch'

newbranch是新branch的名称，用户可以随意改动

如果要改回 master 主干，使用

git checkout master

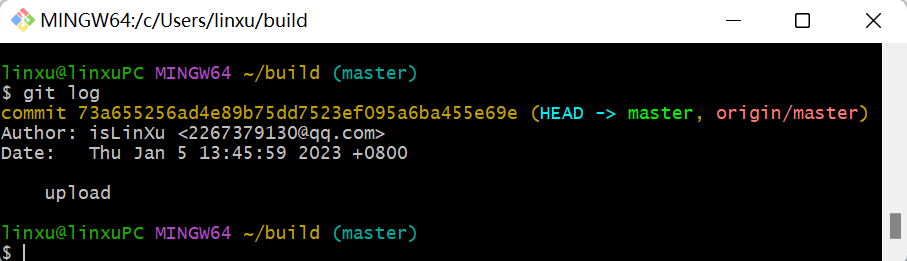
Step6. 查看过去记录

git log

这个是标准的查看过去记录的语句

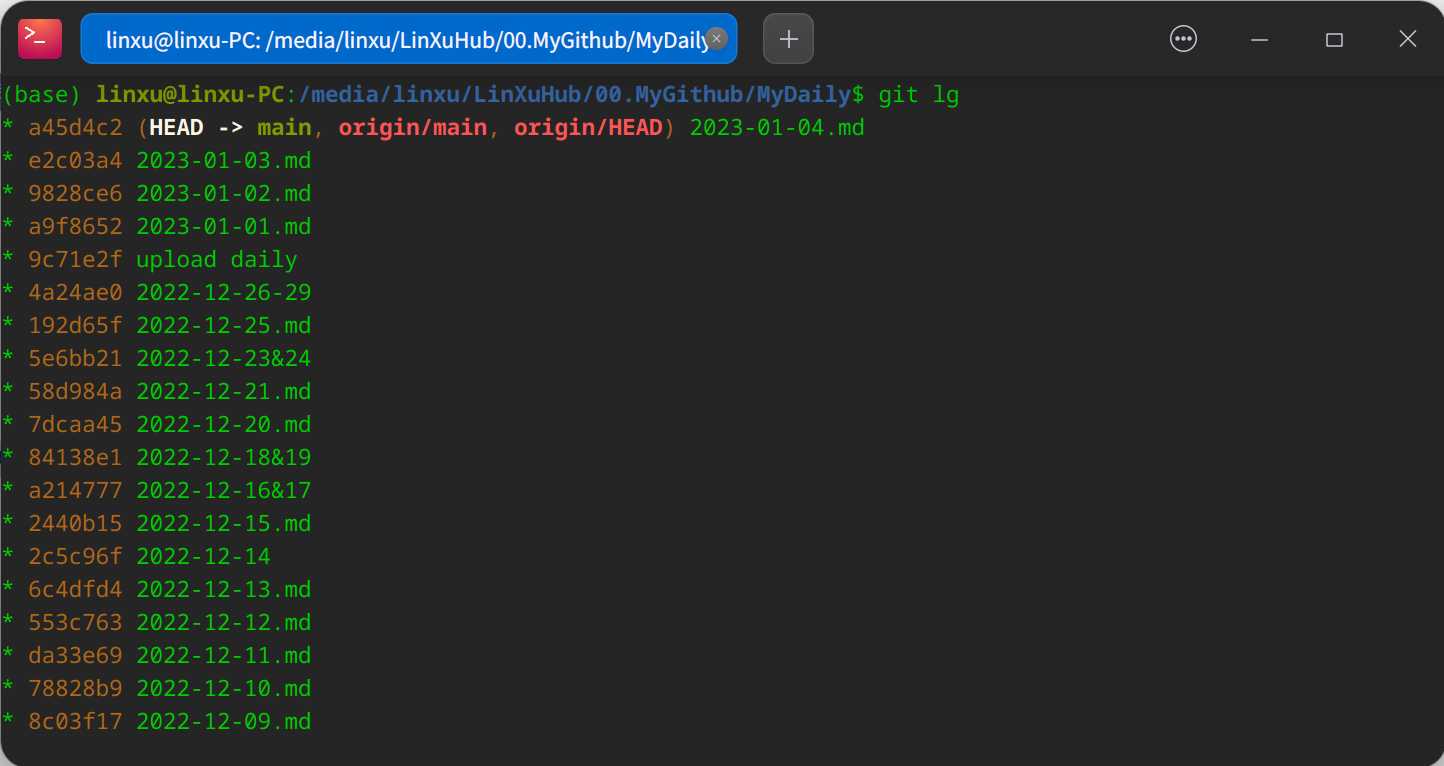
高级设置：过往分支记录可视化展示
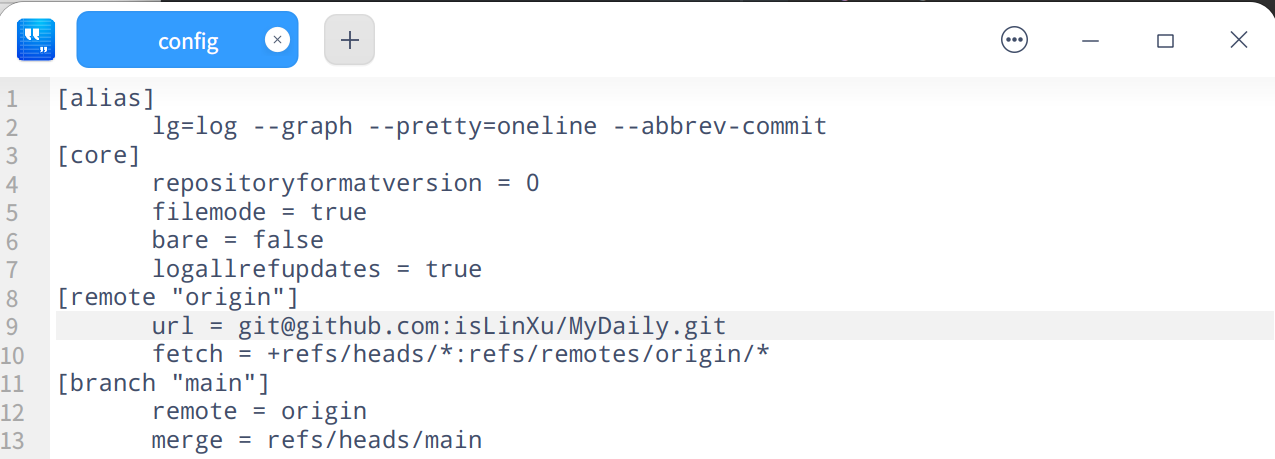
在HOME文件夹下，打开隐藏文件.gitconfig，没有就新建一个，内容如下：

[alias]
lg=log --graph --pretty=oneline --abbrev-commit

之后使用

git lg

查看可视化分支记录

合并分支并处理冲突

git merge

git的功能非常多，简单介绍了这几个，在以后工作中，还会有 git merge, git fetch, git pull, 等用法

统计基础

1. 均值
2. 方差
3. 大数定理
4. 中心极限定理
5. 假设检验
6. p-value定义

基础的均值与方差，在讨论回归的时候，很有意义，需要明确概念

我们在讨论假设检验的时候，先不要引入具体的概率分布，不要想t-分布, 而是直接从原假设与备择假设上面考虑。

1.均值

\[\begin{equation*} \bar{X}_n=\frac{1}{n}\left(\sum_{k=1}^n X_k\right) \end{equation*} \]

连续整体的期望值是

\[\begin{equation*} \mu = E\left(X\right) = \int xp(x)dx \end{equation*} \]

2.样本的方差

\[\begin{equation*} S^2 = \frac{1}{n-1}\sum_{i=1}^n\left(X_i-\bar{X}\right)^2 \end{equation*} \]

整体的方差

\[\begin{equation*} Var(X) = \sigma^2 = \int \left(x-\mu\right)^2 f(x)dx \end{equation*} \]

\[\begin{equation*} Var(X) = E[(X-\mu)^2] = E(X^2) - E^2(X) \end{equation*} \]

3.大数定理

样本数量越多，则其平均就越趋近期望值

\[\begin{equation*} n\rightarrow \infty, \bar{X}_n \rightarrow \mu \end{equation*} \]

4.中心极限定理

中心极限定理说明，在适当的条件下，大量相互独立随机变量的均值经适当标准化后依分布收敛于正态分布。

5.假设检验

6.p-value 最具争议的统计概念 定义：在原假设成立的情况，出现观测值以及更极端情况的概率