【论文阅读】AlexNet-ImageNet Classification with Deep Convolutional Neural Networks

ImageNet Classification with Deep Convolutional Neural Networks

Alex Krizhevsky University of Toronto kriz@cs.utoronto.ca
Ilya Sutskever University of Toronto ilya@cs.utoronto.ca
GeoffreyE. Hinton University of Toronto hinton@cs.utoronto.ca

Abstract

We trained a large, deep convolutional neural network to classify the 1.2 million high-resolution images in the ImageNet LSVRC-2010 contest into the 1000 different classes. On the test data, we achieved top-1 and top-5 error rates of 37.5% and 17.0% which is considerably better than the previous state-of-the-art. The neural network, which has 60 million parameters and 650,000 neurons, consists of five convolutional layers, some of which are followed by max-pooling layers, and three fully-connected layers with a final 1000-way softmax. To make training faster, we used non-saturating neurons and a very efficient GPU implementation of the convolution operation. To reduce overfitting in the fully-connected layers we employed a recently-developed regularization method called “dropout” that proved to be very effective. We also entered a variant of this model in the ILSVRC-2012 competition and achieved a winning top-5 test error rate of 15.3%, compared to 26.2% achieved by the second-best entry.

本文训练了一个大规模的深度卷积神经网络来将ImageNet LSVRC-2010比赛中的包含120万幅高分辨率的图像数据集分为1000种不同类别。在测试集上，本文所得的top-1和top-5错误率分别为37.5%和17.0%，该测试结果大大优于当前的最佳水平。本文的神经网络包含6千万个参数和65万个神经元，包含了5个卷积层，其中有几层后面跟着最大池化（max-pooling）层，以及3个全连接层，最后还有一个1000路的softmax层。为了加快训练速度，本文使用了不饱和神经元以及一种高效的基于GPU的卷积运算方法。为了减少全连接层的过拟合，本文采用了最新的正则化方法“dropout”，该方法被证明非常有效。我们以该模型的变体参加了ILSVRC-2012比赛，相比第二名26.2%，我们以15.3%的top-5测试错误率获胜。

1 Introduction

Current approaches to object recognition make essential use of machine learning methods. To improve their performance, we can collect larger datasets, learn more powerful models, and use better techniques for preventing over fitting. Until recently, datasets of labeled images were relatively small — on the order of tens of thousands of images (e.g., NORB [16], Caltech-101/256 [8, 9], and CIFAR-10/100 [12]). Simple recognition tasks can be solved quite well with datasets of this size, especially if they are augmented with label-preserving transformations. For example, the current best error rate on the MNIST digit-recognition task (<0.3%) approaches human performance [4]. But objects in realistic settings exhibit considerable variability, so to learn to recognize them it is necessary to use much larger training sets. And indeed, the shortcomings of small image datasets have been widely recognized (e.g., Pinto et al [21]), but it has only recently become possible to collect labeled datasets with millions of images. The new larger datasets include LabelMe [23], which consists of hundreds of thousands of fully-segmented images, and ImageNet [6], which consists of over 15 million labeled high-resolution images in over 22,000 categories.

当前目标识别的方法基本都使用了机器学习的方法。为了提高这些方法的性能，我们可以收集更大的数据集，学习得到更加强大的模型，然后使用更好的方法防止过拟合。直到现在，相比于成千上百的图像，带标签的图像数据集相对较小（如NORB[16]，Caltech-101/256[8,9]，以及CIFAR-10/100[12]）。这种规模的数据集能使得简单的识别任务得到很好地解决，特别是如果他们进行带标签的转换来增广数据集。例如，当前MINIST数字识别任务最小的错误率（<0.3% ）已经接近人类水平[4]。但是现实世界中的目标呈现出相当大的变化性，因此学习去识别它们就必须要使用更大的训练数据集。事实上，人们也已广泛地认识到小图像数据集的缺点（如Pinto等[21]），但直到最近，收集包含数百万图像的带标签数据集才成为可能。新的更大的数据集包括由数十万张全分割图像的LabelMe[23]和包含超过22000类的1500万张带标签高分辨率图像ImageNet[6]组成。

To learn about thousands of objects from millions of images, we need a model with a large learning capacity. However, the immense complexity of the object recognition task means that this problem cannot be specified even by a dataset as large as ImageNet, so our model should also have lots of prior knowledge to compensate for all the data we don’t have. Convolutional neural networks (CNNs) constitute one such class of models [16, 11, 13, 18, 15, 22, 26]. Their capacity can be controlled by varying their depth and breadth, and they also make strong and mostly correct assumptions about the nature of images (namely, stationarity of statistics and locality of pixel dependencies). Thus, compared to standard feedforward neural networks with similarly-sized layers, CNNs have much fewer connections and parameters and so they are easier to train, while their theoretically-best performance is likely to be only slightly worse.

为了从数以百万计的图像中学习出数千种的目标，我们需要一个具有很强学习能力的模型。然而，目标识别任务的巨大复杂性意味着，即使在ImageNet这样大的数据集也不能完成任务，因此我们的模型也要有许多先验知识来弥补所有我们没有的数据。卷积神经网络（CNNs）就形成了一种这样类别的模型[16，11,13,18,15,22,26]。可以通过改变网络的深度和广度控制CNN的学习能力，并且它们都能对图像的本质做出强大而又正确的判别（即统计的稳定性和像素位置的依赖性）。因此，相比于相似大小的标准前馈神经网络，CNNs的连接和参数更少，因此更易训练，尽管它们理论上的最优性能可能略差点。
Despite the attractive qualities of CNNs, and despite the relative efficiency of their local architecture, they have still been prohibitively expensive to apply in large scale to high-resolution images. Luckily, current GPUs, paired with a highly-optimized implementation of 2D convolution, are powerful enough to facilitate the training of interestingly-large CNNs, and recent datasets such as ImageNet contain enough labeled examples to train such models without severe overfitting.

尽管CNNs具有一些新颖的特性，和更有效率的局部结构，但大规模地应用于高分辨率图像消耗资源仍然过多。幸运的是，如今GPU以及高度优化的二维卷积计算，已经足够强大地去帮助大规模CNNs的训练，并且最新的数据集如ImageNet包含足够多的带标签样本，能够训练出不会严重过拟合的模型。
The specific contributions of this paper are as follows: we trained one of the largest convolutional neural networks to date on the subsets of ImageNet used in the ILSVRC-2010 and ILSVRC-2012 competitions [2] and achieved by far the best results ever reported on these datasets. We wrote a highly-optimized GPU implementation of 2D convolution and all the other operations inherent in training convolutional neural networks, which we make available publicly1. Our network contains a number of new and unusual features which improve its performance and reduce its training time, which are detailed in Section3. The size of our network made overfitting a significant problem, even with 1.2 million labeled training examples, so we used several effective techniques for preventing overfitting, which are described in Section 4. Our final network contains five convolutional and three fully-connected layers, and this depth seems to be important: we found that removing any convolutional layer (each of which contains no more than 1% of the model’s parameters) resulted in inferior performance.

本文具体贡献如下：基于ILSVRC-2010和ILSVRC-2012比赛中用到的ImageNet的子集本文训练出了至今为止一个最大的卷积神经网络[2]并且得到了迄今基于这些数据集最好的结果。本文实现了一种高度优化的二维卷积的GPU运算以及卷积神经网络训练中所有其他运算，这些都已公开提供；本文网络中包含了大量的不常见和新的特征来提升网络性能，减少训练时间，详见第三节；即使有120万带标签的训练样本，网络的大小使得过拟合仍成为一个严重的问题，因此本文使用了许多有效的防止过拟合的技术，详见第四节；本文最终的网络包含五层卷积层和三层全连接层，而这个深度似乎很重要：我们发现移除任何一层卷积层（每一层包含的参数个数不超过整个模型参数个数的1%）都会导致较差的结果。

In the end, the network’s size is limited mainly by the amount of memory available on current GPUs and by the amount of training time that we are willing to tolerate. Our network takes between five and six days to train on two GTX 580 3GB GPUs. All of our experiments suggest that our results can be improved simply by waiting for faster GPUs and bigger datasets to become available.

最后，网络的大小主要受限于GPU的内存大小和我们愿意忍受的训练时间长度。本文的网络在两个GTX 580 3GB GPU上训练了五到六天。本文所有的实验表明，如果有更快的GPU、更大的数据集，结果可以更好。

2 The Dataset

ImageNet is a dataset of over 15 million labeled high-resolution images belonging to roughly 22,000 categories. The images were collected from the web and labeled by human labelers using Amazon’s Mechanical Turk crowd-sourcing tool. Starting in 2010, as part of the Pascal Visual Object Challenge, an annual competition called the ImageNet Large-Scale Visual Recognition Challenge (ILSVRC) has been held. ILSVRC uses a subset of ImageNet with roughly 1000 images in each of 1000 categories. In all, there are roughly 1.2 million training images, 50,000 validation images, and 150,000 testing images.

ImageNet数据集包含有大概22000种类别共150多万带标签的高分辨率图像。这些图像是从网络上收集得来，由亚马逊的Mechanical Turkey的众包工具进行人工标记。从2010年开始，作为Pascal视觉目标挑战的一部分，ImageNet大规模视觉识别挑战（ImageNet Large-Scale Visual Recognition Challenge ，ILSVRC）比赛每年都会举行。ILSVRC采用ImageNet的子集，共包含一千个类别，每个类别包含大约1000幅图像。总的来说，大约有120万张训练图像，5万张验证图像以及15万张测试图像。

ILSVRC-2010 is the only version of ILSVRC for which the test set labels are available, so this is the version on which we performed most of our experiments. Since we also entered our model in the ILSVRC-2012 competition, in Section 6 we report our results on this version of the dataset as well, for which test set labels are unavailable. On ImageNet, it is customary to report two error rates: top-1 and top-5, where the top-5 error rate is the fraction of test images for which the correct label is not among the five labels considered most probable by the model.

ILSVRC-2010是ILSVRC唯一一个测试集标签公开的版本，因此这个版本就是本文大部分实验采用的数据集。由于我们也以我们的模型参加了ILSVRC-2012的比赛，在第6节本文也会列出在这个数据集上的结果，该测试集标签不可获取。ImageNet通常使用两种错误率：top-1和top-5，其中top-5错误率是指正确标签不在模型认为最有可能的前五个标签中的测试图像的百分数。

ImageNet consists of variable-resolution images, while our system requires a constant input dimensionality. Therefore, we down-sampled the images to a fixed resolution of 256 × 256. Given a rectangular image, we first rescaled the image such that the shorter side was of length 256, and then cropped out the central 256×256 patch from the resulting image. We did not pre-process the images in any other way, except for subtracting the mean activity over the training set from each pixel. So we trained our network on the (centered) raw RGB values of the pixels.

ImageNet包含不同分辨率的图像，但是本文的模型要求固定的输入维度。因此，本文将这些图像下采样为256x256 。给定一幅矩形图像，本文采用的方法是首先重新调整图像使得短边长度为256，然后裁剪出中央256x256 的区域。除了将图像减去训练集的图像均值(训练集和测试集都减去训练集的图像均值)，本文不做任何其他图像预处理。因此本文直接在每个像素的原始RGB值上进行训练。

3 The Architecture

The architecture of our network is summarized in Figure 2. It contains eight learned layers — ve convolutional and three fully-connected. Below, we describe some of the novel or unusual features of our network’s architecture. Sections 3.1-3.4 are sorted according to our estimation of their importance, with the most important first.
本文网络结构详见图2。它包含8层学习层——5层卷积层和三层全连接层。下面将描述该网络结构的一些创新和新的特征。3.1节至3.4节根据他们的重要性从大到小排序。

Figure 2: An illustration of the architecture of our CNN, explicitly showing the delineation of responsibilities between the two GPUs. One GPU runs the layer-parts at the top of the figure while the other runs the layer-parts at the bottom. The GPUs communicate only at certain layers. The network’s inputis150,528-dimensional, and the number of neurons in the network’s remaining layers is given by 253,440–186,624–64,896–64,896–43,264– 4096–4096–1000.

图2 本文CNN的结构图示，明确地描述了两个GPU之间的职责。一个GPU运行图上方的层，另一个运行图下方的层。两个GPU只在特定的层通信。网络的输入是150,528维的，网络剩余层中的神经元数目分别是253440，186624，64896，64896，43264，4096，4096，1000

3.1 ReLU Nonlinearity

The standard way to model a neuron’s output f as a function of its input x is with f(x) = tanh(x) or f(x) = (1 + e−x)−1. In terms of training time with gradient descent, these saturating nonlinearities are much slower than the non-saturating nonlinearity f(x) = max(0,x). Following Nair and Hinton [20], we refer to neurons with this nonlinearity as Rectified Linear Units (ReLUs). Deep convolutional neural networks with ReLUs train several times faster than their equivalents with tanh units. This is demonstrated in Figure 1, which shows the number of iterations required to reach 25% training error on the CIFAR-10 dataset for a particular four-layer convolutional network. This plot shows that we would not have been able to experiment with such large neural networks for this work if we had used traditional saturating neuron models.

通常使用一个关于输入x的函数模拟神经元的输出f，这种标准函数是f(x)=tanh(x)或者f(x)=(1+e−x)-1。在梯度下降训练时间上，这些饱和的非线性函数比不饱和非线性函数f(x)=max(0,x)f(x)=max(0,x)更慢。根据Nair和Hinton[20]，本文将具有这种非线性特征的神经元称为修正线性单元（ReLUs: Rectified Linear Units）。使用ReLUs的深度卷积神经网络训练速度比同样情况下使用tanh单元的速度快好几倍。图1表示使用特定的四层卷积网络在数据集CIFAR-10上达到25%错误率所需的迭代次数。这个图表明如果使用传统的饱和神经元模型我们不可能利用这么大规模的神经网络对本文工作进行试验。

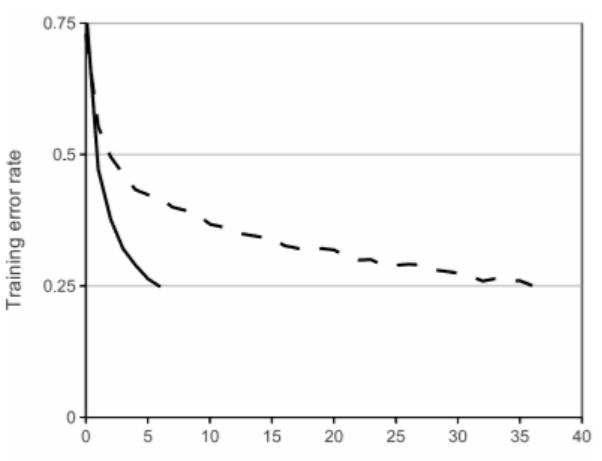
Figure 1: A four-layer convolutional neural network with ReLUs(solid line) reaches a 25% training error rate onCIFAR-10 six times faster than an equivalent network with tanh neurons (dashed line). The learning rates for each network were chosen in dependently to make training as fast as possible. No regularization of any kind was employed. The magnitude of the effect demonstrated here varies with network architecture, but networks with ReLUs consistently learn several times faster than equivalents with saturating neurons.

图1 使用ReLUs（实线）的四层卷积神经网络在CIFAR-10数据集上达到25%训练错误率比同等条件下使用tanh神经元（虚线）快6倍。为了尽可能使得训练速度快，每一个网络的学习速率都是独立选择的。任何一种都没有经过正则化。这里展示的效果的量级随着网络的结构而变化，但是利用ReLUs的网络始终比同等情况下使用饱和神经元的学习速度快很多倍。

We are not the first to consider alternatives to traditional neuron models in CNNs. For example, Jarrett et al.[11] claim that the nonlinearity f(x) = |tanh(x)| works particularly well with their type of contrast normalization followed by local average pooling on the Caltech-101 dataset. However, on this dataset the primary concern is preventing overfitting, so the effect they are observing is different from the accelerated ability to fit the training set which we report when using ReLUs. Faster learning has a great influence on the performance of large models trained on large datasets.

本文不是第一个考虑在CNNs中寻找传统神经模型替代方案的。例如，Jarrett等[11]考虑使用非线性函数f(x)=|tanh(x)|，在数据集Caltech-101上，与基于局部平均池化的对比归一化结合取得了很好地效果。但是，在这个数据集上他们主要关心的就是防止过拟合，而本文用ReLUs主要是对训练集的拟合进行加速。快速学习对由大规模数据集上训练出大模型的性能有相当大的影响。

3.2 Training on Multiple GPUs

A single GTX 580 GPU has only 3GB of memory, which limits the maximum size of the networks that can be trained on it. It turns out that 1.2 million training examples are enough to train networks which are too big to fit on one GPU. Therefore we spread the net across two GPUs. Current GPUs are particularly well-suited to cross-GPU parallelization, as they are able to read from and write to one another’s memory directly, without going through host machine memory. The parallelization scheme that we employ essentially puts half of the kernels (or neurons) on each GPU, with one additional trick: the GPUs communicate only in certain layers. This means that, for example, the kernels of layer 3 take input from all kernel maps in layer 2. However, kernels in layer 4 take input only from those kernel maps in layer 3 which reside on the same GPU. Choosing the pattern of connectivity is a problem for cross-validation, but this allows us to precisely tune the amount of communication until it is an acceptable fraction of the amount of computation.

单个GTX 580 GPU只有3GB的内存，从而限制了能由它训练出的网络的最大规模。实验表明使用120万训练样本训练网络已足够，但是这个任务对一个GPU来说太大了。因此，本文中的网络使用两个GPU。当前的GPU都能很方便地进行交叉GPU并行，因为它们可以直接相互读写内存，而不用经过主机内存。我们采用的并行模式本质上来说就是在每一个GPU上放二分之一的核(或者神经元)，我们还使用了另一个技巧：只有某些层才能进行GPU之间的通信。这就意味着，例如第三层的输入为第二层的所有特征图。但是，第四层的输入仅仅是第三层在同一GPU上的特征图。在交叉验证时，连接模式的选择是一个问题，而这个也恰好允许我们精确地调整通信的数量，直到他占计算数量的一个合理比例。

The resultant architecture is somewhat similar to that of the “columnar” CNN employed by Cires¸an et al.[5],except that our columns are not independent(seeFigure2). This scheme reduces our top-1 and top-5 error rates by 1.7% and 1.2%, respectively, as compared with a net with half as many kernels in each convolutional layer trained on one GPU. The two-GPU net takes slightly less time to train than the one-GPU net2.

最终的结构有点像Ciresan等[5]采用的柱状卷积神经网络，但是本文的列不是独立的（见图2）。与每个卷积层拥有本文一半的核,并且在一个GPU上训练的网络相比，这种组合让本文的top-1和top-5错误率分别下降了1.7%和1.2%。本文的2-GPU网络训练时间比一个GPU的时间都要略少。

3.3 Local Response Normalization

ReLUs have the desirable property that they do not require input normalization to prevent them from saturating. If at least some training examples produce a positive input to a ReLU, learning will happen in that neuron. However, we still find that the following local normalization scheme aids generalization. Denoting by aix,y the activity of a neuron computed by applying kernel i at position (x,y) and then applying the ReLU nonlinearity, the response-normalized activity bix,y is given by the expression

ReLUs具有符合本文要求的一个性质：它不需要对输入进行归一化来防止饱和。只要一些训练样本产生一个正输入给一个ReLU，那么在那个神经元中学习就会开始。但是，我们还是发现如下的局部标准化方案有助于增加泛化性能。aix,y表示使用核i作用于(x,y)然后再采用ReLU非线性函数计算得到的活跃度，那么响应标准化活跃bix,y由以下公式计算出.

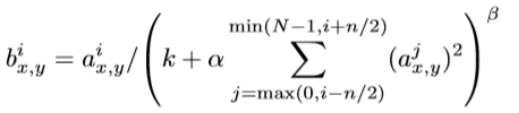
where the sum runs over n “adjacent” kernel maps at the same spatial position, and N is the total number of kernels in the layer. The ordering of the kernel maps is of course arbitrary and determined before training begins. This sort of response normalization implements a form of lateral inhibition inspired by the type found in real neurons, creating competition for big activities amongst neuron outputs computed using different kernels. The constants k,n,α, and β are hyper-parameters whose values are determined using a validation set; we used k = 2, n = 5, α = 10−4, and β = 0.75. We applied this normalization after applying the ReLU nonlinearity in certain layers (see Section 3.5).

这里，对同一个空间位置的n个邻接核特征图（kernel maps）求和，N是该层的核的总数目。核特征图的顺序显然是任意的，并且在训练之前就已决定了的。这种响应归一化实现了侧抑制的一种形式，侧抑制受启发于一种在真实神经中发现的形式，对利用不同核计算得到的神经输出之间的大的活跃度生成竞争。常数k,n,α,β是超参数，它们的值使用一个验证集来确定。本文使用k=2,n=5,α=10−4,β=0.75。本文在某些特定的层中，采用ReLUs非线性函数后应用了该归一化（见3.5节）。

This scheme bears some resemblance to the local contrast normalization scheme of Jarrett et al.[11], but ours would be more correctly termed “brightness normalization”, since we do not subtract the mean activity. Response normalization reduces our top-1 and top-5 error rates by 1.4% and 1.2%, respectively. We also verified the effectiveness of this scheme on the CIFAR-10 dataset: a four-layer CNN achieved a 13% test error rate without normalization and 11% with normalization3.

这个方案与Jarrett等[11]的局部对比度归一化方案有些相似，但本文更加准确的称呼为“亮度归一化”(brightness normalization)，因为本文没有减去平均活跃度。响应归一化将top-1和top-5的错误率分别降低了1.4%和1.2%。本文也在CIFAR-10数据集上验证了这个方案的有效性：一个四层的CNN网络在未归一化的情况下错误率是13%，在归一化的情况下是11%。

3.4 Overlapping Pooling

Pooling layers in CNNs summarize the outputs of neighboring groups of neurons in the same kernel map. Traditionally, the neighborhoods summarized by adjacent pooling units do not overlap (e.g., [17, 11, 4]). To be more precise, a pooling layer can be thought of as consisting of a grid of pooling units spaced s pixels apart, each summarizing a neighborhood of size z×z centered at the location of the pooling unit. If we set s = z, we obtain traditional local pooling as commonly employed in CNNs. If we set s < z, we obtain overlapping pooling. This is what we use throughout our network, with s = 2 and z = 3. This scheme reduces the top-1 and top-5 error rates by 0.4% and 0.3%, respectively, as compared with the non-overlapping scheme s = 2, z = 2, which produces output of equivalent dimensions. We generally observe during training that models with overlapping pooling find it slightly more difficult to overfit.

CNNs中的池化层归纳了同一个核特征图中的相邻神经元组的输出。通常，由邻接池化单元归纳的邻域并不重叠（例如，[17,11,4]）。更确切地说，一个池化层可以被看作是包含了每间隔S个像素的池化单元的栅格组成，每一个都归纳了以池化单元为中心大小为Z x Z的邻域。如果令S=Z，将会得到CNNs通常采用的局部池化。如果我们设置s <z，我们获得重叠池化。 这是我们在整个网络中使用的，s = 2和z = 3.与非重叠方案s =2, z= 2相比，该方案分别将top-1和top-5错误率分别降低0.4％和0.3％，产生等效尺寸的输出。 我们在训练期间观察到具有重叠池化的模型通常过度拟合稍微困难一些。

3.5 Overall Architecture

Now we are ready to describe the overall architecture of our CNN. As depicted in Figure 2, the net contains eight layers with weights; the first five are convolutional and the remaining three are fully connected. The output of the last fully-connected layer is fed to a 1000-way softmax which produces a distribution over the 1000 class labels. Our network maximizes the multinomial logistic regression objective, which is equivalent to maximizing the average across training cases of the log-probability of the correct label under the prediction distribution.

现在我们可以来描述本文CNN的整体结构。正如图2所示，这个网络包含八个有权值的层：前五层是卷积层，剩下的三层是全连接层。最后一个全连接层的输出传递给一个1000路的softmax层，这个softmax产生一个对1000类标签的分布。本文的网络最大化多项Logistic回归结果，也就是最大化训练集预测正确的标签的对数概率。

The kernels of the second, fourth, and fifth convolutional layers are connected only to those kernel maps in the previous layer which reside on the same GPU (see Figure 2). The kernels of the third convolutional layer are connected to all kernel maps in the second layer. The neurons in the fully connected layers are connected to all neurons in the previous layer. Response-normalization layers follow the first and second convolutional layers. Max-pooling layers, of the kind described in Section 3.4, follow both response-normalization layers as well as the fifth convolutional layer. The ReLU non-linearity is applied to the output of every convolutional and fully-connected layer.

第二、四、五层卷积层的核只和同一个GPU上的前层的核特征图相连（见图2）。第三层卷积层和第二层所有的核特征图相连接。全连接层中的神经元和前一层中的所有神经元相连接。响应归一化层跟着第一和第二层卷积层。最大池化层，3.4节中有所描述，既跟着响应归一化层也跟着第五层卷积层。ReLU非线性变换应用于每一个卷积和全连接层的输出。

The first convolutional layer filters the 224×224×3 input image with 96 kernels of size 11×11×3 with a stride of 4 pixels (this is the distance between the receptive field centers of neighboring neurons in a kernel map). The second convolutional layer takes as input the (response-normalized and pooled) output of the first convolutional layer and filters it with 256 kernels of size 5×5×48. The third, fourth, and fifth convolutional layers are connected to one another without any intervening pooling or normalization layers. The third convolutional layer has 384 kernels of size 3 × 3 × 256 connected to the (normalized, pooled) outputs of the second convolutional layer. The fourth convolutional layer has 384 kernels of size 3×3×192 , and the fifth convolutional layer has 256 kernels of size 3×3×192. The fully-connected layers have 4096 neurons each.

第一层卷积层使用96个大小为11x11x3的卷积核对224x224x3的输入图像以4个像素为步长（这是核特征图中相邻神经元感受域中心之间的距离）进行滤波。第二层卷积层将第一层卷积层的输出（经过响应归一化和池化）作为输入，并使用256个大小为5x5x48的核对它进行滤波。第三层、第四层和第五层的卷积层在没有任何池化或者归一化层介于其中的情况下相互连接。第三层卷积层有384个大小为3x3x256的核与第二层卷积层的输出（已归一化和池化）相连。第四层卷积层有384个大小为3x3x192的核，第五层卷积层有256个大小为 的核。每个全连接层有4096个神经元。

4 Reducing Overfitting

Our neural network architecture has 60 million parameters. Although the 1000 classes of ILSVRC make each training example impose 10 bits of constraint on the mapping from image to label, this turns out to be insufficient to learn so many parameters without considerable overfitting. Below, we describe the two primary ways in which we combat overfitting.
本文的神经网络结构有6千万个参数。尽管ILSVRC的1000个类别使得每一个训练样本利用10bit的数据就可以将图像映射到标签上，但是如果没有大量的过拟合，是不足以学习这么多参数的。接下来，本文描述了两种对抗过拟合的主要的方法。

4.1 Data Augmentation

The easiest and most common method to reduce overfitting on image data is to artificially enlarge the dataset using label-preserving transformations (e.g., [25, 4, 5]). We employ two distinct forms of data augmentation, both of which allow transformed images to be produced from the original images with very little computation, so the transformed images do not need to be stored on disk. In our implementation, the transformed images are generated in Python code on the CPU while the GPU is training on the previous batch of images. So these data augmentation schemes are, in effect, computationally free.
降低图像数据过拟合的最简单常见的方法就是利用标签转换人为地增大数据集（例如，[25,4,5]）。本文采取两种不同的数据增强方式，这两种方式只需要少量的计算就可以从原图中产生转换图像，因此转换图像不需要存入磁盘。本文中利用GPU训练先前一批图像的同时，使用CPU运行Python代码生成转换图像。因此这些数据增强方法实际上是不用消耗计算资源的。

The first form of data augmentation consists of generating image translations and horizontal reflections. We do this by extracting random 224×224 patches(and their horizontal reflections) from the 256×256 images and training our network on these extracted patches 4. This increases the size of our training set by a factor of 2048, though the resulting training examples are, of course, highly interdependent. Without this scheme, our network suffers from substantial overfitting, which would have forced us to use much smaller networks. At test time, the network makes a prediction by extracting five 224 × 224 patches (the four corner patches and the center patch) as well as their horizontal reflections (hence ten patches in all), and averaging the predictions made by the network’s softmax layer on the ten patches.

第一种数据增强的形式包括生成平移图像和水平翻转图像。做法就是从256x256的图像中提取随机的224x224大小的块（以及它们的水平翻转），然后基于这些提取的块训练网络。这个让我们的训练集增大了2048倍（(256-224)2*2=2048），尽管产生的这些训练样本显然是高度相互依赖的。如果不使用这个方法，本文的网络会有大量的过拟合，这将会迫使我们使用更小的网络。在测试时，网络通过提取5个224x224块（四个边角块和一个中心块）以及它们的水平翻转（因此共十个块）做预测，然后网络的softmax层对这十个块做出的预测取均值。

The second form of data augmentation consists of altering the intensities of the RGB channels in training images. Specifically, we perform PCA on the set of RGB pixel values throughout the ImageNet training set. To each training image, we add multiples of the found principal components, with magnitudes proportional to the corresponding eigenvalues times a random variable drawn from a Gaussian with mean zero and standard deviation 0.1. Therefore to each RGB image pixel Ixy = [IRxy,IGxy,IBxy]T we add the following quantity:

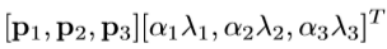
where pi and λi are ith eigenvector and eigenvalue of the 3 × 3 covariance matrix of RGB pixel values, respectively, and αi is the aforementioned random variable. Each αi is drawn only once for all the pixels of a particular training image until that image is used for training again, at which point it is re-drawn. This scheme approximately captures an important property of natural images, namely, that object identity is invariant to changes in the intensity and color of the illumination. This scheme reduces the top-1 error rate by over 1%.

第二种数据增强的形式包括改变训练图像的RGB通道的强度。特别的，本文对整个ImageNet训练集的RGB像素值进行了PCA。对每一幅训练图像，本文加上多倍的主成分，倍数的值为相应的特征值乘以一个均值为0标准差为0.1的高斯函数产生的随机变量。因此对每一个RGB图像像素Ixy=[IRxy,IGxy,IBxy]T加上如下的量

[P1,P2,P3][α1λ1,α2λ2,α3λ3]T

这里Pi,λi分别是RGB像素值的3x3协方差矩阵的第i个特征向量和特征值，αi是上述的随机变量。每一个αi的值对一幅特定的训练图像的所有像素是不变的，直到这幅图像再次用于训练，此时才又赋予αi新的值。这个方案得到了自然图像的一个重要的性质，也就是，改变光照的颜色和强度，目标的特性是不变的。这个方案将top-1错误率降低了1%。

4.2 Dropout

Combining the predictions of many different models is a very successful way to reduce test errors [1, 3], but it appears to be too expensive for big neural networks that already take several days to train. There is, however, a very efficient version of model combination that only costs about a factor of two during training. The recently-introduced technique, called “dropout” [10], consists of setting to zero the output of each hidden neuron with probability 0.5. The neurons which are “dropped out” in this way do not contribute to the forward pass and do not participate in backpropagation. So every time an input is presented, the neural network samples a different architecture, but all these architectures share weights. This technique reduces complex co-adaptations of neurons, since a neuron cannot rely on the presence of particular other neurons. It is, therefore, forced to learn more robust features that are useful in conjunction with many different random subsets of the other neurons. At test time, we use all the neurons but multiply their outputs by 0.5, which is a reasonable approximation to taking the geometric mean of the predictive distributions produced by the exponentially-many dropout networks.

结合多种不同模型的预测结果是一种可以降低测试误差的非常成功的方法[1,3]，但是这对于已经要花很多天来训练的大规模神经网络来说显得太耗费时间了。但是，有一种非常有效的模型结合的方法，训练时间只需要原先的两倍。最新研究的技术，叫做“dropout”[10]，它将每一个隐藏神经元的输出以50%的概率设为0。这些以这种方式被“踢出”的神经元不会参加前向传递，也不会加入反向传播。因此每次有输入时，神经网络采样一个不同的结构，但是所有这些结构都共享权值。这个技术降低了神经元之间复杂的联合适应性，因为一个神经元不是依赖于另一个特定的神经元的存在的。因此迫使要学到在连接其他神经元的多个不同随机子集的时候更鲁棒性的特征。在测试时，本文使用所有的神经元，但对其输出都乘以了0.5，对采用多指数dropout网络生成的预测分布的几何平均数来说这是一个合理的近似。

We use dropout in the first two fully-connected layers of Figure2. Without dropout, our network exhibits substantial overfitting. Dropout roughly doubles the number of iterations required to converge.
本文在图2中的前两个全连接层使用dropout。如果不采用dropout，本文的网络将会出现大量的过拟合。Dropout大致地使达到收敛的迭代次数增加了一倍。

5 Details of learning

We trained our models using stochastic gradient descent with a batch size of 128 examples, momentum of 0.9, and weight decay of 0.0005. We found that this small amount of weight decay was important for the model to learn. In other words, weight decay here is not merely a regularizer: it reduces the model’s training error. The update rule for weight w was

where i is the iteration index, is the momentum variable, is the learning rate, and is the average over the ith batch Di of the derivative of the objective with respect to w, evaluated at wi.
本文使用随机梯度下降来训练模型，同时设置batch size大小为128，0.9倍动量以及0.0005的权值衰减。我们发现这个很小的权值衰减对模型的学习很重要。换句话说，这里的权值衰减不只是一个正则化矩阵：它降低了模型的训练错误率。权重ω更新规则是

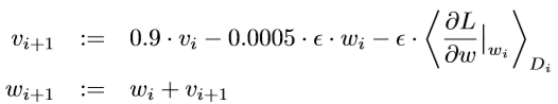
这里i是迭代索引，v是动量变量，ε是学习速率，是在点ωi，目标对ω求得的导数的第i个batch:Di的均值。

We initialized the weights in each layer from a zero-mean Gaussian distribution with standard deviation 0.01. We initialized the neuron biases in the second, fourth, and fifth convolutional layers, as well as in the fully-connected hidden layers, with the constant 1. This initialization accelerates the early stages of learning by providing the ReLUs with positive inputs. We initialized the neuron biases in the remaining layers with the constant 0.
本文对每一层的权值使用均值为0、标准差为0.01的高斯分布进行初始化。对第二层、第四层、第五层卷积层以及全连接的隐藏层使用常数1初始化神经元偏置项。这个初始化通过给ReLUs提供正输入加快了学习的初始阶段。本文对剩余的层使用常数0初始化神经元偏置项。

We used an equal learning rate for all layers, which we adjusted manually throughout training. The heuristic which we followed was to divide the learning rate by 10 when the validation error rate stopped improving with the current learning rate. The learning rate was initialized at 0.01 and reduced three times prior to termination. We trained the network for roughly 90 cycles through the training set of 1.2 million images, which took five to six days on two NVIDIA GTX580 3GB GPUs.
本文对所有层使用相同的学习速率，这个由在整个学习过程中手动地调整得到。我们采用启发式算法:当验证错误率停止降低就将当前学习速率除以10。本文的学习速率初始值设为0.01，在终止之前减小了三次。本文训练该网络对120万的图像训练集大约进行了90个周期，使用了两个NVIDIA GTX 580 3GB GPU，花费了5到6天的时间。

6 Results

Our results on ILSVRC-2010 are summarized in Table 1. Our network achieves top-1 and top-5 test set error rates of 37.5% and 17.0%5. The best performance achieved during the ILSVRC2010 competition was 47.1% and 28.2% with an approach that averages the predictions produced from six sparse-coding models trained on different features [2], and since then the best published results are 45.7% and 25.7% with an approach that averages the predictions of two classifiers trained on Fisher Vectors (FVs) computed from two types of densely-sampled features [24].
本文的在ILSVRC-2010上的结果见表1。本文网络的测试集top-1和top-5的错误率分别为37.5%和17.0%。在ILSVRC-2010比赛中最好的结果是47.1%和28.2%，采用的方法是对六个基于不同特征训练得到的稀疏编码模型的预测结果求平均数[2]，此后最好的结果是45.7%和25.7%，采用的方法是对基于从两种密集采样特征计算得到的Fisher向量（FVs），训练得到两个分类器，所得的预测结果求平均数[24]。

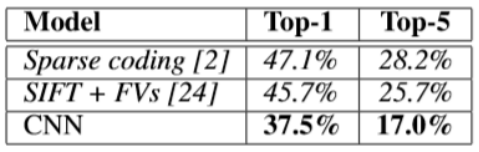
Table 1: Comparison of results on ILSVRC2010 test set. In italics are best results achieved by others.
表1 基于ILSVRC-2010测试集的结果对比。斜体字是其他方法获得的最好结果

We also entered our model in the ILSVRC-2012 competition and report our results in Table 2. Since the ILSVRC-2012 test set labels are not publicly available, we cannot report test error rates for all the models that we tried. In the remainder of this paragraph, we use validation and test error rates interchangeably because in our experience they do not differ by more than 0.1% (seeTable2). The CNN described in this paper achieves a top-5 error rate of 18.2%. Averaging the predictions of five similar CNNs gives an error rate of 16.4%. Training one CNN, with an extra sixth convolutional layer over the last pooling layer, to classify the entire ImageNet Fall 2011 release (15M images, 22K categories), and then “fine-tuning” it on ILSVRC-2012 gives an error rate of 16.6%. Averaging the predictions of two CNNs that were pre-trained on the entire Fall 2011 release with the aforementioned five CNNs gives an error rate of 15.3%. The second-best contest entry achieved an error rate of 26.2% with an approach that averages the predictions of several classifiers trained on FVs computed from different types of densely-sampled features [7].
我们也以我们的模型参加了ILSVRC-2012比赛，表2中是我们的结果。由于ILSVRC-2012测试集标签不是公开的，我们不能报告我们尝试的所有模型的测试错误率。在本段接下来的部分，我们交换着使用验证错误率和测试错误率因为根据我们的经验，他们不会有超过0.1%的不同（见表2）。本文中所描述的CNN的top-5错误率是18.2%。五个相似的CNN的平均预测结果的错误率是16.4%。在最后一个池化层上增加第六个卷积层，使用整个ImageNet Fall 2011的数据（15M图像，22000种类别）作为分类数据预训练得到的一个CNN，再经过微调，用ILSVRC-2012对该CNN进行测试得到的错误率为16.6%。对上述的五个在整个Fall 2011数据集上预训练过的CNN，得到的预测求平均得到的错误率结果为15.3%。当时第二的队伍得到的错误率为26.2%，使用的方法是对基于从多种密集采样特征计算得到的FVs，训练得到多个分类器的预测值求平均[7]。

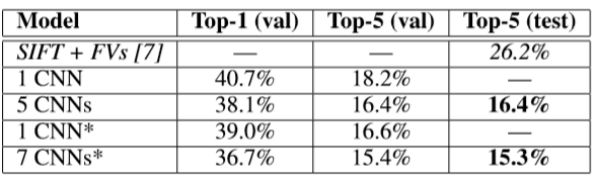
Table 2: Comparison of error rates on ILSVRC-2012 validation and test sets. In italics are best results achieved by others. Models with an asterisk* were “pre-trained” to classify the entire ImageNet 2011 Fall release. See Section 6 for details.
表2 基于ILSVRC-2012的验证集和测试集的错误率比较。斜体字是其他方法取得的最好结果。带星号*的模型预先用整个ImageNet 2011 Fall数据集训练过。详见第6节。

Finally, we also report our error rates on the Fall 2009 version of ImageNet with 10,184 categories and 8.9 million images. On this dataset we follow the convention in the literature of using half of the images for training and half for testing. Since there is no established test set, our split necessarily differs from the splits used by previous authors, but this does not affect the results appreciably. Our top-1 and top-5 error rates on this dataset are 67.4% and 40.9%, attained by the net described above but with an additional, sixth convolutional layer over the last pooling layer. The best published results on this dataset are 78.1% and 60.9% [19].
最后，我们也汇报了我们的基于包含10184钟类别890万张图像的Fall 2009的错误率。对于该数据集我们遵从文献中的约定：一半为训练集一半为测试集。由于没有确定的测试集，我们的分割必然与前面作者使用的不一样，但是这并不会明显地影响结果。我们在该数据集上得到top-1和top-5错误率分别为67.4%和40.9%，这个结果是由在上述网络的最后一个池化层加了第六层卷积层所得到的。之前在这个数据集上最好的结果是78.1%和60.9%[19]。

6.1 Qualitative Evaluations

Figure 3 shows the convolutional kernels learned by the network’s two data-connected layers. The network has learned a variety of frequency-and orientation-selective kernels, as well as various colored blobs. Notice the specialization exhibited by the two GPUs, a result of the restricted connectivity described in Section 3.5. The kernels on GPU 1 are largely color-agnostic, while the kernels on on GPU 2 are largely color-specific. This kind of specialization occurs during every run and is independent of any particular random weight initialization (modulo a renumbering of the GPUs).
图3表示由网络的两个数据连接层学习到的卷积核。该网络已经学习到了各种各样的具有频率、方向选择性的核以及多种着色斑块。注意到两个GPU展现出的特殊化，这是3.5节描述的限制连接的结果。GPU1上的核大部分颜色不可知，而GPU2上的核大部分有颜色。这种特殊化每一次运行时都会发生，并且独立于任何特定随机权值初始化（模除GPU的重编号）。

Figure 3: 96 convolutional kernels of size 11×11×3 learned by the first convolutional layer on the 224×224×3 input images. The top48 kernels were learned on GPU1 while the bottom 48 kernels were learned on GPU 2. See Section 6.1 for details.

图3 第一层卷积层对224x224x3的输入图像使用96个大小为11x11x3的卷积核学习得到的特征图。上面的48个卷积核在GPU1上学习，下面的48个卷积核在GPU2上学习。详见6.1节
In the left panel of Figure 4 we qualitatively assess what the network has learned by computing its top-5 predictions on eight test images. Notice that even off-center objects, such as the mite in the top-left, can be recognized by the net. Most of the top-5 labels appear reasonable. For example, only other types of cat are considered plausible labels for the leopard. In some cases (grille, cherry) there is genuine ambiguity about the intended focus of the photograph.
图4的左边我们通过计算8幅测试图像的top-5预测结果定性地评估了网络学习到了什么。注意到即使偏离中心的目标，例如左上方的小虫，也可以被网络识别。大多数top-5标签都显得很合理。例如，只有别的种类的猫被似是而非贴上豹子的标签。在一些情况下（窗格、樱桃）会存在对照片的意图的判断的含糊不清。

Figure 4: (Left) Eight ILSVRC-2010 test images and the five labels considered most probable by our model. The correct label is written under each image, and the probability assigned to the correct label is also shown with a red bar(if it happens to be in the top5). (Right) Five ILSVRC-2010 test images in the first column. The remaining columns show the six training images that produce feature vectors in the last hidden layer with the smallest Euclidean distance from the feature vector for the test image.
图4 （左）8幅ILSVRC-2010测试图像和五个根据本文模型得到的最可能的标签。每一幅图像下方写着正确的标签，正确标签的可能性大小也用红色条表示了出来（如果其恰巧在前5个）。（右）第一列是五幅ILSVRC-2010测试图像。剩余列表示6幅训练图像，这些训练图像在最后一层隐藏层得到的特征向量与测试图像的特征向量有最小的欧式距离。
Another way to probe the network’s visual knowledge is to consider the feature activations induced by an image at the last, 4096-dimensional hidden layer. If two images produce feature activation vectors with a small Euclidean separation, we can say that the higher levels of the neural network consider them to be similar. Figure 4 shows five images from the test set and the six images from the training set that are most similar to each of them according to this measure. Notice that at the pixel level, the retrieved training images are generally not close in L2 to the query images in the first column. For example, the retrieved dogs and elephants appear in a variety of poses. We present the results for many more test images in the supplementary material.
另一种探讨网络的视觉知识的方法就是考虑最终图像在最后4096维隐藏层产生的特征激活度。如果两幅图像产生的特征激活向量的欧氏距离很小，我们就可以说神经网络的更高层认为它们是相似的（根据了特征激活向量的欧式距离，这种测度跟视觉感官上的相似度是不同的）。图4显示了根据这种测度下的五幅测试集图像和六幅跟他们最相似的训练集图像。注意到在像素水平，第二列中检索到的训练图像一般地不会和第一列的查询图像相近。例如，检索到的狗和大象以多种姿势出现。我们在补充材料中展示更多测试图像的结果。
Computing similarity by using Euclidean distance between two 4096-dimensional, real-valued vectors is inefficient, but it could be made efficient by training an auto-encoder to compress these vectors to short binary codes. This should produce a much better image retrieval method than applying auto encoders to the raw pixels [14], which does not make use of image labels and hence has a tendency to retrieve images with similar patterns of edges, whether or not they are semantically similar.
使用欧氏距离计算4096维、实值向量之间的相似度效率较低，但是可以通过训练一个自动编码器来将这些向量压缩为短的二进制编码而提高效率。 这个相比将自动编码器直接应用到原始像素上，是一个更加好的图像检索方法[14]，前者没有利用图像的标签，因此会倾向于检索到有相似边界模式的图像，而不论他们语义上是否相似。

7 Discussion

Our results show that a large, deep convolutional neural network is capable of achieving record breaking results on a highly challenging dataset using purely supervised learning. It is notable that our network’s performance degrades if a single convolutional layer is removed. For example, removing any of the middle layers results in a loss of about 2% for the top-1 performance of the network. So the depth really is important for achieving our results.
本文的结果表明一个大规模深度卷积神经网络在具有高度挑战性的数据集上仅用监督学习就能够获得破纪录的好结果。值得注意的是如果一个卷积层被移除则本文的网络性能会降低。例如，移除任一个中间层，网络的top-1性能会降低大约2%。因此深度对本文的结果真的很重要。

To simplify our experiments, we did not use any unsupervised pre-training even though we expect that it will help, especially if we obtain enough computational power to significantly increase the size of the network without obtaining a corresponding increase in the amount of labeled data. Thus far, our results have improved as we have made our network larger and trained it longer but we still have many orders of magnitude to go in order to match the infero-temporal pathway of the human visual system. Ultimately we would like to use very large and deep convolutional nets on video sequences where the temporal structure provides very helpful information that is missing or far less obvious in static images.
为了简化本文的实验，我们没有使用任何非监督预训练即使我们认为它会起作用，尤其是我们可以在标签数据没有发生相应增长的情况下，获得足够的计算资源来增大我们网络的大小，能够有足够的计算能力去显著地增加网络的大小。迄今，由于我们使用了更大的网络，训练了更长的时间，本文的结果已经有所提高，但我们仍然有很多需求来进行时空下人类视觉系统的研究。最终我们想要将非常大规模地深度卷积网络应用于视频序列的处理，视频序列中的时间结构提供了许多有用的信息，而这些信息在静态图中丢失了或者不是很明显。

References

[1] R.M.BellandY.Koren.Lessons from the net flixprize challenge. ACM SIG KDD Explorations News letter, 9(2):75–79, 2007.
[2] A. Berg, J. Deng, and L. Fei-Fei. Large scale visual recognition challenge 2010. www.imagenet.org/challenges. 2010.
[3] L. Breiman. Random forests. Machine learning, 45(1):5–32, 2001.
[4] D. Cires¸an, U. Meier, and J. Schmidhuber. Multi-column deep neural networks for image classification. Arxiv preprint arXiv:1202.2745, 2012.
[5] D.C. Cires¸an, U. Meier, J. Masci, L.M. Gambardella, and J. Schmidhuber. High-performance neural networks for visual object classification. Arxiv preprint arXiv:1102.0183, 2011.
[6] J. Deng, W. Dong, R. Socher, L.-J. Li, K. Li, and L. Fei-Fei. ImageNet: A Large-Scale Hierarchical Image Database. In CVPR09, 2009.
[7] J. Deng, A. Berg, S. Satheesh, H. Su, A. Khosla, and L. Fei-Fei. ILSVRC-2012, 2012. URL http://www.image-net.org/challenges/LSVRC/2012/.
[8] L. Fei-Fei, R. Fergus, and P. Perona. Learning generative visual models from few training examples: An incremental bayesi an approach tested on 101 object categories. Computer Vision and Image Understanding, 106(1):59–70, 2007.
[9] G. Griffin, A. Holub, and P. Perona. Caltech-256 object category dataset. Technical Report 7694, California Institute of Technology, 2007. URL http://authors.library.caltech.edu/7694.
[10] G.E. Hinton, N. Srivastava, A. Krizhevsky, I. Sutskever, and R.R. Salakhutdinov. Improving neural networks by preventing co-adaptation of feature detectors. arXiv preprint arXiv:1207.0580, 2012.
[11] K. Jarrett, K. Kavukcuoglu, M. A. Ranzato, and Y. LeCun. What is the best multi-stage architecture for object recognition? In International Conference on Computer Vision, pages 2146–2153. IEEE, 2009.
[12] A. Krizhevsky. Learning multiple layers of features from tiny images. Master’s thesis, Department of Computer Science, University of Toronto, 2009.
[13] A. Krizhevsky. Convolutional deep belief networks on cifar-10. Unpublished manuscript, 2010.
[14] A. Krizhevsky and G.E. Hinton. Using very deep autoencoders for content-based image retrieval. In ESANN, 2011.
[15] Y. Le Cun, B. Boser, J.S. Denker, D. Henderson, R.E. Howard, W. Hubbard, L.D. Jackel, et al. Hand written digit recognition with a back-propagation network. In Advances in neural information processing systems, 1990.
[16] Y. LeCun, F.J. Huang, and L. Bottou. Learning methods for generic object recognition with invariance to pose and lighting. In Computer Vision and Pattern Recognition, 2004. CVPR 2004. Proceedings of the 2004 IEEE Computer Society Conference on, volume 2, pages II–97. IEEE, 2004.
[17] Y. LeCun, K. Kavukcuoglu, and C. Farabet. Convolutional networks and applications in vision. In Circuits and Systems (ISCAS), Proceedings of 2010 IEEE International Symposium on, pages 253–256. IEEE, 2010.
[18] H. Lee, R. Grosse, R. Ranganath, and A.Y. Ng. Convolutional deep belief networks for scalable unsupervised learning of hier archical representations. In Proceedings of the 26th Annual International Conference on Machine Learning, pages 609–616. ACM, 2009.
[19] T. Mensink, J. Verbeek, F. Perronnin, and G. Csurka. Metric Learning for Large Scale Image Classification: Generalizing to New Classes at Near-Zero Cost. In ECCV - European Conference on Computer Vision, Florence, Italy, October 2012.
[20] V. Nair and G. E. Hinton. Rectified linear units improve restricted boltzmann machines. In Proc. 27th International Conference on Machine Learning, 2010.
[21] N. Pinto, D.D. Cox, and J.J. DiCarlo. Why is real-world visual object recognition hard? PLoS computational biology, 4(1):e27, 2008.
[22] N. Pinto, D. Doukhan, J.J. DiCarlo, and D.D. Cox. A high-throughput screening approach to discovering good forms of biologically inspired visual representation. PLoS computational biology, 5(11):e1000579, 2009.
[23] B.C. Russell, A. Torralba, K.P. Murphy, and W.T. Freeman. Labelme: a database and web-based tool for image annotation. International journal of computer vision, 77(1):157–173, 2008.
[24] J.SánchezandF.Perronnin. High-dimensionalsignaturecompressionforlarge-scaleimageclassification. InComputerVisionandPatternRecognition(CVPR),2011IEEEConferenceon,pages1665–1672.IEEE, 2011.
[25] P.Y. Simard, D. Steinkraus, and J.C. Platt. Best practices for convolutional neural networks applied to visualdocumentanalysis. InProceedingsoftheSeventhInternationalConferenceonDocumentAnalysis and Recognition, volume 2, pages 958–962, 2003.
[26] S.C.Turaga,J.F.Murray,V.Jain,F.Roth,M.Helmstaedter,K.Briggman,W.Denk,andH.S.Seung. Convolutional networks can learn to generate affinity graphs for image segmentation. Neural Computation, 22(2):511–538, 2010.