GNU Octave计算数据
GNU Octave计算数据
矩阵的乘法运算
为了便于计算,我们初始化几个矩阵变量,比如设置A为一个3x2的矩阵,设置B为一个3x2的矩阵,设置C为2x2的矩阵。
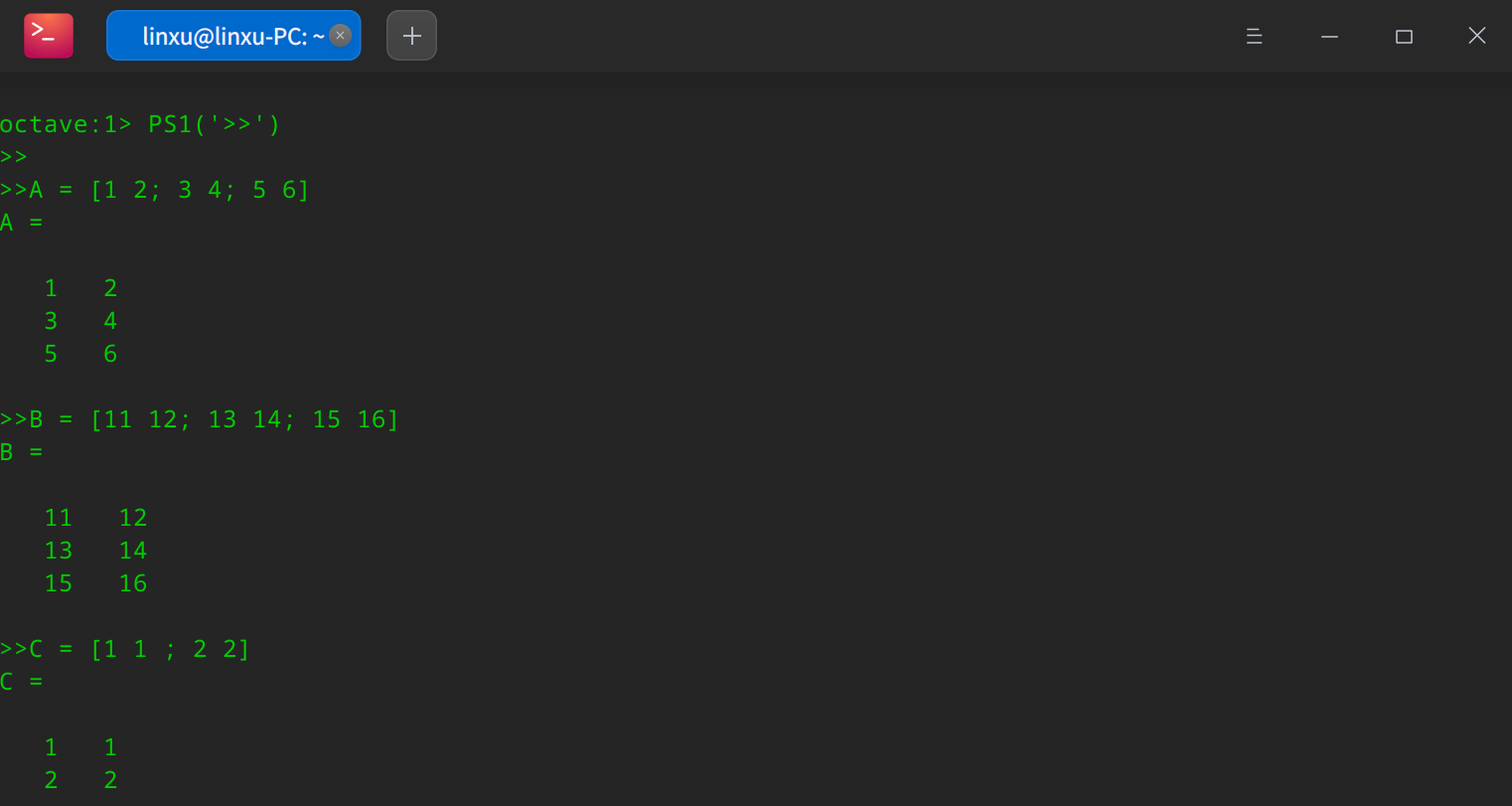
这时要算两个矩阵的乘积,比如说AxC,只需要输入AxC,也就是将一个3x2的矩阵乘以2x2的矩阵,那么就可以得到一个3x2的矩阵。

矩阵的点-乘运算
同时你也可以对每个元素做点乘运算,命令是A.*B,得到的结果是A中的每个元素与矩阵B中的对应元素相乘。
我们可以推演一下,这里的第一个元素1乘以11得到11,第二个元素2乘以12得到24,这就是两个矩阵的元素位运算。
通常来说,在Octave中"."(点号)一般用来表示元素位运算。

矩阵的点-次方运算
类似地,我们可以输入A.^2,这将对矩阵A中每个元素进行平方

矩阵的点-除运算
同样,我们设V为[1;2;3]为一维列向量,那么你可以输入1./V,就可以得到对应的每个元素的导数,这样一来就会分别算出1/1,1/2, 1/3。

同样,矩阵也有类似的操作,1./A就可以得到A中每个元素的倒数。

矩阵的点-对数运算
进一步推广,我们还可以对矩阵中的每个元素进行求对数运算。

矩阵的点-幂次运算
还可以自然对数e进行幂次运算,也就是以e为底,以这些元素为幂的运算。

取相反数
同时,可以对V进行求每个元素的相反数

求绝对值
此外,还可以使用abs来对列向量V的每个元素求绝对值

矩阵同+某个元素

另一种更简单的方法是直接用v+1,v+1也就等于把v中的每个元素都加上1.

矩阵的转置
对于矩阵A,如果你想要求它的转置,那么方法是用A'进行计算,这将返回对于A的转置矩阵。
特殊地,如果对同一个矩阵A进行转置两次,也就是(A')',那么就会重新得到原矩阵A。

求最值
或许我们还需要求一个集合中的最值,比如:a = [1 15 20 0.5],这是1行4列矩阵,val=max(a)将会返回a矩阵中的最大值15。

同样,val=min(a)将会返回a矩阵中的最小值0.5.

求元素索引
我们还可以通过[val, ind] = max(a),这将使得A矩阵中的最大值存入val,并且将该值对应的索引,元素对应的索引值为2,存入ind,所以ind=2。

特别需要注意的是,如果你用命令max(A),而A是一个矩阵的话,这样做就是对每一列求最大值。

矩阵元素判断
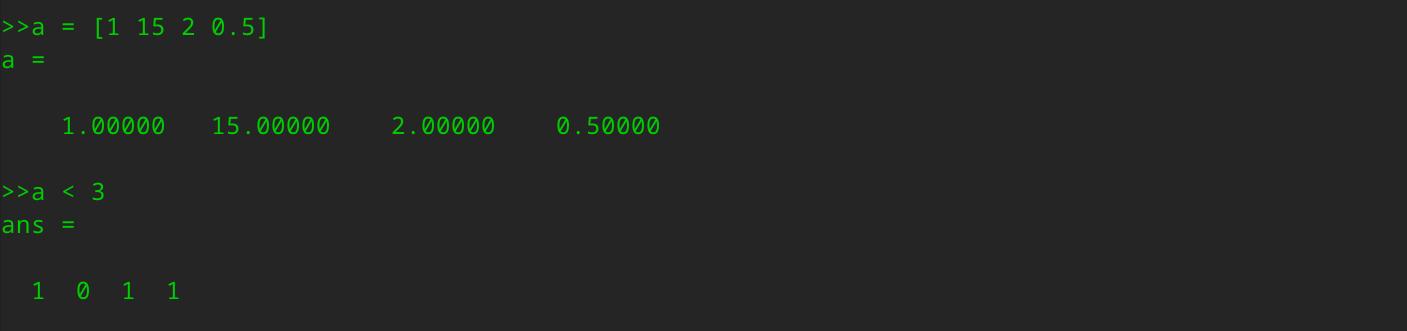
我们还是用这个例子,若a矩阵a=[1 15 2 0.5],那么那么输入a<3,这将进行逐元素的运算,所以矩阵中元素小于3的返回1,否则返回0。
因此会得到[1 1 0 1]的结果,也就是说,对a矩阵a=[1 15 2 0.5],如果输入a<3,这将进行逐元素的运算,所以元素小于3的返回1,否则返回0。
矩阵元素查找
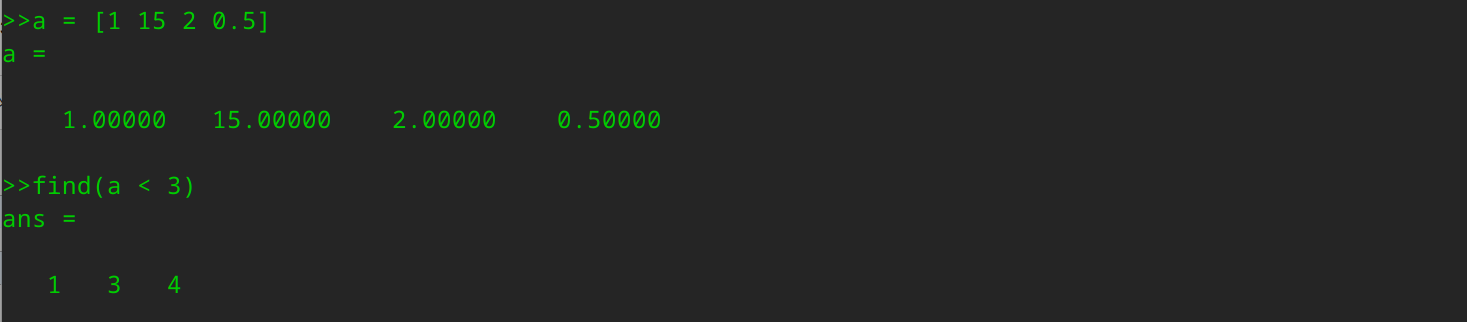
对于矩阵a,如果你写find(a<3),这将输出a中那些小于3的元素索引值(注意:octave中的索引是以1开始的)。
更复杂一些的用法是,如果输入[r,c] = find(a>=7),这将找出所有a矩阵中大于等于7的元素,因此,r和c分别表示行和列,这就表示,第1行第1列的元素大于等于7,第3行第2列的元素大于等于7,第2行第3列的元素大于等于7。

顺便说一句,其实没有必要去刻意记住这个find函数的用法,只需要会用help函数就行了,每当在使用这个函数忘记怎么用的时候,就可以用help函数,使用help find来找到帮助文档。
魔方阵/幻方
设A=magic(3),magic函数将返回一个矩阵,该矩阵称为魔方阵或幻方(magic squares),它们具有以下这样的数学性质:它们所有的行和列和对角线加起来都等于相同的值。

元素求和
除此之外,或许你还需要对矩阵a中的元素进行求和,那么就可以使用sum函数
这时输入sum(a),就可以把a中的所有元素加起来了。

元素连乘
如果你想要将矩阵中的元素都乘起来,那么可以输入prod(a),prod函数是意思是product(乘积),他将返回矩阵a中各元素的乘积。

元素舍入
我们还可以对元素进行向上向下的四舍五入。
其中floor(a)是向下四舍五入,因此对于a中的元素0.5将被下舍入变成0.

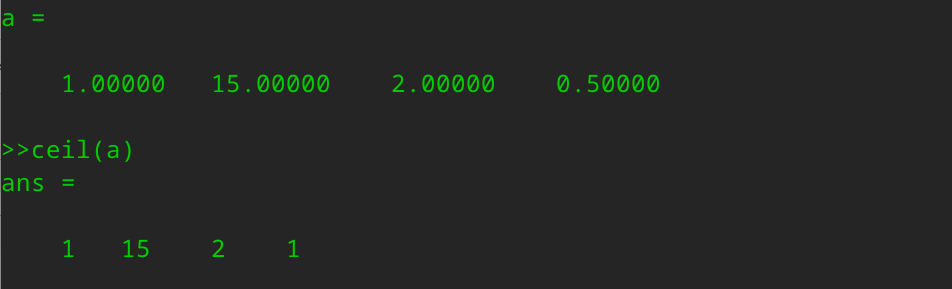
另外ceila(a)表示向上四舍五入,所以0.5将上舍入变为最接近的整数,也就是1.
一些复杂操作
如果输入max(rand(3), rand(3)),这将返回两个3x3的随机矩阵,并且逐元素比较取最大值。

假如输入max(A,[],1),这样做会得到每一列的最大值,这里第一例的最大值就是8,第二列是9,第三列的最大值是7,[]后面的1表示取A矩阵的第一个维度的最大值。

相对地,如果键入max(A,[],2),这将得到每一行的最大值,所以第一行的最大值是等于8,第二行最大值是7,第三行是9。
所以你可以用这个方法来求得每一行或每一列的最值,另外,主要注意的是,默认情况下max(A)返回的是每一列的最大值,如果你想要找出整个矩阵A的最大值,你可以输入max(max(A)),或者你可以将A矩阵转成一个向量,然后输入max(max(A)),或者你可以将A矩阵转成一个向量,然后键入max(A(😃),这样做的意义就是把A当做一个向量,并返回A向量中的最大值。

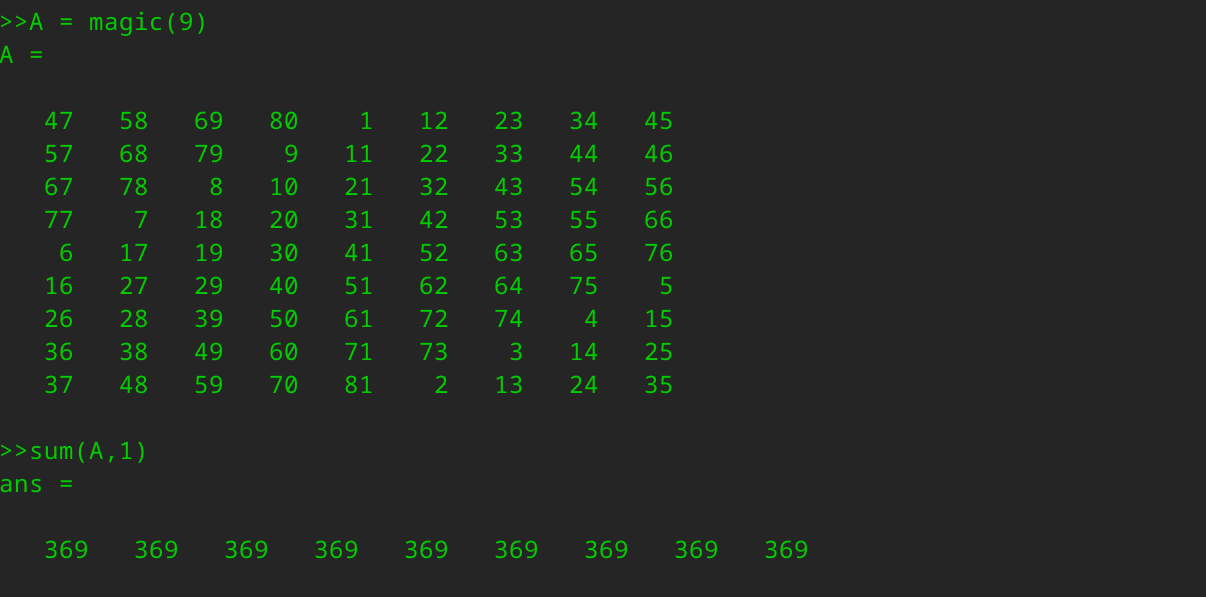
最后,让我们把A设为一个9行9列的魔方阵,魔方阵具有的特性是每行每列和对角线的求和都是相等的。
下面这是一个9X9的魔方阵,我们来求一个sum(A,1),这样就得到每一列的综合,这也验证了一个9x9的魔方阵确实每一列加起来都相等,都为369。
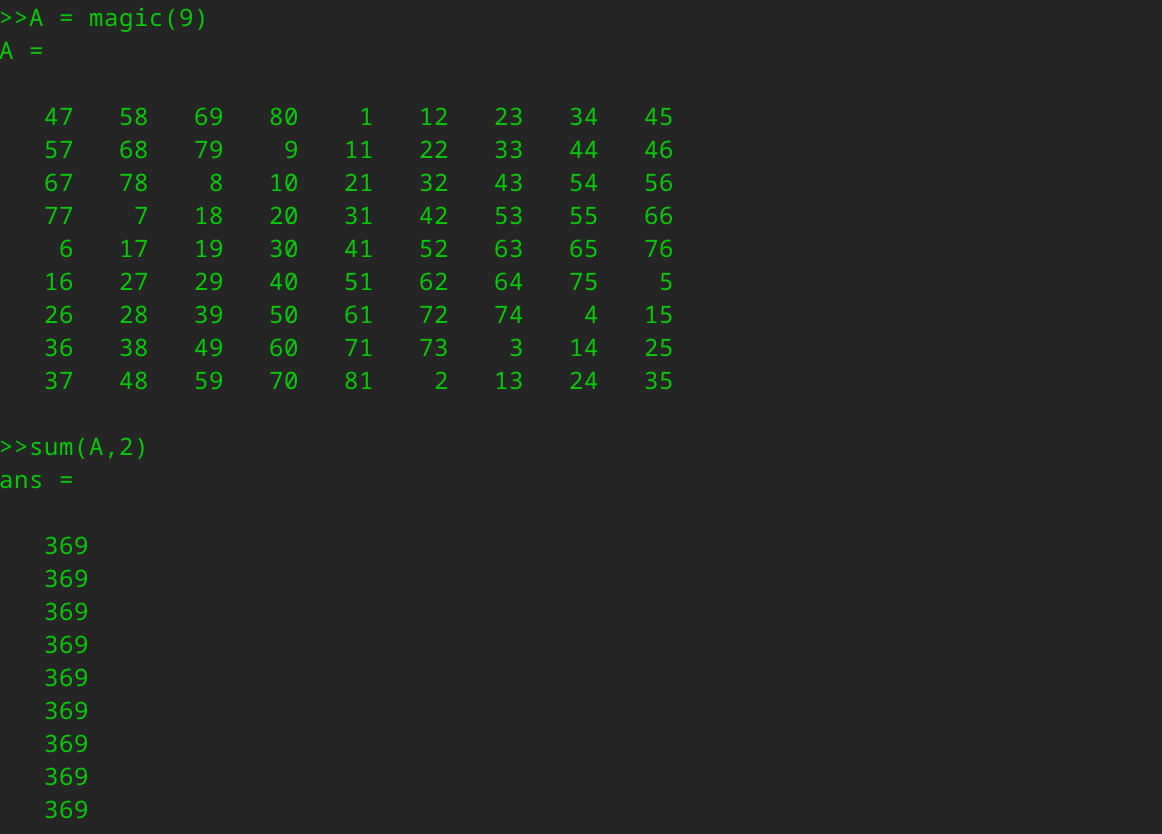
现在我们来求每一行的和,可以输入sum(A,2),这样就得到了A中每一行加起来都是369。
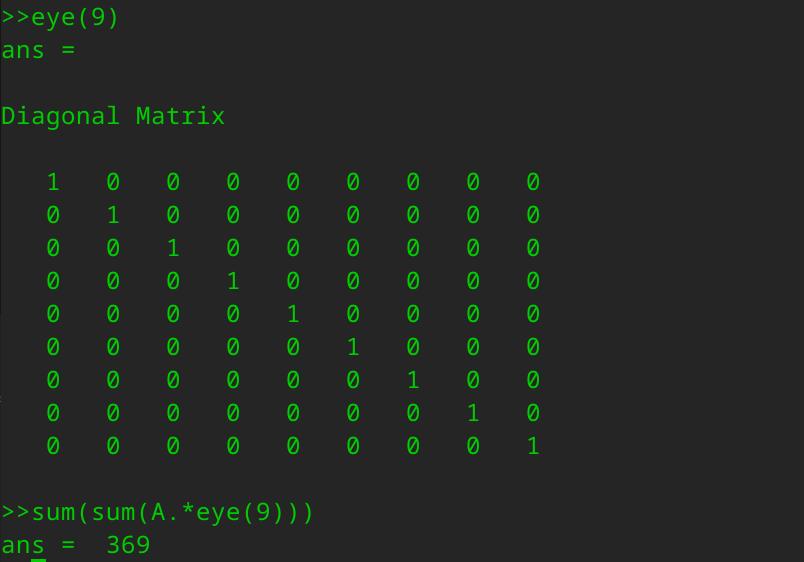
现在我们来算A的对角线元素的和。
先来构造一个9x9的单位矩阵,输入eyes(9),然后我们要用A逐点乘以这个单位矩阵,除了对角线元素外,其他元素都会得到0.
然后输入sum(sum(A,*eye(9))),这实际上是求得了,这个矩阵对角线元素的和确实是369.
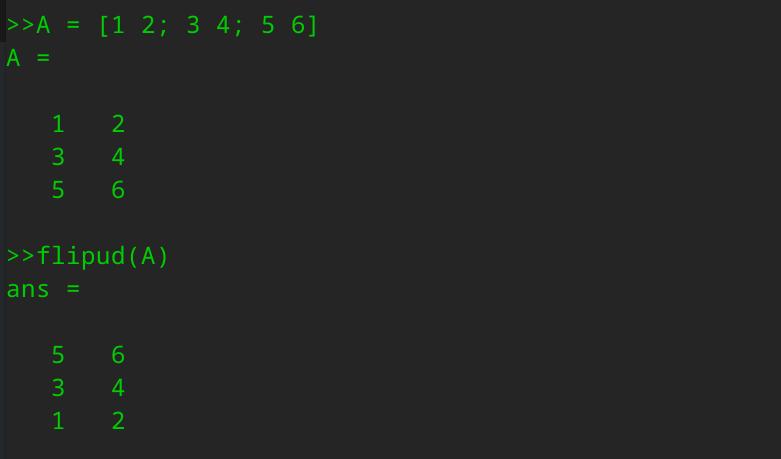
矩阵翻转
flipup/flipud表示向上/向下翻转
矩阵求逆
想要求pinv(A),通常称为伪逆矩阵,你就把它看成矩阵A求逆,因此这就是A矩阵的逆矩阵。

设temp = pinv(A),然后再用temp乘以A,这实际上得到就是单位矩阵,对角线为1,其他元素为0.



 浙公网安备 33010602011771号
浙公网安备 33010602011771号