机器学习-集成学习

(一)集成学习的基本概念
(二)Boosting
(三)随机森林
(四)结合策略
(五)多样性
(六)梯度相关
这里考纲只要求(一)至(三)。

(零) 前置知识

0 基础概念

0.1 伯努利实验

伯努利试验（Bernoulli trial）(或译为白努利试验)是只有两种可能结果（成功或失败）的单次随机试验，即对于一个随机变量X而言，

\[P_r[X=1] = p \\ P_r[X=0] = 1-p \]

在数学上，这样的试验是以随机变量为模型，而随机变量只能有两个值：0和1，1被认为是"成功"。在单次的伯努利试验中，如果 p 是成功的概率，那么将呈现伯努利分布，此时随机变量的期望值就是 p ，且其标准差$\sqrt{p(1-p)}$。

一个伯努利过程（Bernoulli process）是由重复出现独立但是相同分布的伯努利试验组成，例如抛硬币十次，而此时呈现之结果将呈现二项分布。

0.2 $Hodffding$(霍夫丁不等式)

　　霍夫丁不等式（Hoeffding's inequality）是机器学习的基础理论，通过它可以推导出机器学习在理论上的可行性。霍夫丁不等式经常被应用于一些独立分布的伯努利随机变量的重要特例中，这也是为什么这个不等式在计算机科学以及组合数学中如此常见。

0.2.1 伯努利随机变量的特例

我们认为一个抛硬币时一个硬币A面朝上的概率为$p$，B面朝上的概率则为$1-p$。我们抛$n$次硬币，那么A面朝上次数的期望值为$np$。那么进一步我们可以知道，A面朝上的次数不超过k次的概率能够被下面的表达式完全确定：

\[\mathbb{P}(H(n)\leq k) = \sum \limits_{i=0}^k \begin{pmatrix} n \\i\end{pmatrix}p^i(1-p)^{n-i} \]

这里的$H(n)$为抛n次硬币其Ａ面朝上的次数。
对于某一$\varepsilon>0$，当$k=(p-\varepsilon)n$时，上面不等式确定的霍夫丁上界将会按照指数级变化：

\[\mathbb{P(H(n)} \leq (p-\varepsilon)n) \leq exp(-2\varepsilon^2n) \]

相似的，对于某一$\varepsilon>0$，当$k=(p+\varepsilon)n$，霍夫丁不等式的概率边界同样可以确定为:

\[\mathbb{P}(H(x) \geq (p+\varepsilon)n)　\leq exp(-2 \varepsilon^2n) \]

这样根据上面两个式子我们可以得到：

\[\mathbb{P}((p-\varepsilon)n \leq H(n) \leq (p+\varepsilon)n) \geq 1-2exp(-2\varepsilon^2n) \]

比如说现在我们令$\varepsilon = \sqrt{\frac{ln n}{n}}$，那么可以得到

\[\mathbb{P}(|H(n) - pn|\leq\sqrt{nlnn}) \geq 1-2exp(-2ln2) = 1 - \frac{2}{n^2} \]

0.2.2 伯努利的普遍情况

现在令$X_1,X_2,...,X_n$为[0,1]的独立随机变量，即$0\leq X_i \leq 1$。
我们定义这些变量的经验均值为:

\[\overline{X} = \frac{1}{(X_1+X_2+...+X_n)} \]

在1963年霍夫丁提出该不等式，其中霍夫丁定理一中的一个不等式为：

\[\mathbb{P}(\overline{X}-E[\overline{X}] \geq t) \leq e^{-2nt^2} \]

当知道$X_i$严格的边界范围$a_i,b_i$(即$X_i$属于[$a_i,b_i$])时，霍夫丁定理二更加广泛：

\[\mathbb{P}(\overline{X}-E[\overline{X}] \geq t) \leq exp \left(-\frac{2n^2t^2}{\sum \limits_{i=1}^n(b_i-a_i)^2 }\right) \\ \mathbb{P}(\overline{X}-E[\overline{X}] \geq t) \leq 2exp \left(-\frac{2n^2t^2}{\sum \limits_{i=1}^n(b_i-a_i)^2 }\right) \]

其中$S_n = X_1 + X_2 +...+X_n$.

0.3 决策树

0.3.1 决策树简介

在解释随机森林前，需要先提一下决策树。决策树是一种很简单的算法，他的解释性强，也符合人类的直观思维。这是一种基于if-then-else规则的有监督学习算法。

　　机器学习中，决策树是一个预测模型；他代表的是对象属性与对象值之间的一种映射关系。树中每个节点表示某个对象，而每个分叉路径则代表某个可能的属性值，而每个叶节点则对应从根节点到该叶节点所经历的路径所表示的对象的值。决策树仅有单一输出，若欲有复数输出，可以建立独立的决策树以处理不同输出。数据挖掘中决策树是一种经常要用到的技术，可以用于分析数据，同样也可以用来作预测。

　　从数据产生决策树的机器学习技术叫做决策树学习,通俗说就是决策树。　

一个决策树包含三种类型的节点：

1.决策节点：通常用矩形框来表示
2.机会节点：通常用圆圈来表示
3.终结点：通常用三角形来表示

　　决策树学习也是数据挖掘中一个普通的方法。在这里，每个决策树都表述了一种树型结构，它由它的分支来对该类型的对象依靠属性进行分类。每个决策树可以依靠对源数据库的分割进行数据测试。这个过程可以递归式的对树进行修剪。当不能再进行分割或一个单独的类可以被应用于某一分支时，递归过程就完成了。另外，随机森林分类器将许多决策树结合起来以提升分类的正确率。

0.3.2 决策树类型

决策树有几种产生方法：

分类树分析是当预计结果可能为离散类型（例如三个种类的花，输赢等）使用的概念。
回归树分析是当局域结果可能为实数（例如房价，患者住院时间等）使用的概念。
CART分析是结合了上述二者的一个概念。CART是Classification And Regression Trees的缩写.
CHAID（Chi-Square Automatic Interaction Detector）

0.3.3 决策树的优点

相对于其他数据挖掘算法，决策树在以下几个方面拥有优势：

决策树易于理解和实现.人们在通过解释后都有能力去理解决策树所表达的意义。
对于决策树，数据的准备往往是简单或者是不必要的.其他的技术往往要求先把数据一般化，比如去掉多余的或者空白的属性。
能够同时处理数据型和常规型属性。其他的技术往往要求数据属性的单一。
是一个白盒模型如果给定一个观察的模型，那么根据所产生的决策树很容易推出相应的逻辑表达式。
易于通过静态测试来对模型进行评测。表示有可能测量该模型的可信度。
在相对短的时间内能够对大型数据源做出可行且效果良好的结果。

0.3.4 决策树的缺点

对于那些各类别样本数量不一致的数据，在决策树当中信息增益的结果偏向于那些具有更多数值的特征。

(一) 集成学习的基本概念

1.0 什么是集成学习?

　集成学习归属于机器学习，它是一种「训练思路」，并不是某种具体的方法或者算法。

　现实生活中，大家都知道「人多力量大」，「3 个臭皮匠顶个诸葛亮」。而集成学习的核心思路就是「人多力量大」，它并没有创造出新的算法，而是把已有的算法进行结合，从而得到更好的效果。

集成学习会挑选一些简单的基础模型进行组装，组装这些基础模型的思路主要有 2 种方法：

bagging（bootstrap aggregating的缩写，也称作“套袋法”）
boosting

1.1 概述

　　监督学习算法通常被描述为执行搜索假设空间的任务以找到合适的假设，该假设将对特定问题做出良好的预测。即使假设空间包含非常适合特定问题的假设，也可能很难找到一个很好的假设。集成学习结合多个假设，形成一个(希望)更好的假设。评估集成学习的预测通常需要比评估单个模型的预测更多的计算，因此集成可以被认为是通过执行大量额外计算来补偿差的学习算法的方式。诸如决策树之类的快速算法通常用于集合方法(如随机森林)，尽管较慢的算法也可以从集成方法中受益。

通过类比，集成技术也已用于无监督学习场景中，如共识聚类或异常检测。

1.2 集成理论

　　集成学习本身是一种监督学习算法，因为它可以被训练然后用于进行预测。因此，训练后的集成模型代表了一个假设，但这个假设不一定被包含在构建它的模型的假设空间内。因此，可以正面集成学习在它们可以表示的功能方面具有更大的灵活性，理论上，这种灵活性使他们能够比单一模型更多地过拟合训练数据，但在实践中，一些集成算法(如Bagging算法)倾向于减少对训练数据过拟合相关的问题。
　　根据经验，当模型之间存在显著差异时，集成往往会产生更好的结果。因此，许多集成方法试图促进它们组合的模型之间的多样性。尽管可能不是直观的，更随机的算法(如随机决策树)可用于产生比非常有意识的算法(如熵减少决策树)更强大的集成模型。然而，使用各种强大的学习算法已被证明是比使用试图愚弄模型以促进多样性的技术更有效。

1.3 集成模型大小

虽然集成中的组成分类器的数量对预测的准确性具有很大影响，但是解决该问题的研究数量比较有限。先验地确定集成模型的大小以及大数据流的体积和速度使得这对于在线集成分类器来说更加重要，其中大多数统计测试被用于确定适当数量的组件。最近，理论框架表明对于集成模型存在理想数量的分类器，具有多于或少于该数量的分类器将使精度变差，这被称为“集成构建效果递减规律”。理论框架表明，使用与类标签数相同的独立分类器可以达到最高的准确率。

1.4 个体与集成

　　集成学习(ensemble learning)通过构建并集合多个学习器来完成学习任务，有时也被称为多分类器系统(multi-classifier system)、基于委员会的学习(committee-based learning)等。
　　
　　集成学习的一般结构：先产生一组“个体学习器”(individual learner)，再用某种策略将它们结合起来。

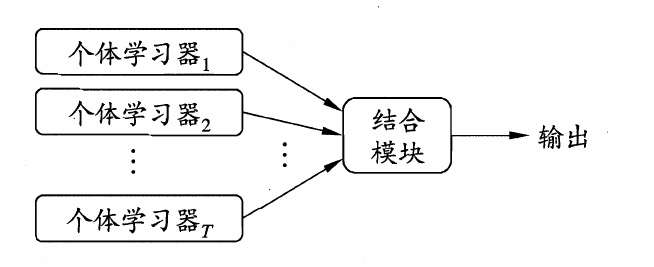
个体学习器通常由一个线程的学习算法从训练数据产生，例如$C4.5$决策树算法、BP神经网络算法等。

此时集成中只包含同种类型的个体学习器，例如“决策树集成”中全是决策树，“神经网络集成”中全是神经网络，这样的集成是“同质”的(homogeneous)。

同质集成：同质集成中的个体学习器称为“基学习器”（base learner），相应的学习算法为“基学习算法”（base learning algorithm）。

集成也可包含不同类型的个体学习器，例如同时包含决策树和神经网络，这样的集成是“异质的”。

异质集成：异质集成中的个体学习器由不同的学习算法生成，称为“组件学习器”（component learner）或直称为“个体学习器”。

　　同质集成中的个体学习器亦称为“基学习器”(base learner)，相应的学习算法称为“基学习算法”(base learning algorithm)。集成也可包含不同类型的个体学习器，例如同时包含决策树和神经网络，这样的集成是“异质”的(heterogenous)。
　　异质集成中的个体学习器由不同的学习算法生成，这时就不再由基学习算法；相应的，个体学习器一般不称为基学习器，常称为“组件学习器”(component learner)或直接称为个体学习器。

　　集成学习通过将多个学习器进行结合，常可获得比单一学习器显著优越的泛化性能。这对“弱学习器”(weak learner)尤为明显，因此集成学习的很多理论研究都是针对弱学习器进行的，而基学习器有时也被直接称为弱学习器。但需注意的是，虽然从理论上来说使用弱学习器集成足以获得好的性能，但在实践中出于种种考虑，例如希望使用较少的个体学习器，或是重用关于常见学习器的一些经验等，人们往往会使用比较强的学习器。

　考虑一个简单的例子：在二分类任务中，假定三个分类器($h_1,h_2,h_3$)在三个测试样本上的表现如下图所示，

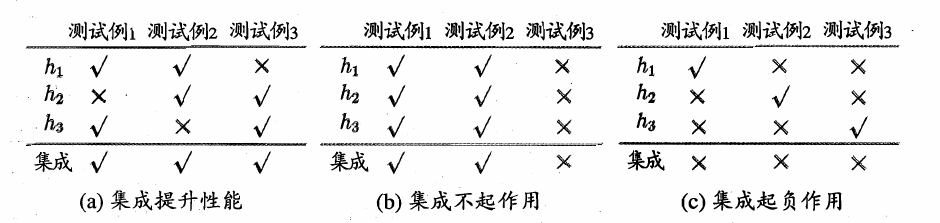
其中$“√”$表示分类正确，“×”表示分类错误，集成学习的结果通过投票法(voting)产生，即“少数服从多数”。

　　在下图(a)中，每个分类器($h_1,h_2,h_3$)都只有$66.6%$的精度，但集成学习却达到了$100$%；

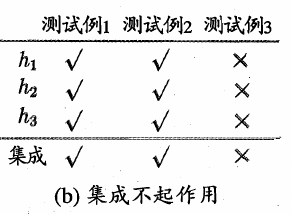
　　在下图(b)中，三个分类器没有差别，集成之后性能没有提高；

　　在下图(c)中，每个分类器的精度都只有$33.3$％，集成学习的结果变得更糟。　　　

　　以上这个简单的例子显示出：要获得好的集成，个体学习器应“好而不同”，即个体学习器要有一定的“准确性”，即学习器不能太坏，并且要有“多样性”(diversity)，即学习器间具有差异。
　　
　　我们来做个简单的分析。考虑二分类问题$y∈\left\{-1,+1\right\}$和真实函数$f$，假定基分类器之间相互独立（能提供较高的差异度），且错误率相等为$\epsilon$，即对每个基分类器$h_i$有

\[P(h_i(x)\neq f(x)) = \epsilon \quad \quad (8.1) \]

注意到$f(x)$为x的真实标记，而$h_i(x)$为基分类器$h_i$对$x$的预测标记，因此$h_i(x)\neq f(x)$表示预测标记与真实标记不相同的情况，即预测出错，$P(h_i(x)\neq　f(x))$即为错误率

　假设集成通过简单投票法结合$T$个基分类器，若有超过半数的基分类器正确，则集成分类就正确;

\[H(x) = sign \left(\sum \limits_{i=1}^T h_i(x) \right) \quad \quad (8.2) \]

注意到当前仅针对二分类问题$y∈\left\{-1,+1\right\}$，即预测标记$h_i(x)∈ \left\{-1,+1\right\}$。因此，若$T$个基分类器中预测输出+1占半数以上，则$\sum \limits_{i=1}^Th_i(x)>0$；反之，若$T$个基分类器中预测输出-1占半数以上，则$\sum \limits_{i=1}^Th_i(x)<0$。函数$sign(\cdot)$为符号函数，在$\cdot<0$时取值为-1，在$\cdot>0$时取值为+1，即函数$H(x)$与多数基分类器输出一致，即满足多数投票，少数服从多数。

　假设基分类器的错误率相互独立，则由$Hodffding$(霍夫丁)不等式可知，集成的错误率为

\[P(H(x)\neq f(x)) = \sum \limits_{k=1}^{\lfloor T/2 \rfloor}\begin{pmatrix} T \\k\end{pmatrix}(1-\epsilon)^k \epsilon^{T-k} \\ \leq exp \left(-\frac{1}{2}T(1-2\epsilon)^2 \right) \quad \quad (8.3) \]

式(8.3)的推导

本节推导基于Hoeffding不等式。首先将本章课后习题8.1的式(8.43)变形如下：
　　　$P(H(T) \leq　\lfloor T/2 \rfloor) = \sum \limits_{k=1}^{\lfloor T/2 \rfloor}\begin{pmatrix} T \\k\end{pmatrix}(1 - \epsilon)^k \epsilon^{T-k}$
从式(8.43)到上式的符号变化包括$n \to T, k \to \lfloor T/2\rfloor, i \to k, p \to (1 - \epsilon)$。相应的，对应接下来的式(8.44),则对$\delta>0, \lfloor T/2 \rfloor = (1 - \epsilon - \delta)T$，有Hodeffding不等式
　　$P(H|T) \leq (1 - \epsilon - \delta)T = e^{-2\delta^2 T}$
对于$\lfloor T / 2\rfloor = (1 - \epsilon - \delta)T$，整理变形得$\delta$表达式
　　　$\delta = 1 - \epsilon - \frac{\lfloor T /2 \rfloor}{T}$
注意到集成学习要求基分类器泛化性能优于随机猜测的学习器，例如在二分类问题上精度略高于50%的分类器，即$\epsilon < 0.5$，因此$1 - \epsilon > \frac{1}{2}$；而$\frac{\lfloor T / 2\rfloor}{T} \leq \frac{1}{2}$(符号$\lfloor \cdot \rfloor$表示向下取整，“＝”在$T$为偶数时成立，若$T$为奇数，则一定是“<”)。因此
　　$P(H(T) \leq \lfloor T / 2\rfloor) = e^{-2\delta^2T} \leq e^{-2(1 - \epsilon - \frac{1}{2})^2T} = e^{-\frac{T}{2}(1 - 2\epsilon)^2}$
而根据式(8.2)中$H(x)$的含义，$H(T) \leq \lfloor T / 2\rfloor$(即$T$个基分类器中预测正确的个数不超过$\lfloor T /2\rfloor$，也就是预测错误)与$H(x) \neq f(x)$等价，至此，本式推导完毕。

上式显示出，随着集成中个体分类器数目Ｔ的增大，集成的错误率将指数级下降，最终趋向于零。

　　然而我们必须注意到，上面的分析有一个关键假设：基学习器的误差相互独立。在现实任务中，个体学习器是为解决同一个问题训练出来的，它们显然不可能相互独立!事实上，个体学习器的“准确性”和“多样性”本身就存在冲突。一般的，准确性很高之后，要增加多样性就需要牺牲准确性。事实上，如何产生并结合“好而不同”的个体学习器，恰是集成学习研究的核心。
　　
　　根据个体学习器的生成方式，目前的集成学习方法大致可分为两大类，即个体学习器间存在强依赖关系、必须串行生成的序列化方法，以及个体学习器间不存在强依赖关系、可同时生成的并行化方法；前者的代表是$Boosting$，后者的代表是$Bagging$和“随机森林”(Random Forest)

(二) Boosting 提升方法

　　提升(Boosting)方法是一种常用的统计学习方法，应用广泛且有效。在分类问题中，它通过改变训练样本的权重，学习多个分类器，并将这些分类器进行线性组合，提高分类的性能。

　　Boosting是一族可将弱学习器提升为强学习器的算法。这族算法的工作机制类似：
先从初始训练集训练出一个基学习器，再根据基学习器的表现对训练样本分布进行调整，使得先前基学习器做错的训练样本在后续受到更多关注，然后基于调整后的样本分布来训练下一个基学习器；如此重复进行，直至基学习器数目达到事先指定的值Ｔ，最终将这Ｔ个基学习器进行加权结合。

　　Boosting是一种串行的工作机制，即个体学习器的训练存在依赖关系，必须一步一步序列化进行。其基本思想是：增加前一个基学习器在训练训练过程中预测错误样本的权重，使得后续基学习器更加关注这些打标错误的训练样本，尽可能纠正这些错误，一直向下串行直至产生需要的$T$个基学习器，Boosting最终对这$T$个学习器进行加权结合，产生学习器委员会。

2.0 提升方法的基本思路

　　提升方法基于这样一种思想：对于一个复杂任务来说，将多个专家的判断进行适当的综合所得出的判断，要比其中任何一个专家单独的判断好。实际上，这就是说“三个臭皮匠顶个诸葛亮”的道理。
　　历史上，Kearns和Valiant首先提出了“强可学习(strongly learnable)”和“弱可学习(weakly learnable)”的概念。指出：在概率近似正确(probably approximately correct,PAC)学习的框架中，一个概念(一个类)，如果存在一个多项式的学习算法能够学习它，并且正确率很高，那么就称这个概念是强可学习的；一个概念。如果存在一个多现实的学习算法能够学习它，学习的正确率仅比随机猜测略好，那么就称这个概念是弱可学习的。非常有趣的是Schapire后来证明强可学习与弱可学习是等价的，也就是说，在PAC学习的框架下，一个概念是强可学习的充分必要条件是这个概念是弱可学习的。
　　这样一来，问题便称为，在学习中，如果已经发现了“弱学习算法”，那么能否将它提升(boost)为“强学习算法”。大家知道，发现弱学习算法通常要比发现强学习算法容易得多。那么如何具体实施提升，便成为开发提升方法时所要解决的问题。关于提升方法的研究有很多，有很多算法被提出。最具代表性的是AdaBoost算法(AdaBoost algorithm)。
　　对于分类问题而言，给定一个训练样本集，求比较粗糙的分类规则(弱分类器)要比求精确的分类规则(强分类器)容易得多。提升方法就是从弱学习算法出发，反复学习，得到一系列弱分类器(又称为基本分类器)，然后组合这些分类器，构成一个强分类器。大多数的提升方法都是改变训练数据的概率分布(训练数据的权值分布)，针对不同的训练数据分布调用一系列弱分类器。

这样，对提升方法来说，有两个问题需要回答：

一是在每一轮如何改变训练数据的权值或概率分布；
二是如何将弱分类器组合成一个强分类器。

　　关于第一个问题的，AdaBoost的做法是，提高那些被前一轮弱分类器错误分类样本的权值，而降低那些被正确分类样本的权值。这样一来，那些没有得到正确分类的数据，由于其权值的加大而受到后一轮的弱分类器的更大关注。于是，分类问题被一系列的弱分类器“分而治之”。
　　至于第二个问题，即弱分类器的组合，AdaBoost采取加权多数表决的方法。具体地，加大分类误差率小的弱分类器的权值，使其在表决中起到较大的作用，减小分类误差率大的弱分类器的权值，使其在表决中起较小的作用。
　　AdaBoost的巧妙之处就在于它将这些想法自然且有效地实现在一种算法里。

2.1 AdaBoost算法

Boosting族算法最著名、使用最为广泛的就是AdaBoost，因此下面主要是对AdaBoost算法进行介绍。AdaBoost使用的是指数损失函数，因此AdaBoost的权值与样本分布的更新都是围绕着最小化指数损失函数进行的。
看到这里回想一下之前的机器学习算法，不难发现机器学习的大部分带参模型只是改变了最优化目标中的损失函数：

如果损失函数是Square Loss，那就是最小二乘；
如果损失函数是Hinge Loss，那就是著名的SVM；
如果损失函数是log-Loss，那就是Logistic Regression。

定义基学习器的集成为加权结合，则有：$$H(x)=\sum_{t=1}^{T} \alpha_{t} h_{t}(x)$$ AdaBoost算法的指数损失函数定义为：$$\text{loss}{\exp }(h)=\mathbb{E}, y}\left[e^{-y h(x)}\right]$$其中$-yh(x)$表示打标正确为负，打标错误为正。

具体说来，整个Adaboost迭代算法分为3步：

初始化训练数据的权值分布。如果有$N$个样本，则每一个训练样本最开始时都被赋予相同的权值：$1/N$。
训练弱分类器。具体训练过程中，如果某个样本点已经被准确地分类，那么在构造下一个训练集中，它的权值就被降低；相反，如果某个样本点没有被准确地分类，那么它的权值就得到提高。然后，权值更新过的样本集被用于训练下一个分类器，整个训练过程如此迭代地进行下去。
将各个训练得到的弱分类器组合成强分类器。各个弱分类器的训练过程结束后，加大分类误差率小的弱分类器的权重，使其在最终的分类函数中起着较大的决定作用，而降低分类误差率大的弱分类器的权重，使其在最终的分类函数中起着较小的决定作用。

Boosting 的核心思路是 —— 挑选精英。

　　Boosting 和 bagging 最本质的差别在于他对基础模型不是一致对待的，而是经过不停的考验和筛选来挑选出「精英」，然后给精英更多的投票权，表现不好的基础模型则给较少的投票权，然后综合所有人的投票得到最终结果。

大部分情况下，经过 boosting 得到的结果偏差（bias）更小。

具体过程：

通过加法模型将基础模型进行线性的组合。
每一轮训练都提升那些错误率小的基础模型权重，同时减小错误率高的模型权重。
在每一轮改变训练数据的权值或概率分布，通过提高那些在前一轮被弱分类器分错样例的权值，减小前一轮分对样例的权值，来使得分类器对误分的数据有较好的效果。

2.1.1 AdaBoost算法

2.1.1.1 什么是AdaBoost算法？

　　Boosting是一种集合技术，试图从许多弱分类器中创建一个强分类器。这是通过从训练数据构建模型，然后创建第二个模型来尝试从第一个模型中纠正错误来完成的。添加模型直到完美预测训练集或添加最大数量的模型。

　　AdaBoost是Adaptive Boosting的缩写，是由Yoav Freund和Robert Schapire制作的机器学习元算法，他们因其工作而获得2003年哥德尔奖。它可以与许多其他类型的学习算法结合使用，以提高性能。其他学习算法（“弱学习者”）的输出被组合成加权和，该加权和表示提升分类器的最终输出。

　　AdaBoost是第一个为二进制分类开发的真正成功的增强算法。这是理解助力的最佳起点。现代助推方法建立在AdaBoost上，最着名的是随机梯度增强机。

　　AdaBoost在某种意义上是适应性的，即随后的弱学习者被调整为支持那些被先前分类器错误分类的实例。AdaBoost对噪声数据和异常值敏感。在某些问题中，它可能比其他学习算法更不容易受到过度拟合问题的影响。个体学习者可能很弱，但只要每个学习者的表现略好于随机猜测，最终的模型就可以证明可以融合到强大的学习者身上。

　　AdaBoost可用于短决策树。在创建第一个树之后，每个训练实例上的树的性能用于加权创建的下一个树应该关注每个训练实例的注意力。难以预测的训练数据被赋予更多权重，而易于预测的实例被赋予更少的权重。模型一个接一个地顺序创建，每个模型更新训练实例上的权重，这些权重影响序列中下一个树所执行的学习。构建完所有树之后，将对新数据进行预测，并根据训练数据的准确性对每棵树的性能进行加权。

因为通过算法如此关注纠正错误，所以必须删除带有异常值的干净数据。

2.1.1.2 Adaboost 的优缺点

AdaBoost算法优点：

很好的利用了弱分类器进行级联；
可以将不同的分类算法作为弱分类器；
AdaBoost具有很高的精度；
相对于bagging算法和Random Forest算法，AdaBoost充分考虑的每个分类器的权重；

Adaboost算法缺点：

AdaBoost迭代次数也就是弱分类器数目不太好设定，可以使用交叉验证来进行确定；
数据不平衡导致分类精度下降；
训练比较耗时，每次重新选择当前分类器最好切分点；

2.1.1.3 AdaBoost算法推导过程

AdaBoost算法有多种推导方式，比较容易理解的是基于“加性模型”(additive model)，即基学习器的线性组合

\[H(x) = \sum \limits_{t=1}^T \alpha_t h_t(x)　\quad \quad (8.4) \]

式(8.4)的解释

注意到$h_t(x) \in \left\{-1, +1\right\}$，加权系数$\alpha_t$由后面的式(8.11)给出了(T个系数$\alpha_t$仅与自身对应的基学习器错误率$\epsilon_t$有关，相互之间无必然联系；由于要求$\epsilon_t < 0.5$，因此$\alpha_t > 0$)，所得线性加权结果$H(x)$就是一个实数，可能大于零，也可能小于零，取值范围无法确定。

来最小化指数损失函数(exponential loss function)

\[\ell_{exp}(H|\mathcal{D}) = \mathbb{E}_{x\simＤ}[e^{-f(x)H(x)}]. \quad \quad (8.5) \]

式(8.5)的解释

(1)先解释指数损失函数$e^{-f(x)H(x)}$的含义：$f$为真实函数，对于样本$x$来说，$f(x) \in \left\{-1, +1 \right\}$只能取-1和+1两个值，而$H(x)$是一个实数；
　　当$H(x)$的符号与$f(x)$一致时，$f(x)H(x) > 0$，因此$e^{-f(x)H(x)} = e^{-|H(x)|} < 1$，且$|H(x)|$越大指数损失函数$e^{-f(x)H(x)}$越小(这听起来很合理：此时$|H(x)|$越大意味着分类器本身对于预测结果的信心越大，但预测结果是错误，因此损失应该越大；若$|H(x)|$在零附近，虽然预测错误，但表示分类器本身对预测结果信息很小，虽然错乱，损失应该较小)；
　　对比0/1损失函数：当$H(x)$的符号与$f(x)$不一致时则损失为0，当$H(x)$的符号与$f(x)$不一致时则损失为1，而不管$H(x)$的大小。
(2)再解释符号$\mathbb{E}_{x \sim \mathcal{D}}[ \cdot]$的含义：$\mathcal{D}$为概率分布，可简单理解为在数据集$D$中进行一次随机抽样，每个样本被取到的概率:$\mathbb{E}[\cdot]$为经典的期望，则综合起来$\mathbb{E}_{x \sim \mathcal{D}}[\cdot]$表示在概率分布$\mathcal{D}$上的期望，可简单理解为对数据集$D$以概率$\mathcal{D}$进行加权后的期望。
　　综上所述，若数据集$D$中样本$x$的权值分布为$\mathcal{D}(x)$，则式(8.5)可写为:
　　　$\ell_{exp}(H|\mathcal{D}) = \mathbb{E}_{x \sim \mathcal{D}}[e^{-f(x)H(x)}] \\ =\sum \limits_{x \in D} \mathcal{D}(x)e^{-f(x)H(x)} \\ =\sum \limits_{x \in D} \mathcal{D}(x)(e^{-H(x)}\mathbb{I}(f(x) = 1) + e^{H(x)}\mathbb{I}(f(x) = -1))$

特别地，若针对任意样本$x$，若分布$\mathcal{D}(x) = \frac{1}{|D|}$，其中$|D|$为数据集$D$样本个数，则
　　　$\ell_{exp}(H|\mathcal{D}) = \mathbb{E}_{x \sim \mathcal{D}}[E^{-f(x)H(x)}] = \frac{1}{|D|} \sum \limits_{x \in D} e^{-f(x)H(x)}$.

而这就是在求传统平均值。

若$H(x)$能令指数损失函数最小化，则考虑$\ell_{exp}(H|\mathcal{D}) = \mathbb{E}_{x\simＤ}[e^{-f(x)H(x)}]$对$H(x)$的偏导

\[\frac{\partial \ell_{exp}(H|\mathcal{D})}{\partial H(x)} = -e^{-H(x)}P(f(x)=1|x) + e^{H(x)}P(f(x)=-1|x)　\quad \quad (8.6) \]

式(8.6)的推导

首先，当$f(x) = 1$时$e^{-f(x)H(x)} = e^{-H(x)}$,当$f(x) = -1$时$e^{-f(x)H(x)} = e^{H(x)}$；
其次，由以上分析可知式(8.5)包含$|D|$个不同的$e^{-f(x)H(x)}$，其中$x \in D$；
最后，针对每个$H(x)$求导，只有对应的$e^{-f(x)H(x)}$会起到作用，其余与$H(x)$无关的项求导后等于零。
为更方便理解，将式(8.5)的解释中的式(8.5)改写为如下形式
$\ell_{exp}(H|\mathcal{D}) = \mathbb{E}_{x \sim \mathcal{D}}[e^{-f(x)H(x)}] = \sum \limits_{i=1}^{|D|}\mathcal{D}(x_i)e^{-f(x_i)H(x_i)} \\ = \sum \limits_{i=1}^{|D|}\mathcal{D}(x_i)(e^{-H(x_i)}\mathbb{I}(f(x_i) = 1) + e^{H(x_i)}\mathbb{I}(f(x_i) = -1))$
但这里有点不同的是，式(8.6)是为了推导出式(8.7)和式(8.8)的判定准则预测$x$的类别，即无法得知$f(x)$具体等于$1$还是$-1$，只能知道$f(x)$为$1$的后验概率$P(f(x) = 1|x)$和为$-1$的后验概率$P(f(x) = -1|x)$，因此上式可写为
　　$\ell_{exp}(H|\mathcal{D}) = \sum \limits_{i=1}^{|D|}\mathcal{D}(x_i)\mathbb{E}[e^{-f(x_i)H(x_i)}] \\ = \sum \limits_{i=1}^{|D|}\mathcal{D}(x_i)(e^{-H(x_i)}P(f(x_i) = 1|x_i) + e^{H(x_i)}P(f(x_i) = -1|x_i)$
现对$H(x_i)$求导，求和项中只有第$i$项目$\mathcal{D}\mathbb{E}[e^{-f(x_i)H(x_i)}]$会起作用。$\mathcal{D}(x_i)$为常量，不影响接下来式(8.7)中令导数等于零求解的过程，而
　　　$\frac{\partial e^{-H(x)}}{\partial H(x)} = -e^{-H(x)}, \quad \frac{\partial e^{H(x)}}{\partial H(x)} = e^{H(x)}$
因此求导结果为
　　　$\frac{\partial \ell_{exp}(H|\mathcal{D})}{\partial H(x)} = -e^{-H(x)}P(f(x)=1|x) + e^{H(x)}P(f(x)=-1|x)$.
即为式(8.6)，得证。

令上式为零可解得

\[H(x) = \frac{1}{2}ln\frac{P(f(x)=1|x)}{P(f(x)=-1|x)} \quad \quad (8.7) \]

式(8.7)的推导

令式(8.6)等于零:$-e^{-H(x)}P(f(x)=1|x) + e^{H(x)}P(f(x)=-1|x) = 0$
移项：$e^{H(x)}P(f(x) = -1) = e^{-H(x)}P(f(x)=1|x)$
两边同乘$\frac{e^{H(x)}]}{P(f(x) = -1|x)}$: $e^{2H(x)} = \frac{P(f(x) = 1|x)}{P(f(x) = -1|x)}$；
取$ln(\cdot)$：$2H(x) = ln\frac{P(f(x) = 1|x)}{P(f(x) = -1|x)}$；
两边同除$2$:即可得$H(x) = \frac{1}{2}ln\frac{P(f(x)=1|x)}{P(f(x)=-1|x)}$。
至此，式(8.7)得证。

因此，有

\[sign(H(x)) = sign \left(\frac{1}{2}ln\frac{P(f(x)=1|x)}{P(f(x)=-1|x)}\right) \\ =　\left\{\begin{matrix} 1,\quad P(f(x)=1|x) > P(f(x)=-1|x)\\ -1,\quad P(f(x)=1|x) <P(f(x)=-1|x) \end{matrix}\right. \\ = \underset{y∈\left\{-1,1\right\}}{arg　max}P(f(x)=y|x) \quad \quad (8.8) \]

这意味着$sign(H(x))$达到了贝叶斯最优错误率。换言之，若指数损失函数最小化，则分类错误率也将最小化；
这说明指数损失函数是分类任务原来$0/1$损失函数的一致的(consistent)替代损失函数。由于这个替代函数有更好的数学性质，例如它是连续可微函数，因此我们用它来替代$0/1$损失函数作为优化目标。

　　在AdaBoost算法中，第一个基分类器$h1$是通过直接将基学习算法用于初始数据分布而得；此后迭代地生成$h_t$和$\alpha_t$，当基分类器$h_t$基于分布$\mathcal{D}_t$产生后，该基分类器的权重$a_t$应使得$\alpha_th_t$最小化损失函数。

\[\ell_{exp}(\alpha_t h_t|\mathcal{D_t}) = \mathbb{E}_{x\sim \mathcal{D}_t} \left[e^{-f(x)\alpha_t h_t(x)} \right] \\ = \mathbb{E}_{x\sim \mathcal{D}_t} \left[e^{-\alpha_t}\mathbb{I}f((x)=h_t(x)) + e^{\alpha_t}\mathbb{I}(f(x)\neq h_t(x)) \right] \\ = e^{-\alpha_t}P_{x\sim \mathcal{D}_t}(f(x)=h_t(x)) + e^{\alpha_t}P_{x\sim \mathcal{D_t}}(f(x)\neq h_t(x)) \\ = e^{-\alpha_t}(1-\epsilon_t) + e^{\alpha_t}\epsilon_t \quad \quad (8.9) \]

式(8.9)的解释

第一个等号与式(8.5)的区别仅在于到底针对$\alpha_th_t$还是$H(x)$，代入即可；
第二个等号是考虑到$h_t(x)$和$f(x)$均只能取-1和+1两个值，其中$\mathbb{I}(\cdot)$为指示函数；
第三个等号对中括号的两项分别求$\mathbb{E}_{x \sim \mathcal{D}}[\cdot]$，而$e^{\alpha_t}$和$e^{\alpha_t}$与$x$无关，可以作为常数项拿到$\mathbb{E}_{x \sim \mathcal{D}_t}[\cdot]$外面，而$\mathbb{E}_{x \sim \mathcal{D}_t}[\mathbb{I}(f(x) = h_t(x))]$表示在数据集D上、样本权值分布为$\mathcal{D}_t$时$f(x)$和$h_t(x)$相等次数的期望，即$P_{x \sim \mathcal{D}_t}(f(x) = h_t(x))$，也就是是正确率，即$(1 - \epsilon_t)$；
同理，$\mathbb{E}_{x \sim \mathcal{D}_t}[\mathbb{I}(f(x) \neq h_t(x))]$表示在数据集$D$上、样本权值分布为$\mathcal{D}_t$时$f(x)$和$h_t(x)$不相等次数的期望，即$P_{x \sim \mathcal{D}_t}(f(x) \neq h_t(x))$，也就是错误率$\epsilon_t$；
第四个等号即为将$P_{x \sim \mathcal{D}_t}(f(x) = h_t(x))$替换为$(1 - \epsilon_t)$、将$P_{x \sim \mathcal{D}_t}(f(x) \neq h_t(x))$替换为$\epsilon_t$的结果。

其中$\epsilon_t=P_{x\sim \mathcal{D}_t}(h_t(x)\neq f(x))$。

下面考虑指数损失函数的导数

\[\frac{\partial \ell_{exp}(\alpha_t h_t|\mathcal{D}_t)}{\partial \alpha_t} = -e^{-\alpha_t}(1-\epsilon_t) + e^{\alpha_t}\epsilon_t \quad \quad (8.10) \]

令上式为零可解得

\[\alpha_t = \frac{1}{2}ln(\frac{1-\epsilon_t}{\epsilon_t}) \quad \quad (8.11) \]

这恰是AdaBoost算法迭代中的分类器权重更新公式。

AdaBoost算法在获得$H_{t-1}$之后样本分布将进行调整，使下一轮的基学习器$h_t$能纠正$H_{t-1}$的一些错误。
理想的$h_t$能纠正$H_{t-1}$的全部错误，即最小化

\[\ell_{exp}(H_{t-1} + h_t|\mathcal{D}) = \mathbb{E}_{x \sim D}[e^{-f(x)}(H_{t-1}(x) + h_t(x))] \\ = \mathbb{E}_{x\sim \mathcal{D}}[e^{-f(x)H_{t-1}(x) e^{-f(x)h_t(x)}}]. \quad \quad (8.12) \]

注意到$f^2(x) = h_t^2(x) = 1$，上式可以使用$e^{-f(x)h_t(x)}$的泰勒展开式近似为

\[\ell_{exp}(H_{t-1}+h_t|\mathcal{D})\simeq \mathbb{E}_{x\sim \mathcal{D}}\left[e^{-f(x)H_{t-1}(x)}(1-f(x)h_t(x)+\frac{f^2(x)h_t^2(x)}{2} \right] \\ = \mathbb{E}_{x\sim \mathcal{Ｄ}} \left[e^{-f(x)H_{t-1}(x)}(1-f(x)h_t(x) + \frac{1}{2} \right] \quad \quad (8.13) \]

式(8.13)的推导

复习以下泰勒展开式:
$f(x) = \frac{f(x_0)}{0!} + \frac{f'(x_0)}{1!}(x-x_0) + \frac{f''(x_0)}{2!}(x-x_0)^2 + ... + \frac{f^{(n)}(x_0)}{n!}(x - x_0)^n + ...$
当$f(x) = e^{-x}$时，在$x_0$处泰勒展开：
$e^{-x}$时，在$x_0$处泰勒展开，代入即可得式(8.13)。
实际上，此处保留一阶泰勒展开项即可，后面提到的Gradient Boosting理论框架就是只使用了一阶泰勒展开；当然二阶项为常数，也并不影响推导结果，原文献中保留了二阶项。

于是，理想的基学习器

\[\begin{align} &h_t(x) = \mathop{\arg\min}_{h} \ell_{exp}(H_{t-1}+h|\mathcal{D}) \\ &= \mathop{\arg\min}_{h}\mathbb{E}_{x\sim \mathcal{D}} \left[e^{-f(x)H_{t-1}(x)} \left(1-f(x)h(x) + \frac{1}{2} \right) \right] \\ &= \mathop{\arg\min}_{h}\mathbb{E}_{x\sim \mathcal{D}} \left[e^{-f(x)H_{t-1}(x)}f(x)h(x) \right] \\ &= \mathop{\arg\min}_{h}\mathbb{E}_{x\sim \mathcal{D}} \left[\frac{e^{-f(x)H_{t-1}(x)}}{\mathbb{E}_{x\sim \mathcal{D}} [e^{-f(x)H_{t-1}(x)}]}f(xh(x)) \right] \quad \quad (8.14) \end{align} \]

式(8.14)的推导

本式基于式(8.12)和式(8.13)的结果。理想的$h_t(x)$是使得$H_t(x)$的指数损失函数取得最小值时的$h_t(x)$，该式将次转化成某个期望的最大值。
第二个等号就是在第一个等号的基础上将式(8.13)代入；
第三个等号是因为
$\mathbb{E}_{x \sim \mathcal{D}} \left[e^{-f(x)H_{t-1}(x)} \left(1 - f(x)h(x) + \frac{1}{2} \right) \right] \\ = \mathbb{E}_{x \sim \mathcal{D}} \left[\frac{3}{2} e^{-f(x)H_{t-1}(x)} - e^{-f(x)H_{t-1}(x)}f(x)h(x) \right] \\ = \mathbb{E}_{x \sim \mathcal{D}} \left[\frac{3}{2}e^{-f(x)H_{t-1}(x)} \right] - \mathbb{E}_{x \sim \mathcal{D}} \left[e^{-f(x)H_{t-1}(x)}f(x)h(x) \right]$
本式自变量为$h(x)$，而$\mathbb{E}_{x \sim \mathcal{D}}[\frac{3}{2}e^{-f(x)H_{t-1}}(x)]$与$h(x)$无关，也就是一个常数；
这时我们只需最大化第二项$\mathbb{E}_{x \sim \mathcal{D}}[e^{-f(x)H_{t-1}(x)}f(x)h(x)]$即可，将负号去掉，则原最小化问题变为最大化问题；
第四个等号仍是因为$\mathbb{E}_{x \sim \mathcal{D}}[e^{-f(x)H_{t-1}(x)}]$是与自变量$h(x)$无关的正常数(因为指数函数$e^{-f(x)H_{t-1}(x)}$大于零，从而求期望$\mathbb{E}_{x \sim \mathcal{D}}[\cdot]$的结果也大于零)，而最大化问题乘以某个正常数与原问题等价(例如$\arg \max_x(1 - x^2)$与$\arg \max_x 2(1-x^2)$的结果均为$x = 0$)；

注意到$\mathbb{E}_{x\sim \mathcal{D}} [e^{-f(x)H_{t-1}(x)}]$是一个常数。

则令$\mathcal{D}_t$表示一个分布

\[\mathcal{D}_t(x) = \frac{\mathcal{D}(x) e^{-f(x)H_{t-1}(x)}}{\mathbb{E}_{x\sim \mathcal{D}}[e^{-f(x)H_{t-1}(x)}]} \quad \quad (8.15) \]

则根据数据期望的定义，这等价于令

\[h_t(x) = \mathop{\arg\min}_{h} \mathbb{E}_{x\sim \mathcal{D}} \left[\frac{e^{-f(x)H_{t-1}(x)}}{\mathbb{E}_{x\sim \mathcal{D}}[e^{-f(x)H_{t-1}(x)}]}f(x)h(x) \right] \\ = \mathop{\arg\min}_{h} \mathbb{E}_{x\sim \mathcal{D_t}}[f(x)h(x)] \quad \quad (8.16) \]

式(8.16)的推导

首先解释以下符号$\mathbb{E}_{x \sim \mathcal{D}}$的含义，这里注意在本章有两个符号$D$和$\mathcal{D}$，其中$D$表示数据集，而$\mathcal{D}$表示数据集$D$的样本分布，可以理解为在数据集$D$上进行一次随机采样，则样本$x$被抽到的概率为$\mathcal{D}(x)$，那么符号$\mathbb{E}_{x \sim \mathcal{D}}$表示的是在概率分布$\mathcal{D}$上的期望，可以简单理解为对数据及$D$以概率$\mathcal{D}$加权之后的期望。
因此，类似于式(8.6)的推导中：
　　　　$\mathbb{E}_{x \sim \mathcal{D}}[e^{-f(x)H(x)}] = \sum \limits_{i=1}^{|D|}e^{-f(x_i)H(x_i)}$
并结合式(8.15)的定义可知
　　　　$\mathcal{D}_t(x_i) = \mathcal{D}(x_i) \frac{e^{-f(x_i)H_{t-1}(x_i)}}{\mathbb{E}_{x \sim \mathcal{D}}[e^{-f(x)H_{t-1}(x)}]}$
其中$x_i$表示数据集D的第$i$个样本，故与式(8.15)一样。
所以针对式(8.14式的最后一行表达式，(8.16可以表示为
　　　　$\mathbb{E}_{x \sim \mathcal{D}} \left[\frac{e^{-f(x)H_{t-1}(x)}}{\mathbb{E}_{x \sim \mathcal{D}[e^{-f(x)H_{t-1}(x)}]}}f(x)h(x) \right] \\ = \sum \limits_{i=1}^{|D|}\mathcal{D}(x_i) \frac{e^{-f(x_i)H_{t-1}(x_i)}}{\mathbb{E}_{x \sim \mathcal{D}}[e^{-f(x}H_{t-1}(x)]}f(x_i)h(x_i) \\ = \sum \limits_{i=1}^{|D|}\mathcal{D}_t(x_i)f(x_i)h(x_i) \\ = \sum \limits_{x \sim \mathcal{D}_t}[f(x)h(x)]$

由$f(x),h(x)∈\left\{-1,+1 \right\}$有

\[f(x)h(x) = 1 - 2 \mathbb{I}(f(x) \neq h(x)) \quad \quad (8.17) \]

式(8.17)的推导

当$f(x) = h(x)$时，$f(x)h(x) = 1$；
当$f(x) \neq h(x)$，$f(x)h(x) = -1$；
当$f(x) = h(x)$时，$\mathbb{I}(f(x) \neq h(x)) = 0$，则$1 - 2\mathbb{I}(f(x) \neq h(x)) = 1$；
当$f(x) \neq h(x)$时，$\mathbb{I}(f(x) \neq h(x)) = 1$，则$1 - 2\mathbb{I}(f(x) \neq h(x)) = -1$；
综上所述，等式两边相等。

则理想的基学习器

\[h_t(x) = \mathop{\arg\min}_{h} \mathbb{E}_{x\sim \mathcal{D}_t} [\mathbb{I}f(x) \neq h(x)] \quad \quad (8.18) \]

式(8.18)的推导

本式基于式(8.17)的恒等关系，由式(8.16)推导而来。
　　　$\mathbb{E}_{x \sim \mathcal{D}}[f(x)h(x)] = \mathcal{E}_{x \sim \mathcal{D}_t}[1 - 2\mathbb{I}(f(x)) \neq h(x)] \\ =\mathbb{E}_{x \sim \mathcal{D_t}[1] - 2\mathbb{E}_{x \sim \mathcal{D}_t}}[\mathbb{I}(f(x) \neq h(x))]$

类似于式(8.14)的第3个和第4个等号，由式(8.16)的结果开始推导:
$h_t(x) = \mathop{\arg\max} \limits_{h} \mathbb{E}_{x \sim \mathcal{D}_t}[f(x)h(x)] \\ = \mathop{\arg\max} \limits_{h} (1 - 2 \mathbb{E}_{x \sim \mathcal{D}_t})[\mathbb{I}(f(x) \neq h(x))] \\ = \mathop{\arg\max} \limits_{h} (1 - 2\mathbb{E}_{x \sim \mathcal{D}_t)}[\mathbb{I}(f(x) \neq h(x))] \\ = \mathop{\arg\min} \limits_{h} \mathbb{E}_{x \sim \mathcal{D}_t} [\mathbb{I}(f(x) \neq h(x))]$
此式表示理想的$h_t(x)$在分布$\mathcal{D}_t$下最小化分类误差，因此有图8.3第3行$h_t(x) = \mathcal{L}(D, \mathcal{D}_t)$，即分类器$h_t(x)$可以基于分布$\mathcal{D}_t$从数据集$D$中训练而得，而我们在训练分类器时一般来说最小化的损失函数就是分类误差。

由此可见，理想的$h_t$将在分布$\mathcal{D}_t$下最小化分类误差。
因此，弱分类器将基于分布$\mathcal{D}_t$来训练，且针对$\mathcal{D}_t$的分类误差应小于0.5。这在一定程度上类似于“残差逼近”的思想。考虑到$\mathcal{D}_t$和$\mathcal{D}_{t+1}$的关系，有

\[\mathcal{D}_{t+1} = \frac{\mathcal{D}(x) e^{-f(x)H_t(x)}}{\mathbb{E}_{x\sim \mathcal{D}}[e^{-f(x)H_{t}(x)}]} \\ =　\frac{\mathcal{D}(x) e^{-f(x)H_{t-1}(x)}e^{-f(x)\alpha_th_t(x)}}{\mathbb{E}_{x\sim \mathcal{D}}[e^{-f(x)H_t(x)}]} \\ = \mathcal{D}_t(x)\cdot e^{-f(x)\alpha_t h_t(x)} \frac{\mathbb{E}_{x\sim \mathcal{D}}[e^{-f(x)H_{t-1}(x)}]}{\mathbb{E}_{x\sim \mathcal{D}}[e^{-f(x)H_t(x)}]} \quad \quad (8.19) \]

这恰是AdaBoost算法迭代中的样本分布更新公式。

式(8.19)的推导

boosting算法是根据调整后的样本再去训练下一个基分类器，这就是“重赋权法”的样本分布的调整公式。
对于上式(8.19)，第一个等号是将式(8.15)中的$t$换成$t+1$(同时$t-1$换成$t$)；
第二个等号是将$H_t(x) = H_{t-1}(x) + \alpha_th_t(x)$代入分子即可；
第三等号是乘以$\frac{\mathbb{E}_{x \sim \mathcal{D}}[e^{-f(x)H_{t-1}(x)}]}{\mathbb{E}_{x \sim \mathcal{D}[e^{-f(x)H_{t-1}(x)}]}}$后，凑出式(8.15)的$\mathcal{D}_t(x)$，以符号$\mathcal{D}_t(x)$替换即得。
到此之后，得到$\mathcal{D}_{t+1}(x)$与$\mathcal{D}_t(x)$的关系，但为了确保$\mathcal{D}_{t+1}(x)$是一个分布，需要对得到的$\mathcal{D}_{t+1}(x)$进行规范化，即图8.3第7行的$Z_t$。式(8.19)第3行最后一个分式将在规范化过程中被吸收。

于是，由$\alpha_t = \frac{1}{2}ln(\frac{1-\epsilon_t}{\epsilon_t})$和$\mathcal{D}_{t+1} = \mathcal{D}_t(x)\cdot e^{-f(x)\alpha_t h_t(x)} \frac{\mathbb{E}_{x\sim \mathcal{D}}[e^{-f(x)H_{t-1}(x)}]}{\mathbb{E}_{x\sim \mathcal{D}}[e^{-f(x)H_t(x)}]}$可见,我们基于加性模型迭代式优化指数损失函数的角度推导出了AdaBoost算法。

2.1.2 AdaBoost推导梳理

2.1.3 AdaBoost算法描述

整个AdaBoost的算法描述如下所示：(其中$y_i∈\left\{-1,+1\right\}$,$f$是真实函数。)(参考-西瓜书)

输入：训练集$D=\{(x_1,y_1),(x_2,y_2),\ldots,(x_m,y_m)\}$；
基学习算法$\mathcal{L}$；
训练轮数$T$；
过程：
  1: 初始化权重：$D_1(i)=1/m$
  2: for $t=1,\cdots,T$:
  3:   $h_t=\mathcal{L}(D,D_t)$；用$D$和$D_t$训练一个学习器$h_t$；
  4:   $\epsilon_t=Pr_{x \sim D_{t,y}}I[h_t(x) \neq y]$；计算$h_t$的误差；
  5:   if $\epsilon > 0.5$ then break
  6:   $\displaystyle \alpha_t=\frac{1}{2} \ln \left(\frac{1-\epsilon_t}{\epsilon_t} \right)$；计算基学习器权重；
$\begin{aligned} \text{7:} \quad D_{t+1}(i) &=\displaystyle \frac{D_{t}(i)}{Z_{t}} \times\left\{\begin{array}{l}{\exp (-\alpha_t) \text { if } h_{t}(x_i)=y_i} \\ {\exp (\alpha_t) \quad \text { if } h_{t}(x_i) \neq y_i}\end{array}\right. \\ &=\displaystyle \frac{D_t(i) \exp(-\alpha_t y_i h_t(x_i))}{Z_t} \end{aligned}$
    样本权重分布更新；
  8: end for
输出：$\displaystyle H(x)=\text{sign}(\sum_{t=1}^T \alpha_t h_t(x)) $

2.1.3.1 AdaBoost算法详解

这里进一步深入叙述AdaBoost算法(参考《统计学习方法》)。
假设给定一个二类分类的训练数据集合

\[T = \left\{(x_1,y_1),(x_2,y_2),...,(x_N，y_N) \right\} \]

其中，每个样本点由实例与标记组成。实例$x_i∈\mathcal{X}\subseteqＲ^2$，标记$y_i∈\mathcal{Y}=\left\{-1,+1 \right\}$，$\mathcal{X}$是实例空间，$\mathcal{Y}$是标记集合。AdaBoost利用以下算法，从训练数据中学习一系列弱分类器或基本分类器，并将这些弱分类器线性组合成为一个强分类器。
输入：训练数据集$T = \left\{(x_1,y_1),(x_2,y_2),...,(x_N，y_N) \right\}$,其中$x_i∈\mathcal{X}\subseteqＲ^2$,$y_i∈\mathcal{Y}=\left\{-1,+1 \right\}$；弱学习算法
输出：最终分类器G(x)
(1)初始化训练数据的权值分布

\[D_1 = (w_{11},...,w_{1i},...,w_{1N}), \quad w_{1i} = \frac{1}{N}, i = 1,2,...,N \]

(2)对$m=1,2,...,M$.
　　(a) 使用具有权值分布$D_m$的训练数据集学习，得到基本分类器.

\[G_m(x):\mathcal{X} \to \left\{-1,+1\right\} \]

　　(b) 计算$G_m(x)$在训练数据集上的分类误差率.

\[e_m = \sum \limits_{i=1}^N P(G_m(x_i) \neq y_i) = \sum \limits_{i=1}^N W_{mi}I(G_m(x_i)\neq y_i) \]

　　(c)计算$G_m(x)$的系数.

\[\alpha_m = \frac{1}{2} log \frac{1-e_m}{e_m} = \frac{1}{2}ln\frac{1-e_m}{e_m} \]

　　　　这里的对数是自然对数
　　(d)更新训练数据集的权值分布.

\[D_{m+1} = (w_{m+1,1},...,w_{m+1,i},...,w_{m+1,N})　\\ w_{m+1,i} = \frac{w_{mi}}{Z_{m}} exp(-\alpha_m y_iG_m(x_i)), \quad i=1,2,...,N \]

　　　　　这里的$Z_m$是规范化因子,它使$D_{m+1}$成为一个概率分布。

\[Z_m = \sum \limits_{i=1}^N w_{mi} exp(-\alpha_m y_i G_m(x_i)) \]

(3)构建基本分类器的线性组合.

\[f(x) = \sum \limits_{m=1}^M \alpha_m G_m(x) \]

得到最终分类器

\[G(x) = sign(f(x)) = sign(\sum \limits_{m=1}^M \alpha_m G_m(x)) \]

对AdaBoost算法作如下说明:
　　步骤(1)　假设训练数据集具有均匀的权重分布，即每个训练样本在基本分类器的学习中作用相同，这以假设保证第1步能够在原始数据上学习基本分类器$G_1(x)$.
　　步骤(2)　AdaBoost反复学习基本分类器，在每一轮$m=1,2,...,M$顺次地执行下列操作:
　　　　(a) 使用当前分布$D_m$加权的训练数据集，学习基本分类器$G_m(x)$．
　　　　(b) 计算基本分类器$G_m(x)$在加权训练数据集上的分类误差率:

\[e_m = \sum \limits_{i=1}^N P(G_m(x_i)\neq y_i) = \sum \limits_{G_m(x_i)\neq y_i}w_{mi}. \]

　　　　这里，$w_{mi}$表示第m轮中第$i$个实例的权值，$\sum \limits_{i=1}^N w_{mi}=1$。
　　　　这表明基本分类器$G_m(x)$在加权的训练数据集上的分类误差率是被$G_m(x)$误分类样本的权值之和。
　　　　由此可以看出数据权重分布$D_m$与基本分类器$G_m(x)$的分类误差率的关系。
　　　　(c) 计算基本分类器$G_m(x)$的系数$\alpha_m$。$\alpha_m$表示$G_m$表示$G_m(x)$在最终分类器中的重要性。
　　　　由$\alpha_m = \frac{1}{2}ln\frac{1-e_m}{e_m}$可知，当$e_m\leq \frac{1}{2}$时，$\alpha_m\geq 0$，并且$\alpha_m$随着$e_m$的减小而增大。
　　　　所以分类误差率越小的分类器在最终分类器中的作用越大。
　　　　(d) 更新训练数据的权重分布为下一轮作准备。
　　　　$w_{m+1,i} = \frac{w_{mi}}{Z_{m}} exp(-\alpha_m y_iG_m(x_i)), \quad i=1,2,...,N$可以写成

\[w_{m+1,i} = \left\{\begin{matrix} \frac{w_{mi}}{Z_{m}}e^{-\alpha_m}, \quad G_m(x_i) = y_i \\ \frac{w_{mi}}{Z_m}e^{\alpha_m}, \quad G_m(x_i) \neq y_i \end{matrix}\right. \]

　　　　由此可知，被基本分类器$G_m(x)$误分类样本的权值得以扩大，而被正确分类样本的权值却得以缩小。
　　　　两相比较，由$\alpha_m = \frac{1}{2}ln\frac{1-e_m}{e_m}$知误分类样本的权值被放大$e^{2\alpha_m} = \frac{1-e_m}{e_m}$倍。
　　　　因此，误分类样本在下一轮学习中起更大的作用。
　　　　不改变所给的训练数据，而不断改变训练数据权值的分布，
　　　　使得训练数据在基本分类器的学习中起不同的作用，这是AdaBoost的一个特点。

　　步骤(3)　线性组合$f(x)$实现Ｍ个基本分类器的加权表决。
　　系数$\alpha_m$表示了基本分类器$G_m(x)$的重要性，这里，所有$\alpha_m$之和并不为1。
　　$f(x)$的符号决定实例$x$的类，$f(x)$的绝对值表示分类的确信度。
　　利用基本分类器的线性组合构建最终分类器是AdaBoost的另一个特点。

重赋权法：　
Boosting算法要求基学习器能对特定的数据分布进行学习，这可通过“重赋权法”(re-weighting)实施，即在训练过程的每一轮中，根据样本分布为每个训练样本重新赋予一个权重，即在训练过程的每一轮中，根据样本分布为每个训练样本重新赋予一个权重。
重采样法：
对无法接受带权样本的基学习算法，则可通过“重采样法”(re-sampling)来处理，即在每一轮学习中，根据样本分布对训练集重新进行采样，再用重采样而得的样本集对基学习器进行训练。

　　一般而言，这两种做法没有显著的优劣差别。但需要注意的是，Boosting算法在训练的每一轮都要检查当前生成的基学习器是否满足基本条件(例如，检查当前基分类器是否是比随机猜测好)，一旦条件不满足，则当前基学习器即被抛弃，且学习过程停止。在此种情形下，初始设置的学习轮数Ｔ也许还远未达到，可能导致最终集成中只包含很少的基学习器而性能不佳。

　　若采用“重采样法”，则可获得“重启动”机会以避免训练过程停止，即在抛弃不满足条件的当前基学习器之后，可根据当前分布重新对训练样本进行采样，再基于新的采样结果重新训练出基学习器，从而使得学习过程可以持续到预设的Ｔ轮完成。
　　
　　从偏差－方差分解的角度看，Boosting主要关注降低偏差，因此Boosting能基于泛化性能相当弱的学习器构建出很强的集成。从AdaBoost的算法流程来看，标准的AdaBoost只适用于二分类问题。

　　我们以决策树桩为基学习器，在西瓜数据集$3.0\alpha$上运行AdaBoost算法，不同规模(size)的集成及其基学习器所对应的分类边界如下所示。

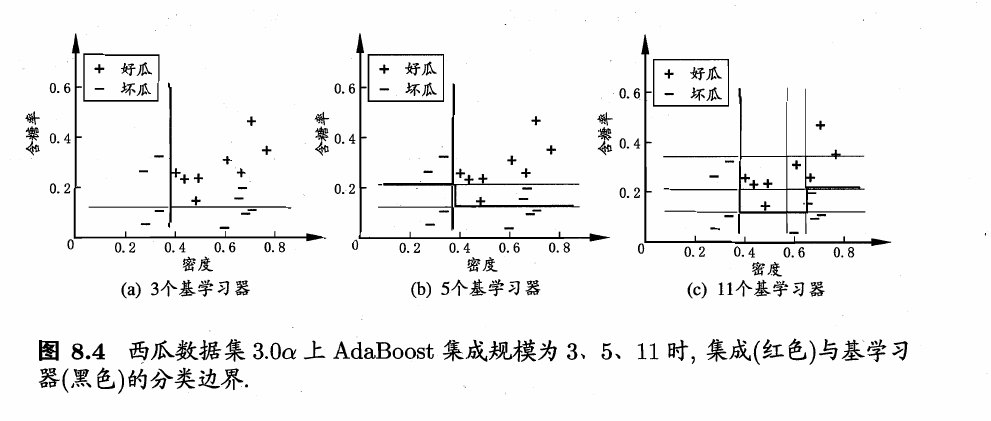
例题1 试用AdaBoost算法学习一个强分类器。

给定如下表所示的训练数据。假设弱分类器由$x<v$或$x>v$产生，其阈值$v$使该分类器在训练数据集上分类误差率最低。试用AdaBoost算法学习一个强分类器。

解　初始化数据权重分布

\[D_1 = (w_{1,1},w_{1,2},...,w_{1,10}) \]

第一轮对m=1,
　　(a) 在权重分布为$D_1$的训练数据上，阈值$v$取2.5时分类误差率最低，故基本分类器为

\[G_1(x) = \left\{\begin{matrix} 1, \quad x < 2.5 \\ -1, \quad x> 2.5 \end{matrix}\right. \]

　　(b) $G_1(x)$在训练数据集上的误差率$e_1 = P(G_1(x_i)\neq y_i)=0.3$。
　　(c) 计算$G_1(x)$的系数：$\alpha_1 = \frac{1}{2}log\frac{1-e_1}{e_1}=0.4236$。
　　(d) 更新训练数据的权值分布:

\[D_2 = (w_{2,1},...,w_{2,i},...,w_{2,10}) \\ w_{2,i} = \frac{w_{1,i}}{Z_1}exp(-\alpha_1 y_i G_1(x_i)), \quad i = 1,2,...,10 \\ D_2 = (0.07143,0.07143,0.07143,0.07143,0.07143,0.07143,\\0.16667, 0.16667,0.16667,0.07143)　\\ f_1(x) = 0.4236G_1(x) \]

对分类器sign[$f_1(x)$]在训练数据上有3个误分类点。

第二轮对m=2,
　　(a) 在权重分布为$D_2$的训练数据上，阈值$v$取8.5时分类误差率最低，故基本分类器为

\[G_2(x) = \left\{\begin{matrix} 1, \quad x < 8.5 \\ -1, \quad x> 8.5 \end{matrix}\right. \]

　　(b) $G_2(x)$在训练数据集上的误差率$e_2 = P(G_2(x_i)\neq y_i)=0.2143$。
　　(c) 计算$G_2(x)$的系数：$\alpha_2 = \frac{1}{2}log\frac{1-e_2}{e_2}=0.6496$。
　　(d) 更新训练数据的权值分布:

\[D_3 = (0.0455,0.0455,0.0455,0.16667,0.16667,\\0.16667,0.1060,0.1060,0.1060,0.0455)　\\f_2(x) = 0.4236G_1(x) + 0.6496G_2(x). \]

对分类器sign[$f_2(x)$]在训练数据上有3个误分类点。

第三轮对m=3,
　　(a) 在权重分布为$D_3$的训练数据上，阈值$v$取5.5时分类误差率最低，故基本分类器为

\[G_3(x) = \left\{\begin{matrix}1, \quad x < 5.5 \\-1, \quad x > 5.5\end{matrix}\right. \]

　　(b) $G_2(x)$在训练数据集上的误差率$e_3 = P(G_3(x_i)\neq y_i)=0.1820$。
　　(c) 计算$G_3(x)$的系数：$\alpha_3 = \frac{1}{2}log\frac{1-e_3}{e_3}=0.7514$。
　　(d) 更新训练数据的权值分布:

\[D_4 = (0.125,0.125,0.125,0.102,0.102,0.102,0.065,0.065,0.065,0.125) \]

　　于是得到:

\[f_3(x) = 0.4236G_1(x) + 0.6496G_2(x) + 0.7514G_3(x). \]

　　对分类器sign[$f_3(x)$]在训练数据上有0个误分类点。

于是最终分类器为

\[Ｇ(x) = sign[f_3(x)] = sign[0.4236G_1(x) + 0.6496G_2(x) + 0.7514G_3(x)] \]

(三) Bagging与随机森林

　　与AdaBoost算法相比，Bagging与随机森林算法就简洁许多，我们知道产生“好而不同”的个体学习器是集成学习研究的核心，即在保证基学习器准确性的同时增加基学习器之间的多样性。而这两种算法的基本思想都是通过“自助采样法”来增加多样性。

　　由前面的讨论中，我们可以知道，欲得到泛化性能强的集成，集成中的个体学习器应尽可能独立；虽然“独立”在现实任务中无法做到，但可以设法使基学习器尽可能具有较大的差异。给定一个训练数据集，一种可能的做法是对训练样本进行采样，产生出若干个不同的子集，再从每个数据子集中训练出一个基学习器。

　　这样，由于训练数据不同，我们获得的基学习器可望具有比较大的差异。然而，为获得好的集成，我们同时还希望个体学习器不能太差。如果采样出的每个子集都完全不同，则每个基学习器只用到了一小部分训练数据，甚至不足以进行有效学习，这显然无法确保产生出比较好的基学习器。为解决这个问题，我们可考虑使用相互有交叠的采样子集。　

3.1 Bagging

　　Bagging是并行式集成学习方法著名的代表。从名字即可看出，它直接基于我们之前介绍过的自助采样法(bootstrap sampling)。给定包含m个样本的数据集，我们先随机取出一个样本放入采样集中，再把该样本放回初始数据集，使得下次采样时该样本仍有可能被选中，这样，经过m次随机采样操作，我们得到m个样本的采样集合，初始训练集中有的样本在采样集里多次出现，有的则从未出现，则样本在m次采样中始终不被采到的概率为$(1-\frac{1}{m})^m$,取极限可得

\[\lim_{m \longmapsto \infty}(1-\frac{1}{m})^m \longmapsto \frac{1}{e}\approx 0.368 = 36.8\% \]

由此可知，初始训练集中约有63.2%的样本出现在采样集中。

3.1.1 Bagging的基础流程

　　Bagging 的核心思路是 — — 民主。
　　Bagging 的思路是所有基础模型都一致对待，每个基础模型手里都只有一票。然后使用民主投票的方式得到最终的结果。大部分情况下，经过 bagging 得到的结果方差（variance）更小。

　　照这样，我们可采样出T个含m个训练样本的采样集，然后基于每个采样集训练出一个基学习器，再将这些基学习器进行结合。这就是Bagging的基础流程。

　　在对预测输出进行结合时，Bagging通常对分类任务使用简单投票法，对回归任务使用简单平均法。若分类预测时出现两个同样票数的情形，则最简单的做法是随机选择一个，也可进一步考察学习器投票的置信度来确定最终胜者。

具体过程：

从原始样本集中抽取训练集。每轮从原始样本集中使用Bootstraping的方法抽取n个训练样本（在训练集中，有些样本可能被多次抽取到，而有些样本可能一次都没有被抽中）。共进行k轮抽取，得到k个训练集。（k个训练集之间是相互独立的）
每次使用一个训练集得到一个模型，k个训练集共得到k个模型。（注：这里并没有具体的分类算法或回归方法，我们可以根据具体问题采用不同的分类或回归方法，如决策树、感知器等）
对分类问题：将上步得到的k个模型采用投票的方式得到分类结果；对回归问题，计算上述模型的均值作为最后的结果。（所有模型的重要性相同）

3.1.2 Bagging算法描述

输入：训练集$D=\{(x_1,y_1),(x_2,y_2),\ldots,(x_m,y_m)\}$；
基学习算法$L$；
训练轮数$T$；
过程：
  1: for $t=1,2,\cdots,T$ do
  2:   $h_t=L(D,D_{bs})$；
  3: end for
输出：$H(x)=\underset{y \in \mathcal{Y}}{\arg \max } \sum_{t=1}^{T} I\left(h_{t}(x)=y\right)$　　

　　假定基学习器的计算复杂度为O(m)，则Bagging的复杂度大致为T(0(m)+0(s))，考虑到采样与投票/平均过程的复杂度O(s)很小，而Ｔ通常是一个不太大的常数，因此，训练一个Bagging集成与直接使用基学习算法训练一个学期器的复杂度同阶，这说明Bagging是一个很高效的集成学习算法。另外，与标准AdaBoost只适用于二分类任务不同，Bagging能不经修改地用于多分类、回归等任务。

　　值得一提的是，自助采样过程除了简单高效之外，还给Bagging带来了另一个优点：由于每个基学习器只使用了初始训练集中约63.2%的样本，剩下约36.8%的样本可用作验证集来对泛化性能进行“包外估计”(out-of-bag estimate)。

　　为此需记录每个基学习器所使用的训练样本。不妨令$D_t$表示分类器$h_t$实际使用的训练样本集，令$h^{oob}$表示对样本$x$的包外预测，即仅考虑那些未使用$x$训练的基学习器在$x$上的预测，有

\[H^{oob}(x) = \mathop{arg\max}_{y∈\mathcal{Y}}\sum \limits_{t=1}^T\mathbb{I}(h_t(x)=y)\cdot \mathbb{I}(x∉D_t) \quad \quad (8.20) \]

式(8.20)的解释

仅注意一点即可，每个基分类器对应的36.8%的剩余样本均是不同的(可能会有样本出现在多个基分类器对应的36.8%的剩余样本集合中)，因此总体考虑包外估计时，整体考虑的样本肯定大于训练集36.8%的样本个数，但这些样本并不一定是所有$T$个基分类器的包外样本，因此在式(8.20)投票时，针对每个样本$x$不会有$T$票出现($\mathbb{I}(x \notin D_t)$)一般不会$T$次均为真，即“仅考虑那些未使用$x$训练的基学习器在$x$上的预测”。
其中$\mathbb{I}(h_t(x) = y)$表示对$T$个基学习器，每一个都判断结果是否与$y$一致，$y$的取值一般是-1和+1，
如果基学习器结果与$y$一致，则$\mathbb{I}(h_t(x) = y) = 1$，
如果样本不在训练集内，则$\mathbb{I}(x \notin D_t) = 1$，
综合起来看就是，对包外的数据，用“投票法”选择包外估计的结果，即-1或+1。

则Bagging泛化误差的包外估计为

\[\epsilon^{oob} = \frac{1}{|D|}\sum \limits_{(x,y)∈D} \mathbb{I}(H^{oob}(x)\neq y) \quad \quad (8.21) \]

式(8.21)的解释

由式(8.20)可知，$H^{oob}(x)$是对包外数据的估计结果，则该式表示错误的个数除以总的个数，即得到泛化误差的包外估计。本式直接使用将式(8.20)的包外预测结果，直接除以$|D|$(训练集D的样本个数)，也就是说此处假设$T$个基分类器的各自的包外样本的并集一定为训练集Ｄ。

　　事实上，包外样本还有许多其他用途，例如当基学习器是决策树时，可使用包外样本来辅助剪枝，或用于估计决策中各节点的后验概率以辅助对零训练样本节点的处理；当基学习器是神经网络时，可使用包外样本来辅助早期停止以减小过拟合风险。

　　从偏差-方差分解的角度来看，Bagging主要关注降低方差，因此它在不剪枝决策树、神经网络等易受样本扰动的学习器上效用更为明显。

　　我们以基于信息增益划分的决策树为基学习器，在西瓜数据集3.0$\alpha$上运行Bagging算法，不同规模的集成及其基学习器所对应的分类边界如下图所示。

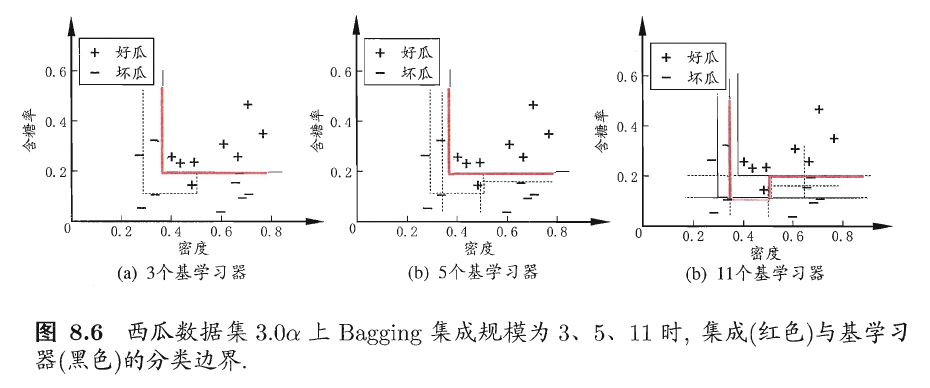
3.2 随机森林(Random Forest)

3.2.1 什么是随机森林?

　　随机森林(Random Forest，简称RF)是Bagging的一个扩展变体。随机森林属于集成学习中的 Bagging（Bootstrap AGgregation 的简称）方法。如果用图来表示他们之间的关系如下：

　　随机森林RF在以决策树为基学习器构建Bagging集成的基础上，进一步在决策树的训练过程中引入了随机属性选择。具体来说，传统决策树在选择划分属性时是在当前节点的属性集合(假定有d个属性)中选择一个最优属性；而在随机森林RF中，对基决策树的每个节点，先从该节点的属性集合中随机选择一个包含$k$个属性的子集，然后再从这个子集中选择一个最优属性用于划分。

　　这里的参数$k$控制了随机性的引入程度：若令$k=d$，则基决策树的构建与传统决策树相同；若令$k=1$，则是随机选择一个属性用于划分；一般情况下，推荐设置$k$的值为$k=log_2d$。

　　随机森林是由很多决策树构成的，不同决策树之间没有关联。
　　当我们进行分类任务时，新的输入样本进入，就让森林中的每一棵决策树分别进行判断和分类，每个决策树会得到一个自己的分类结果，决策树的分类结果中哪一个分类最多，那么随机森林就会把这个结果当做最终的结果。

　　随机森林具有简单、容易实现、计算开销小的特点，令人惊奇的是，它在很多现实任务中展现出强大的性能，被誉为“代表集成学习技术水平的方法”。从算法流程上可以看出，随机森林对Bagging只做了小改动，但是与Bagging中基学习器的“多样性”仅通过样本扰动(通过对初始训练集采样)而来不同，随机森林中基学习器的多样性不仅来自样本扰动，还来自属性扰动，这就使得最终集成的泛化性能可通过个体学习器之间的差异度的增加而进一步提升。

　　随机森林的收敛性与Bagging相似。如下图所示，随机森林的起始性能往往相对较差，特别是在集成中只包含一个基学习器时。这很容易理解，因为通过引入属性扰动，随机森林中个体学习器的性能往往有所降低。然而，随着个体学习器数目的增加，随机森林通常会收敛到更低的泛化误差。

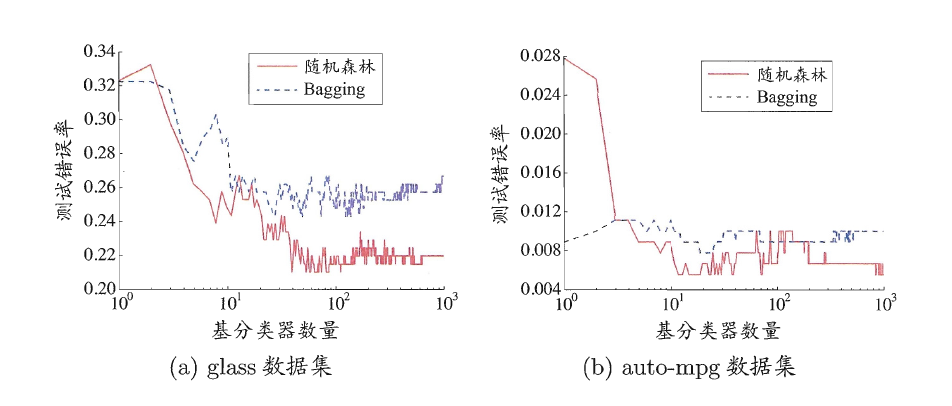
　　值得一提的是，随机森林的训练效率常由于Bagging，因为在个体决策树的构建过程中，Bagging使用的是“确定型”决策树，在选择划分属性时要对节点的所有属性进行考察，而随机森林使用的“随机型”决策树则只需考察一个属性子集。

3.2.2 构造随机森林的4个步骤

一个样本容量为N的样本，有放回的抽取N次，每次抽取1个，最终形成了N个样本。这选择好了的N个样本用来训练一个决策树，作为决策树根节点处的样本。
当每个样本有M个属性时，在决策树的每个节点需要分裂时，随机从这M个属性中选取出m个属性，满足条件m << M。然后从这m个属性中采用某种策略（比如说信息增益）来选择1个属性作为该节点的分裂属性。
决策树形成过程中每个节点都要按照步骤2来分裂（很容易理解，如果下一次该节点选出来的那一个属性是刚刚其父节点分裂时用过的属性，则该节点已经达到了叶子节点，无须继续分裂了）。一直到不能够再分裂为止。注意整个决策树形成过程中没有进行剪枝。
按照步骤1~3建立大量的决策树，这样就构成了随机森林了。

3.2.3 随机森林的优缺点

优点

它可以出来很高维度（特征很多）的数据，并且不用降维，无需做特征选择
它可以判断特征的重要程度
可以判断出不同特征之间的相互影响
不容易过拟合
训练速度比较快，容易做成并行方法
实现起来比较简单
对于不平衡的数据集来说，它可以平衡误差。
如果有很大一部分的特征遗失，仍可以维持准确度。

缺点

随机森林已经被证明在某些噪音较大的分类或回归问题上会过拟合。
对于有不同取值的属性的数据，取值划分较多的属性会对随机森林产生更大的影响，所以随机森林在这种数据上产出的属性权值是不可信的

(四) 结合策略

4.1 为什么要进行学习器结合的原因？

我们将多个学习器结合可能会从以下三个方面带来好处：

一、从统计的角度来看，可降低由于因单学习器可能误选错误的假设而导致泛化性能不佳的风险。
二、从计算的方面来看，可降低学习器陷入糟糕局部极小点的风险。
三、从表示的方面来看，可更逼近真实假设，学到因学习器结合而扩大的假设空间中更好的近似。

下面是学习器结合后带来三个方面好处的直观示意图。

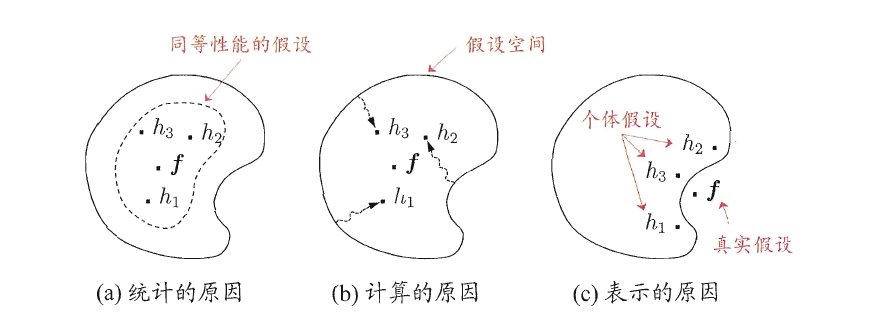
我们分别从以下三个方面来分析为什么要结合学习器的原因：
考虑(a)统计的原因，由于学习任务的假设空间往往很大，因此可能有多个假设在训练集上达到同等性能，此时若使用单学习器可能因误选而导致泛化性能不佳，结合多个学习器则会减小这一风险；

考虑(b)计算的原因，由于学习算法往往会陷入局部极小的情况，其中有的局部极小点所对应的泛化性能可能会很糟糕，而通过多次运行之后进行结合，可降低陷入糟糕局部极小点的风险；

考虑(c)表示的原因，由于某些学习任务的真实假设可能不在当前学习算法所考虑的假设空间中，此时若使用单学习器则肯定无效，而通过结合多个学习器，又由于相应的假设空间有所扩大，有可能学得更好的近似。

4.2 常见的结合策略

我们这里假定集成包含Ｔ个基学习器{$h_1,h_2,...,h_{T}$}，其中$h_i$在示例$x$上的输出为$h_i(x)$。
下面简要介绍几种对基学习器$h_i$进行结合的常见策略。

4.2.1 平均法

　　对数值型输出$h_i(x)∈\mathbb{R}$，最常见的结合策略是使用平均法(averaging)。
针对平均法有以下两种实现方式：

简单平均法(simple averaging)
\[H(x) = \frac{1}{T}\sum \limits_{i=1}^T h_i(x). \quad \quad (8.22) \]

对基分类器的结果进行简单的平均。

加权平均法(weighted averaging)
\[H(x) = \sum \limits_{i=1}^T w_ih_i(x). \quad \quad (8.23) \]

对基分类器的结果进行加权平均

其中$w_i$是个体学习器$h_i$的权重，通常要求$w_i\geq0$,$\sum \limits_{i=1}^T w_i=1$。

显然，简单平均法是加权平均法令$w_i = \frac{1}{T}$的特例。简单平均法在集成学习中具有特别的意义，集成学习中的各种结合方法都可视为其特例或变体。

加权平均法的权重一般是从训练数据中学习而得，然而现实任务中的训练样本通常不充分或存在噪声，这将使得学出的权重不完全可靠。尤其是对规模比较大的集成来说，要学习的权重比较多，较容易导致过拟合。事实上，加权平均法可认为是集成学习研究的基本出发点，对给定的基学习器，不同的集成学习方法可视为通过不同的方式来确定加权平均法中的基学习器权重。

在实验和应用中均显示出，加权平均法未必一定优于简单平均法。一般而言，在个体学习器性能相差较大时宜使用加权平均法，而在个体学习器性能相近时宜使用简单平均法。

4.2.2 投票法

　　对于分类任务来说，学习器$h_i$将从类别标记集合{$c_1,c_2,...,c_N$}中预测出一个标记，最常见的结合策略是使用投票法(voting)。为便于讨论，我们将$h_i$在样本$x$上的预测输出表示出一个Ｎ维向量($h_i^1(x);h_i^2(x);...;h_N^1(x)$)，其中$h_i^j(x)$是$h_i$在类别标记$c_j$上的输出。

针对投票法，有以下三种实现方式：

绝对多数投票法(majority voting)

\[H(x) = \left\{\begin{matrix} c_j, \quad if \sum \limits_{i=1}^T h_i^j(x) > \frac{1}{2} \sum \limits_{k=1}^N \sum \limits_{i=1}^T h_i^k(x); \\ reject, \quad otherwise \end{matrix}\right. \quad \quad (8.24) \]

即若某标记得票过半数，则预测为该标记；否则拒绝预测。

当某个类别$j$的基分类器的结果之和，大于所有结果之和的一半，则选择该类别$j$为最终结果。

相对多数投票法(plurality voting)

\[H(x) = c_{\underset{j}{arg　max} \sum_{i=1}^T h_i^j(x)} \quad \quad (8.25) \]
即预测为得票最多的标记，若同时有多个标记获得最高票，则从中随机选取一个。

相比与其他类别，该类别$j$的基分类器的结果之和最大，则选择类别$j$为最终结果。
加权投票法(weighted voting)

\[H(x) = c_{\underset{j}{arg　max} \sum_{i=1}^T w_ih_i^j(x)} \quad \quad (8.26) \]

相比与其他类别，该类别$j$的基分类器的结果之和最大，则选择类别$j$作为最终结果，与式(8.25)不同的是，该式在基分类器前面乘上一个权重系数，该系数大于等于0，且$T$个权重之和为1。

与加权平均法类似，$w_i$是$h_i$的权重，通常$w_i\geq 0$,$\sum \limits_{i=1}^T w_i = 1$.

　　标准的多数绝对投票法提供了“拒绝预测”选项，这在可靠性要求较高的学习任务是一个很好的机制。但若学习任务要求必须提供预测结果，则绝对多数投票法将退化为相对多数投票法。因此，在不允许拒绝预测的任务中，绝对多数、相对多数投票法统称为“多数投票法”。

　　以上三种方法都没有限制个体学习器输出值的类型。在现实任务中，不同类型个体学习器可能产生不同类型的$h_i^j(x)$值，常见的有：

类标记：$h_i^j(x)∈\left\{0,1\right\}$，若$h_i$将样本$x$预测为类别$c_j$则取值为1，否则为0。
使用类标记的投票亦称“硬投票”(hard voting).
类概率：$h_i^j(x)∈\left[0,1\right]$，相当于对后验概率$P(c_j|x)$的一个估计。
使用类概率的投票亦称“软投票”

需要注意的是，不同类型的$h_i^j(x)$值不能混用。
对一些能在预测出类别标记的同时，产生分类置信度的学习器，其分类置信度可转化为类概率使用。
若此类值未进行规范化，例如支持向量机的分类间隔值，则必须使用一些技术如Platt缩放、等分回归等进行“校准”(calibration)后才能作为类概率使用。有趣的是，虽然分类器估计出的类概率值一般都不太准确。

同时需要注意，若基学习器的类型不太，则类概率值不能直接进行比较；在此种情形下，通常可将类概率输出转化为类标记输出(例如将类概率输出最大的$h_i^j(x)$设为1，其他设为0)，然后再进行投票。

4.2.3 学习法

　　当训练数据很多时，一种更为强大的集合策略是使用“学习法”，即通过另一个学习器来进行结合。

4.2.3.1 Stacking

　　Stacking是学习法的典型代表，这里我们把个体学习器称为初级学习器，用于结合的学习器称为次级学习器或元学习器(meta-learner)。

　　Stacking先从初始数据集训练出初级学习法，然后“生成”一个新数据集用于训练次级学习器。在这个新Ｓ数据集中，初级学习器的输出被当作样例输入特征，而初始样本的标记仍被当作样例标记。

算法Stacking的算法描述

Stacking的算法如下所示，这里我们假定初级学习器使用不同学习算法产生，即初级集成是异质的。

输入：训练集$D=\{(x_1,y_1),(x_2,y_2),\ldots,(x_m,y_m)\}$；
初级学习算法$\mathcal{L}_1,\mathcal{L}_2,\ldots,\mathcal{L}_T$；
次级学习算法$\mathcal{L}$.
过程：
  1: for $t=1,\cdots,T$ do
  2:   $h_t=\mathcal{L}_t(D)$
  3: end for
  4: $D'=\emptyset$
  5: for $i=1,2,\ldots,m$ do
  6:   for $t=1,2,\ldots,T$ do
  7:     $z_{it}=h_t(x_i)$
  8:   end for
  9:   $D'=D' \cup ((z_{i1},z_{i2},\ldots,z_{iT}), y_i)$
  10: end for
  11: $h'=\mathcal{L}(D')$
输出：$H(x)=h'(h_1(x),h_2(x),\ldots,h_T(x))$.

　　在训练阶段，次级训练集是利用初级学习器产生的，若直接用初级学习器的训练集来产生次级训练集合，则过拟合风险会比较大；因此，一般是通过使用交叉验证或留一法这样的方式，用训练初级学习器未使用的样本来产生次级学习器的训练样本。

　　以k折交叉验证为例，初始训练集Ｄ被随机划分为k个大小相似的集合$D_1,D_2,...,D_k$。令$D_j$和$\overline{D}_j$\ $D_j$分别表示第$j$折的测试集和训练集。给定Ｔ个初级学习算法，初级学习器$h_t^{(j)}$通过在$\overline{D}_j$上使用第t个学习算法而得。对$D_j$中每个样本$x_i$，令$z_{it}=h_t^{(j)}(x_i)$，则由$x_i$所产生的次级训练样例的示例部分为$z_{i}=(z_{i1};z_{i2};...;z_{iT})$，标记部分为$y_i$。于是，在整个交叉验证过程结束后，从这T个初级学习器产生的次级训练集是$D'=\left\{(z_{i},y_i)\right\}_{i=1}^m$，然后将$D’$将用于训练次级学习器。

　　次级学习器的输入属性表示和次级学习算法对Stacking集成的泛化性能有很大影响。有研究表明，将初级学习器的输出类概率作为次级学习器的输入属性，用多响应线性回归(Multi-response Linear Regression，简称MLR)作为次级学习算法效果较好，在MLR中使用不同的属性集更佳。｜

4.2.3.1 贝叶斯模型平均BMA

　　贝叶斯模型平均(Bayes Model Averaging，简称BMA)基于后验概率来为不同模型赋予权重，可视为加权平均法的一种特殊实现。对Stacking和BMA进行了比较。理论上来说，若数据生成t模型恰在当前考虑的模型中，且数据噪声很少，则BMA不差于Stacking；然而，在现实应用中无法确保数据生成模型一定在当前考虑的模型中，甚至可能难以用当前考虑的模型来近似，因此，Stacking通常优于BMA，因为其鲁棒性比BMA更好，而且BMA对模型近似误差非常敏感。

(五) 多样性

5.1 误差－分歧分解

　　根据前面的讨论，我们知道，欲构建泛化能力强的集成，个体学习器应“好而不同”。
　　假定我们用个体学习器$h_1,h_2,...,h_T$通过加权平均法$H(x) = \sum \limits_{i=1}^T w_ih_i(x).$结合产生的集成来完成回归学习任务$f:\mathbb{R}^d \longmapsto \mathbb{R}$。

对示例$x$，定义$x$，定义学习器$h_i$的“分歧”为

\[A(h_i|x) = (h_i(x)-H(x))^2 \quad \quad (8.27) \]

该式表示个体学习器结果与预测结果的差值的平方，即为个体学习器的“分歧”。

则集成的“分歧”是

\[\overline{A}(h|x) = \begin{equation*}{\sum}_{i=1}^{T}\end{equation*}w_iA(h_i|x) \\ = \sum_{i=1}^{T}w_i(h_i(x)-H(x))^2 \quad \quad (8.28) \]

该式表示对各个个体学习器的“分歧”加权平均的结果，即集成的“分歧”。

显然，这里的“分歧”项表征了个体学习器在样本$x$上的不一致性，即在一定程度上反映了个体学习器的多样性。个体学习器$h_i$和集成H的平方误差分别为

\[E(h_i|x) = (f(x)-h_i(x))^2 \quad \quad (8.29)\\ \]

该式表示个体学习器与真实值之间差值的平方，即个体学习器的平方误差。

\[E(H|x) = (f(x) - H(X))^2 \quad \quad (8.30) \]

该式表示集成与真实值之间差值的平方，即集成的平方误差。

令$\overline{A}(h|x)=\sum_{i=1}^T w_i\cdot E(h_i|x)$表示个体学习器误差的加权均值，有

\[\overline{A}(h|x) = \sum \limits_{i=1}^T w_iE(h_i|x) - E(H|x) \\ = \overline{E}(h|x) - E(H|x). \quad \quad (8.31) \]

式(8.31)的推导

由式(8.28)可知
　　　　$\overline{A}(h|x) = \sum \limits_{i=1}^T w_i(h_i(x) - H(x))^2 \\ = \sum limits_{i=1}^T w_i(h_i(x)^2 - 2h_i(x)H(x) + H(x)^2) \\ = \sum \limits_{i=1}^T w_ih_i(x)^2 - H(x)^2$
又因为
　　　　$\sum \limits_{i=1}^T w_iE(h_i|x) - E(H|x) \\ = \sum \limits_{i=1}^T w_i(f(x) - h_i(x))^2 - (f(x)-H(x))^2 \\ = \sum \limits_{i=1}^T w_ih_i(x)^2 - H(x)^2$
所以
　　　　$\overline{A}(h|x) = \sum \limits_{i=1}^T w_iE(h_i|x) - E(H|x)$

上式对所有样本$x$均成立，令$p(x)$表示样本的概率密度，则在全样本上有

\[\sum \limits_{i=1}^T w_i \int A(h_i|x)p(x)dx = \sum \limits_{i=1}^T w_i \int E(h_i|x)p(x)dx - \int E(H|x)p(x)dx \quad \quad (8.32) \]

$\int A(h_i|x)p(x)dx$表示个体学习器在全样本上的“分歧”，
$\sum_{i=1}^T w_i \int A(h_i|x)p(x)dx$表示集成在全样本上的“分歧”，然后根据式(8.31)拆成误差的形似。

类似的，个体学习器$h_i$在全样本上的泛化误差和分歧项分别为

\[E_i = \int E(h_i|x)p(x)dx \quad \quad (8.33)\\ \]

表示个体学习器在全样本上的泛化误差。

\[A_i = \int A(h_i|x)p(x)dx \quad \quad (8.34)\\ \]

表示个体学习器在全样本上的分歧。

集成的泛化误差为

\[E = \int E(H|x)p(x)dx \quad \quad (8.35) \]

表示集成在全样本上的泛化误差。

将$E_i$,$A_i$,$E$代入$\sum \limits_{i=1}^T w_i \int A(h_i|x)p(x)dx = \sum \limits_{i=1}^T w_i \int E(h_i|x)p(x)dx - \int E(H|x)p(x)dx$，再令$\overline{E}=\sum_{i=1}^T w_iE_i$表示个体学习器泛化误差的加权均值，$\overline{A}=\sum_{i=1}^T w_iA_i$表示个体学习器的加权分歧值，有

\[E = \overline{E}-\overline{A} \quad \quad (8.36) \]

$\overline{E}$表示个体学习器泛化误差的加权均值，$\overline{A}$表示个体学习器分歧项的加权均值，该式称为“误差-分歧分解”。

上面这个漂亮的式子，明确提示出：个体学习器准确性越高、多样性越大，则集成越好。
上面这个分析首先由[Krogh and Vedelsby,1995]给出，称为“误差－分歧分解”

这里需要注意的是，我们直接将$\overline{E}-\overline{A}$作为优化目标来求解，在现实任务中是很难直接实现的。不仅由于它们是定义在整个样本空间上，还由于$\overline{A}$不是一个可直接操作的多样性度量，它仅在集成构造好之后才能进行估计。此外，还需要注意的是，上面的推导过程只适用于回归学习，难以直接推广到分类学习上去。

5.2 多样性度量

　　顾名思义，多样性度量(diversity measure)是用于度量集成中个体分类器的多样性，即估算个体学习器的多样化程度。典型做法是考虑个体分类器的两两相似/不相似性。
　　给定数据集D＝{$(x_1,y_1),(x_2,y_2),...,(x_m,y_m)$}，对二分类任务，$y_i∈\left\{-1,+1\right\}$，分类器$h_i$与$h_j$的预测结果列联表(contingency table)为

	$h_i=+1$	$h_i=-1$
$h_j=+1$	a	c
$h_j=-1$	b	d

其中，$a$表示$h_i$与$h_j$均预测为正类的样本数目；$b,c,d$含义由此类推；
$a+b+c+d=m$。基于这个列联表，下面给出一些常见的多样性度量。

不合度量(disagreement measure)

\[dis_{ij} = \frac{b+c}{m}　\quad \quad (8.37) \]
$dis_{ij}$的值域为[0,1]。值越大则多样性越大。
相关系数(correlation coefficient)

\[p_{ij} = \frac{ad-bc}{\sqrt{(a+b)(a+c)(c+d)(b+d)}} \quad \quad (8.38) \]
$p_{ij}$为值域为[-1,+1]。若$h_i$和$h_j$无关，则值为0；若$h_i$与$h_j$正相关则值为正，否则为负。
Q-统计量(Q-statistic)

\[Q_{ij} = \frac{ad-bc}{ad+bc} \quad \quad (8.39) \]
$Q_{ij}$与相关系数$p_{ij}$的符号相同，且$|Q_{ij}|\leq|p_{ij}|$.
$\kappa-$统计量($\kappa-$statistic)

\[\kappa = \frac{p_1-p_2}{1-p_2} \quad \quad (8.40) \]
式(8.40)的解释

当$p_1 = p_2$时，$\kappa = 0$；当$p_1 = 1$时，$\kappa = 1$；
一般来说，$p_1 \geq p_2$，即$\kappa \geq 0$，但偶尔也有$p_1 < p_2$的情况，此时$\kappa < 0$。

其中，$p_1$是两个分类器取得一致的概率；$p_2$是两个分类器偶然达到一致的概率，它们可由数据集$D$估算：

\[p_1 = \frac{a+d}{m} \quad \quad (8.41) \\ \]
式(8.41)的解释

分子$a+d$为分类器$h_i$与$h_j$在数据集$D$上预测结果相同的样本数目，分母为数据集$D$总数目，因此$p_1$为两个分类器$h_i$与$h_j$预测结果相同的概率。
若$a + d = m$，即分类器$h_i$与$h_j$对数据集$D$所有样本预测结果均相同，此时$p_1 = 1$。

\[p_2 = \frac{(a+b)(a+c)+(c+d)(b+d)}{m^2} \quad \quad (8.42) \]
式(8.42)的解释

　　将式(8.42)拆分为如下形似，将会很容易理解其含义：
　　　　$p_2 = \frac{a + b}{m} \cdot \frac{a + c}{m} + \frac{c + d}{m} \cdot \frac{b + d}{m}$

　　其中$\frac{a + b}{m}$为分类器$h_i$将样本预测为$+1$的概率，$\frac{a + c}{m}$为分类器$h_j$将样本预测为+1的概率，二者相乘$\frac{a + b}{m} \cdot \frac{a + c}{m}$理解为分类器$h_i$与$h_j$将样本预测为+1的概率；$\frac{c+d}{m}$为分类器$h_i$将样本预测为-1的概率，$\frac{b + d}{m}$为分类器$h_j$将样本预测为-1的概率，二者相乘$\frac{c+d}{m} \cdot \frac{b + d}{m}$可理解为分类器$h_i$与$h_j$将样本预测为-1的概率．

　　这里需要注意下$\frac{a + b}{m} \cdot \frac{a + c}{m}$与$\frac{a}{m}$的不同，$\frac{c + d}{m} \cdot \frac{b + d}{m}$与$\frac{d}{m}$的不同：

　　$\frac{a + b}{m} \cdot \frac{a + c}{m} = p(h_i = +1)p(h_j = +1)$
　　$\frac{a}{m} = p(h_i = +1, h_j = +1)$
　　$\frac{c + d}{m} \cdot \frac{b + d}{m} = p(h_i = -1)p(h_j = -1)$
　　$\frac{d}{m} = p(h_i =-1, h_j = -1)$
即$\frac{a + b}{m} \cdot \frac{c + d}{m} \cdot \frac{b + d}{m}$是分别考虑分类器$h_i$与$h_j$时的概率($h_i$与$h_j$独立)，而$\frac{a}{m}$和$\frac{d}{m}$是同时考虑$h_i$与$h_j$时的概率)(联合概率)。

若分类器$h_i$与$h_j$在D上完全一致，则$\kappa=1$;若它们仅是偶然达成一致，则$\kappa=0$。
$\kappa$通常为非负值，仅在$h_i$与$h_j$达成一致的概率甚至低于偶然性的情况下取负值。

　　以上介绍的都是“成对型”(pairwise)多样性度量，它们可以容易地通过2维图绘制出来。例如著名的“$\kappa-$误差图”，就是将每一对分类器作为图上的一个点，横坐标是这对分类器的$\kappa$值，纵坐标是它们的平均误差，下图给出了一个例子。显然，数据点云的位置越高，则个体分类器准确性越低；点云的位置越靠右，则个体学习器的多样性越小。

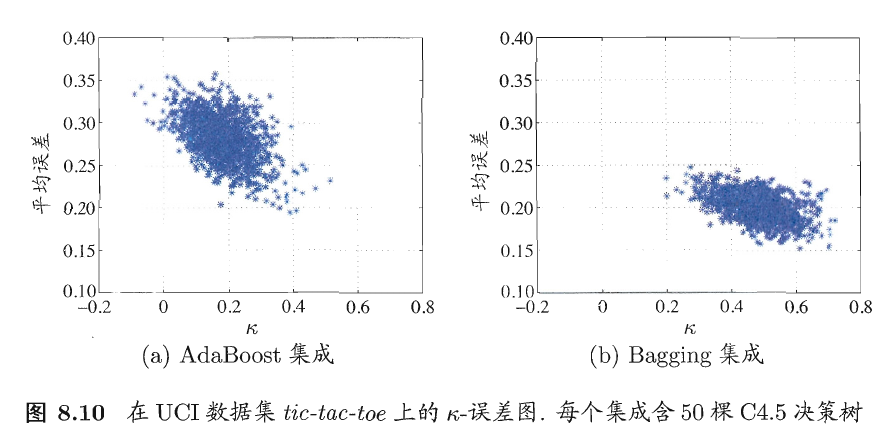
5.3 多样性增强

　　在集成学习中需要有效地生成多样性大的个体学习器。与简单地直接用初始数据训练出个体学习器，如何增强多样性呢？一般思路是在学习过程中引入随机性，常见做法主要是对数据样本、输入属性、输出表示、算法参数进行扰动。

数据样本扰动

　　给定初始数据集，可从中产生出不同的数据子集，再利用不同的数据子集训练出不同的个体学习器。
数据样本扰动通常是基于采样法，例如在Bagging张使用自助采样，在AdaBoost中使用序列采样。此类做法简单高效，使用最广。对很多常见的基学习器，例如决策树、神经网络等，训练样本稍加变化就会导致学习器有显著变动，数据样本扰动法对这样的“不稳定基学习器”很有效；然而，有一些基学习器对数据样本的扰动不敏感，例如线性学习器、支持向量机、朴素贝叶斯、k近似学习器等，这样的基学习器称为稳定基学习器(stable base learner)，对此类基学习器进行集成往往需使用输入属性扰动等其他机制。

输入属性扰动

　　训练样本通常是一组属性描述，不同的“子空间”(subspace，即属性子集)提供了观察数据的不同视角。显然，从不同子空间训练出个体学习器必然有所不同。著名的随机子空间(random subspace)算法就依赖于输入属性扰动，该算法从初始属性集中抽取出若干个属性子集，再基于每个属性子集训练一个基学习器。
　　
　　算法描述如下所示。对包含大量冗余属性的数据，在子空间中训练个体学习器不仅能产生多样性大的个体，还会因属性数的减少而大幅节省时间开销，同时，由于冗余属性多，减少一些属性后训练出的个体学习器也不至于太差。若数据只包含少量属性，或者冗余属性很少，则不宜使用输入属性扰动法。

随机子空间算法描述

输入：训练集D={$(x_1,y_1),(x_2,y_2),...,(x_m,y_m)$};
　　　基学习算法$\mathcal{L}$；
　　　基学习器数T；
　　　子空间属性$d'$;
过程：
1:　for $t=1,2,...,T$ do
2:　　$\mathcal{F}_t=RS(D,d')$
3: 　　$D_t=Map_{\mathcal{F}_t}(D)$
4:　　 $h_t = \mathcal{L}(D_t)$
5:　end for
输出：$H(x)=\underset{y∈\mathcal{Y}}{arg　max}\sum_{t=1}^T\mathbb{I}(h_t(Map_{\mathcal{F}_t}(x))=y)$

输出表示扰动

　此类做法的基本思路是对输出表示进行操纵以增强多样性。可对训练样本的类标记稍作变动，如“翻转”(Flipping Output)随机改变一些训练样本的标记；也可对输出表示进行转化，如“输出调制法”(Output Smearing)将分类输出转化为回归输出后构建个体学习器；还可将原任务拆解为多个可同时求解的子任务，如EOOC法利用纠错输出码将多分类任务拆解为一系列二分类任务来训练基学习器。
算法参数扰动

　　基学习算法一般都有参数需进行设置，例如神经网络的隐层神经元数、初始连接权值等，通过随机设置不同的参数，往往可产生差别较大的个体学习器。例如“负相关法”(Negative Correlation)显式地通过正则化项来强制个体神经网络使用不同的参数。对参数较少的算法，可通过将其学习过程中某些类似方式来替代，从而达到扰动的目的，例如可将决策树使用的属性选择机制替换成其他的属性选择机制。值得指出的是，使用单一学习器时通常需使用交叉验证等方法来确定参数值，这事实上已使用了不同参数训练出多个学习器，只不过最终仅选择其中一个学习器进行使用，而集成学习则相当于把这些学习器都利用起来；由此也可看出，集成学习技术的实际计算开销并不比使用单一学习器大很多。
　
　　不同的多样性增强机制可同时使用，例如随机森林中同时使用了数据样本扰动和输入属性扰动，有些方法甚至同时使用了更多机制。

(六)梯度相关

在集成学习中，梯度提升(Gradient Boosting，GB)、梯度提升树(GB Decision Tree，GBDT)很常见，尤其是近几年非常流行的XGBoost不可忽略，此处单独介绍对比这些概率。

6.1 梯度下降法

设目标函数$f(x)$在$x_k$附近连续可微，且$\nabla f(x_k) = \frac{\nabla f(x)}{\nabla x}\bigg|_{x= x_k} \neq 0$。将$f(x)$在$x_k$处进行一阶$Taylor$展开

\[f(x) \approx f(x_k) + \nabla f(x_k)^T(x - x_k) \]

记$x - x_k = \Delta x$，则上式可写为

\[f(x_k + \Delta x) \approx f(x_k) + \nabla f(x_k)^T \Delta x \]

显然，若$\nabla f(x_k)^T \Delta x < 0$，则有$f(x_k + \Delta x) < f(x_k)$，即相比于$f(x_k)$，自变量增量$\Delta x$会使$f(x)$函数值下降；若要使$f(x) = f(x_k + \Delta x)$下降最快，只要选择$\Delta x$使$\nabla f(x_k)^T \Delta x$最小即可，而此时$\nabla f(x_k)^T \Delta x < 0$，因此使绝对值$|\nabla f(x_k)^T \Delta x|$最大即可。将$\Delta x$分成两部分：$\Delta x = \alpha_k d_k$，其中$d_k$为待求单位向量，$\alpha_k > 0$为待解向量；$d_k$表示往哪个方向改变$x$函数值下降最快，而$\alpha_k$表示沿这个方向的步长。因此，求解$\Delta x$的问题变为

\[(\alpha_k, d_k) = \mathop{\arg\min}_{\alpha,d} \nabla f(x_k)^T \alpha d \]

将以上优化问题分为两步来求解，即

\[d_k = \mathop{\arg\min}_{d} \nabla f(x_k)^T d \quad \text{s.t.}||d||_2 =1 \\ \alpha_k = \mathop{\arg\min}_{\alpha} \nabla f(x_k)^T d_k \alpha \]

以上求解$\alpha_k$的优化问题明显有问题，因为对于$\nabla f(x_k)^T d_k < 0$来说，显然$\alpha_k = +\infty$时取得最小值，求解$\alpha_k$应该求解如下优化问题：

\[\alpha_k = \mathop{\arg\min}_{\alpha} f(x_k + \alpha d_k) \]

对于凸函数来说，以上两步可以得到最优解；但对非凸函数来说，联合求解得到$d_k$和$\alpha_k$，与先求$d_k$然后基于此再求$\alpha_k$的结果应该有时是不同的。
　　由Cauchy-Schwarrtz不等式

\[|\nabla f(x_k)^T d_k| \leq ||\nabla f(x_k)||_2 ||d_k||_2 \]

可知，当且仅当$d_k = -\frac{\nabla f(x_k)}{||\nabla f(x_k)||_2}$时，$\nabla f(x_k)^T d_k$最小，$-\nabla f(x_k)^T d_k$最大。
　　对于$\alpha_k$，若$f(x_k + \alpha d_k)$对$\alpha$的导数存在，则可简单求解如下单变量方程即可：

\[\frac{\partial f(x_k + \alpha d_k)}{\partial \alpha} = 0 \]

下面通过两个例题来帮助理解：

例1：试求$f(x) = x^2$在$x_k = 2$处的梯度方向$d_k$和步长$\alpha_k$。

解：对$f(x)$在$x_k = 2$处进行一阶Taylor展开:

\[f(x) = f(x_k) + f'(x_k)(x - x_k) \\ = x_k^2 + 2x_k(x - x_k) \\ = x_k^2 + 2x_k \alpha d \]

由于此时自变量为一维，因此只有两个方向可以选择，要么正方向，要么反方向。
此时得出$f'(x_k) = 4$，因此$d_k = -\frac{f'(x_k)}{|f'(x_k)|} = -1$。
接下来求$\alpha_k$，将$x_k$和$d_k$代入：

\[f(x_k + \alpha d_k) = f(2 - \alpha) = (2 - \alpha)^2 \]

进而有

\[\frac{\partial f(x_k + \alpha d_k)}{\partial \alpha} = -2(2 - \alpha) \]

令导数等于0，得$\alpha_k = 2$。
则此时

\[\Delta x = \alpha_k d_k = -2 \]

则$x_k + \Delta x = 0$，函数值$f(x_k + \Delta x) = 0$。

例2：试求$f(x) = ||x||_2^2 = x^Tx$在$x_k = [x_k^1,x_k^2]^T = [3,4]^T$处的梯度方向$d_k$和步长$\alpha_k$。

解：对$f(x)$在$x_k = [x_k^1, x_k^2]^T = [3,4]^T$处进行一阶Taylor展开：

\[f(x) = f(x_k) + \nabla f(x_k)^T (x - x_k) \\ = ||x||_2^2 + 2x_k^T(X - X_K) \\ = ||X||_2^2 + 2X_k^T \alpha d \]

此时$\nabla f(x_k) = [6,8]^T$,因此$d_k = - \frac{\nabla f(x_k)}{||\nabla f(x_k)||_2} = [-0.6, -0.8]^T$。
接下来求$\alpha_k$，将$x_k$和$d_k$代入:

\[f(x_k + \alpha d_k) = (3 - 0.6 \alpha)^2 + (4 - 0.8 \alpha)^2 \\ = \alpha^2 - 10 \alpha + 25 \\ = (\alpha -5)^2 \]

因此可得$\alpha_k = 5$(或对$\alpha$求导，再令导数等于0)。此时

\[\Delta x = \alpha_k d_k = [-3, -4]^T \]

则$x_k+\Delta x = [0,0]^T$,函数值$f(x_k+\Delta x) = 0$。

通过以上分析，需要突出强调两点：
(1)梯度下降法求解下降速度最快的方向$d_k$时应该求解如下优化问题：

\[d_k = \mathop{\arg\min}_{d} \nabla f(x_k)^T d \text{s.t.} ||d||_2 = C \]

其中$C$为常量，即不必严格限定$||d_k||_2 = 1$，只要固定向量长度，与$\alpha_k$搭配即可。

(2)梯度下降法求解步长$\alpha_k$应该求解如下优化问题：

\[\alpha_k = \mathop{\arg\min}_{\alpha} f(x_k + \alpha d_k) \]

实际应用中，很多时候不会去求最优的$\alpha_k$，而是靠经验设置一个步长。

6.2 从梯度下降的角度解释AdaBoost

AdaBoost第$t$轮迭代时最小化式(8.5)的指数损失函数

\[\ell_{exp}(H_t|\mathcal{D}) = \mathbb{E}_{x \sim \mathcal{D}}[e^{-f(x)H_t(x)}] = \sum \limits_{x \in D}\mathcal{D}(x)e^{-f(x)H_t(x)} \]

对$\ell_{exp}(H_t|\mathcal{D})$每一项在$H_{t-1}$处泰勒展开

\[\ell_{exp}(H_t|\mathcal{D}) \approx \sum \limits_{x \in D} \mathcal{D}(x) (e^{-f(x)H_{t-1}(x)} - f(x)e^{-f(x)H_{t-1}(x)}(H_t(x) - H_{t-1}(x))) \\ = \sum \limits_{x \in D}\mathcal{D}(E^{-f(x)H_{t-1}(x)} - e^{-f(x)H_{t-1}(x)}f(x)\alpha_t h_t(x)) \\ = \mathbb{E}_{x \sim \mathcal{D}}[e^{-f(x)H_{t-1}(x)} - e^{-f(x)H_{t-1}(x)}f(x)\alpha_th_t(x)] \]

其中$H_t = H_{t-1} + \alpha_t h_t$。注意：$\alpha_t，h_t$是第$t$轮待解的变量。
另外补充以下，在上式展开中的变量为$H_{t}(x)$，在$H_{t-1}$处一阶导数为

\[\frac{\partial e^{-f(x)H_t(x)}}{\partial H_t(x)}\bigg|_{H_t(x) = H_{t-1}(x)} = -f(x)e^{-f(x)H_{t-1}(x)} \]

如果看不习惯上述泰勒展开过程，可令变量$z = H_t(x)$和函数$g(x) = e^{-f(x)z}$，对$g(z)$在$z_0 = H_{t-1}(x)$处泰勒展开，得

\[\begin{align} &g(z) \approx g(z_0) + g'(z_0)(z-z_0) \\ &= g(z_0) - f(x)e^{-f(x)z_0}(z - z_0) \\ &= e^{-f(x)H_{t-1}(x)} - e^{-f(x)H_{t-1}(x)}f(x)(H_t(x) - H_{t-1}(x)) \\ &=e^{-f(x)H_{t-1}(x)} - e^{-f(x)H_{t-1}(x)}f(x)\alpha_t h_t(x) \end{align} \]

注意此处$h_t(x) \in \left\{-1,+1\right\}$，类似于梯度下降法中的约束$||d_k||_2 = 1$。

　　类似于梯度下降法求解下降最快的方向$d_k$，此处先求$h_t$(先不管$\alpha_t$):

\[h_t = \mathop{\arg\min}_{h} \sum \limits_{x \in D}\mathcal{D}(x) (-e^-f(x)H_{t-1}(x))f(x)h(x)) \text{s.t.} h(x) \in \left\{-1, +1 \right\} \]

将负号去掉，最小化变为最大化问题

\[h_t = \mathop{\arg\max}_{h} \sum \limits_{x \in D}\mathcal{D}(x) (e^{-f(x)H_{t-1}(x)}f(x)h(x)) \\ = \mathop{\arg\max}_{h} \mathbb{E}_{x \in \mathcal{D}}[e^{-f(x)H_{t-1}(x)}f(x)h(x)] \quad \text{s.t.} h(x) \in \left\{-1, +1\right\} \]

这就是式(8.14)的第3个等号的结果(其余推导参见8.2节即可)

　　由于这里的$h(x)$约束较强，因此不能直接取负梯度方向，书中经过推导得到了$h_t(x)$的表达式，即式(8.18)。实际上，可以将此结果理解为满足约束条件的最快下降方向。
　　求得$h_t(x)$之后再求$\alpha_t$:

\[\alpha_k = \mathop{\arg\min}_{\alpha} \ell_{exp}(H_{t-1} + \alpha h_t |\mathcal{D}) \]

对指数损失函数$\ell(H_{t-1}+\alpha h_t|\mathcal{D})$求导，得

\[\frac{H_{t-1}+\alpha h_t|\mathcal{D}}{\partial \alpha} = \frac{\partial \left(e^{-\alpha}\sum_{i=1}^{|D|}\mathcal{D}_t'(x_i)+(e^{\alpha}-e^{-\alpha})\sum \limits_{i=1}^{|D|}\mathcal{D}_t'(x_i) \mathbb{I}(f(x_i) \neq h(x_i)) \right)}{\partial \alpha} \\ = -e^{-\alpha} \sum \limits_{i=1}^{|D|}\mathcal{D}_t'(x_i) + (e^{\alpha} + e^{-\alpha})\sum \limits_{i=1}^{|D|}\mathcal{D}_t'(x_i) \mathbb{I}(f(x_i) \neq h(x_i)) \]

令导数等于零，得

\[\frac{e^{-\alpha}}{e^{\alpha} + e^{-\alpha}} = \frac{\sum_{i=1}^{|D|}\mathcal{D}_t'(x_i)\mathbb{I}(f(x_i) \neq h(x_i))}{\sum_{i=1}^{|D|}\mathcal{D}_t'(x_i)} = \sum \limits_{i=1}^{|D|} \frac{\mathcal{D}_t'(x_i)}{Z_t}\mathbb{I}(f(x_i) \neq h(x_i)) \\ = \sum \limits_{i=1}^{|D|}\mathcal{D}_t(x_i)\mathbb{I}(f(x_i) \neq h(x_i)) = \mathbb{E}_{x \sim \mathcal{D}_t}[\mathbb{I}(f(x_i) \neq h(x_i))] \\ = \epsilon_t \]

对上述等式化简，可得

\[\frac{e^{-\alpha}}{e^{\alpha}+e^{-\alpha}} = \frac{1}{e^{2\alpha} + 1} \Rightarrow e^{2\alpha}+1 = \frac{1}{\epsilon_t} \\ \Rightarrow e^{2 \alpha} = \frac{1 - \epsilon_t}{\epsilon_t} \Rightarrow 2\alpha = ln(\frac{1 - \epsilon_t}{\epsilon_t}) \\ \Rightarrow \alpha_t = \frac{1}{2}ln(\frac{1 - \epsilon_t}{\epsilon_t}) \]

即式(8.11)。

通过以上推导可以发现：AdaBoost每一轮的迭代就是基于梯度下降法求解损失函数为指数损失函数的二分类问题(约束条件$h_t(x) \in \left\{-1, +1\right\}$)。

6.3 梯度提升(Gradient Boosting)

　　将AdaBoost的问题一般化，即不限定损失函数为指数损失函数，也不局限于二分类问题，则可以将式(8.5)写为更一般化的形式

\[\ell(H_t|\mathcal{D}) = \mathbb{E}_{x \sim \mathcal{D}}[err(H_t(x), f(x))] \\ = \mathbb{E}_{x \sim \mathcal{D}}[err(H_{t-1}(x) + \alpha_t h_t(x), f(x))] \]

易知，当$f(x) \in \left\{-1, +1 \right\}$且$err(H_t(x), f(x)) = e^{-f(x)H_t(x)}$时，就是式(8.5)。
当时回归问题时，$f(x) \in \mathbb{R}$，损失函数可使用平方损失$err(H_t(x), f(x)) = (H_t(x) - f(x))^2$。

　　针对该一般化的损失函数和一般的学习问题，要通过$T$轮迭代得到学习器

\[H(x) = \sum \limits_{t=1}^T \alpha_t h_t(x) \]

类似于AdaBoost，第$t$轮得到$\alpha_t, h_t(x)$，可先对损失函数在$H_{t-1}(x)$处进行泰勒展开:

\[\ell_{H_t|\mathcal{D}} \approx \mathbb{E}_{x \sim \mathcal{D}} \left[err(H_{t-1}(x), f(x)) + \frac{\partial err(H_t(x), f(x))}{\partial H_t(x)} \bigg|_{H_t(x) = H_{t-1}(x)}(H_t(x) - H_{t-1}(x))\right] \\ = \mathbb{E}_{x \sim \mathcal{D}} \left[err(H_{t-1}(x), f(x)) + \frac{\partial err(H_t(x),f(x))}{\partial H_t(x)}\bigg|_{H_t(x) = H_{t-1}(x)}\alpha_t h_t(x) \right] \\ = \mathbb{E}_{x \sim \mathcal{D}}[err(H_{t-1}(x), f(x))] + \mathbb{E}_{x \sim \mathcal{D}} \left[\frac{\partial err(H_t(x), f(x))}{\partial H_t(x)}\bigg|_{H_t(x) = H_{t-1}(x)} \alpha_t h_t(x) \right] \]

注意，在上式展开中的变量为$H_t(x)$，且有$H_t(x) = H_{t-1}(x) + \alpha_t h_t(x)$(类似于梯度下降法中$x = x_k + \alpha_k d_k$)。上式中括号内第1项为常量$\ell(H_{t-1}|\mathcal{D})$，最小化$\ell(H_t|\mathcal{D})$只须最小化第二项即可。
先不考虑权重$\alpha_t$，求解如下优化问题$h_t(x)$：

\[h_t(x) = \mathop{\arg\min}_{h} \mathbb{E}_{x \sim \mathcal{D}} \left[\frac{\partial err(H_{t}(x), f(x))}{\partial H_t(x)}\bigg|_{H_t(x) = H_{t-1}(x)}h(x) \right] \quad \text{s.t.} \quad constraints \quad for h(x) \]

解得$h_t(x)$之后，再求解如下优化问题可得权重$\alpha_t$：

\[\alpha_t = \mathop{\arg\min}_{\alpha} \mathbb{E}_{x \sim \mathcal{D}}[err(H_{t-1}(x) + \alpha h_t(x), f(x))] \]

以上就是梯度提升(Gradient Boosting)的理论框架，即每轮通过梯度(Gradient)下降的方式将$T$个弱学习提升(Boosting)为强学习器可以看出AdaBoost是其特殊形式。

Gradient Boosting 算法的官方版本参见[Friedman J H. Greedy function approximation: a gradient boosting machine[J]. Annals of statistics, 2001: 1189-1232.]的第 5-6 页(第 1193-1194 页):

\[\begin{align} & ALGORITHM　1(Gradient_Boost) \\ & 1. F_0(x) = \mathop{\arg\min}_{p}\sum_{i=1}^N L(y_i,\rho)　\\ & 2. For \quad m = 1 \quad to \quad M \quad do:\\ & 3. \tilde{y_i} = -[\frac{\partial L(y_i, F(x_i))}{\partial F(x_i)}]_{F(x) = F_{m-1}(x)}，i = 1,N \\ & 4. a_m = \mathop{\arg\min}_{a, \beta}\sum_{i=1}^N L(y_i, F_{m-1}(x_i) + \rho(x_i; a_m)) \\ & 5. \rho_m = \mathop{\arg\min}_{\rho}\sum_{i=1}^N L(y_i, F_{m-1}(x) + \rho h(x_i; a_m)) \\ & 6. F_m(x) = F_{m-1}(x) + \rho_mh(x; a_m) \\ & 7. end \quad For \\ & end \quad Algorithm \end{align} \]

直观地来看，该伪代码针对的还是在任意损失函数$L(y_i, F(x_i))$下的回归问题。
Algorithm 1中第3步和第4不意思是用$\beta h(x_i, a)$拟合$F(x) = F_{m-1}(x)$负梯度，但第4步表示只求参数$a_m$，第5步单独求解参数$\rho_m$，这里的疑问是为什么第4步要用最小二乘法(即3.2节的线性回归)去拟合负梯度(或伪残差)？

　　简单理解如下：第4步要解的$h(x_i,a)$相当于梯度下降法中的待解的下降方向$d$，在梯度下降法中也已提到不必严格限制$||d||_2 = 1$，长度可以由步长$\alpha$调节(例如前面梯度下降解释中的例1，若直接取$d_k = -f'(x_k) = -4$,则可得$\alpha_k = 0.5$，仍有$\Delta x = \alpha_k d_k = -2$)，因此第4步直接用$h(x_i, a)$拟合负梯度，与梯度下降中约束$||d||_2 = 1$的区别在于未对负梯度除以其模值进行归一化而已。

　　那为什么不是直接令$h(x_i, a)$等于负梯度呢?因为这里实际是求假设函数$h$，将数据集中所有的$x_i$经假设函数$h$映射到对应的伪残差(负梯度)$\tilde{y_i}$，所以只能做线性回归了。

　　李航《统计学习方法》第8.4.3节中的算法8.4并未显式体现参数$\rho_m$，这应该是第2步的$(c)$步完成的，因为$(b)$步只是拟合一棵回归树(相当于Algorithm 1第5步解得$rho_m$，只是每个叶节点均对应一个$rho_m$)；而且回归问题中基函数为实值函数，可以将参数$\rho_m$吸收到基函数中。

6.4 梯度提升树

本部分无实质 GBDT 内容,仅为梳理 GBDT 的概念,具体可参考给出的资源链接。
对于 GBDT,一般资料是按 Gradient Boosting+CART 处理回归问题讲解的,如林轩田《机器学习技法》课程第 11 讲(损失函数为平方损失, PPT 中的 C&RT 是 http://pages.stat.wisc.edu/~loh/treeprogs/guide/wires11.pdf的基础版本) :

Gradient Boosted Decision Tree(GBDT)

　　但是,分类问题也可以用回归来处理,例如 3.3 节的对数几率回归,只需将平方损失换
为对率损失(参见式(3.27)和式(6.33),二者关系可参见第 3 章注解中有关式(3.27)的推导)
即可。博客梯度提升树(GBDT)原理小结(https://www.cnblogs.com/pinard/p/6140514.html)从更
一般的角度推导了 GBDT,包括 GBDT 回归版本和分类版本。
特别地,林轩田老师(个人主页:https://www.csie.ntu.edu.tw/~htlin/)的《机器学习基
石》和《机器学习技法》两门课程的主页参见 https://www.csie.ntu.edu.tw/~htlin/mooc/,课程
视频 https://www.bilibili.com/video/av12463015/和 https://www.bilibili.com/video/av12469267/。

6.5 XGBoost

本部分无实质 XGBoost 内容,仅为梳理 XGBoost 的概念,具体可参考给出的资源链接。
首先,XGBoost 是 eXtreme Gradient Boosting 的简称。

其次,XGBoost 与 GBDT 的关系,可大致类比为 LIBSVM 与 SVM(或 SMO 算法)的
关系。LIBSVM 是 SVM 算法的一种高效实现软件包,XGBoost 是 GBDT 的一种高效实现;
在实现层面,LIBSVM 对 SMO 算法进行了许多改进,XGBoost 也对 GBDT 进行了许多改进;
另外,LIBSVM 扩展了许多 SVM 变体,XGBoost 也不再仅仅是标准的 GBDT,也扩展了一
些其它功能。
最后,XGBoost 是由陈天奇(个人主页:https://homes.cs.washington.edu/~tqchen/)开发
的;XGBoost 论文发表在 KDD’16 上,可在 arXiv 下载 https://arxiv.org/abs/1603.02754;
XGBoost 工具包主页 https://xgboost.ai/,文档 https://xgboost.readthedocs.io/en/latest/,源码
 https://github.com/dmlc/xgboost;统计之都(https://cosx.org/)曾对陈天奇做过一个采访,参见
《COS 访谈第 18 期:陈天奇》(https://cosx.org/2015/06/interview-of-tianqi),里面介绍的一
些有关作者的信息是论文中看不到的。

官方文档开篇如是介绍 XGBoost:

GB、 GBDT、 XGBoost 的递进关系简单介绍可参见:一步一步理解 GB、 GBDT、 xgboost
(https://www.cnblogs.com/wxquare/p/5541414.html);另外,有关 XGBoost 介绍,很多人推荐
陈天奇的 PPT:https://homes.cs.washington.edu/~tqchen/pdf/BoostedTree.pdf。

6.6 本章小结

本章内容整体上看并不复杂 , 可以看成是作者的英文专著《 Ensemble Methods:Foundations and Algorithms》 (https://book.douban.com/subject/10494228/,据悉该书中文版即
将由电子工业出版社出版)的精简版,但 8.2 节有关 AdaBoost 的推导感觉很难吃透,尤其是本节还涉及到如 Gradient Boosting、GBDT、XGBoost 等概念,因此必须读一些原始文献和其它参考资料方能对此有所理解,下面对这些概念进行一个简单的梳理。
提升(Boosting)是一族可将弱学习提升为强学习器的算法,弱学习器间存在强依赖关系、
必须串行生成。这族算法的工作机制类似:先从初始训练集训练出一个基学习器,再根据基学习器的表现对训练样本分布进行调整,使得先前基学习器做错的训练样本在后续受到更多关注,然后基于调整后打着本分布来训练下一个基学习器;如此重复进行,直至基学习器数目达到事先指定的值 T,最终将这 T 个基学习器进行加权结合。(摘自西瓜书 P173)
提升树(Boosting Tree)是以决策树为基学习器的提升方法(i.e.,Boosting+ Decision Tree)。
对分类问题决策树是二叉分类树,对回归问题决策树是二叉回归树。
(李航《统计学习方法》 )
梯度提升(Gradient Boosting)是基于加法模型和前向分步算法一种理论框架,并不限定损失函数,也不限定基分类器的类型(类型包含两层含义:第 1 层如分类和回归等;第 2层如决策树、SVM、神经网络等)。
梯度提升树(GBDT) = Gradient Boosting + Decision Tree (CART),这里 CART 取为回归树。李航《统计学习方法》第 8.4.3 节中的算法 8.4 实际为 GBDT 算法,与刘建平 Pinard 博客《梯度提升树(GBDT)原理小结》介绍基本一致,林轩田《机器学习技法》课程第 11 讲则特指损失函数为平方损失。

特别地,8.2 节介绍的 AdaBoost(Adaptive Boosting)是当 Gradient Boosting 中损失函数为指数损失函数、基分类器为二分类(只能取+1 和-1 两个值)时的特殊形式(i.e., Gradient Boosting + Exponential Loss + Binary base classifier),这里基分类器可以为任何二分类器,如决策树、SVM、神经网络等。当然,西瓜书作者在第 190 页的阅读材料中提到,这仅是源“统计视角”的一种推导而已,但这派理论产生的推论并不能解释某些现象,因此这可能仅是一个与 AdaBoost 相似的学习过程而非 AdaBoost 本身。
当 AdaBoost 的基分类器为二分类决策树时,也可以称为提升树,
“对二类分类问题,提升树算法只需将 AdaBoost 算法 8.1 中的基本分类器限制为二类分类树即可,可以说这时的
提升树是 AdaBoost 算法的特殊情况”。但这里与 GBDT 不一样,因为

AdaBoost 限定了基分类器为二分类(实际上也可以做回归任务),并不像 GBDT 里那样,每轮迭代与残差(负梯度)拟合;而且已经提到,GBDT 一般特指 Gradient Boosting 与 CART 回归树的结合。

XGBoost 是 GBDT 的一个软件包,类似于 LIBSVM 是 SVM 的一个软件包。XGBoost在实现 GBDT 时进行了一些细节上的改进和扩展。
各种概念之间的包含关系如下图所示:

以上仅为个人的初步理解,可能有误,勿被误导^_

参考材料:
[1] 周志华《机器学习》
[2] 李航《统计学习方法》
[3] 邱锡鹏《神经网络与深度学习》
[4] Adaboost 算法
[5] 一文看懂集成学习（详解 bagging、boosting 以及他们的 4 点区别）
[6] 机器学习数学原理（8）——霍夫丁不等式

posted @ 2021-04-27 17:59 Xu_Lin 阅读(460) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

	\(h_i=+1\)	\(h_i=-1\)
\(h_j=+1\)	a	c
\(h_j=-1\)	b	d

Xu_Lin

Do more; Learn more; Be more

机器学习-集成学习