机器学习-支持向量机

机器学习—支持向量机

支持向量机：
(一)间隔与支持向量
(二)软间隔与正则化
(三)核方法

(零)前置知识

0 基本概念

0.1 线性可分

　　给定一个数据集Ｔ = {($x_1,y_2$),($x_2,y_2$),...,($x_N,x_N$)}
　　其中，$x_i∈\mathcal{X}=R^n$，$y_i∈\mathcal{Y}＝\left\{+1,-1\right\},i=1,2,...,N$，如果存在某个超平面$S$

\[w \cdot x + b = 0 \]

　　能够将数据集的正实例点和负实例点完全正确地划分到超平面的两侧，即对所有$y_i = +1$的实例$i$，有$w\cdot x_i+b>0$，对所有$y_i＝-1$的实例$i$，有$w \cdot x_i+b<0$，则称数据集Ｔ为线性可分数据集(linearly separable data set)；否则，称数据集Ｔ线性不可分。

0.2 向量和向量空间

0.2.1 向量

标量(Scalar)是一个实数，只有大小，没有方向。标量一般用斜体小写英文字母$a,b,c$来表示。
向量(Vector)是由一组实数组成的有序数组，同时具有大小和方向。
一个N维向量$\alpha$是由Ｎ个有序实数组成，表示为

\[\alpha = [a_1,a_2,...,a_N] \]

其中$a_n$称为向量$\alpha$的第n个分量，或第n维。向量符号一般用黑斜体小写英文字母，或小写希腊字母$\alpha,\beta,\gamma$等来表示。

0.2.2 向量空间

向量空间(Vector Space)，也称线性空间(Linear Space)，是指由向量组成的集合，并满足以下两个条件：
(1)向量加法($+$): 向量空间$\mathcal{V}$中的两个向量$a$和$b$，它们的和$a+b$也属于空间$\mathcal{V}$。
(2)向量乘法($\cdot$): 向量空间$\mathcal{V}$中的任一向量$\alpha$和任一标量$c$，它们的乘积$c\cdot\alpha$也属于空间$\mathcal{V}$。

欧式空间
一个常见的线性空间是欧式空间(Euclidean Space)。一个欧式空间通常为$\mathbb{R}^N$，其中Ｎ为空间维度(Dimension)。欧式空间中的向量加法和标量乘法分别定义为：

\[向量加法 [a_1,a_2,...,a_N]+[b_1,b_2,...,b_N]＝[a_1+b_1,a_2+b_2,...,a_N＋b_N], \\ 标量乘法 c\quad \cdot[a_1,a_2,...,a_N] = [ca_1,ca_2,...,ca_N] \]

其中$a,b,c∈\mathbb{R}$为标量。

线性子空间
向量空间$\mathcal{V}$的线性子空间$\mathcal{U}$是$\mathcal{V}$的一个子集，并且满足向量空间的条件(向量加法和标量乘法)。

线性无关
线性空间$\mathcal{V}$中的M个向量{$v_1,v_2,...,v_M$}，如果对任意的一组标量$\lambda_1,\lambda_2,...,\lambda_M$，满足$\lambda_1v_1+\lambda_2v_2+...+\lambda_Mv_M$，则必然$\lambda_1=\lambda_2=...=\lambda_M=0$，那么{$v_1,v_2,...,v_M$}是线性无关的，也称为线性独立的。

基向量
Ｎ维向量空间$\mathcal{V}$的基(Base)$\mathcal{B}$={$e_1,e_2,...,e_N$}是$\mathcal{V}$的有限子集，其元素之间线性无关。向量空间$\mathcal{V}$中所有的向量都可以按唯一的方式表达为$\mathcal{B}$中的向量的线性组合。对任意$v∈\mathcal{V}$，存在一组标量$(\lambda_1,\lambda_2,...,\lambda_N)$使得

\[v = \lambda_1e_1+\lambda_2e_2+...+\lambda_Ne_N \]

其中基$\mathcal{B}$中的向量称为基向量(Base Vector)。如果基向量是有序的，则标量($\lambda_1,\lambda_2,...,\lambda_N$)称为向量$v$关于基$\mathcal{B}$的坐标(Coordinate)。

Ｎ维空间$\mathcal{V}$的一组标准基(Standard Basis)为

\[e_1 = [1,0,0,...,0], \\ e_2 = [0,1,0,...,0], \\ ... \\ e_3 = [0,0,0,...,1] \]

$\mathcal{V}$中的任一向量$v=[v_1,v_2,...,v_N]$可以唯一地表示为

\[[v_1,v_2,...,v_N] = v_1e_1 + v_2e_2 + \cdots + v_Ne_N \]

$v_1,v_2,...,v_N$也称为向量$v$的笛卡尔坐标(Cartesian Coordinate)。
向量空间中的每个向量都可以看作一个线性空间中的笛卡尔坐标。

内积
一个Ｎ维线性空间中的两个向量$a$和$b$，其内积(Inner Product)为

\[\left \langle a,b \right \rangle = \sum \limits_{n=1}^N a_nb_n \]

内积也称为点积(Dot Product)或标量积(Scalar Product)。

正交
如果向量空间中两个向量的内积为0，则它们正交(Orthogonal)。
如果向量空间中一个向量$v$与子空间$\mathcal{U}$中每个向量都正交，那么向量$v$和子空间$\mathcal{U}$正交。

0.2.3 范数

范数(Norm)是一个表示向量“长度”的函数，为向量空间内的所有向量赋予非零的正长度或大小。对于一个Ｎ维向量$v$，一个常见的范数函数为$\ell_{P}$范数。

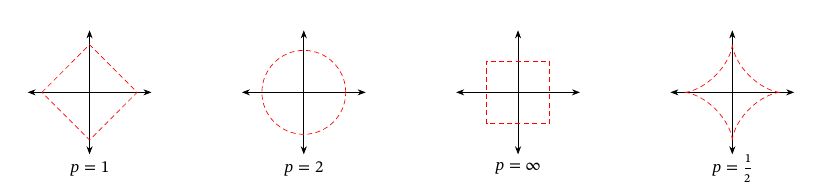
\[\ell_{P}(v) = ||v||_{P} = \left(\sum \limits_{n=1}^N |v_n|^p\right)^{\frac{1}{p}} \]

其中$p\geq 0$为一个标量的参数。常用的$p$的取值为$1,2,\infty$等。

$\ell_1$范数
$\ell_1$范数为向量的各个元素的绝对值之和。

\[||v||_1 = \sum \limits_{n=1}^N |v_n| \]

$\ell_2$范数
$\ell_2$为向量的各个元素的平方和再开平方。

\[||v||_2 = \sqrt{\sum \limits_{n=1}^N v_n^2} = \sqrt{v^Tv} \]

$\ell_2$范数又称为Euclidean 范数或Frobenius范数。从几何角度，向量也可以表示从原点出发的一个带箭头的有向线段，其$\ell_2$范数为线段的长度，也常称为向量的模。

$\ell_{\infty}$范数
$\ell_{\infty}$范数为向量的各个元素的最大绝对值，

\[||v||_{\infty} = max \left\{v_1, \right\} \]

下图给出了常见范数的示例，其中红线表示不同范数的$\ell_P=1$的点。

0.2.4 常见的向量

全0向量
全0向量是指所有元素都为0的向量,用$0$表示。全0向量为笛卡尔坐标系中的原点。

全1向量
全1向量是指所有元素都为1的向量,用$1$表示。

$one-hot向量$
$one-hot向量$为有且只有一个元素为1，其余元素都为0的向量。$ont-hot$向量是在数字电路中的一种状态编码，指对任意给定的状态，状态寄存器中只有1位为1，其余位都为0。

0.3 矩阵

0.3.1 线性映射

线性映射(Linear Mapping)是指从线性空间$\mathcal{X}$到线性空间$\mathcal{Y}$的一个映射函数：$f:\mathcal{X}\to \mathcal{Y}$，并满足:对于$\mathcal{X}$中任何两个向量$u$和$v$以及任何标量$c$，有

\[f(u+v) = f(u) + f(v) , \\ f(cv) = cf(v) \]

两个有限维欧式空间的映射函数:$f:\mathbb{R^N}\to\mathbb{R^M}$可以表示为

\[y = Ax \overset{\Delta}= \begin{bmatrix} a_{11}x_1& a_{12}x_2& \cdots & a_{1N}x_N\\ a_{21}x_1& a_{22}x_2& \cdots & a_{2N}x_N\\ \vdots & \vdots & \ddots & \vdots \\ a_{M1}x_1& a_{M2}x_2& \cdots & a_{MN}x_N \end{bmatrix} \]

其中Ａ是一个由Ｍ行Ｎ列个元素排列成的矩形阵列，称为$M×N的矩阵(Matrix)：

\[A = \begin{bmatrix} a_{11}& a_{12}& \cdots & a_{1N}\\ a_{21}& a_{22}& \cdots & a_{2N}\\ \vdots & \vdots & \ddots & \vdots \\ a_{M1}& a_{M2}& \cdots & a_{MN} \end{bmatrix} \]

向量$x∈\mathbb{R}^N$和$y∈\mathbb{R}^N$为两个空间中的向量。$x$和$y$可以分别表示为$N×1$的矩阵和$M×1$的矩阵。

\[x = \begin{bmatrix} x_1\\ x_2\\ \vdots\\ x_N \end{bmatrix},\quad y = \begin{bmatrix} y_1\\ y_2\\ \vdots\\ y_M \end{bmatrix} \]

这种表示形式称为列向量，即为只有一列的向量。
很多书为简化书写、方便排版起见，约定行向量(即1×1的矩阵)用逗号隔离的向量[$x_1,x_2,...,x_N$]表示；
列向量用分号隔开的向量$[x_1;x_2;...;x_N]$表示，或用行向量的转置$[x_1,x_2,...,x_N]^T$表示。

矩阵$A∈\mathbb{R}^{Ｍ×N}$定义了一个从空间$\mathbb{R}^N$的线性映射。一个矩阵Ａ从左上角数起的第m行第n列上的元素称为第m,n项，通常记为$[A]_{mn}或a_{mn}$。

0.3.2 特征值与特征向量

　　对一个$N×N$的矩阵Ａ,如果存在一个标量$\lambda$和一个非零向量$v$满足

\[Av = \lambda v \]

则$\lambda$和$v$分别称为矩阵Ａ的特征值(Eigenvalue)和特征向量(Eigenvector)。
　　当用矩阵Ａ对它的特征向量$v$进行线性映射时，得到的新向量只是在$v$的长度上缩放$\lambda$倍。给定一个矩阵的特征值，其对应的特征向量的数量是无限多的。令$u$和$v$是矩阵Ａ的特征值$\lambda$对应的特征向量，则$\alpha u$和$u＋v$也是特征值$\lambda$对应的特征向量。
　　如果矩阵Ａ是一个$N×N$的实对称矩阵，则存在实数$\lambda_1,\lambda_2,...,\lambda_N$，以及Ｎ个互相正交的单位向量$v_1,...,v_N$，使得$v_n$为矩阵Ａ的特征值为$\lambda_n$的特征向量($1 \leq n \leq N$)。

0.3.3 特征空间

所有特征向量存在的空间。每个具体的输入是一个实例，通常由特征向量表示。
例如：输入实例$x$的特征向量记作

\[x = (x^{(1)},x^{(2)},...,x^{(n)})^{T} \]

其中，$x_i$表示$x$的第$i$个特征向量，通常用$x_i$表示多个输入变量中的第i个,多个这样的特征向量组成的空间就叫特征空间。

0.3.4 正定矩阵

如果一个$N×N$的对称矩阵Ａ，如果对于所有的非零向量$x∈\mathbb{R}^n$都满足

\[x^TAx > 0 \]

则$A$为正定矩阵(Positive-Definite Matrix)。如果$x^TAx\geq0$，则A是半正定矩阵(Positive-Semidefinite Matrix)。

0.3.5 稀疏矩阵与稠密矩阵

在矩阵中，若数值为0的元素数目远远多于非0元素的数目，并且非0元素分布没有规律时，则称该矩阵为稀疏矩阵；与之相反，若非0元素数目占大多数时，则称该矩阵为稠密矩阵。定义非零元素的总数比上矩阵所有元素的总数为矩阵的稠密度

0.3.6 类内散度矩阵(散布矩阵)

类内散度矩阵用于表示样本点围绕均值的散布情况，其定义如下：
设有M个类别($\Omega_i,...,\Omega_M$)，$\Omega_i$类样本集$\left\{X_1^{(i)},X_2^{(i)},...,X_N^{(i)} \right\}$,
$\Omega_i$类的散度矩阵定义为：

\[S_w^{(i)} = \frac{1}{N_i} \sum \limits_{k=1}^{N_i} \left(X_k^{(i)} -m^{(i)}\right)\left(X_k^{(i)} -m^{(i)}\right)^T \]

其中，$S_w^{(i)}$即是类$\Omega_i$的协方差矩阵。
总的类内散度矩阵为：

\[S_W = \sum \limits_{i=1}^M P(\Omega_i)S_w^{(i)} = \sum \limits_{i=1}^M P(\Omega_i)\frac{1}{N_i}\sum \limits_{k=1}^{N_i}\left(X_k^{(i)} -m^{(i)}\right)\left(X_k^{(i)} -m^{(i)}\right)^T \]

则：迹{$S_ｗ$}是所有类的特征方差的平均测度。
关于特征选择和提取的结果，类内散步矩阵的积越小越好。

从形式上看就是求的方差最小化，比如我们有一纬数据，如果方差太大肯定数据距离中心点非常分散拉，我们让方差最小化的目的就是希望每个数据距离均值更近，表现出来就是数据很紧凑。

0.4 间隔的定义

　　在特征空间中，常用的间隔定义有两种，一种称之为函数间隔，一种为几何间隔。

0.4.1 函数间隔

　　对于给定的训练数据集$D$和超平面$(w,b)$，定义超平面$(w,b)$关于样本点$(x_i,y_i)$的函数间隔为

\[\hat \gamma_i = y_i(w\cdot x_i+b) \]

　　定义超平面$(w,b)$关于训练数据集$D$的函数间隔为超平面$(w,b)$关于$D$中所有样本点$(x_i,y_i)$的函数间隔之最小值，即

\[\hat \gamma = \underset{i=1,...,N}{min} \hat \gamma_i \]

　　函数间隔表示分类预测的正确性及确信度。但是选择分离超平面时，只有函数间隔还不够。因为只要成比例地改变$w$和$b$，例如将其该为$2w$和$2b$，事实上超平面并没有改变，但函数间隔却成为原来的2倍。
　　这一事实启示我们，可以对分离超平面的法向量$w$加以某些约束，如规范化，$||w||=1$，使得间隔是确定的。

0.4.2 几何间隔

　　对于给定的训练数据集$D$和超平面$(w,b)$，定义超平面$(w,b)$关于样本点$(x_i,y_i)$的几何间隔为

\[\gamma_i = y_i \left(\frac{w}{||w||}\cdot x_i + \frac{b}{||w||} \right) \]

　　定义超平面$(w,b)$关于训练数据集$D$的几何间隔为超平面$(w,b)$关于$D$中所有样本点$(x_i,y_i)$的几何间隔之最小值，即

\[\gamma = \underset{i=1,...,N}{min} \gamma_i \]

　　超平面$(w,b)$关于样本点$(x_i,y_i)$的几何间隔一般是实例点到超平面的带符号的距离(signed distance)，当样本点被超平面正确分类时就是实例点到超平面的距离。

　　从函数间隔和几何间隔的定义可知，函数间隔和几何间隔有下面的关系

\[\gamma_i = \frac{\hat \gamma_i}{||w||} \\\gamma = \frac{\hat \gamma}{||w||} \]

　　由此易知，如果$||w||=1$，那么这时函数间隔与几何间隔相等。如果超平面参数$w$和$b$成比例地改变(超平面没有改变)，函数间隔也按此比例改变，而几何间隔不变。

0.5 凸优化问题

凸优化问题是指约束最优化问题

\[\underset{w}{min} f(w)　\\ \text{s.t}.　g_i(w)≤0, \quad i=1,2,...,k \\ h_i(w)=0, \quad i=1,2,...,l \]

其中，目标函数$f(w)$和约束函数$g_i(w)$都是$R^n$上的连续可微的凸函数，约束函数$h_i(w)$是$R^n$上的仿射函数。
当目标函数$f(w)$是二次函数且约束函数$g_i(w)$是仿射函数时，上述凸最优化问题称为凸二次规划问题。

0.6拉格朗日对偶型

0.6.1 原始问题

假设$f(x),c_i(x),h_j(x)$是定义在$Ｒ^n$上的连续可微函数。考虑约束最优化问题

\[\underset{x∈R^n}{min} f(x) \\ \text{s.t} c_i(x) ≤ 0, \quad i = 1,2,...,k \\ h_j(x) = 0, \quad j = 1,2,...,l \]

称此约束最优化问题为原始最优化问题或原始问题。

　　首先，引进广义拉格朗日函数(generalized Lagrange function)

\[L(x,\alpha,\beta) = f(x) + \sum \limits_{i=1}^k \alpha_i c_i(x) + \sum \limits_{j=1}^l \beta_j h_j(x) \]

　　这里，$x=(x^{(1)},x^{(2)},...,x^{(n)})∈R^n$,$\alpha_i,\beta_j$是拉格朗日乘子，$\alpha_i≥0$。
考虑$x$的函数：

\[\theta_P(x) = \underset{\alpha,\beta:\alpha_i≥0}{max}L(x,\alpha,\beta) \]

这里，下标P表示原始问题。

　　假设给定某个$x$。如果$x$违反原始问题的约束条件，即存在某个$i$使得$c_i(x)>0$或者存在某个$j$使得$h_j(x)≠0$,那么就有

\[\theta_P(x) = \underset{\alpha,\beta:\alpha_i≥0}{max}\left[f(x) + \sum \limits_{i=1}^k \alpha_i c_i(x) + \sum \limits_{j=1}^l \beta_j h_j(x) \right] = +\infty \]

　　因为若某个$i$使得约束$c_i(x)>0$，则可令$\alpha_i \to\infty$，若某个$j$使$h_j(x)≠0$,则可令$\beta_j$使$\beta_jh_j(x) \to +\infty$,而将其余各$\alpha_i,\beta_j$均取为0。
　　
　　相反地，如果$x$满足约束条件式$\text{s.t} c_i(x) ≤ 0, \quad i = 1,2,...,k$和$h_j(x) = 0, \quad j = 1,2,...,l$,则由$\theta_P(x) = \underset{\alpha,\beta:\alpha_i≥0}{max}\left[f(x) + \sum \limits_{i=1}^k \alpha_i c_i(x) + \sum \limits_{j=1}^l \beta_j h_j(x) \right] = +\infty$和$\theta_P(x) = \underset{\alpha,\beta:\alpha_i≥0}{max}L(x,\alpha,\beta)$可知，

\[\theta_P(x) = f(x) \]

　　因此

\[\theta_P(x) = \left\{\begin{matrix} f(x), \quad x满足原始问题约束\\ +\infty,　　　　　　　　　其他 \\ \end{matrix}\right. \]

　　所以，如果考虑极小化问题

\[\underset{x}{min}\theta_P(x) = \underset{x}{min} \underset{\alpha,\beta:\alpha_i≥0}{max}L(x,\alpha, \beta) \]

它是与原始最优化问题等价的，即它们有相同的解。问题$\underset{x}{min} \underset{\alpha,\beta:\alpha_i≥0}{max}L(x,\alpha, \beta)$称为广义拉格朗日函数的极大极小问题。这样一来，就把原始最优化问题表示为广义拉格朗日函数的极小极大问题。
为了方便，定义原始问题的最优值$p^* = \underset{x}{min} \theta_P(x)$称为原始问题的解。

0.6.2 对偶问题

定义

\[\theta_D(\alpha, \beta) = \underset{x}{min}L(x,\alpha,\beta) \]

再考虑极大化$\theta_D(\alpha,\beta) = \underset{x}{min}L(x,\alpha,\beta)$，即

\[\underset{\alpha,\beta;\alpha_i≥0}{max}\theta_D(\alpha, \beta) = \underset{\alpha,\beta;\alpha_i≥0}{max} \underset{x}{min} L(x,\alpha,\beta) \]

则问题$\underset{\alpha,\beta;\alpha_i≥0}{max} \underset{x}{min} L(x,\alpha,\beta)$称为广义拉格朗日函数的极大极小问题。
可以向广义拉格朗日函数的极大极小问题表示为约束最优化问题：

\[\underset{\alpha,\beta}{max} \theta_D(\alpha,\beta) = \underset{\alpha, \beta}{max} \underset{x}{min}L(x,\alpha,\beta) \\ \text{s.t}　\alpha_i≥0, \quad i=1,2,...,k \]

称为原始问题的对偶问题。

定义对偶问题的最优值

\[d^* = \underset{\alpha,\beta:\alpha_i≥0}{max}\theta_D(\alpha,\beta) \]

称为对偶问题的值。

拉格朗日对偶问题(Lagrangian Dual Problem)为

\[\max_{\lambda,\mu} \varGamma(\lambda, \mu), s.t. \mu \succeq 0 \]

其中$\varGamma(\lambda, \mu)$为$L(x, \lambda, \mu)$的下确界(infimum)，即

\[\varGamma(\lambda, \mu) = \inf_xL(x, \lambda, \mu) \]

如何求$\varGamma(\lambda, \mu)$的表达式呢?我们令$\frac{\partial L(x, \lambda,\mu)}{\partial x} = 0$，将$x$用$\lambda,\mu$表示代入$L(x,\lambda,\mu)$即可。
设待求解目标：$\min_x f(x),s.t. h(x) = 0, g(x) \leq 0$
① 拉格朗日函数$L(x, \lambda, \mu) = f(x) + \lambda h(x) + \mu g(x)$.
② 令$\frac{\partial L(x, \lambda,\mu)}{\partial x} = 0$，解得用$\lambda,\mu$表示的$x$.
③ 将$x$代入$L(x,\lambda,\mu)$得：$\varGamma(\lambda,\mu) = \min_xL(x,\lambda,\mu)$.
④ 对偶问题：$\max_{\lambda,\mu}\varGamma(\lambda,\mu), s.t. \mu \succeq 0$.

3.原始问题和对偶问题的关系

下面讨论原始问题和对偶问题的关系，这里有几个定理(不设证明)
Th1若原始问题和对偶问题都有最优值，则

\[d^* = \underset{\alpha,\beta:\alpha_i≥0}{max} \underset{x}{min} L(x,\alpha,\beta) ≤ \underset{x}{min} \underset{\alpha,\beta:\alpha_i≥0}{max} L(x,\alpha,\beta) = p^* \]

Th1 推论设$x^*$和$\alpha^*$,$\beta^*$分别是原始问题和对偶问题的可行解，并且$d^* = p^*$，则$x^*$和$\alpha^*$，$\beta^*$分别是原始问题和对偶问题的最优解。

Th2 考虑原始问题和对偶问题。假设函数$f(x)$和$c_i(x)$是凸函数，$h_j(x)$是仿射函数；并且假设不等式约束$c_i(x)$是严格可行的，即存在$x$，对所有$i$有$c_i(x)<0$，则存在$x^*,\alpha^*,\beta^*$，使$x^*$是原始问题的解，$\alpha^*,\beta^*$是对偶问题的解，并且

\[p^* = d^* = L(x^*, \alpha^*, \beta^*) \]

Th3 对原始问题和对偶问题，假设函数$f(x)$和$c_i(x)$是凸函数，$h_j(x)$是仿射函数，并且不等式约束$c_i(x)$是严格可行的，则$x^*$和$\alpha^*,\beta^*$分别是原始问题和对偶问题的解的充分必要条件是$x^*,\alpha^*,\beta^*$满足下面的Karush-Kuhn-Tuchker(KKT)条件：

\[\nabla_xL(x^*,\alpha^*, \beta^*) = 0 \\\alpha_i^*c_i(x^*) = 0, \quad i = 1,2,...,k \\c_i(x^*) ≤ 0, \quad i = 1,2,...,k \\\alpha_i^* ≥ 0, \quad i = 1,2,...,k \\h_j(x)^* = 0,\quad j = 1,2,...,l \]

其中，$\alpha_i^*c_i(x^*) = 0, \quad i = 1,2,...,k$称为KKT的对偶互补条件。由此条件可知：若$\alpha_i^*>0$则$c_i(x^*)=0$.

支持向量机简述

　　支持向量机(support vector machines,SVM)是一种二类分类模型.它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别与感知机；支持向量机还包括核心技巧，这使得它称为实质上的非线性分类器。支持向量机的学习策略就是间隔最大化，可形式化为一个求解凸二次规划(convex quadratic programming)的问题，也等价于正则化的合页损失函数的最小化问题。支持向量机的学习算法是求解凸二次规划的最优化算法。

　　支持向量机学习方法包含构建由简至繁的模型：
线性可分支持向量机(linear support vector machine in linearly separable case)、线性支持向量机(non-linear support vector machine)。简单模型是复杂模型的基础，也是复杂模型的特殊情况。

当训练数据线性可分时，通过硬间隔最大化(hard margin maximization)，学习一个线性的分类器，即线性可分支持向量机(soft margin maximization)，又称为硬间隔支持向量机；
当训练数据近似线性可分时，通过软间隔最大化(soft margin maximization)，也学习一个线性的分类器，即线性支持向量机，又称为软间隔支持向量机；
当训练数据线性不可分时，通过核技巧(kernel trick)及软间隔最大化，学习非线性支持向量机。

　　当输入空间为欧式空间或离散集合、特征空间为希尔伯特空间时，核函数(kernel function)表示将书从输入空间映射到特征空间得到的特征向量之间的内积的内积。通过使用核函数可以学习非线性支持向量机，等价于隐式地在高维的特征空间中学习线性支持向量机。这样的方法称为核技巧。核方法(kernel method)是比支持向量机更为一般的机器学习方法。　　

(一)间隔与支持向量

　　考虑一个二分类学习问题。假设输入空间与特征空间为两个不同的空间。输入空间为欧氏空间或离散集合，特征空间为欧氏空间或希尔伯特空间。线性可分支持向量机、线性支持向量机假设这两个空间的元素一一对应，并将输入空间中的输入映射为特征空间中的特征向量。非线性支持向量机利用一个从输入空间到特征空间的非线性映射将输入映射为特征向量。所以，输入都有输入空间转换到特征空间，支持向量机的学习是在特征空间进行的。

　　假设给定一个特征空间上的训练数据集

\[D = \left\{(x_1,y_1),(x_2,y_2),...,(x_N,x_N)\right\} \]

　　其中，$x_i∈\mathcal{X} = R^n,y_i∈\mathcal{Y}=\left\{+1,-1\right\},i=1,2,...,N$。$x_i$为第$i$个特征向量，也称为实例，$y_i$为$x_i$的类标记。当$y_i=+1$时，称$x_i$为正例；当$y_i＝－１$时，称$x_i$为负例。$(x_i,y_i)$称为样本点。这里假设训练数据集合是线性可分的。

　　则这时分类学习的目标，是在特征空间中找到一个分离超平面，能将实例分到不同的类。
　　划分超平面可以通过如下线性方程来描述：

\[W^Tx + b = 0 \quad \quad (6.1) \]

　　其中$w＝(w_1; w_2;...;w_d)$为法向量，决定了超平面的方向；
　　$b$为位移项，决定了超平面与原点之间的距离。显然，划分超平面可被法向量$w$和位移$b$确定。超平面可用$(w,b)$来表示。分离超平面将特征空间划分为两部分，一部分为法向量指向一侧的正类，一部分为法向量指向另一侧的负类。

　　对于二分类学习，给定训练样本集合$D = \left\{(x_1,y_1),(x_2,y_2),...,(x_m,y_m) \right\},y_i ∈\left\{-1,+1\right\}$。假设现在的数据是线性可分的，这时分类学习最基本的想法就是找到一个合适的超平面，该超平面能够将不同类别的样本分开。但能将训练样本分开的超平面有很多，我们的问题是从中找出鲁棒性最强，泛化能力最好的一个超平面。
例如下图所示，我们应该努力去找到哪一个呢？

　　直观上来看，应该去找位于两类训练样本“正中间”的划分超平面，也即图中黑色加粗的那一个，因为该划分超平面对训练样本局部扰动的“容忍性”最好。例如，由于训练集的局限性或噪声的因素，训练集外的样本可能比图中的训练样本更接近两个类的分割界限，这将使许多划分超平面出现错误，而黑色加粗的超平面受影响最小。换言之，这个划分超平面所产生的分类结果是最鲁棒的，对未见示例的泛化能力最强。

　　因此，对训练样本集合中的数据点进行划分时候，易知：当超平面距离与它最近的数据点的间隔越大，分类的鲁棒性越好，即当新的数据点加入时候，超平面对于这些点的适应性最强，出错的可能性最小。因此，需要让所选择的超平面能够最大化这个间隔（Gap）。　　

　　一般地，当训练数据集线性可分时，存在无穷个分离超平面可将两类数据正确分开，感知机利用误分类最小的策略，求得分离超平面，不管这时的解有无穷多个，线性可分支持向量机利用间隔最大化(硬间隔最大化)求最优分离超平面时，这时，解是唯一的。

1.2 间隔

　　一般来说，在样本空间中，一个点距离分离超平面的远近，可以表示分类预测的确信程度。在超平面$w\cdot x＋b=0$确定的情况下，$|w\cdot x+b|$能够相对地表示点$x$距离超平面的远近。而$w \cdot x+b$的符号与类标记$y$的符号能否一致表示分类是否正确。
　　样本空间(数据集)中任意点x到超平面$(w,b)$的距离可写为

\[r = \frac{|w^Tx+b|}{||w||} \quad \quad (6.2) \]

式(6.2)的推导：

在推导之前先讨论两点预备知识：
[向量投影]
两个向量的内积(点乘)：$a \cdot b = a^Tb = ||a|| ||b||cos(\theta)$.
$a$在$b$上的投影长度为$||a||cos(\theta) = \frac{a \cdot b}{||b||}$.
$b$在$a$上的投影长度为$||b||cos(\theta) = \frac{a \cdot b}{||a||}$.
注意：以上计算投影长度的公式仅适用于当$\theta < \frac{\pi}{2}$时，若$\frac{\pi}{2} < \theta < \pi$，则$cos(\theta) < 0$，计算投影的公式应取绝对值。

[超平面法向量]
超平面$w^Tx + b = 0$的法向量为$w$(当$w$为二维向量时则是一条直线)，例如：
当$w = (1,1), b= 0$时，超平面即为直线$x_1 + x_2 = 0$。
注意：$x_1 + x_2 = 0$可理解为我们常见的$y = -x$，但$x_1 + x_2 = 0$更侧重于描述直线本身，而$y = -x$则强调$y$随$x$的线性变化。
有关超平面法向量，可以用更通用的证明：
任意取超平面上两点$x',x''$(即满足超平面方程$w^Tx' + b = 0$,$w^Tx''+b = 0$)
则两点的连线$x' - x''$一定在这个超平面上
又因为$w^T(x' - x'') = w^Tx' + b - (w^Tx'' + b) = 0$
即$w \perp (x' - x'')$(向量内积等于零，说明两者垂直)
即$w$垂直于超平面上任意向量$x - x''$，也就是说$w$是超平面的法向量，得证。

下面正式开始推导式(6.2)$r = \frac{|w^Tx+b|}{||w||}$.
已知超平面$w^Tx + b = 0$，求空间中任意点$x$到该超平面的距离。
任意取超平面上一个点$x'$，则点$x$到超平面的距离等于向量$(x - x')$在法向量$w$的投影长度
$dist = \frac{|w^T(x - x')|}{||w||} = \frac{|w^Tx - w^Tx'|}{||w||} = \frac{|w^Tx + b|}{||w||}$.
注意：上式推导过程中，分子之所以要取绝对值是由于向量内积可能小于零；另外，由于$x'$是超平面上的点，因此$w^Tx' + b = 0$，即$b = -w^Tx'$.

我们定义间隔(Margin)$\gamma$为整个数据集D中所有样本到分割超平面的最短距离，也即两个异类支持向量到超平面的距离之和为

\[\gamma = \underset{n}{min}\gamma_n = \frac{2}{||w||} \quad \quad (6.4) \]

式(6.4)的推导

注意到，距离超平面最近的训练样本$(x_i,y_i)$利用使得(6.3)的等号成立，即为
$\left\{\begin{matrix} w^Tx_i + b = +1，\quad y_i = +1; \\ w^Tx_i + b = -1, \quad y_i = -1 \end{matrix}\right.$，则根据式(6.2)可知，这些点(即候选支持向量)到超平面的距离为
$dist = \frac{|w^Tx + b|}{||w||} = \frac{1}{||w||}$.
那么容易知道，两个异类支持向量到超平面的距离之和为$\frac{2}{||w||}$.　　

欲找到具有“最大间隔”（maximum margin）的划分超平面，也就是要找到能满足$\left\{\begin{matrix} w^Tx_i + b ≥ +1，\quad y_i = +1; \\ w^Tx_i + b ≤ -1, \quad y_i = -1 \end{matrix}\right. \quad \quad (6.3)$中约束的参数法向量$w$和位移$b$，使得间隔$\gamma$最大，即

\[\begin{align} &\underset{w,b}{max} \frac{2}{||w||} 　等价于　\underset{w,b}{min} \frac{1}{2}||w||^2 \\　&s.t　y_i(w^Tx_i+b)≥1,　i=1,2,...,m \quad \quad (6.6) \end{align} \]

　　显然，为了最大化间隔，仅需要最大化$||w||^{-1}$，这等价于最小化$||w||^2$。

式(6.6)的解释

式(6.6)的约束条件，意味着训练样本线性可分，也就是说不存在被分类错误的样本，因此也就不存在欠拟合问题；已知优化式(6.6)的目标函数是在寻找“最大间隔”的划分超平面，而“最大间隔”划分超平面所产生的分类结果是最鲁棒的，对未见示例的泛化能力最强，因此可将式(6.6)的优化目标进一步解释为“最小化$\frac{1}{2}||w||^2$则相当于寻找最不可能过拟合的分类超平面”。同时，为了防止过拟合，我们引入了正则化(Regularization)，而正则化就是在最小化的目标函数中加入分类器的所有参数的模值的平方(不含位移项)，与此正好不谋而合。

　　对于一个线性可分的数据集，其分割超平面有很多个，但是间隔最大的超平面是唯一的。
　　下图给定了支持向量机的最大间隔分割超平面的示例，其中轮廓线加粗的样本点为支持向量。

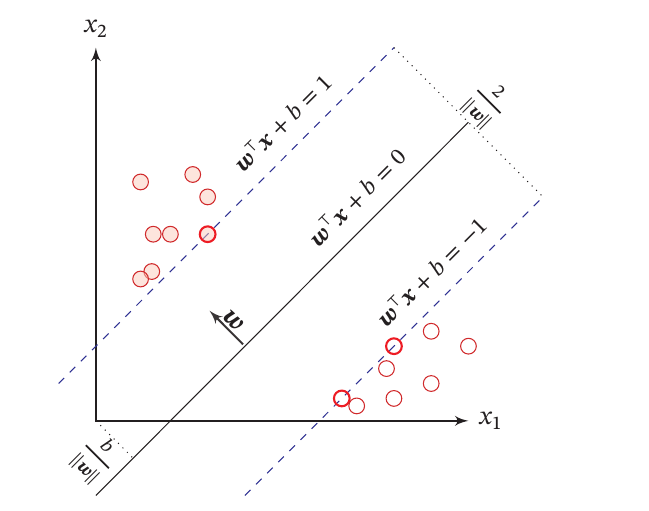
　　这就是支持向量机(Support Vector Machine，简称SVM)的基本型。

算法1 (线性可分支持向量机学习算法——最大间隔法)

输入：线性可分训练数据集Ｔ={$(x_1,y_1),(x_2,y_2),...,(x_N,y_N)$}，其中，$x_i∈\mathcal{X}=R^n,y_i∈\left\{-1.+1 \right\},i = 1,2,...,N$;
输出：最大间隔分离超平面和分类决策函数。
(1)选择惩罚参数$C>0$，构造并求解约束最优化问题(凸二次规划问题)：

\[\underset{w,b}{min} \frac{1}{2}||w||^2 \\ \text{s.t}　y_i(w\cdot x_i+b)-1≥0,\quad i=1,2,...,N \]

转换为凸二次规划问题，等价于

\[\begin{align} &\underset{\alpha}{min} \quad \frac{1}{2} \sum \limits_{i=1}^N \sum \limits_{j=1}^N \alpha_i \alpha_j y_i y_j (x_i \cdot x_j) - \sum \limits_{i=1}^N \alpha_i \\ &\text{s.t}. \quad \sum \limits_{i=1}^N \alpha_i y_i = 0 \\ &0 \leq \alpha_i \leq C， \quad i=1,2,...,N \end{align} \]

(2)计算$w^*$和$b^{*}$：

\[w^* = \sum \limits_{i=1}^N \alpha_i^*y_ix_i \]

选择$\alpha^*$的一个分量$\alpha_j^*$满y足条件$0<\alpha_j^*<C$，计算

\[b^{*} = y_j - \sum \limits_{i=1}^N \alpha_i^*y_i(x_i \cdot x_j) \]

(3)求分离超平面

\[w^{*}\cdot x + b^{*} = 0 \]

分离决策函数：

\[f(x) = sign(w^* \cdot x+b^*) \]

例题1 求最大间隔分离超平面

已知一个如下图所示的训练数据集，其正例点是$x_1=(3,3)^T$,$x_2=(4,3)^T$,负例点是$x_3=(1,1)^T$，试求最大间隔分离超平面。

解按最大间隔算法，根据训练数据集约束最优化问题：

\[\underset{w,b}{min} \frac{1}{2} (w_1^2+w_2^2) \\ \text{s.t}　3w_1+3w_2+b ≥ 1 \\ 　　　　4w_1+3w_2+b ≥１　\\ 　　　-w_1-w_2-b≥1 \]

求得此最优化问题的解$w_1=w_2=\frac{1}{2},b=-2$。
于是最大间隔分离超平面为

\[\frac{1}{2}x^{(1)}+\frac{1}{2}x^{2}-2 = 0 \]

其中，$x_1=(3,3)^T$与$x_3=(1,1)^T$为支持向量。

1.2 支持向量

　　假设超平面$(w,b)$能将训练样本正确分类，即对于$(x_i,y_i)∈D$，若$y_i = +1$,则有$w^Tx_i＋b>0$；若$y_i = -1$,则有$w^Tx_i+b$。令

\[\left\{\begin{matrix} w^Tx_i + b ≥ +1，\quad y_i = +1; \\ w^Tx_i + b ≤ -1, \quad y_i = -1 \end{matrix}\right. \]

　　在线性可分情况下，训练数据集的样本点中与分离超平面距离最近的样本点的实例称为“支持向量”(support vector)。同时，支持向量是使约束条件成立的点。

　　如下图所示，图像中黑色加粗的实线即为分离超平面，这里根据约束条件划分出上下两个超平面(以虚线表示)。为了讨论方便，这里我们令上方(顺法向量的一侧)正例超平面为$H1$,下方的负例超平面为$H2$.
　　于是，对$y_i=+1$的正例点，支持向量在超平面$H1:w\cdot x+b=1$上；
　　对$y_i＝-1$的负例点，支持向量在超平面$H2:w\cdot x+b=-1$上。
　　由此，在$H1$和$H2$上的点就是支持向量。

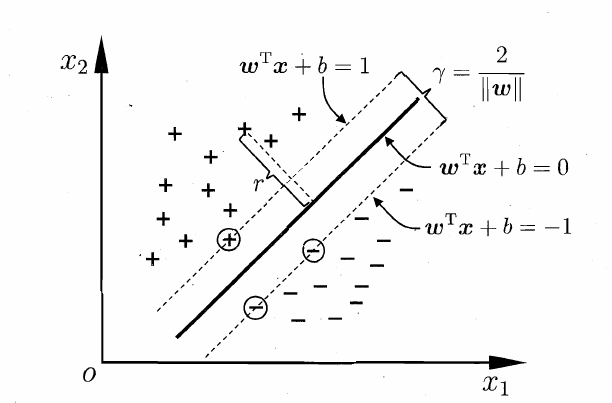
　　又注意到$H1$和$H2$两个平面平行，并且没有实例点落在它们中间。在$H1$和$H2$之间形成了一条长带，分离超平面与它们平行且位于它们中央。长带的宽度，即$H1$和$H2$的距离，称为间隔$\gamma$(margin)。
间隔依赖于分离超平面的法向量$w$，等价于$\frac{2}{||w||}$。相应的，我们又将$H1$和$H2$称为间隔边界。

　　在决定分离超平面时，只有支持向量起作用，而其他实例点并不起作用。如果移动支持向量，将会改变所求的解；但是如果在间隔边界意外移动其他实例点，甚至去掉这些点，则解是不会发生改变的。由于支持向量在确定分离超平面中起着确定性作用，因此将这种分离模型称为支持向量机。

　　支持向量的个数一般很少，所以支持向量机是由很少的“重要的”训练样本确定的。　

　　在考虑原始最优化问题及对偶最优化问题时，将训练数据集中对应于$\alpha_i^*>0$的样本点$(x_i,y_i)$的实例$x_i∈R^n$称为支持向量。

1.3 从原始优化问题到对偶问题

　　将下式作为原始最优化问题(也是一个凸二次规划问题(convex quadratic programming))，

\[\underset{w,b}{min} \frac{1}{2}||w||^2 \\ \text{s.t}. y_i(w \cdot x_i+b)-1 ≥ 0, \quad i=1,2,...N \]

要直接求解这个问题较为复杂，这里我们应用拉格朗日对偶型，通过求解对偶问题(dual problem)得到原始问题(primal problem)的最优解，这就是线性可分支持向量机的对偶算法(dual algorithm)。这样做的优点，一是对偶问题往往更容易求解；二是自然引入核函数，进而推广到非线性分类问题。
　　
　　
　　对于当前的优化问题，首先，通过拉格朗日乘子，构建拉格朗日函数。

\[L(w,b,\alpha) = \frac{1}{2}||w||^2 + \sum \limits_{i=1}^N \alpha_i(1-y_i(w \cdot x + b)) \quad \quad (6.8)\\ = \frac{1}{2}||w||^2 - \sum \limits_{i=1}^N \alpha_i y_i(w \cdot x_i+b)+\sum \limits_{i=1}^N \alpha_i \\ = \frac{1}{2}w^Tw + \sum \limits_{i=1}^m \alpha_i - \sum \limits_{i=1}^m \alpha_i y_i w^T x_i - \sum \limits_{i=1}^m \alpha_i y_ib \]

　　其中，$\alpha=(\alpha_1,\alpha_2,...,\alpha_N)^T$为拉格朗日乘子向量。
令$L(w,b,\alpha)$对$w$和$b$的偏导为零可得

\[\begin{align} &w = \sum \limits_{i=1}^m \alpha_i y_i x_i \quad \quad (6.9) \\ &0 = \sum \limits_{i=1}^m \alpha_i y_i \quad \quad (6.10) \end{align} \]

式(6.9)的推导

式(6.8)对$w$求偏导可得(与$w$无关的项求偏导后均等于零)：
$\frac{\partial L(w,b, \alpha)}{\partial w} = w - \sum \limits_{i=1}^m \alpha_i y_i x_i$.
令偏导等于零即可得式(6.9):
$w - \sum \limits_{i=1}^m \alpha_i y_i x_i = 0 \Rightarrow w = \sum \limits_{i=1}^m \alpha_i y_i x_i$.

式(6.10)的推导

式(6.8)对$b$求偏导可得(与$b$无关的项求偏导后均等于零):
$\frac{\partial L(w,b,\alpha)}{\partial b} = -\sum \limits_{i=1}^m \alpha_i y_i$.
令偏导等于零即可得式(6.10):
$-\sum \limits_{i=1}^m \alpha_i y_i = 0 \Rightarrow \sum \limits_{i=1}^m \alpha_i y_i = 0$.

　　根据拉格朗日对偶性，原始问题的对偶问题是极大极小问题

\[\underset{\alpha}{max} \underset{w,b}{min}L(w,b,\alpha) \]

所以，为了得到对偶问题的解，需要先求$L(w,b,\alpha)$对$w,b$的极小，再求对$\alpha$的极大。

(1)求$\underset{w,b}{min}L(w,b,\alpha)$.
将拉格朗日函数$L(w,b,\alpha)$分别对$w,b$求偏导数并令其等于0。

\[\begin{align} &\nabla_w L(w,b,\alpha) = \frac{\partial L(w,b,\alpha)}{\partial w}= w-\sum \limits_{i=1}^N \alpha_i y_i x_i = 0 \Rightarrow w = \sum \limits_{i=1}^N \alpha_i y_i x_i \\ &\nabla_b L(w,b,\alpha) = \frac{\partial L(w,b,\alpha)}{\partial b} = -\sum \limits_{i=1}^N \alpha_i y_i = 0 \Rightarrow \sum \limits_{i=1}^N \alpha_i y_i = 0 \end{align} \]

将$w = \sum \limits_{i=1}^N \alpha_i y_i x_i$代入拉格朗日函数$L(w,b,\alpha) = \frac{1}{2}||w||^2 - \sum \limits_{i=1}^N \alpha_i y_i(w \cdot x_i+b)+\sum \limits_{i=1}^N \alpha_i$，并利用$\sum \limits_{i=1}^N \alpha_i y_i = 0$，即得

\[L(w,b,\alpha) = \frac{1}{2} \sum \limits_{i=1}^N \sum \limits_{j=1}^N \alpha_i \alpha_j y_j y_i(x_i \cdot x_j) - \sum \limits_{i=1}^N \alpha_i y_i \left(\left(\sum \limits_{j=1}^N \alpha_j y_j x_j\right)\cdot x_i + b\right) + \sum \limits_{i=1}^N \alpha_i \\ = -\frac{1}{2} \sum \limits_{i=1}^N \sum \limits_{j=1}^N \alpha_i \alpha_jy_iy_j(x_i \cdot x_j)+\sum \limits_{i=1}^N \alpha_i \]

　　也即

\[\underset{w,b}{min} L(w,b,\alpha) = -\frac{1}{2} \sum \limits_{i=1}^N \sum \limits_{j=1}^N \alpha_i \alpha_j y_i y_j(x_i^T \cdot x_j) + \sum \limits_{i=1}^N \alpha_i \]

(2)求$\underset{w,b}{min}L(w,b,\alpha)$对$\alpha$的极大，即是对偶问题

\[\begin{align} &\underset{\alpha}{max} \quad \sum \limits_{i=1}^N \alpha_i -\frac{1}{2} \sum \limits_{i=1}^N \sum \limits_{j=1}^N \alpha_i \alpha_j y_i y_j(x_i^T \cdot x_j) \quad (6.11)\\ &\text{s.t}.　\sum \limits_{i=1}^N \alpha_i y_j = 0 \\ &\alpha_i≥0,\quad i = 1,2,...,N \end{align} \]

对式(6.11)的推导

式(6.11)即为式(6.6)的对偶问题，这里主要推导式(6.11)的目标函数，即将根据式(6.9)(6.10)将式(6.8)转化为式(6.11)目标函数的过程。将式(6.8)继续整理为
$L(w,b,\alpha) = \frac{1}{2}w^Tw + \sum \limits_{i=1}^N \alpha_i - \sum \limits_{i=1}^N \alpha_i y_i w^T x_i - \sum \limits_{i=1}^N \alpha_i y_i b \\=\frac{1}{2}w^Tw + \sum \limits_{i=1}^N\alpha_i - w^T \left(\sum \limits_{i=1}^N \alpha_i y_i x_i \right) - b \left(\sum \limits_{i=1}^N\alpha_i y_i \right)$.

其中后两项的变形是因为与求和变量无关的项(即相对于求和变量来说是一个常量)可以拿到求和号外面(即提公因式)，再结合式(6.9)(6.10):
$L(w,b, \alpha) = \frac{1}{2}w^Tw + \sum \limits_{i=1}^N \alpha_i - w^Tw - o \\ =\sum \limits_{i=1}^N \alpha_i - \frac{1}{2}w^Tw$.

将(6.9)代入即可得式(6.11)
$L(w,b,\alpha) = \sum \limits_{i=1}^N \alpha_i - \frac{1}{2}w^Tw \\ =\sum \limits_{i=1}^N \alpha_i - \frac{1}{2} \left(\sum \limits_{i=1}^N \alpha_i y_i x_i \right)^T \left(\sum \limits_{j=1}^N \alpha_j y_j x_j \right) \\ = \sum \limits_{i=1}^N \alpha_i -\frac{1}{2}\sum \limits_{i=1}^N \sum \limits_{j=1}^N \alpha_i\alpha_j y_i y_j x_i^T x_j$.

将上式的目标函数由求极大转换到求极小，就得到了下面与之等价的对偶最优化问题：

\[\begin{align} &\underset{\alpha}{min} \frac{1}{2} \sum \limits_{i=1}^N \sum \limits_{j=1}^N \alpha_i \alpha_j y_i y_j(x_i^T \cdot x_y) - \sum \limits_{i=1}^N \alpha_i \\ &\text{s.t}.　\sum \limits_{i=1}^N　\alpha_i y_i = 0 \\ &\alpha_i≥0, \quad i=1,2,...,N \end{align} \]

考虑原始最优化问题和对偶最优化问题，原始问题满足下面的Karush-Kuhn-Tucker(KKT)条件：

\[\left\{\begin{matrix} \alpha_i \geq 0; \\ y_if(x_i) - 1 \geq 0; \\ \alpha(y_if(x_i) - 1) = 0. \end{matrix}\right. \quad \quad (6.13) \]

解释说明：
第1个是要求不等式约束的拉格朗日乘子不小于0;
第2个就是式(6.6)的约束条件，只是用$f(x_i)$替代了$w^Tx_i+b$表达形式并进行了移项；
第3个表示前两个式子中必有其一等于0，当$\alpha_i=0$时表示其对应的不等式约束不起作用，也就是说极值点位于不等式约束区域内部，当$\alpha_i>0$时表示极值点位于不等式约束区域边缘，即$y_if(x_i)-1 = 0$。
为什么要求不等式约束的拉格朗日乘子不小于0呢？这里主要有两个方面的原因：

其一，是为了保证式(6.8)$L(ww,b,\lambda) = \frac{1}{2}||w||^22 + \sum \limits_{i=1}^m \alpha_i(1 - y_i(w^Tx_i + b))$的拉格朗日函数$L(w,b,\lambda)$不大于原始问题目标函数$\frac{1}{2}||w||^2$；

其二，当$\alpha_i > 0$时表示极值点位于不等式约束区域边缘，此时$\alpha_i>0$保证了原始问题目标函数的梯度方向与约束函数的梯度方向相反(可参见西瓜书附录B.1的式(B.1)，当$\lambda>0$时两个梯度正负号一定相反)，梯度方向是使得函数值增加最快的方向(梯度反方向则是使得函数值下降最快的方向)，当约束区域边缘某点取得极值时，在该点目标函数的梯度方向一定是朝向约束区域内部的(梯度反方向使函数值下降，此时梯度反方向指向约束区域外部，自变量不能在外部取值，因此函数值不能再下降了，即取得极小值)，而约束函数的梯度方向一定是朝向约束区域外部的(因为约束函数为小于等于零类型，约束区域外部即为约束函数大于零的自变量区域，梯度方向肯定指向能使约束函数的函数值增加的方向，即外部)。

\[\begin{align} &\nabla_xL(x^*,\alpha^*, \beta^*) = 0 \\ &\alpha_i^*c_i(x^*) = 0, \quad i = 1,2,...,k \\ &c_i(x^*) ≤ 0, \quad i = 1,2,...,k \\ &\alpha_i^* ≥ 0, \quad i = 1,2,...,k \\ &h_j(x)^* = 0,\quad j = 1,2,...,l \end{align} \]
其中，$\alpha_i^*c_i(x^*) = 0, \quad i = 1,2,...,k$称为KKT的对偶互补条件。
由此条件可知：若$\alpha_i^*>0$则$c_i(x^*)=0$.

　　所以存在$w^{*},\alpha^*,\beta^*$，使得$w^*$是原始问题的解，$\alpha^*,\beta^*$是对偶问题的解。这意味着求解原始问题可以转换为求解对偶问题。
　　
　　对线性可分训练数据集，假设对偶最优化问题对$\alpha$的解为$\alpha^*=(a_1^*,a_2^*,...,\alpha_N^*)$，可以由$\alpha^*$求得原始最优化问题对$(w,b)$的解$\alpha^{*},\beta^*$.

　　于是有下面的定理。
　　设$\alpha^* = (\alpha_1^*,\alpha_2^*,...,\alpha_l^*)$是对偶最优化问题的解，则存在下标$j$，使得$\alpha_j^*>0$，并可按下式求得原始最优化问题的解$w^*,b^*$:

\[\begin{align} &w^* = \sum \limits_{i=1}^N \alpha_i^* y_i x_i \\ &b^* = y_j - \sum \limits_{i=1}^N \alpha_i^* y_i(x_i \cdot x_j) \end{align} \]

由此定理可知，分类超平面可以写成($\sum \limits_{i=1}^N \alpha_i^*y_i(x\cdot x_i) $)

\[\sum \limits_{i=1}^N \alpha_i^* y_i(x \cdot x_i) + b^* = 0 \]

分类决策函数可以写成(下式称为线性可分支持向量机的对偶形式)

\[f(x) = sign \left(\sum \limits_{i=1}^N \alpha_i^*y_i(x \cdot x_i) + b^* \right) \]

这就是说，分类决策函数只依赖于输入$x$和训练样本输入的内积。

综上所述，对于给定的线性可分训练数据集，可以首先求得对偶问题的解$\alpha^*$；
再利用$w^* = \sum \limits_{i=1}^N \alpha_i^* y_i x_i$和$b^* = y_j - \sum \limits_{i=1}^N \alpha_i^* y_i(x_i \cdot x_j)$求得原始问题的解$w^*,b^*$;
从而得到分离超平面及分类决策函数。
这种算法称为线性可分支持向量机的对偶学习算法，是线性可分支持向量机学习的基本算法。

算法2 (线性可分支持向量机学习算法)

输入: 线性可分训练集Ｔ=${(x_1,y_1),(x_2,y_2),...,(x_N,y_N)}$，其中$x_i∈\mathcal{X}=R^n,y_i∈\mathcal{Y}＝\left\{-1,+1\right\},i=1,2,...,N$；
输出：分离超平面和分类决策函数
(1)构造并求解约束最优化问题

求得最优解$\alpha^{*}=(\alpha_1^*,\alpha_2^*,...,\alpha_N^*)^T$。
(2)计算$w^* = \sum \limits_{i=1}^N \alpha_i^*y_ix_i$.
并选择$\alpha^*$的一个正分量$\alpha_j^*>0$，计算

\[b^* = y_j - \sum \limits_{i=1}^N \alpha_i^*y_j(x_i \cdot x_j) \]

(3)求得分离超平面

\[w^* \cdot x + b^* = 0 \]

分类决策函数：

\[f(x)=sign(w^*\cdot x+b^*) \]

在线性可分支持向量机中，由$w^* = \sum \limits_{i=1}^N\alpha_i^*y_ix_i$和$b^* = y_j - \sum \limits_{i=1}^N\alpha_i^*y_i(x_i\cdot x_j)$可知，$w^*$和$b^*$只依赖于训练数据中对应于$\alpha_i^*>0$的样本点$(x_i,y_i)$，而其他样本点对$w^*$和$b^*$没有影响。我们将训练数据中对应于$\alpha_i^*>０$的实例点$x_i∈R^n$称为支持向量。

例题2 求线性可分支持向量积

如下图所示，正例点是$x_1=(3,3)^T,x_2 = (4,3)^T$，负例点是$x_3 = (1,1)^T$，试用上述算法求线性可分向量机。

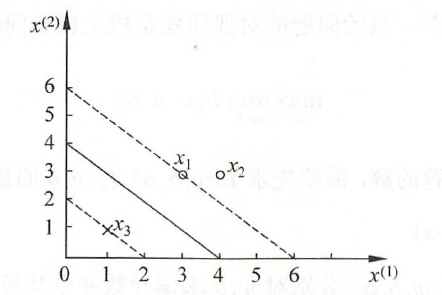
解: 根据所给数据，对偶问题是

\[\begin{align} &\underset{\alpha}{min} \frac{1}{2} \sum \limits_{i=1}^N \sum \limits_{j=1}^N \alpha_i \alpha_j y_i y_j(x_i \cdot x_j) - \sum \limits_{i=1}^N \alpha_i \\ &= \frac{1}{2} (18\alpha_1^2 + 25 \alpha_2^2 + 2\alpha_3^2 + 42\alpha_1 \alpha_2 -12\alpha_1\alpha_3 - 14\alpha_2\alpha_3 -14\alpha_2\alpha_3) - \alpha_1 -\alpha_2 - \alpha_3 \\ &\text{s.t}　\alpha_1 + \alpha_2 - \alpha_3 = 0 \\ &\alpha_i \ge 0, \quad i = 1,2,3 \end{align} \]

　　解这最优化问题。将$\alpha_3＝\alpha_1+\alpha_2$代入目标函数并记为

\[s(\alpha_1,\alpha_2) = 4\alpha_1^2 + \frac{13}{2} \alpha_2^2 + 10\alpha_1\alpha_2 -2\alpha_1 - 2\alpha_2 \]

对$\alpha_1,\alpha_2$求偏导数并令其为0，易知$s(\alpha_1,\alpha_2)$在点$(\frac{3}{2},-1)^T$取极值，但该点不满足约束条件$\alpha_2 \ge 0$，所以最小值应在边界上得到。
　　
　　当$\alpha_1=0$，最小值$s(0,\frac{2}{13})=-\frac{2}{13}$；当$\alpha_2=0$时，最小值$s(\frac{1}{4},0) = -\frac{1}{4}$。于是$s(\alpha_1,\alpha_2)$在$\alpha=\frac{1}{4},\alpha_2=0$达到最小，此时$\alpha_3 = \alpha_1 + \alpha_2 = \frac{1}{4}$。

　　这样，$\alpha_1^* = \alpha_3^* = \frac{1}{4}$对应的实例点$x_1,x_3$是支持向量。
　　根据$w^* = \sum \limits_{i=1}^N \alpha_i^* y_i x_i$和$b^* = y_j - \sum \limits_{i=1}^N \alpha_i^* y_i(x_i \cdot x_j)$计算得

\[w_1^* = w_2^* = \frac{1}{2} \\ b^* = -2 \]

分离超平面为

\[\frac{1}{2}x^{(1)} + \frac{1}{2} x^{(2)} - 2 = 0 \]

分类决策函数为

\[f(x) =sign(\frac{1}{2}x^{(1)} + \frac{1}{2}x^{(2)} - 2) \]

对于线性可分问题，上述线性可分支持向量机的学习(硬间隔最大化)算法是完美的。但是，训练数据集线性可分是理想的情形。在现实问题中，训练数据集往往是线性不可分的，即在样本中出现噪声或特异点。

算法3 非线性支持向量机学习算法

输入：线性不可分训练集Ｔ=${(x_1,y_1),(x_2,y_2),...,(x_N,y_N)}$，其中$x_i∈\mathcal{X}=\mathbb{R}^n,y_i∈\mathcal{Y}＝\left\{-1,+1\right\},i=1,2,...,N$；
输出：分离超平面和分类决策函数
(1) 选取适当的核函数$\kappa(x_i,x_j)$和惩罚参数$C>0$，构造并求解凸二次规划问题

\[\begin{align} &\underset{\alpha}{min} \frac{1}{2} \sum \limits_{i=1}^N \sum \limits_{j=1}^N \alpha_i\alpha_j y_i y_j \kappa(x_i,x_j) - \sum \limits_{i=1}^N \alpha_i \\ &\text{s.t}. \quad \sum \limits_{i=1}^N \alpha_i y_i = 0 \\ &0 \leq \alpha_i \leq C,i = 1,2,...,N \end{align} \]

得到最优解$\alpha^* = (\alpha_1^{*}, \alpha_2^{*},...,\alpha_N^{*})$

(2) 计算相关参数
选择$\alpha^*$的一个分量$\alpha_j^*$满足条件$0<\alpha_i^*<C$，计算

\[b^* = y_j - \sum \limits_{i=1}^N \alpha_i^*y_i \kappa(x_i,x_j) \]

(3) 求解可得分类决策函数

\[f(x) = sign \left(\sum \limits_{i=1}^N \alpha_i^* y_i \kappa(x,x_i) + b^*\right) \]

这里试举例帮助理解，若引入高斯核函数

\[\kappa(x_i,x_j) = exp(-\frac{||x_i-x_j||^2}{2\sigma^2}), \quad \sigma>0 为高斯核的带宽 \]

则对应的SVM是高斯径向基函数分类器，在此情况下，分类决策函数为

\[f(x) = sign \left(\sum \limits_{i=1}^N \alpha_i^* y_i exp(-\frac{||x_i-x_j||^2}{2\sigma^2}) + b^*\right) \]

算法4 SMO算法

SMO算法要解如下凸二次规划的对偶问题：

\[\begin{align} &\underset{\alpha}{min} \frac{1}{2} \sum \limits_{i=1}^N \sum \limits_{j=1}^N \alpha_i \alpha_j y_i y_j \kappa(x_i,x_j) - \sum \limits_{i=1}^N\alpha_i \\ &\text{s.t}. \quad \sum \limits_{i=1}^N \alpha_i y_i = 0 \\ &0 \leq \alpha_i \leq C, i=1,2，...,N \end{align} \]

在这个问题中，变量是拉格朗日乘子，一个变量$\alpha_i$对应于样本点$(x_i,y_i)$；变量的总数等于训练样本容量Ｎ。

　　SMO算法是一种启发式算法，其基本思路是：如果所有变量的解都满足此最优化问题的KKT条件，那么这个最优化问题的解就得到。因为KKT条件是该最优化问题的充分必要条件，否则选择两个变量，固定其他变量，针对这两个变量构建一个二次规划问题。这个二次规划问题关于这两个变量的解应该更接近原始二次规划问题的解，因为这会使得原始二次规划问题的目标函数变得更小。重要的是，这时子问题可以通过解析方法求解，这样就可以大大提高整个算法的计算速度。子问题有两个变量，一个是违反KKT条件最严重的那一个，另一个由约束条件自动确定。如此，SMO算法将原问题不断分解为子问题并对子问题求解，进而达到求解原问题的目的。
　　
注意，子问题的两个变量中只有一个是自由变量。假设$\alpha_1,\alpha_2$为两个变量，$\alpha_3,\alpha_3,...,\alpha_N$固定，那么由等式约束条件可知

\[\alpha_1 = -y_1 \sum \limits_{i=2}^N \alpha_i y_i \]

如果$\alpha_2$确定，那么$\alpha_1$也随之确定。所以子问题中同时更新两个变量。

整个SMO算法包括两个部分：求解两个变量二次规划的解析方法和选择变量的启发式方法。
输入：训练数据集Ｔ={$(x_1,y_1),(x_2,y_2),...,(x_N,y_N)$}，其中，$x_i∈\mathcal{X}＝R^n$,$y_i∈\mathcal{Y}＝\left\{-1,+1\right\},i=1,2,...,N$，精度$\varepsilon$.
输出：近似解$\hat \alpha$。
(1) 取近似解$\alpha^{(0)}=0$，令k=0;
(2) 选取优化变量$\alpha_1^{(k)},\alpha_2^{(k)}$,解析求解两个变量的最优化问题

\[\begin{align} &\underset{\alpha_1,\alpha_2}{min} \quad W(\alpha_1,\alpha_2) = \frac{1}{2} \kappa_{11}\alpha_1^2 + \frac{1}{2} \kappa_{22}\alpha_2^2 + y_1y_2\kappa_{12}\alpha_1 \alpha_2 - \\ &(\alpha_1+\alpha_2) + y_1 \alpha_1 \sum \limits_{i=3}^N y_i \alpha_i \kappa_{i1} + y_2 \alpha_i \sum \limits_{i=3}^N y_i \alpha_i \kappa_{i2} \\ &\text{s.t}. \quad \alpha_1 y_1 + \alpha_2 y_2 = -\sum \limits_{i=3}^N y_i \alpha_i \\ &0 \leq \alpha_i \leq C, \quad i = 1,2 \\ &其中，\kappa_{ij} = \kappa(x_i,x_j), i,j = 1,2,...,N \end{align} \]

，求得最优解$\alpha_1^{(k+1)},\alpha_2^{(k+2)}$，更新$\alpha$为$\alpha^{(k+1)}$;
(3) 若在精度$\varepsilon$范围内满足停止条件

\[\sum \limits_{i=1}^N \alpha_i y_i = 0, \quad 0 \leq \alpha_i \leq C, i = 1,2,...,N　\\ y_i \cdot g(x_i) = \left\{\begin{matrix} \geq 1, \left\{x_i|\alpha_i = 0 \right\} \\ = 1, \left\{x_i|0 < \alpha_i < C \right\} \\ \leq 1, \left\{x_i|\alpha_i = C \right\} \\ \end{matrix}\right. \]

其中，

\[g(x_i) = \sum \limits_{j=1}^N \alpha_j y_j \kappa(x_i,x_j) + b \\ \]

则转(4)；否则令k=k+1,转(2)
(4)取$\hat \alpha = \alpha^{(k+1)}$。

为了避开训练过程中样本规模数量造成开销问题对训练本身的障碍，人们通过利用问题本身的特性，提出了很多高效算法，SMO(Sequential Minimal Optimization)是其中一个著名的代表。

SMO算法的基本思路是，先固定$\alpha_i$之外的所有参数，然后求$\alpha_i$上的极值。由于存在约束$\sum_{i=1}^m \alpha_i y_i = 0$，若固定$\alpha_i$之外的其他变量，则$\alpha_i$可由其他变量导出。于是，SMO每次选择两个变量$\alpha_i$和$\alpha_j$，并固定其他参数。这样，在参数初始化后，SMO不断执行如下两个步骤直至收敛：

选取一对需更新的变量，$\alpha_i$和$\alpha_j$；
固定$\alpha_i$和$\alpha_j$以外的参数，求解式(6.11)

\[\begin{align} &\underset{\alpha}{min} \sum \limits_{i=1}^m \sum \limits_{j=1}^m \alpha_i \alpha_j y_i y_j x_i^T x_j \\ &\text{s.t}. \quad \sum \limits_{i=1}^m \alpha_i y_j = 0 \\ &\alpha_i \ge 0, \quad i = 1,2,...,m. \]
\[ 获得更新后的$\alpha_i$和$\alpha_j$。注意到只需选取的$\alpha_i$和$\alpha_j$中有一个不满足KKT条件，目标函数就会在迭代后减小。直观来看,KKT条件违背的程度越大，则变量更新后可能导致的目标函数值减幅越大。　　于是，SMO先选取违背KKT条件程度最大的变量。第二个变量应选择一个使得目标函数值减小最快的变量，但由于比较各变量所对应的目标函数值减幅的复杂度过高，因此SMO采用了一个启发式：使选取的两变量所对应样本之间的间隔最大。一种直观的解释是，这样的两个变量有很大的差别，与对两个相似的变量进行更新相比，对它们进行更新会带给目标函数值更大的变化。 \]

具体来说，仅考虑$\alpha_i$和$\alpha_j$时，约束条件$\alpha_i \ge 0, i = 1,2,...,m.$可重写为

\[\alpha_i y_i + \alpha_j y_j = c, \quad \alpha_i \ge 0, \alpha_j \ge 0 \quad \quad (6.14) \]

其中

\[c = -\sum \limits_{k\neq i,j} \alpha_k y_k \quad \quad (6.15) \]

是使得$\sum \limits_{i=1}^m \alpha_i y_i = 0$成立的常数。
用

\[\alpha_i y_i + \alpha_j y_j = c \quad \quad (6.16) \]

消去变量$\alpha_j$，则得到一个关于$\alpha_i$的单变量二次规划问题，仅有的约束是$\alpha_i \geq 0$。
不难发现，这样的二次规划问题具有闭式解，于是不必调用数值优化算法即可高效地计算出更新后的$\alpha_i$和$\alpha_j$。

　　如何确定偏移项$b$呢？注意到对任意支持向量$(x_s,y_s)$都有$y_sf(x_s)=1$，即

\[y_s\left(\sum \limits_{i∈S} \alpha_i y_i x_i^T x_s + b\right) = 1　\quad \quad (6.17) \]

　　其中$S＝\left\{i|\alpha_i>0,i=1,2,...,m \right\}$为所有支持向量机的下标集。
　　
　　理论上，可选取任意支持向量并通过求解$y_s\left(\sum \limits_{i∈S} \alpha_i y_i x_i^T x_s + b\right) = 1$获得$b$，但现实任务中常采用一种更鲁棒的做法：使用所有支持向量求解的平均

\[b = \frac{1}{||S||} \sum \limits_{i∈S}\left(y_s -\sum \limits_{i∈S} \alpha_i y_i x_i^T x_s \right) \quad \quad (6.18) \]

1.4 核函数

由于上述的超平面只能解决线性可分的问题，对于线性不可分的问题，例如：异或问题，我们需要使用核函数将其进行推广。一般地，解决线性不可分问题时，常常采用映射的方式，将低维原始空间映射到高维特征空间，使得数据集在高维空间中变得线性可分，从而再使用线性学习器分类。之所以能这样处理的原因是，如果原始空间为有限维，即属性数有限，那么总是存在一个高维特征空间使得样本线性可分。

例如，在下图中，若将原始的二维空间映射到一个合适的三维空间，就能找到一个合适的划分超平面。

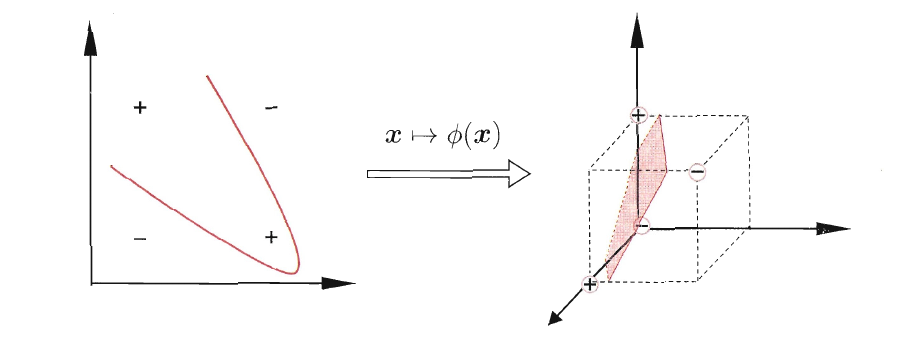
若令$\phi(x)$表示$x$映射后的特征向量，于是，在特征空间中的划分函数变为：

\[\begin{align} &f(x)=w^T \phi(x) + b　\quad (6.19) \\ &其中w和b是模型参数 \end{align} \]

需要注意的是，此时的$w$的维度与$\phi(x)$的维度相同，而不在与$x$维度相同。

按照同样的方法，有以下

\[\begin{array}{ll} {\displaystyle \min_{w,b}} \frac{1}{2}||w||^2 \quad \quad \quad \quad \qquad \quad \quad \quad \quad \quad (6.20)\\ {\text { s.t. }} {y_i(w^T\phi(x_i)+b)} ≥ 1, \quad i=1,2,...,m \end{array} \]

其对偶问题是

\[\begin{align} &\underset{\alpha}{max} \sum \limits_{i=1}^m \alpha_i - \frac{1}{2} \sum \limits_{i=1}^m \sum \limits_{j=1}^m \alpha_i \alpha_j y_i y_j \phi(x_i)^T\phi(x_j) \quad \quad (6.21)\\ &\text{s.t} \quad \sum \limits_{i=1}^m \alpha_i y_i = 0 \\ &\alpha_i \geq 0, \quad i=1,2,....,m. \end{align} \]

其中$\phi(x_i)^T\phi(x_j)$为样本$x_i$与$x_j$映射到特征空间之后的内积。

由于特征空间维数可能很高，甚至可能是无穷维，因此直接计算$\phi(x_i)^T\phi(x_j)$通常是困难的。

例如：若原始空间为二维，映射后的特征空间为5维，若原始空间为三维，映射后的特征空间将是19维，之后甚至可能出现无穷维，根本无法进行内积运算了。因此，核函数可以直接计算隐式映射到高维特征空间后的向量内积，而不需要显式地写出映射后的结果，它虽然完成了将特征从低维到高维的转换，但最终却是在低维空间中完成向量内积计算，与高维特征空间中的计算等效（低维计算，高维表现），从而避免了直接在高维空间无法计算的问题。

为了避开这个障碍，可以设想这样一个函数：　

\[\kappa(x_i,x_j) = \left\langle\phi\left(x_i\right), \phi\left(x_j \right)\right\rangle = \phi(x_i)^T\phi(x_j) \quad \quad (6.22) \]

即$x_i$与$x_j$在特征空间的内积等于它们在原始样本空间中通过函数$\kappa(\cdot,\cdot)$计算的结果。

式(6.22)的解释
此即核函数的定义，即核函数可以分解成两个向量的内积。要想了解某个核函数是如何将原始特征空间映射到更高维的特征空间的，只需要将$\kappa(x_i,x_j)$分解为两个表达形式完全一样的向量$\phi(x_i)$和$\phi(x_j)$即可(有时很难分解)。

通过上述函数，我们就不必直接去计算高维甚至无穷维度特征空间中的内积。

于是对偶问题改写为

\[\begin{align} &\underset{\alpha}{max} \sum \limits_{i=1}^m \alpha_i - \frac{1}{2} \sum \limits_{i=1}^m \sum \limits_{j=1}^m \alpha_i \alpha_j y_i y_j \kappa(x_i,x_j) \quad \quad (6.23)\\ &\text{s.t} \sum \limits_{i=1}^m \alpha_i y_i = 0 \\ &\alpha_i \geq 0, \quad i = 1,2,...,m. \end{align} \]

求解后即可得到

\[\begin{align} &f(x) = w^T \phi(x) + b \\ &= \sum \limits_{i=1}^m \alpha_i y_i \phi(x_i)^T \phi(x) + b \\ &= \sum \limits_{i=1}^m \alpha_i y_i \kappa(x,x_i) + b \quad \quad (6.24) \end{align} \]

其中，这里的函数$\kappa(\cdot,\cdot)$就是“核函数”(kernel function)。

上式显示出模型最优解可通过训练样本的核函数展开，这一展式亦称“支持向量展式”(support vector expansion)。

式(6.24)的解释
由式(6.24)的最终结果可以看出，对于未见示例$x$，支持向量机可以看作将原始特征$x$先进行特征变换$\hat x = [\kappa(x, x_1), \kappa(x,x_2),...,\kappa(x,x_m)]^T \in \mathbb{R}^m$，然后进行线性分类的结果，分类超平面为$f(\tilde{x}) = \tilde{w}^T\tilde{x}+b$，其中$\tilde{w} = [\alpha_1y_1, \alpha_2y_2,...,\alpha_m y_m]^T$。通过6.2节的推导可知，对于非支持向量，其$\alpha_i = 0$，因此特征转换实际并不需要$m$维，而是等于支持向量的个数。
下图摘自《Advances in Large Margin Classifiers》<Figure 1.4>: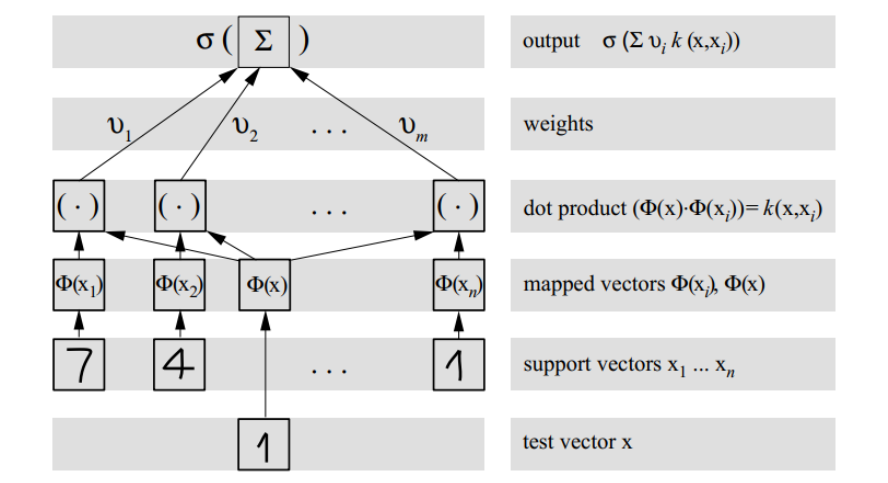

值得注意的是，上图的mapper vectors和dot product两层实际由核函数同时完成，这种结构与西瓜书108页5.5.1节介绍的RBF网络形式基本一致，不同的是这里进行特征转换时使用的是支持向量，而RBF网络则须以某种方式确定神经元中新；另外优化目标也有差异。

　　显然，若已知合适映射$\phi(\cdot)$的具体形式，则可写出核函数$\kappa(\cdot,\cdot)$。但在现实任务中我们通常不知道$\phi(\cdot)$是什么形式，那么合适的核函数是否一定存在呢

此时便引出了核函数（Kernel）的概念。

定义3（核：Kernel） 核是一个函数$K$，对所有$x,z \in \mathcal{X}$，满足$K(x,z)=\langle \phi(x), \phi(z) \rangle$，这里$\phi$是从$\mathcal{X}$到内积特征空间$\mathcal{F}$的映射

　　　在线性不可分问题中，核函数的选择成了支持向量机的最大变数，若选择了不合适的核函数，则意味着将样本映射到了一个不合适的特征空间，则极可能导致性能不佳。同时，核函数需要满足以下这个必要条件：

1.4.1 Mercer定理

定理6.1（核函数） 令$\mathcal{X}$为输入空间，$\kappa(\cdot, \cdot)$是定义在$\mathcal{X} \times \mathcal{X}$上的对称函数，则$\kappa$是核函数当且仅当对于任意数据$D=\{x_1,x_2,\ldots,x_m\}$，“核矩阵”（kernel matrix）$\mathbf{K}$总是半正定的：

\[\mathbf{K}=\left[\begin{array}{ccccc}{\kappa\left(x_1, x_1\right)} & {\cdots} & {\kappa\left(x_1, x_j\right)} & {\cdots} & {\kappa\left(x_1, x_m\right)} \\ {\vdots} & {\ddots} & {\vdots} & {\ddots} & {\vdots} \\ {\kappa\left(x_i, x_1\right)} & {\cdots} & {\kappa\left(x_i, x_j\right)} & {\cdots} & {\kappa\left(x_i, x_m\right)} \\ {\vdots} & {\ddots} & {\vdots} & {\ddots} & {\vdots} \\ {\kappa\left(x_m, x_1\right)} & {\cdots} & {\kappa\left(x_m, x_j\right)} & {\cdots} & {\kappa\left(x_m, x_m\right)}\end{array}\right] \]

1.4.2 常见的核函数

由于核函数的构造十分困难，通常我们都是从一些常用的核函数中选择，下面列出了几种常用的核函数：

名称	表达式	参数
线性核	$\kappa(x_i, x_j) = x_i^Tx_j$
多项式核	$\kappa(x_i,x_j) = (x_i^Tx_j)^d$	$d \ge 1$为多项式的次数
高斯核	$\kappa(x_i,y_j) = exp(-\frac{
拉普拉斯核	$\kappa(x_i,y_j) = exp(-\frac{
Sigmoid核	$\kappa(x_i,x_j) = tanh(\beta x_i^Tx_j + \theta)$	tanh为双曲正切函数，$\beta>０, \theta< 0$

当多项式核的阶为1时，其被称为线性核，对应的非线性分类器退化为线性分类器。高斯核（Gaussian kernel）也被称为RBF核，其对应的映射函数将样本空间映射至无限维空间。核函数的线性组合和笛卡尔积也是核函数，对特征空间内的函数也是核函数。此外，还可通过函数组合来得到核函数，例如

若$\kappa_1$和$\kappa_2$为核函数，对于任意正数$\gamma_1, \gamma_2$，其线性组合$\gamma_1 \kappa_1 + \gamma_2 \kappa_2$也为核函数。
若$\kappa_1$和$\kappa_2$为核函数，则核函数的直积$\kappa_1 \otimes \kappa_2(x,z) = \kappa_1(x,z)\kappa_2(x,z)$也为核函数。
若$\kappa_1$为核函数，则对于任意函数$g(x)$，$\kappa(x,z) = g(x)\kappa_1(x,z)g(z)$也为核函数

(二)软间隔与正则化

2.1 软间隔与硬间隔

　　前面的讨论中，我们主要解决了两个问题：
　　当数据线性可分时，直接使用最大间隔的超平面划分；
　　当数据线性不可分时，则通过核函数将数据映射到高维特征空间，使之线性可分。
　　实际上两者都是理想情况，我们一直假定训练样本在样本空间或特征空间是线性可分或可近似为线性可分，也即存在一个超平面能将不同类的样本完全划分开。

　　然而在现实问题和任务中，我们往往很难确定合适的核函数使得训练样本在特征空间中线性可分；退一步说，即便恰好找到了某个核函数使训练集在特征空间中线性可分，也很难断定这个貌似线性可分的结果不是由于过拟合所造成的。另外，对于某些情形还是很难处理，例如数据中有噪声的情形，噪声数据（outlier）本身就偏离了正常位置，但是在前面的SVM模型中，我们要求所有的样本数据都必须满足约束，如果不要这些噪声数据还好，当加入这些outlier后导致划分超平面被挤歪了，如下图所示，对支持向量机的泛化性能造成很大的影响。

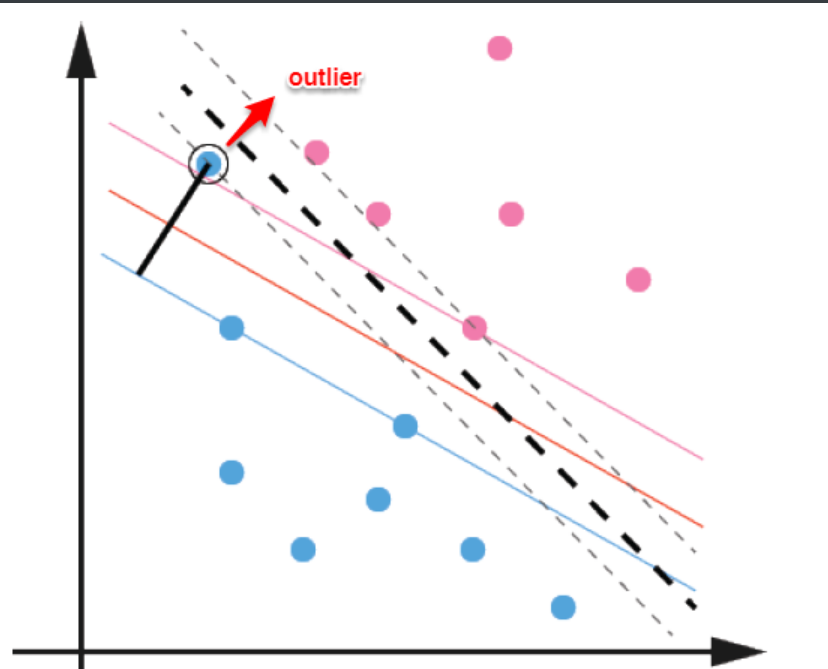
　　缓解该问题的一个办法是，允许支持向量机在一些样本上出错。为此，要引入“软间隔”(soft margin)的概念。如下图所示。(红色圈出了一些不满足约束的样本)

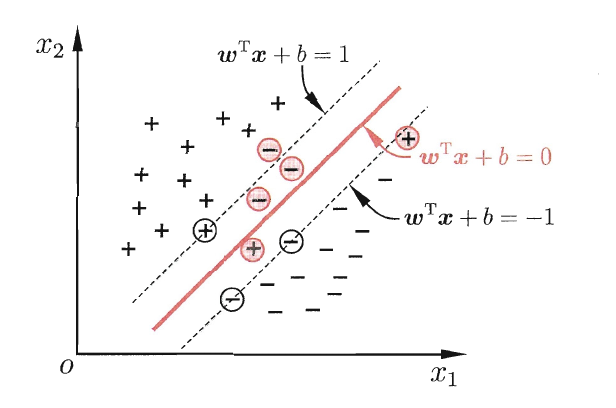
　　具体来说，支持向量机形式是要求所有样本均满足约束条件$\left\{\begin{matrix} w^Tx_i + b ≥ +1，\quad y_i = +1; \\ w^Tx_i + b ≤ -1, \quad y_i = -1 \end{matrix}\right.$，即所有样本都必须划分正确，这称为“硬间隔”(hard margin)，而软间隔则是允许某些样本不满足约束

\[y_i(w^Tx_i+b)≥1 \]

当然，在最大化间隔的同时，不满足约束的样本应尽可能少，于是，优化目标可以写为

\[\underset{w,b}{min} \frac{1}{2}||w||^2 + C\sum \limits_{i=1}^m\ell_{0/1}(y_i(w^Tx_i+b)-1) \]

　　其中当$C>0$是一个常数,$\ell_{0/1}$是“0/1损失函数”。
　　显然，当C为无穷大时，$\underset{w,b}{min} \frac{1}{2}||w||^2 + C\sum \limits_{i=1}^m\ell_{0/1}(y_i(w^Tx_i+b)-1)$迫使所有样本均满足$y_i(w^Tx_i+b)≥1$

　　然而，$\ell_{0/1}$非凸、非连续，数学性质不太好，使得$\underset{w,b}{min} \frac{1}{2}||w||^2 + C\sum \limits_{i=1}^m\ell_{0/1}(y_i(w^Tx_i+b)-1)$不易求解。于是，人民通常用其他一些函数$\ell_{0/1}$，称为“替代损失”(surrogate loss)。
替代损失函数一般具有较好的数学性质，如它们通常是凸的连续函数且是$\ell_{0/1}$的上界。

这里给出了三种常用的替代损失函数：　

hinge损失: $\ell_{hinge}(z) = max(0,1-z)$;
指数损失(exponential loss): $\ell_{exp}(z) = exp(-z)$;
对率损失(logistic loss): $\ell_{log} = log(1+exp(-z))$。

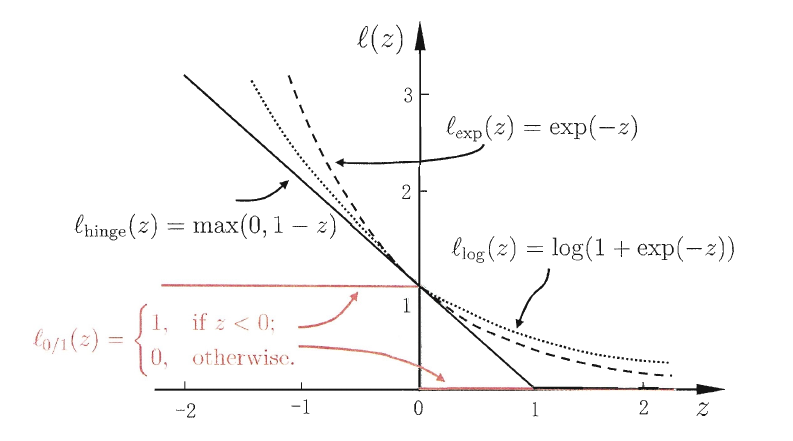
若采用$hinge$损失，则式子$\underset{w,b}{min} \frac{1}{2}||w||^2 + C\sum \limits_{i=1}^m\ell_{0/1}(y_i(w^Tx_i+b)-1)$变成

\[\underset{w,b}{min} \frac{1}{2}||w||^2 + C\sum \limits_{i=1}^m max(0,1-y_i(w^Tx_i+b)) \]

引入“松弛变量”(slack variables)$\xi≥0$，可将上式重写为

\[\underset{w,b,\xi_i}{min} \frac{1}{2}||w||^2 + C\sum \limits_{i=1}^m \xi_i \quad \quad (6.35) \]

\[\text{s.t}　y_i(w^Tx_i+b) ≥ 1 - \xi_i \\ \xi_i　≥ 0，\quad i=1,2,...,m. \]

这就是常用的“软间隔支持向量机”。

式(6.35)的推导

式(6.35)的推导
　　我们可以证明式(6.35)是式(6.34)的上限，最小化式(6.35)的同时也会最小化式(6.34)，这是因为：
由式(6.35)的约束条件$y_i(w^Tx_i+b)\geq 1 -\xi_i$可得$\xi_i \geq 1-y_i(w^Tx_i + b)$，再加上约束条件$\xi_i \geq 0$，即$\xi_i \geq 0$，即$\xi_i \geq 0$，即$\xi_i \geq max(0, 1 - y_i(w^Tx_i + b))$，因此式(6.35)是式(6.34)的上限。
　　式(6.34)的上限有很多种，那么就存在几个疑问，比如将式(6.34)中的第二部分换为式(6.32)或式(6.33)？
为什么式(6.35)对应的hinge损失呢？即为什么式(6.35)与式(6.34)等价？
　　式(6.35)的目标函数是最小化，即要求$\xi_i$越小越好：当$y_i(w^Tx_i+b)\geq1$成立时，$\xi_i = 0$(此时已经是$\xi_i$的最小值)即可保证$y_i(w^Tx_i + b) \geq 1- \xi_i$成立；而当$y_i(w^Tx_i + b) \geq 1$不成立时，$\xi_i = 1- y_i(w^Tx_i + b)$即可保证$y_i(w^Tx_i + b) \geq 1 - \xi_i$成立；当然，对于这两种情况也有其他$\xi_i$值可以使$y_i(w^Tx_i + b) \geq 1- \xi_i$成立，例如第一种情况中选$\xi_i > 0$的任意值也可以使不等式成立，第二种情况中选$\xi_i > 1 - y_i(w^Tx_i + b)$的任意值也可以使不等式成立，注意到之前的讨论所说“式(6.35)的目标函数是最小化，即要求$\xi_i$越小越好”，所以$\xi_i$的取值为$\xi_i = \left\{\begin{matrix} 1 - y_i(w^Tx_i + b), \quad y_i(w^Tx_i + b) < 1 \\ 0, \quad y_i(w^Tx_i + b) \geq 1 \end{matrix}\right.= max(0, 1 - y_i(w^Tx_i + b))$.从而得证。

　　显然，$\underset{w,b,\xi_i}{min} \frac{1}{2}||w||^2 + C\sum \limits_{i=1}^m \xi_i$中每个样本都有一个对应的松弛变量，用以表征该样本不满足约束$y_i(w^Tx_i+b)≥1$的程度。但是，这仍然是一个二次规划问题。于是，通过拉格朗乘子法可得到$\underset{w,b,\xi_i}{min} \frac{1}{2}||w||^2 + C\sum \limits_{i=1}^m \xi_i$的拉格朗日函数：

\[L(w,b,\alpha,\xi,\mu) = \frac{1}{2}||w||^2 + C\sum \limits_{i=1}^m \xi_i + \sum \limits_{i=1}^m \alpha_i(1-\xi_i -y_i(w^Tx_i+b)) - \sum \limits_{i=1}^m \mu_i\xi_i \quad \quad (6.36) \]

　　其中$\alpha_i≥0,\mu_i≥0$是拉格朗日乘子。
　　令$L(w,b,\alpha,\xi,\mu)$对$w,b,\xi_i$的偏导为零可得

\[\begin{aligned} \frac{\partial L}{\partial w} &=0 \Rightarrow w=\sum_{i=1}^n \alpha_i y_i x_i \quad (6.37)\\ \frac{\partial L}{\partial b} &=0 \Rightarrow \sum_{i=1}^n \alpha_i y_i=0 \quad (6.38)\\ \frac{\partial L}{\partial \xi_i} &=0 \Rightarrow C-\alpha_i-r_i=0 \Rightarrow C = \alpha_i + \mu_i ,\quad i=1, \ldots, n \quad (6.39) \end{aligned} \]

　　将上面的关系式代入$L(w,b,\alpha,\xi,\mu) = \frac{1}{2}||w||^2 + C\sum \limits_{i=1}^m \xi_i + \sum \limits_{i=1}^m \alpha_i(1-\xi_i -y_i(w^Tx_i+b)) - \sum \limits_{i=1}^m \mu_i\xi_i$，
即可得到$\underset{w,b,\xi_i}{min} \frac{1}{2}||w||^2 + C\sum \limits_{i=1}^m \xi_i$的对偶问题。

\[\begin{align} &\underset{\alpha}{max} \sum \limits_{i=1}^m \alpha_i - \frac{1}{2} \sum \limits_{i=1}^m \sum \limits_{j=1}^m \alpha_i \alpha_j y_iy_jx_i^Tx_j \quad (6.40)\\ &\text{s.t} \sum \limits_{i=1}^m \alpha_i y_i = 0 \\ &0 ≤ \alpha_i　≤ C, i=1,2,...,m. \end{align} \]

式(6.40)的推导

式(6.40)的推导
其实按步就班地按6.2节推导也能得到式(6.40)的优化目标，这里提一种直观方法。
将式(6.36)分成两个部分：与$\xi_i$有关的项和与$\xi_i$无关的项，即

$L(w,b,\alpha, \xi, \mu) = \frac{1}{2}||w||^2 + C\sum \limits_{i=1}^m \xi_i + \sum \limits_{i=1}^m \alpha_i(1 - \xi_i - y_i(w^Tx_i + b)) - \sum \limits_{i=1}^m \mu_i \xi_i \\ = \left(\frac{1}{2}||w||^2 + \sum \limits_{i=1}^m \alpha_i (1 - y_i(w^Tx_i + b)) \right) + \left(C\sum \limits_{i=1}^m \xi_i - \sum \limits_{i=1}^m \alpha_i\xi_i -\sum \limits_{i=1}^m \mu_i \xi_i \right)\\= \left( \frac{1}{2}||w||^2 + \sum \limits_{i=1}^m \alpha_i(1 - y_i(w^Tx_i + b))\right) + \sum \limits_{i=1}^m (C-\alpha_i -\mu_i)\xi_i$.
根据式(6.39)可知$C - \alpha_i - \mu_i = 0$，式(6.36)仅剩
$L(w, b, \alpha, \xi, \mu) = \frac{1}{2}||w||^2 + \sum \limits_{i=1}^m \alpha_i(1 - y_i(w^Tx_i + b))$.
即与式(6.8)相同，而式(6.37)(6.38)分别与式(6.9)(6.10)相同，因此代入后所得式(6.40)目标函数与式(6.11)目标函数亦相同。至于约束条件，由$C = \alpha_i + \mu_i$和$\alpha_i>0，\mu_i>0$，很容易得到$0 \leq \alpha_i \leq C$。

对软间隔支持向量机，KKT条件要求

\[\left\{\begin{matrix} \alpha_i≥0,\quad \mu_i≥0, \\ y_if(x_i)-1+\xi_i≥0， \\ \alpha_i(y_i(f(x_i)-1+\xi_i) = 0,\\ \xi_i≥0,\quad \mu_i \xi_i = 0 \end{matrix}\right. \quad \quad (6.41) \]

　　于是，对任意训练样本$(x_i,y_i)$，总有$\alpha_i=0$或$y_if(x_i) = 1- \xi_i$。
　　若$\alpha_i = 0$，则该样本不会对$f(x)$有任何影响；若$\alpha_i>0$，则必有$y_if(x_i) = 1 -\xi_i$，即该样本是支持向量：
　　由$C = \alpha_i + \mu_i$可知，若$\alpha_i<C$，则$\mu_i>0$，进而有$\xi_i=0$，即该样本落在最大间隔内部，若$\xi_i>1$，则该样本被错误分类。

　　由此可看出，软间隔支持向量机的最终模型仅与支持向量有关，即通过采用hinge损失函数仍保持了稀疏性。

对率回归与支持向量机的关系

　　在第 132 页最后一段,讨论了对率回归与支持向量机的关系,提到“如果使用对率损失$\ell_{log}$来替代式(6.29)中的0/1损失函数，,则几乎就得到了对率回归模型(3.27)” ,但式(6.29)与文中所提到的第三章对率回归模型式(3.27)形式上相差甚远。为了更清晰的说明对率回归与软间隔支持向量机的关系,以下先对式(3.27)的形式进行变化。

　　将$\beta = (w;b)$和$\hat x = (x;1)$代入式(3.27)：

\[\begin{align} & \ell(w,b) = \sum \limits_{i=1}^m \left(-y_i(w^Tx_i + b) + ln\left(1 + e^{w^Tx_i + b} \right)\right) \\ & = \sum \limits_{i=1}^m \left(ln\frac{1}{e^{y_i}(w^Tx_i + b)} + ln \left(1 + e^{w^Tx_i+b} \right) \right) \\ & = \sum \limits_{i=1}^m ln(\frac{1 + e^{w^Tx_i + b}}{e^{y_i}(w^Tx_i + b)}) \\ & = \left\{\begin{matrix} \sum_{i=1}^m ln(1 + e^{-(w^Tx_i + b)}),\quad y_i = 1 \\ \sum_{i=1}^m ln(1 + e^{w^Tx_i + b}), \quad y_i = 0 \end{matrix}\right. \end{align} \]

上式中，正例和反例分别用$y=1$和$y=0$分别表示，这是对率回归中的管理；而在支持向量机中正例和反例习惯用$y = +1$和$y = -1$表示。实际上，若用$y = +1$和$y = -1$分别表示正例和反例，上式可以表示成如下：
$\ell(w,b) = \sum \limits_{i=1}^m ln(1 + e^{-y_i(w^Tx_i + b)}) \\ = \left\{\begin{matrix} \sum_{i=1}^m ln(1 + e^{-(w^Tx_i + b)}), \quad y_i = +1\\ \sum_{i=1}^m ln(1 + e^{w^Tx_i + b}, \quad y_i = -1)\end{matrix}\right.$

即以上两个公式等价，而上式求和项正是式(6.33)表述的对率损失。
书中图6.5中的$0/1$损失、hinge损失、对率损失如下图所示：

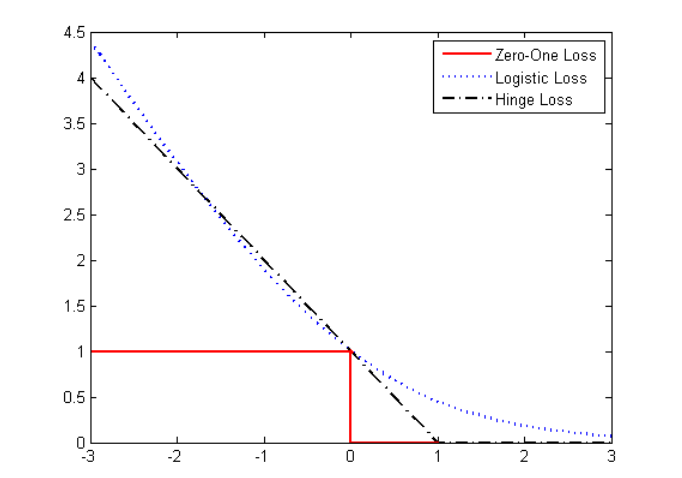
为了保正对率损失函数通过固定点 ,实际画的是以 2 为底的对数,根据换底公式,这与以自然常数 e 为底的对数只相差一个固定的倍数,而这在优化目标中并无实质影响:
$\ell_{log}(z) = log_2(1 + exp(-z)) = \frac{1}{ln2}(1 + exp(-z))$.
现在使用对率损失函数$\ell_{log}$来替代式(6.29)中的$0/1$损失函数
$\min \limits_{w,b} \frac{1}{2}||w||^2 + C\sum \limits_{i=1}^m log(1 + e^{-y_i(w^Tx_i + b)})$.
　　上式实际上就是带有正则化(regularization)的对率回归模型，按当前符号换为Andrew Ng在Coursera上的机器学习课程中的对率回归优化目标表达方式$\min \limits_{w,b} \sum \limits_{i=1}^m log(1 + e^{-y_i(w^Tx_i + b)}) + \frac{\lambda}{2m}||w||^2$.
　　通过以上推导可以得出结论：对率回归与软间隔支持向量机本质相同，区别仅在于代价函数不同。对率回归从最大似然概率(或最小化分类代价)角度入手，为防止过拟合在目标函数中引入正则化项$||w||^2$;而支持向量机则从最大间隔角度入手，为了允许部分样本分类出错在目标函数中引入损失函数，若将损失函数取为对率损失，则软间隔支持向量机即为对率回归，但软间隔支持向量机却巧妙地使用了Hinge损失，进而保留了硬间隔支持向量机中支持向量的概念，在式(6.6)的解释中已经提到最大化间隔相当于寻找最不可能过拟合的分类超平面，这就是正则化的目标。

2.2 正则化

　　我们还可以把式$\underset{w,b}{min} \frac{1}{2}||w||^2 + C\sum \limits_{i=1}^m max(0,1-y_i(w^Tx_i+b))$中的0/1损失函数换成别的替代损失函数以得到其他学习模型，这些模型的性质与所用的替代函数直接相关，但它们具有一个共性：优化目标中的第一项用来描述划分超平面的“间隔”大小，另一项$\sum_{i=1}^m \ell(f(x_i),y_i)$用来表述训练集上的误差，可写为更一般的形式

\[\underset{f}{min}\varOmega f(x) + C \sum \limits_{i=1}^m \ell(f(x_i),y_i) \]

　　其中$\varOmega(f)$称为“结构风险”(structural risk)，用于描述模型$f$的某些性质；
　　第二项$\sum_{i=1}^m\ell(f(x_i),y_i)$称为“经验风险”(empirical risk)，用于描述模型与训练数据的契合程度；
　　$C$用于二者折中。从经验风险最小化的角度来看，$\varOmega(f)$表述了我们希望获得具有何种性质的模型(例如希望获得复杂度较小的模型)，这为引入领域知识和用户意图提供了途径；
　　
另一方面，该信息有助于削减假设空间，从而降低了最小化训练误差的过拟合风险，从这个角度来说

\[\underset{f}{min}\varOmega f(x) + C \sum \limits_{i=1}^m \ell(f(x_i),y_i) \]

称为“正则化”(regularization)问题，$\varOmega(f)$称为正则化项，$C$则称为正则化常数。
$L_p$范数(norm)是常用的正则化项，其中$L_2$范数$||w||_2$倾向于$w$的分量取值均衡，即非零分量个数尽量稠密，而$L_0$范数$||w||_0$和$L_1$范数$||w||_1$则倾向于$w$的分量尽量稀疏，即非零分量个数尽量少。

2.3 支持向量回归(SVR)

　　根据前面的讨论，我们知道，优化目标可写为$\underset{w,b}{min} \frac{1}{2}||w||^2 + C\sum \limits_{i=1}^m\ell_{0/1}(y_i(w^Tx_i+b)-1$。
　　那么，能否对$\underset{w,b}{min} \frac{1}{2}||w||^2 + C\sum \limits_{i=1}^m\ell_{0/1}(y_i(w^Tx_i+b)-1$使用其他的替代损失函数呢？
　　可以发现，如果使用对率损失函数$\ell_{log}$来替代式中的$0/1$损失函数，则几乎就得到了对率回归模型。

　　另一方面，从上图可看出,hinge损失有一块“平坦”的零区域，这使得支持向量机的解具有稀疏性，而对率损失是光滑的单调递减函数，不能导出类似支持向量的概念，因此对率回归的解依赖于更多的训练样本，其预测开销更大。

　　下面我们考虑回归问题。
　　给定训练样本$D=\left\{(x_1,y_1),(x_2,y_2),...,(x_m,y_m)\right\},y∈\mathbb{R}$，希望学得一个形如$f(x) = w^Tx+b$的回归模型，使得$f(x)$与$y$尽可能接近，$w$和$b$是待确定的模型参数。

　　对样本$(x,y)$，传统回归模型通常直接基于模型输出$f(x)$与真实输出$y$之间的差别来计算损失，当且仅当$f(x)$与$y$完全相同时，损失才为零。与此不同，在支持向量回归(Support Vector Regression，简称SVR)模型中，我们假设能容忍$f(x)$与$y$之间最多有$\epsilon$的偏差，即仅当$f(x)$与$y$之间的差别绝对值大于$\epsilon$时才计算损失。

　　如下图所示，这相当于以$f(x)$为中心，构建了一个宽度为$2\epsilon$的间隔带，若训练样本落入此间隔待，则被认为是预测正确的。　

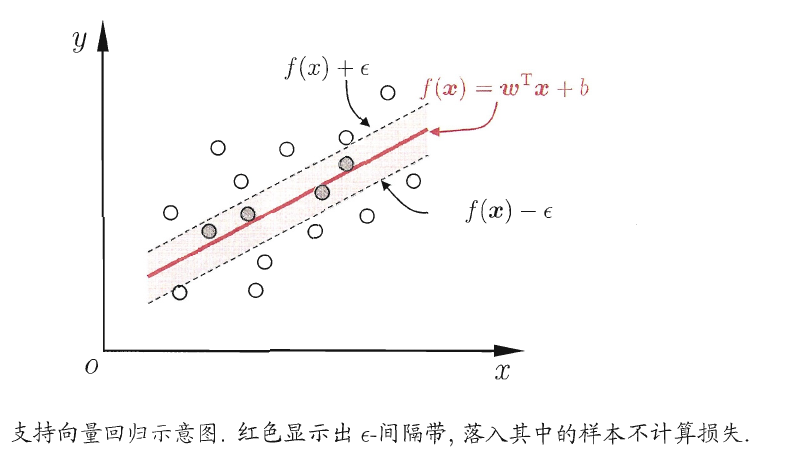
于是，支持向量回归SVR问题可形式化为

\[\underset{w,b}{min} \frac{1}{2} ||w||^2 + C\sum \limits_{i=1}^m\ell_{\epsilon}(f(x_i) - y_i) \quad \quad (6.43) \]

其中Ｃ为正则化常数，$\ell_{\epsilon}$是下图所示的$\epsilon$-不敏感损失($\epsilon$-insensitive)函数。

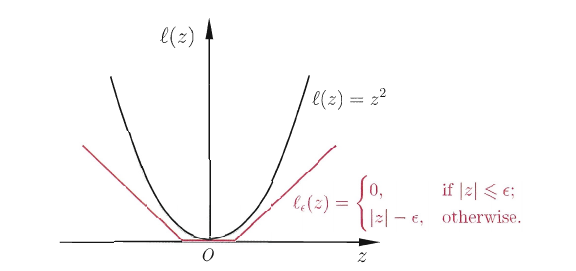
\[\ell_{\epsilon}(z) = \left\{\begin{matrix} 0 ,\quad if|z| \leq \epsilon \\ |z|-\epsilon,\quad otherwise \end{matrix}\right. \quad \quad (6.44) \]

引入松弛变量$\xi_i$和$\hat \xi_i$，可将(6.43)$\underset{w,b}{min} \frac{1}{2} ||w||^2 + C\sum \limits_{i=1}^m\ell_{\epsilon}(f(x_i) - y_i)$重写为

\[\begin{align} &\underset{w,b,\xi_i,\hat \xi_i}{min} \frac{1}{2}||w||^2 + Ｃ\sum \limits_{i=1}^m (\xi_i+\hat \xi_i) \quad \quad (6.45) \\ &\text{s.t}. \quad f(x_i) - y_i \leq \ \epsilon + \xi_i \\ &y_i - f(x_i) \leq \epsilon + \hat \xi_i \\ &\xi_i \geq 0, \quad \hat \xi_i \geq 0, \quad i=1,2,...,m \end{align} \]

式(6.45)的解释

类似于式(6.35)的解释，对于任意$x_i$，$f(x_i) - y_i \leq \epsilon + \xi_i$和$y_i - f(x_i) \leq \epsilon + \hat \xi_i$两个约束条件一定有其一成立，因为$f(x_i) - y_i$和$y_i - f(x_i)$一定有其一小于等于零，因此两个松弛变量$\xi_i$和$\hat \xi_i$之中定有一个等于零。

类似$L(w,b,\alpha,\xi,\mu) = \frac{1}{2}||w||^2 + C\sum \limits_{i=1}^m \xi_i + \sum \limits_{i=1}^m \alpha_i(1-\xi_i -y_i(w^Tx_i+b)) - \sum \limits_{i=1}^m \mu_i\xi_i$，通过引入拉格朗日乘子$\mu_i \geq 0,\hat \mu_i \geq 0,\alpha_i \geq 0, \hat \alpha_i \geq 0$，由拉格朗日乘子法可得到$\underset{w,b,\xi_i,\hat \xi_i}{min} \frac{1}{2}||w||^2 + Ｃ\sum \limits_{i=1}^m (\xi_i+\hat \xi_i)$的拉格朗日函数，如下

\[\begin{align} &L(w,b,\alpha,\hat \alpha, \xi, \hat \xi, \mu, \hat \mu) \\ &= \frac{1}{2}||w||^2 + C\sum \limits_{i=1}^m (\xi_i - \hat \xi_i) - \sum \limits_{i=1}^m\mu_i \xi_i - \sum \limits_{i=1}^m \hat \mu_i \hat \xi_i + \\ &\sum \limits_{i=1}^m \alpha_i(f(x_i)-y_i-\epsilon-\xi_i) + \sum \limits_{i=1}^m \hat \alpha_i(y_i - f(x_i) - \epsilon - \hat \xi_i) \end{align} \quad \quad (6.46) \]

式(6.46)的解释

由于式(6.45)是最小化目标函数，因此引入拉格朗日乘子时要将所有不等式约束转化为小于等于零的形式，所以针对$\xi_i$和$\hat \xi_i$的两项前面的符号是负号。

将$f(x)=w^Tx+b$代入，再令$L(w,b,\alpha,\hat \alpha,\xi,\hat \xi, \mu,\hat \mu)$对$w,b,\xi_i$和$\hat \xi_i$的偏导为零，可得

\[\begin{align} &\frac{\partial L}{\partial w}= 0 \Rightarrow w = \sum \limits_{i=1}^m (\hat \alpha_i - \alpha)x_i \quad (6.47) \\ &\frac{\partial L}{\partial b}= 0 \Rightarrow 0 = \sum \limits_{i=1}^m (\hat \alpha_i - \alpha) \quad (6.48) \\ &\frac{\partial L}{\partial \xi_i}= 0 \Rightarrow C = \alpha_i + \mu_i \quad (6.49) \\ &\frac{\partial L}{\partial \hat \xi_i}= 0 \Rightarrow C = \hat \alpha_i + \hat \mu_i \quad (6.50) \\ \end{align} \]

式(6.47)的解释

$\frac{\partial L(w,b,\alpha, \hat \alpha, \xi, \hat \xi, \mu, \hat \mu)}{\partial w} = w + \sum \limits_{i=1}^m \alpha_i x_i - \sum \limits_{i=1}^m \hat \alpha_i x_i$.
令偏导等于零即可得式(6.47).
同理可得式(6.48)(6.49)(6.50)，注意求偏导时，所有不含求导变量的变量统一舍去。

将上面的关系式代入拉格朗日函数$L(w,b,\alpha,\hat \alpha, \xi, \hat \xi, \mu, \hat \mu) \\＝ \frac{1}{2}||w||^2 + C\sum \limits_{i=1}^m (\xi_i - \hat \xi_i) - \sum \limits_{i=1}^m\mu_i \xi_i - \sum \limits_{i=1}^m \hat \mu_i \hat \xi_i \\+ \sum \limits_{i=1}^m \alpha_i(f(x_i)-y_i-\epsilon-\xi_i) + \sum \limits_{i=1}^m \hat \alpha_i(y_i - f(x_i) - \epsilon - \hat \xi_i) \quad(6.46)$
即可得到SVR的对偶问题

\[\begin{align} & \underset{\alpha,\hat \alpha}{max} \sum \limits_{i=1}^m y_i(\hat \alpha_i - \alpha_i) -\epsilon(\hat \alpha_i + \alpha_i) - \frac{1}{2} \sum \limits_{i=1}^m \sum \limits_{j=1}^m (\hat \alpha_i - \alpha_i)(\hat \alpha_j - \alpha_j)x_i^Tx_j \quad (6.51)\\ & \text{s.t}. \quad \sum \limits_{i=1}^m(\hat \alpha_i - \alpha_i) = 0 \\ & 0 \leq \alpha_i, \quad \hat \alpha_i \leq C \end{align} \]

式(6.51)的推导

首先将式(6.46)所有与$\xi_i$和$\hat \xi_i$有关项进行整合(第$2~4$项及$5~6$项中的一部分):
$C\sum_{i=1}^m (\xi_i + \hat \xi_i) - \sum_{i=1}^m \mu_i\xi_i - \sum_{i=1}^m \hat \mu_i \xi_i - \sum_{i=1}^m \alpha_i \xi_i - \sum_{i=1}^m \hat \alpha_i \hat \xi_i \\ =C\sum_{i=1}^m(\xi_i+\hat \xi_i) - \sum_{i=1}^m (\mu_i + \alpha_i)\xi_i - \sum_{i=1}^m(\hat \mu_i + \hat \alpha_i)\hat \xi_i$.

将式(6.49)和(6.50)代入得：
$= C\sum_{i=1}^m (\xi_i + \hat \xi_i) - \sum_{i=1}^m C\xi_i - \sum_{i=1}^m C\hat \xi_i\\ = C\sum_{i=1}^m (\xi_i + \hat \xi_i) -C\sum_{i=1}^m \xi_i - C\sum_{i=1}^m \hat \xi_i = 0$.
然后将式(6.46)所有与$\epsilon$有关项进行整合(第$5\sim6$项中的一部分):
$-\sum_{i=1}^m \alpha_i \epsilon - \sum_{i=1}^m \hat \alpha_i \epsilon = -\sum_{i=1}^m \epsilon(\hat \alpha_i + \alpha_i)$.
接下来将式(6.46)所有与$y_i$有关项进行整合(第$5\sim 6$项中的一部分)：
$-\sum_{i=1}^m \alpha_i y_i + \sum_{i=1}^m \hat \alpha_i y_i = \sum_{i=1}^m y_i(\hat \alpha_i - \alpha_i)$.
到此为止，式(6.46)未处理的三项分别是$\frac{1}{2}||w||^2、\sum_{i=1}^m \alpha_if(x)$和$-\sum_{i=1}^m \hat \alpha_if(x_i)$，由式(6.7)的$f(x_i) = w^Tx_i + b$代入：
$\sum_{i=1}^m \alpha_i f(x_i) - \sum_{i=1}^m \hat \alpha f(x_i) \\ = \sum_{i=1}^m(\alpha_i - \hat \alpha_i)(w^Tx_i + b) \\ = \sum_{i=1}^m (\alpha_i - \hat \alpha_i)(w^Tx_i) + \sum_{i=1}^m (\alpha_i - \hat \alpha_i)b \\= -w^T\sum_{i=1}^m (\hat \alpha_i - \alpha_i)x_i - b \sum_{i=1}^m (\hat \alpha_i - \alpha_i)$.
根据式(6.48)上式后一项等于0。
将式(6.47)代入上式第一项: $=-w^Tw$.
综合以上结果：
$L(w,b,\alpha,\hat \alpha,\xi, \hat \xi_i, \mu, \hat \mu) = \frac{1}{2}||w||^2 - w^Tw + \sum_{i=1}^m y_i(\hat \alpha_i - \alpha_i) - \sum_{i=1}^m \epsilon (\hat \alpha_i + \alpha_i) \\ = \sum_{i=1}^m (y_i(\hat \alpha_i - \alpha_i) - \epsilon(\hat \alpha_i + \alpha_i)) - \frac{1}{2}||w||^2$.
将式(6.47)代入$\frac{1}{2}||w||^2$.
$\frac{1}{2}||w||^2 = \frac{1}{2}w^Tw = \frac{1}{2}(\sum_{i=1}^m (\hat \alpha_i - \alpha_i)x_i)^T(\sum_{i=1}^m (\hat \alpha_i - \alpha_i)x_i) \\ =\frac{1}{2}\sum_{i=1}^m \sum_{j=1}^m (\hat \alpha_i - \alpha_i)(\hat \alpha_j - \alpha_j)x_i^Tx_j$.
代入前面的$L(w,b,\alpha,\hat \alpha, \xi, \hat \xi, \mu, \hat \mu)$推导结果即可得式(6.51)。
由于$\alpha_i \geq 0,\hat \alpha \geq 0, \mu_i \geq ,\hat \mu_i \geq 0$，结合式(6.49)(6.50)即可得约束$0 \leq \alpha_i, \hat \alpha_i \geq C$.

上述过程中需满足KKT条件，即要求

\[\left\{\begin{matrix} \alpha_i(f(x_i) - y_i - \epsilon - \xi_i) = 0 \\ \hat \alpha_i(y_i - f(x) - \epsilon - \hat \xi_i) = 0 \\ \alpha_i \hat \alpha_i = 0, \quad \xi_i \hat \xi_i = 0 \\ (C-\alpha_i)\xi_i = 0, \quad (C-\hat \alpha_i)\hat \xi_i = 0 \end{matrix}\right. \quad \quad (6.52) \]

式(6.52)的解释

完整的KKT条件是(每三个一组，对应于某一类不等式约束):
$\left\{\begin{matrix} f(x_i) - y_i - \epsilon -\xi_i \leq 0 \\ \alpha_i \geq 0 \\ \alpha_i(f(x_i) - y_i - \epsilon - \xi_i) = 0\end{matrix}\right.$ (式(6.52)第一行式子)

$\left\{\begin{matrix} y_i - f(x_i) - \epsilon - \hat \xi_i \\ \hat \alpha_i \geq 0 \\ \hat \alpha_i(y_i- f(x_i) - \epsilon - \hat \xi_i) = 0 \end{matrix}\right.$ (式(6.52)第二行式子)

$\left\{\begin{matrix} y_i - f(x_i) - \epsilon - \hat \xi_i \\ \hat \alpha_i \geq 0 \\ \hat \alpha_i(y_i- f(x_i) - \epsilon - \hat \xi_i) = 0 \end{matrix}\right.$ (式(6.52)第二行式子)

$\left\{\begin{matrix} \xi_i \geq 0 \\ \mu_i \geq 0 \\ \hat \mu_i \hat \xi_i = 0 \end{matrix}\right.$ (式(6.52)第四行左侧式子)

$\left\{\begin{matrix} \hat \xi_i \geq 0 \\ \hat \mu_i \geq 0 \\ \hat \mu_i \hat \xi_i = 0 \end{matrix}\right.$ (式(6.52)第四行右侧式子)

如式(4.45)的解释，两个松弛变量$\xi_i$和$\hat \xi_i$必定有其中之一等于零，即为式(6.52)第三行右侧式子。
如式(6.52)下面一段话的叙述，仅当样本$(x_i, y_i)$不落于$\epsilon$间隔带中，相应的$\alpha_i$和$\hat \alpha_i$才能取非零值，而$f(x_i) - y_i - \epsilon - \xi_i = 0$和$y_i - f(x_i) - \epsilon -\hat \xi_i = 0$分别代表样本$(x_i, y_i)$落在间隔带外的某一侧，但这不可能同时发生(如图6.6所示，一个样本不可能同时位于间隔带外的左上方和右下方)，因此$\alpha_i$和$\hat \alpha_i$中至少有一个为零(如果样本就在间隔带内部则二者同时为零)，即式(6.52)第三行左侧式子。

可以看出，当且仅当$f(x_i) - y_i - \epsilon - \xi_i = 0$时，$\alpha_i$能取非零值，当且仅当$y_i-f(x_i)-\epsilon-\hat \xi_i = 0$时，$\hat \alpha_i$能取非零值。换言之，仅当样本$(x_i,y_i)$不落入$\epsilon$间隔带中，相应的$\alpha_i$和$\hat \alpha_i$才能取非零值。此外，约束$f(x_i) - y_i - \epsilon - \xi_i = 0$和$y_i-f(x_i)-\epsilon-\hat \xi_i = 0$不能同时成立，因此$\alpha_i$和$\hat \alpha_i$中至少有一个为零。

　　将$w = \sum \limits_{i=1}^m (\hat \alpha_i - \alpha)x_i\quad(6.47)$代入$f(x)=w^Tx+b \quad (6.7)$，则SVR的解形如

\[f(x) = \sum \limits_{i=1}^m (\hat \alpha_i - \alpha_i)x_i^Tx + b \quad \quad (6.53) \]

式(6.53)的解释

如式(6.52)的解释所述，$\alpha_i$和$\hat \alpha_i$中至少有一个为零，若二者都为零，即样本在间隔带内部，则不出现在式(6.53)中；若二者有一个不为零(且最多有一个不为零)，即样本在间隔带外部，则出现在式(6.53)中，即为SVR支持向量回归SVR的支持向量。即“显然，SVR的支持向量仅是训练样本的一部分，即其解仍具有稀疏性”，而之所以其解具有稀疏性就是因为SVR的代价函数(如图6.7红线)有一段零值区域，而不像线性回归一样，代价函数是平方损失(如图6.7黑线).　　

　　能使上式中的$(\hat \alpha_i - \alpha_i)\neq0$的样本即为SVR的支持向量，它们必落在$\epsilon-$间隔带之外。显然，SVR的支持向量仅是训练样本的一部分，即其解仍具有稀疏性。

　　由KKT条件(6.52)可看出，对每个样本$(x_i,y_i)$都有$(C-\alpha_i)\xi_i=0$且$\alpha_i(f(x_i)-y_i-\epsilon-\xi_i)＝0$.于是，在得到$\alpha_i$后，若$0<\alpha_i<C$，则必有$\xi_i=0$，进而有

\[b = y_i + \epsilon - \sum \limits_{i=1}^m(\hat \alpha_i - \alpha_i)x_i^Tx \quad (6.54) \]

式(6.54)的推导

若$0 < \alpha_i < C$，则$\mu_i = C - \alpha_i \neq 0$，由KKT条件$\mu_i \xi_i = 0$则必有$\xi_i = 0$;
再有KKT条件$\alpha_i(f(x_i) - y_i - \epsilon - \xi_i) = 0$，由于$\alpha_i \neq 0$则必有$f(x_i) - y_i - \epsilon - \xi_i = 0$；考虑刚才得到的$\xi_i = 0$再加之$f(x_i) = w^Tx_i + b$，即$w^Tx_i + b - y_i - \epsilon = 0$，故$b = y_i + \epsilon + w^Tx_i$，再将式(6.47)代入替换$w$，即可得式(6.54)。

因此，在求解SVR对偶问题后得到$\alpha_i$后，理论上来说，可任意选取满足$0<\alpha_i<Ｃ$的样本通过$b = y_i + \epsilon - \sum \limits_{i=1}^m(\hat \alpha_i - \alpha_i)x_i^Tx \quad (6.54)$求得$b$。
实践中，常用一种更鲁棒的办法：选取多个(或所有)满足条件$0<\alpha_i<C$的样本求解$b$后取平均值。

若考虑特征映射形式$f(x) = w^T\phi(x)+b \quad (6.19)$，则相应的，$w = \sum \limits_{i=1}^m (\hat \alpha_i - \alpha)x_i \quad (6.47)$将形如

\[w = \sum \limits_{i=1}^m (\hat \alpha_i - \alpha_i)\phi(x_i) \quad (6.55) \]

将上式代入特征映射形式$f(x) = w^T\phi(x)+b$，则SVR可表示为

\[f(x) = \sum \limits_{i=1}^m (\hat \alpha_i - \alpha_i)\kappa(x,x_i) + b　\\ = \sum \limits_{i=1}^m (\hat \alpha_i - \alpha_i) \left[\phi(x_i)^T\phi(x_j) \right] + b \]

其中$\kappa(x_i,x_j) = \phi(x_i)^T\phi(x_j)$为核函数。

SVR(支持向量回归)与SVM(支持向量机)的区别

首先，从功能和作用上看，SVR是用来做回归任务的，SVM是用来做分类任务的；
回归任务是希望一条直线(超平面)使得更多的点落在这条直线上，而分类任务是希望有一条直线(或超平面)将不同类别的点一分为二。
比较式(6.43)和(6.34)可以知道，二者的主要区别就在于代价函数(Cost Function)，这也是回归任务和分类任务的本质决定的，SVR的代价函数是希望更多的点落在$\epsilon$间隔带，SVM的代价函数是希望更多的点满足$y_i(w^Tx_i+b)>1$，因为此时代价函数为零，这也是SVR区别于线性回归、SVM区别于对率回归的最本质指出，正是因为代价函数有零值区域才导致了“支持向量”的概念(支持向量就是使代价函数非零的点)，而线性回归和对率回归的代价函数均为非零函数，故不能导出支持向量概念(或者是所有训练样本都是支持向量)。

(三)核方法

我们在这里回顾前面的讨论，由上面的推导已经得到下面两个模型表示形式
SVM支持向量机模型　$f(x) = \sum \limits_{i=1}^m \alpha_i y_i \kappa(x,x_i) + b$
SVR支持向量回归模型　$f(x) = \sum \limits_{i=1}^m (\hat \alpha_i - \alpha_i)\kappa(x,x_i) + b$
若不考虑偏移项$b$，则无论SVM还是SVR，学得的模型总能表示成核函数$\kappa(x,x_i)$的线性组合。

基于以上事实，将其推广至一般情况，可得结论:

3.1 Th 表示定理

令$\mathbb{H}$为核函数$\kappa$对应的再生核希尔伯特空间，$||h||_{\mathbb{H}}$表示$\mathbb{H}$空间中关于$h$的范数，对于任意单调递增函数$\Omega:[0,\infty] \longmapsto\mathbb{R}$和任意非负损失函数$\ell:\mathbb{R^m}\longmapsto[0,\infty]$，优化问题

\[\underset{h∈\mathbb{H}}{min} F(h) = \Omega(||h||_{\mathbb{H}}) + \ell(h(x_1),h(x_2),...,h(x_m)) \quad \quad (6.57) \]

的解总可写为

\[h^*(x) = \sum \limits_{i=1}^m \alpha_i \kappa(x,x_i) \quad \quad (6.58) \]

Th表示定理的说明

式(6.24)是式(6.20)的解；式(6.56)是式(6.43)的解。
对应到表示定理式(6.57)当众，式(6.20)和式(6.43)均为$\Omega(||h||_{\mathbb{H}}) = \frac{1}{2}||w||^2$；式(6.20)的$\ell(h(x_1), h(x_2),...,h(x_m)) = 0$，而式(6.43)的$\ell(h(x_1), h(x_2),...,h(x_m)) = C\sum_{i=1}^m \ell_{\epsilon}(f(x_i) - y_i)$;即均满足式(6.57)的要求，式(6.20)和式(6.43)的解$f(x)$均为$\kappa(x, x_i)$的线性组合，即式(6.58)。

表示定理对损失函数没有限制，对正则化项$\Omega$仅要求单调递增，甚至不要求$\Omega$是凸函数，意味着对于一般的损失函数和正则化项，优化问题$\underset{h∈\mathbb{H}}{min} F(h) = \Omega(||h||_{\mathbb{H}}) + \ell(h(x_1),h(x_2),...,h(x_m))$的最优解$h^*(x)$都可表示为核函数$\kappa(x,x_i)$的线性组合。

　　我们将一系列基于核函数的学习方法，统称为“核方法”(kernel methods)。最常见的，是通过“核化”(即引入核函数)来将线性学习器拓展为非线性学习器，从而得到“核线性判别分析”(Kernelized Linear Discriminant Analysis，简称KLDA)。

　　我们先假设可通过某种映射$\phi$:$\mathcal{X} \longmapsto \mathbb{F}$将样本映射到一个特征空间$\mathbb{F}$，然后在$\mathbb{F}$中执行线性判别分析，以求得

\[h(x) = w^T\phi(x) \quad (6.59) \]

类似于(3.35)，KLDA的学习目标是

\[\underset{w} {max}J(w) = \frac{w^T S_b^{\phi} w}{w^T S_w^{\phi} w} \quad (6.60) \]

其中$S_b^{\phi}$和$S_w^{\phi}$分别为训练样本在特征空间$\mathbb{F}$中的类间散度矩阵和类内矩阵。令$X_i$表示第$i$∈{0,1}类样本的集合，其样本数为$m_i$；总样本数$m = m_0 + m_1)$。第$i$类样本在特征空间$\mathbb{F}$的均值为

\[\mu_i^{\phi} = \frac{1}{m_i} \sum \limits_{x∈X_i}\phi(x) \quad (6.61) \]

两个散度矩阵分别为

\[\begin{align} &S_b^{\phi} = (\mu_1^{\phi} - \mu_0^{\phi})(\mu_1^{\phi} - \mu_0^{\phi})^T \quad (6.62)\\ &S_w^{\phi} = \sum \limits_{i=0}^1 \sum \limits_{x∈X_i}(\phi(x)-\mu_i^{\phi})(\phi(x)-\mu_i^{\phi})^T \quad (6.63) \end{align} \]

通常我们难以知道映射$\phi$的具体形式，因此使用核函数$\kappa(x,x_i) = \phi(x_i)^T\phi(x)$来隐式地表达这个映射和特征空间$\mathbb{F}$。把$J(w)$作为优化问题$\underset{h∈\mathbb{H}}{min} F(h) = \Omega(||h||_{\mathbb{H}}) + \ell(h(x_1),h(x_2),...,h(x_m))$中的损失函数$\ell$，再令$\Omega=0$，由表示定理，函数$h(x)$可写为

\[h(x) = \sum \limits_{i=1}^m \alpha_i \kappa(x,x_i) \quad (6.64) \]

于是由$h(x) = w^T\phi(x)$可得

\[w = \sum \limits_{i=1}^m \alpha_i \phi(x_i) \quad (6.65) \]

令K∈$\mathbb{R}^{m×m}$为核函数$\kappa$所对应的核矩阵，$(K)_{ij} = \kappa(x_i,x_j)$。
令$1_{i}$∈$\left\{1,0\right\}^{m×1}$为第$i$类样本的指示向量，即$1_{i}$的第$j$个分量为1当且仅当$x_j∈X_i$，否则$1_{i}$的第$j$个分量为0。
再令

\[\begin{align} &\hat \mu_0 = \frac{1}{m_0}K1_0 , \quad (6.66)\\ &\hat \mu_1 = \frac{1}{m1}K1_1, \quad (6.67)\\ &M = (\hat \mu_0 - \hat \mu_1)(\hat \mu_0 - \hat \mu_1)^T, \quad (6.68)\\ &N = KK^T - \sum \limits_{i=0}^1 m_1 \hat \mu_i \hat \mu_i^T \quad (6.69) \end{align} \]

于是KLDA的学习目标$\underset{w} {max}J(w) = \frac{w^T S_b^{\phi} w}{w^T S_w^{\phi} w}$等价于

\[\underset{\alpha} {max}J(\alpha) = \frac{\alpha^T M \alpha}{\alpha^T N \alpha} \quad (6.70) \]

显然，使用线性判别分析求解方法即可得到$\alpha$，进而可由$h(x) = \sum \limits_{i=1}^m \alpha_i \kappa(x,x_i)$得到投影函数$h(x)$。

式(6.70)的推导

式(6.70)实际就是用式(6.65)的$w$替换式(6.60)，化简可得：
(1)先化简分子部分，将式(6.61)代入式(6.62)，再将式(6.62)和式(6.65)代入分子
$w^TS_{b}^{\phi}w = \left(\sum \limits_{i=1}^m \alpha_i \phi(x_i) \right)^T \cdot \left(\frac{1}{m} \sum \limits_{x \in X_1} \phi(x) - \frac{1}{m_0} \sum \limits_{x \in X_0} \phi(x) \right) \\\cdot \left(\frac{1}{m_1} \sum \limits_{x \in X_1}\phi(x) - \frac{1}{m_0}\sum \limits_{x \in X_0} \phi(x) \right)^T \cdot \left(\sum \limits_{j=1}^m \alpha_j \phi(x_j) \right)$

先计算前两项矩阵的乘积：
$\left(\sum \limits_{i=1}^m \alpha_i \phi(x_i) \right)^T \cdot \left(\frac{1}{m_1} \sum \limits_{x \in X_1} \phi(x) - \frac{1}{m_0} \sum \limits_{x \in X_0} \phi(x) \right) \\ = \sum \limits_{i=1}^m \left(\alpha_i \phi(x_i)^T \cdot \left( \frac{1}{m_1} \sum \limits_{x \in X_1} \phi(x) - \frac{1}{m_0}\sum \limits_{x \in X_0} \phi(x)\right)\right)\\ = \sum \limits_{i=1}^m \alpha_i \left(\frac{1}{m_1}\sum \limits_{x \in X_1} \phi(x_i)^T\phi(x) - \frac{1}{m_0} \sum \limits_{x \in X_0} \phi(x_i)^T \phi(x) \right) \\ = \sum \limits_{i=1}^m \alpha_i \left(\frac{1}{m_1}\sum \limits_{x \in X_1} \kappa(x_i, x) - \frac{1}{m_0} \sum_{x \in X_0} \kappa(x_i, x) \right)$

同理，计算后两项矩阵的乘积：

$\left(\frac{1}{m_1} \sum \limits_{x \in X_1} \phi(x) - \frac{1}{m_0} \sum \limits_{x \in X_0}\phi(x) \right)^T \cdot \left(\sum \limits_{j=1}^m \alpha_j \phi(x_j) \right) \\ = \sum \limits_{j=1}^m \left(\frac{1}{m_1} \sum \limits_{x \in X_1} \kappa(x, x_j) - \frac{1}{m_0} \sum \limits_{x \in X_0} \kappa(x, x_j) \right)\alpha_j \\ =(\hat \mu_1 - \hat \mu_0)^T \alpha$

(2)再化简分母部分
为了方便推导，先拆解式(6.63)的$S_{w}^{\phi}$:
$S_{w}^{\phi} = \sum \limits_{i=1}^1 \sum \limits_{x \in X_i} \left(\phi(x)\phi(x)^T - \phi(x)(\mu_i^{\phi})^T - \mu_i^{\phi}\phi(x)^T + \mu_i^{\phi}(\mu_i^{\phi})^T \right) \\ = \sum \limits_{i=1}^1 \sum \limits_{x \in X_i} \phi(x)\phi(x)^T - \sum \limits_{i=1}^1 \sum \limits_{x \in X_i} \phi(x) (\mu_i^{\phi})^T - \sum \limits_{i=0}^1 \sum \limits_{x \in X_i} \mu_i^{\phi}(x)^T + \sum \limits_{i=1}^1 \sum \limits_{x \in X_i}\mu_i^{\phi}(\mu_i^{\phi})^T$

第一项：
$\sum \limits_{i=1}^1 \sum \limits_{x \in X_i}\phi(x) \phi(x)^T = \sum \limits_{x \in X_0}\phi(x)\phi(x)^T + \sum \limits_{x \in X_1}\phi(x)\phi(x)^T = \sum \limits_{x \in X}\phi(x) \phi(x)^T$

第二项：
$\sum \limits_{i=1}^1 \sum \limits_{x \in X_i} \phi(x) (\mu_i^{\phi})^T = \sum \limits_{x \in X_0}\phi(x)(\mu_o^{\phi})^T + \sum \limits_{x \in X_1}\phi(x)(\mu_1^{\phi})^T = m_0 \mu_0^{\phi}(\mu_0^{\phi})^T + m_1 \mu_1^{\phi}(\mu_1^{\phi})^T$

第三项：
$\sum \limits_{i=1}^1 \sum \limits_{x \in X_i} \mu_i^{\phi} \phi(x)^T = \sum \limits_{i=0}^1 \mu_i^{\phi} \sum \limits_{x \in X_i} \phi(x)^T \\ = \mu_0^{\phi} \sum \limits_{x \in X_0} \phi(x)^T + \mu_1^{\phi} \sum \limits_{x \in X_1}\phi(x)^T \\ = m_0 \mu_0^{\phi} + m_1 \mu_1^{\phi}(\mu_1^{\phi})$

第四项：

$\sum \limits_{i=1}^1 \sum \limits_{x \in X_i} \mu_i^{\phi} (\mu_i^{\phi})^T = \sum \limits_{x \in X_0} \mu_0^{\phi} (\mu_0^{\phi})^T + \sum \limits_{x \in X_1}\mu_1^{\phi}(\mu_1^{\phi})^T \\ = m_0\mu_0^{\phi}(\mu_0^{\phi})^T + m_1 \mu_1^{\phi}(\mu_1^{\phi})^T$

将第一项至第四项各自拆解结果代回到式(6.63)得最终$S_{w}^{\phi}$拆解结果：
$S_w^{\phi} = \sum \limits_{x \in X}\phi(x)\phi(x)^T - m_0\mu_0^{\phi}(\mu_0^{\phi})^T - m_1\mu_1^{\phi}(\mu_1^{\phi})^T$

将式(6.65)代入式(6.60)的分母，$S_w^{\phi}$按最终拆解结果分成三部分：
第一部分：

$\left(\sum \limits_{j=1}^m \alpha_j \phi(x_j) \right)^T \left(\sum \limits_{x \in X}\phi(x)\phi(x)^T \right) \left(\sum \limits_{k=1}^m \alpha_i \phi(x_k) \right) \\ = \sum \limits_{j=1}^m \sum \limits_{x \in X} \sum \limits_{k=1}^m (\alpha_i \phi(x_j)^T \phi(x)\phi(x)^T \alpha_k \alpha(x_k)) \\ = \sum \limits_{j = 1}^m \sum \limits_{x \in X} \sum \limits_{k=1}^m (\alpha_j \kappa(x_j, x)\alpha_k \kappa(x, x_k)) \\ = \alpha^T KK^T \alpha$

第二部分：

$\left(\sum \limits_{j=1}^m \alpha_j \phi(x_j) \right)^T \left(m_0 \mu_0^{\phi}(\phi_0^{\phi})^T\right) \left(\sum \limits_{k=1}^m \alpha_k \phi(x_k) \right) \\ = \left(\sum \limits_{j=1}^m \alpha_j \phi(x_j)\right)^T \left(m_0 \cdot \frac{1}{m_0} \sum \limits_{x \in X_0} \phi(x) \cdot \frac{1}{m_0} \sum \limits_{x \in X_0} \phi(x)^T \right) \left(\sum \limits_{k = 1}^m \alpha_k \phi(x_k) \right) \\ = m_0 \cdot \frac{1}{m_0} \sum \limits_{j=1}^m \sum \limits_{x \in X_0} \alpha_j \phi(x_j)^T \phi(x) \cdot \frac{1}{m_0} \sum \limits_{x \in X_0} \sum \limits_{k=1}^m \alpha_k \phi(x)^T \phi(x_k) \\ =m_0 \cdot \frac{1}{m_0} \sum \limits_{j=1}^m \sum \limits_{x \in X_0} \alpha_j \kappa(x_j, x) \cdot \frac{1}{m_0} \sum \limits_{x \in X_0}\sum \limits_{k=1}^m \alpha_k \kappa(x, x_k) \\ = m_0 \alpha^T \hat \mu_0 \hat \mu_0^T \alpha$

第三部分：(与第二部分推导过程相同)

$\left(\sum \limits_{j=1}^m \alpha_j \phi(x_j)\right)^T \left(m_1 \mu_1^{\phi}(\mu_1^{\phi})^T \right) (\sum \limits_{k=1}^m \alpha_k \phi(x_k)) = m_1 \alpha^T \hat \mu_1 \mu_1^T \alpha$
将以上三部分的结果合并，并将式(6.69)代入

$w^T S_{w}^{\phi}w = \alpha^T KK^T \alpha - m_0 \alpha^T \hat \mu_0 \hat \mu_0^T\alpha - m_1 \alpha^T \hat \mu_1 \hat \mu_1^T \alpha \\ = \alpha^T(KK^T - m_0 \hat \mu_0 \hat \mu_0^T -m_1 \hat \mu_1 \hat \mu_1^T)\alpha \\ = \alpha^T(KK^T - \sum \limits_{i=0}^1 m_i \hat \mu_i \hat \mu_i^T) \alpha \\ = \alpha^T N \alpha$

综合以上分子分母的最终化简结果，即得式(6.70)

参考材料：
[1] 周志华《机器学习》
[2] 李航《统计学习方法》
[3] 邱锡鹏《神经网络与深度学习》

posted @ 2021-04-22 11:42 Xu_Lin 阅读(280) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

名称	表达式	参数
线性核	\(\kappa(x_i, x_j) = x_i^Tx_j\)
多项式核	\(\kappa(x_i,x_j) = (x_i^Tx_j)^d\)	\(d \ge 1\)为多项式的次数
高斯核	$\kappa(x_i,y_j) = exp(-\frac{
拉普拉斯核	$\kappa(x_i,y_j) = exp(-\frac{
Sigmoid核	\(\kappa(x_i,x_j) = tanh(\beta x_i^Tx_j + \theta)\)	tanh为双曲正切函数，\(\beta>０, \theta< 0\)

Xu_Lin

Do more; Learn more; Be more

机器学习-支持向量机