机器学习-绪论
一、绪论:
(一)机器学习的定义
书本概念:正如我们根据过去的经验来判断明天的天气,吃货们希望从购买经验中挑选一个好瓜,那能不能让计算机帮助人类来实现这个呢?机器学习正是这样的一门学科,人的“经验”对应计算机中的“数据”,让计算机来学习这些经验数据,生成一个算法模型,在面对新的情况中,计算机便能作出有效的判断,这便是机器学习。
(1)Mitchell形式化定义:
假设用P来评估计算机程序在某个任务类T上的性能,若一个程序通过利用经验E在T中任务上获得了性能改善,则我们说关于T和P,该程序对E进行了学习。
从这个定义可以看出机器学习包含四个要素:
1.程序:在这里可以简单地理解为算法或模型
2.任务T: 计算机程序希望实现的任务类。即现实生活中需要解决的问题,例如机器学习在医学影像中的应用:用机器学习根据病人的肺部CT影像预测是否为新冠肺炎患者
3.性能评估P:计算机程序在某任务类别T上的性能。机器学习中的模型和算法有很多种类型,不同的算法在不同问题中表现的性能不同,就算同一个算法,参数不同,性能也会出现差异。
所以,为了更好地预测疾病,我们要设计一个性能评估的方法来选择算法模型和调参。
一般性能度量方法有以下几种:
(1)均方误差
(2)错误率和精度
(3)查准率P、查全率R、F1【PR曲线】
(4)ROC曲线和AUC
4.经验E:这里可以理解为数据集,例如在预测新冠肺炎疾病问题中,肺炎患者肺部CT影像数据为此问题的经验。
机器学习=通过经验E的改进后,机器在任务T上的性能p所度量的性能有所改进=T–>(从E中学习)–>P(提高)
(2)机器学习研究的主要内容:
关于计算机从数据中产生“模型”的算法,即“学习算法”,它是计算机科学的分支。
(3)机器学习的基本术语及概念
数据集(data set):在周志华教授《机器学习》挑选西瓜的例子中,之前挑选过的西瓜样本数据集合;在预测新冠肺炎疾病问题中,所有肺炎患者肺部CT影像数据集合。
定义归纳:由一个或多个具有特定属性的样本(示例)信息和标记信息组合的数据集合。
编号,色泽,根蒂,敲声,纹理,脐部,触感,好瓜
1,青绿,蜷缩,浊响,清晰,凹陷,硬滑,是
2,乌黑,蜷缩,沉闷,清晰,凹陷,硬滑,是
3,乌黑,蜷缩,浊响,清晰,凹陷,硬滑,是
4,青绿,蜷缩,沉闷,清晰,凹陷,硬滑,是
5,浅白,蜷缩,浊响,清晰,凹陷,硬滑,是
6,青绿,稍蜷,浊响,清晰,稍凹,软粘,是
7,乌黑,稍蜷,浊响,稍糊,稍凹,软粘,是
8,乌黑,稍蜷,浊响,清晰,稍凹,硬滑,是
9,乌黑,稍蜷,沉闷,稍糊,稍凹,硬滑,否
10,青绿,硬挺,清脆,清晰,平坦,软粘,否
样本(sample):数据集中的一条记录。
挑选西瓜问题数据集中的一条记录为一个样本:(色泽=青绿;根蒂=蜷缩;敲声=混响);预测新冠肺炎疾病问题中,一位肺炎患者肺部CT影像的记录为一个样本。
属性(attribute)或特征(feature):反映事件或对象在某方面的表现或性质的事项。
特征一般用数值而非文字等其他形态,主要是为了处理和统计分析的方便。
特征的特点是:有信息量,区别性,独立性。背后的思路是通过一个抽象、简化的数学概念来代表复杂的事物。
例如:"色泽"、”根蒂“、”敲声“是西瓜问题中的特征。
属性值(attribute value)或特征值(feature value):属性上的取值。
例如“青绿”为属性值
样本空间/属性空间(sample space)/(attribute space):属性张成的空间。
例如,我们把"色泽"、”根蒂“、”敲声“作为三个坐标轴,他们则张成一个描述西瓜的三维空间。
其中,属性描述的类别个数,称为该样本的维数。
特征向量(feature vector):从n维属性空间中建立每个点都对应一个坐标向量,用来抽象表示事物属性或特征。
特征向量都是为了解决实际问题而专门设计的,比如进行人脸识别的场景使用256维度的向量来代表一个人的面部特征,和进行水果种类识别的场景,使用的特征向量肯定是不一样的。
学习(learning)/ 训练(training):通过执行某个学习算法,从训练数据中学得模型的过程称为“学习”或“训练”。
其中,
- 训练过程中使用的数据称为“训练数据”(training data)
- 每一个样本称为一个“训练样本”(training sample)[特殊]
- 训练样本组成的集合称为“训练集”(training set)。[一般]
- 机器学习出来的模型适用于新样本的能力为:泛化能力(generalization),即从特殊到一般。
假设(hypothesis):学得模型对应了关于数据的某种潜在的规律,因此亦称为“假设”。
其中,这种潜在规律的自身,则称为真相(ground truth),
在机器学习中ground truth表示有监督学习的训练集的分类准确性,用于证明或者推翻某个假设。有监督的机器学习会对训练数据打标记,试想一下如果训练标记错误,那么将会对测试数据的预测产生影响,因此这里将那些正确打标记的数据成为ground truth。
所谓学习过程,就是通过提出假设,验证假设,找出或逼近真相的过程.
标记(label):关于样本结果的信息。
例如西瓜问题中的“好瓜”、“坏瓜”。预测新冠肺炎疾病问题中的“确诊”、“疑似病例”、“普通肺炎”。
其中,所有标记的集合,亦称为“标记空间”(label space)或者“输出空间”。
分类(classification):针对离散值所做预测的学习任务,称为“分类”。例如“好瓜”、“坏瓜”。
回归(regression):针对连续值所做预测的学习任务,称为“回归”。例如西瓜成熟度,密度,含糖率0.697,0.460,0.376。
其中,对只涉及两个类别的“二分类”(binary classification)任务中,通常称其中一个类为“正类”
,另一个类为“反类”(negative class);
比如我们想识别一幅西瓜是不是好瓜。也就是说,训练一个分类器,输入一幅图片,用特征向量x表示,输出是不是好瓜,用y=0或1表示。二类分类是假设每个样本都被设置了一个且仅有一个标签 0 或者 1。
涉及多个类别时,则称为“多分类”(multi-class classification)任务。
比如对一堆水果图片分类, 它们可能是橘子、苹果、梨等.
多类分类是假设每个样本都被设置了一个且仅有一个标签: 一个水果可以是苹果或者梨, 但是同时不可能是两者。
测试(testing):学得模型后,使用其进行预测的过程称为“测试”
其中,被预测的样本称为“测试样本”(testing sample)。
例如在学得f之后,对测试例x1可得到其预测标记y=f(x)。
聚类(clustering):即将训练集中的西瓜分成若干组,每组称为一个“簇”(cluster);
这些自动形成的“簇”可能对应一些潜在的概念划分,例如“浅色瓜”,“深色瓜”,甚至“本地瓜”,“外地瓜”。
这样的学习过程有助于我们了解数据内在的规律,能为更深入地分析数据建立基础.
需要说明的是,在聚类学习中,“浅色瓜”,“深色瓜”这样的概念我们事先是不知道的,而且学习过程中使用的训练样本通常不拥有标记信息。
需注意的是,机器学习的目标是使得学得的模型能很好地适用于“新样本”,而不是仅仅在训练样本上工作得很好;即便对聚类这样的无监督学习任务,我们也希望学得的簇划分能使用在没在训练集出现的样本.学得模型适用于新样本的能力,称为“泛化”(generalizations)能力.
具有强泛化能力的模型能很好地适用于整个样本空间.于是,尽管训练集通常只是样本空间的一个很小的采样,我们仍希望它能很好地反映出样本空间的特性,否则就很难期望在训练集上学得的模型能在整个样本空间上都工作得很好.
通常假设样本空间中全体样本服从于一个未知“分布”(distribution)D,我们获得的每个样本都是独立地从这个分布上采样获得的,也即“独立同分布”.
一般而言,训练样本越多,我们得到关于D的信息越多,这样就越有可能通过学习获得具有强泛化能力的模型.
(4)假设空间
归纳(induction)与演绎(deduction)是科学推理的两大基本手段。
归纳是从特殊到一般的“泛化”(generalization)过程,即从具体的事实归结出一般性规律;
演绎是从一般到特殊的“特化”(specialization)过程,即从基础原理推演出具体情况。
例如,在数学公理系统中,基于一组公理和推理规则推导出与之相恰的定理,这是演绎;
而“从样例中学习”显然是一个归纳的过程,因此亦称“归纳学习”(inductive learning)。
归纳学习有狭义与广义之分,广义的归纳学习大体相当于从样例中学习,而狭义的归纳学习则要求从训练数据中学得概念(concept),因此亦称为“概念学习”或“概念形成”。
概念学习中最基本的布尔概念学习,即对“是”“不是”这样的可表示为0/1布尔值的目标概念的学习。我们做概念学习(归纳学习)的目的是“泛化”,也即通过训练集中数据的学习以获得对尚未出现过的数据进行判断和预测的能力。如果仅仅把训练集中的数据“记住”,今后再见到一样的数据自然可以判断,但对于尚未出现的数据,应该如何处理呢?
我们可以把学习过程看作一个在所有假设(hypothesis)组成的空间中进行搜索的过程,搜索目标是找到与训练集“匹配”(fit)的假设,即能够将训练集中的数据判断正确的假设。假设的表示一旦确定,假设空间及其规模大小也就确定了。
可以有许多策略对这个假设空间进行搜索,例如自顶而下、从一般到特殊,或是自底向上、从特殊到一般,搜索过程中可以不断删除与正例不一致的假设、和(或)与反例一致的假设。最终将会获得与训练集一致(即对所有训练样本能够进行正确判断)的假设,这就是我们学得的结果。
需注意的是,现实问题中我们常常面临很大的假设空间,但学习过程是基于有限样本训练集进行的,因此,可能有多个假设与训练集一致,即存在着一个与训练集一致的“假设集合”,我们称之为“版本空间”(version space)。
(5)归纳偏好
通过学习得到的模型对应了假设空间中的一个假设。但多特征的版本空间往往给我们带来一个麻烦:若出现多个与训练集一致的假设,但与它们对应的模型在面临新样本的时候,却会产生不同的输出。如果我们采用其中一个假设,那么数据将会被判断为真相。而如果采用另外两个假设,则判断的结果将不为真相。那么应该采用哪一个模型(或者说是假设)呢?
若仅有单一的训练样本,则无法断定上述几个假设哪一个“更好”,然而,对于一个具体一点学习算法而言,它必须产生一个模型。这时,学习算法本身的“偏好”就会起到关键的作用。
例如,若我们的算法喜欢“尽可能特殊”的模型,它会选择“样本<->(属性=xx)”
但若我们的算法喜欢“尽可能一般”的模型,并且由于它更“相信”某一属性(特征),则它会选择
“样本<->(属性=*)”。
机器学习算法在学习过程中对某种类型假设但偏好,称为“归纳偏好”(inductive bias),或者简称为“偏好”。
任何一个有效的机器学习算法必有其归纳偏好,否则它将被假设空间中看似在训练集“等效”的假设所迷惑,而无法产生确定的学习结果。可以想象,如果没有偏好,我们的学习算法产生的模型每次在进行预测时随机抽选训集上的等效假设,那么对于某个测试数据,学得模型时而告诉我们它是好的,时而告诉我们它是不好的,这样的学习结果显然是没有意义的。
归纳偏好可看作学习算法自身在一个可能很庞大的假设空间中对假设进行选择的启发式或“价值观”。那么,有没有一般性的原则来引导算法确立“正确的”偏好呢?
这里有以下两种一般性原则作为指导:
“奥卡姆剃刀”(Occam's razor)是一种常用的、自然科学研究中最基本的原则,也即“若有多个假设与观察一致,则选择最简单的那个”。如果采用这个原则,并且假设我们认为“更平滑”意味着“更简单”(例如曲线M更易于描述,而曲线N则复杂得多),则我们将会自然地偏好“平滑”的曲线M。
事实上,归纳偏好对应了学习算法本身所做出的关于“什么样的模型更好”的假设。在具体的现实问题中,这个假设是否成立,即算法的归纳偏好是否与问题本身匹配,大多数时候直接决定了算法能否取得好的性能。
“没有免费的午餐”定理(No Free Lunch Theorem,简称NFL定理),该定力证明了对于所有机器学习问题,算法A更好的概率与算法B更好的概念是一样的。更一般地说,对于所有机器学习问题,任何一种算法(包括瞎猜,乱编)的数学期望效果都是一样的。也即没有一种机器学习算法是适用于所有情况的。
注意,该定理的重要前提是:“对于所有机器学习问题出现的机会(概率)相同,或所有问题同等重要”。但实际情形并不是这样。很多时候,我们只关注自己正在试图解决的问题(例如某个具体应用任务),希望为它找到一个解决方案,至于这个解决方案在别的问题、甚至在相似的问题上是否为好方案,我们并不关心。
NFL定理最重要的寓意,是让我们清楚地认识到,脱离具体问题,空泛地谈论“什么学习算法更好”毫无意义,因为若考虑所有潜在的问题,则所有学习算法都一样好。要讨论算法的相对优劣,必须要针对具体的学习问题;在某些问题上表现好的学习算法,在另一些问题却可能不尽如人意,学习算法自身的归纳偏好与问题是否相配,往往会起到决定性的作用。
这个定理其实揭示了一个哲学思想,“有得必有失”,某一个机器学习算法在某个领域好用,在另外一个领域就有可能不好用,瞎猜在一些情况下不好用,但在某个特定的问题上会很好用。就像能量守恒定理,这里的能量增加,另外一边的能量就会减少。
(二)机器学习的分类和发展历史
(1)机器学习的分类
机器学习的研究分类
R.S.Michalski等人[Michalski ert al.,1983]把机器学习研究划分为“从样例中学习”,“在问题求解和规划中学习”,“通过观察和发现学习”,“从指令中学习等”种类;
E.A.Feigenbaum等人在著名的《人工智能手册》中,则将机器学习划分为“机械学习”,“示教学习”,“类比学习”和“归纳学习”。
其中,机械学习亦称“死记硬背式学习”,即把外界输入的信息全部记录下来,在需要时原封不动地取出来使用,这实际上没有进行真正的学习,仅是在进行信息存储和检索;
“示教学习”和“类别学习”类似于R.S.Michalski所说的“从样例中学习”和“通过观察和发现学习”;
“归纳学习”相当于“从样例中学习”,即从训练样例中归纳初学习结果。
二十世纪八十年代以来,被研究最多、应用最广大事“从样例中学习”(也就是广义的归纳学习),它涵盖了监督学习、无监督学习等。
1. 监督学习和无监督学习
根据训练是否拥有标记信息,学习任务可大致划分为两大类:
“监督学习”(有标记信息)和“无监督学习”(无标记信息),其中分类和回归是监督学习的代表,聚类则是无监督学习的代表。
1.1 监督学习
概念:
通过已有的训练样本去训练得到一个最优模型,再利用这个模型将所有的输入映射为相应的输出,对输出进行简单的判断从而实现预测和分类的目的,也就具有了对未知数据进行预测和分类的能力。简单来说,就像有标准答案的练习题,然后再去考试,相比没有答案的练习题然后去考试准确率更高。监督学习中的数据中是提前做好了分类信息的, 它的训练样本中是同时包含有特征和标签信息的,因此根据这些来得到相应的输出。
有监督算法常见的有:线性回归算法、BP神经网络算法、决策树、支持向量机、KNN等。
数学说明:
监督学习从训练数据集合中训练模型,再对测试据进行预测,训练数据由输入和输出对组成,通常表示为:
测试数据也由相应的输入输出对组成。
有监督学习中,比较典型的问题可以分为:
输入变量与输出变量均为连续的变量的预测问题称为回归问题(Regression),
输出变量为有限个离散变量的预测问题称为分类问题(Classfication),
输入变量与输出变量均为变量序列的预测问题称为标注问题。
应用:
垃圾邮件分类等已知结果的分类问题。
1.2 无监督学习
概念:
训练样本的标记信息未知, 目标是通过对无标记训练样本的学习来揭示数据的内在性质及规律,为进一步的数据分析提供基础,此类学习任务中研究最多、应用最广的是"聚类" (clustering),聚类目的在于把相似的东西聚在一起,主要通过计算样本间和群体间距离得到。深度学习和PCA都属于无监督学习的范畴。
无监督算法常见的有:密度估计(densityestimation)、异常检测(anomaly detection)、层次聚类、EM算法、K-Means算法(K均值算法)、DBSCAN算法 等。
应用:
比较典型的是一些聚合新闻网站(比如说百度新闻、新浪新闻等),利用爬虫爬取新闻后对新闻进行分类的问题,将同样内容或者关键字的新闻聚集在一起。所有有关这个关键字的新闻都会出现,它们被作为一个集合,在这里我们称它为聚合(Clustering)问题。
1.3 二者的对比
有训练样本 vs. 无训练样本: 有监督学习方法必须要有训练集与测试样本。在训练集中找规律,而对测试样本使用这种规律。而无监督学习没有训练集,只有一组数据,在该组数据集内寻找规律。
分类同时定性 vs. 先聚类后定性:有监督学习的方法就是识别事物,识别的结果表现在给待识别数据加上了标签。因此训练样本集必须由带标签的样本组成。而无监督学习方法只有要分析的数据集的本身,预先没有什么标签。如果发现数据集呈现某种聚集性,则可按自然的聚集性分类,但不予以某种预先分类标签对上号为目的。
有 vs. 无 规律性: 无监督学习方法在寻找数据集中的规律性,这种规律性并不一定要达到划分数据集的目的,也就是说不一定要“分类”。这一点是比有监督学习方法的用途要广。譬如分析一堆数据的主分量(PCA),或分析数据集有什么特点都可以归于无监督学习方法的范畴。
分类 vs.聚类:有监督的核心是分类,无监督的核心是聚类(将数据集合分成由类似的对象组成的多个类)。有监督的工作是选择分类器和确定权值,无监督的工作是密度估计(寻找描述数据统计值),也就是无监督算法只要知道如何计算相似度就可以开始工作了。
同维vs.降维:有监督的输入如果是n维,特征即被认定为n维,也即 \(y=f(x_i)\)或\(p(y|x_i),i=n\),常不具有降维的能力。而无监督经常要参与深度学习,做特征提取,或者采用层聚类或者项聚类,以减少数据特征的维度,使 i < n 。
事实上,无监督学习常常被用于数据预处理。一般而言,这意味着以某种平均-保留的方式压缩数据,比如主成分分析(PCA)或奇异值分解(SVD),之后,这些数据可被用于深度神经网络或其它监督式学习算法。
不透明 vs.可解释性: 有监督学习只是告诉你如何去分类,但不会告诉你为什么这样去分类,因此具有不透明性和不可解释性。而无监督学习是根据数据集来聚类分析,再分出类别,因此具有可解释性和透明性,会告诉你如何去分类的,根据什么情况或者什么关键点来分类。
DataVisor无监督独有的扩展性: 根据原有的数据把分类特征已经定好,若增加一组数据,变成了n+1维。那么,如果这是一个非常强的特征,足以将原来的分类或者聚类打散,一切可能需要从头再来,尤其是有监督学习,权重值几乎会全部改变。而DataVisor开发的无监督算法,具有极强的扩展性,无论多加的这一维数据的权重有多高,都不影响原来的结果输出,原来的成果仍然可以保留,只需要对多增加的这一维数据做一次处理即可。
1.4. 如何在两者中选择合适的方法
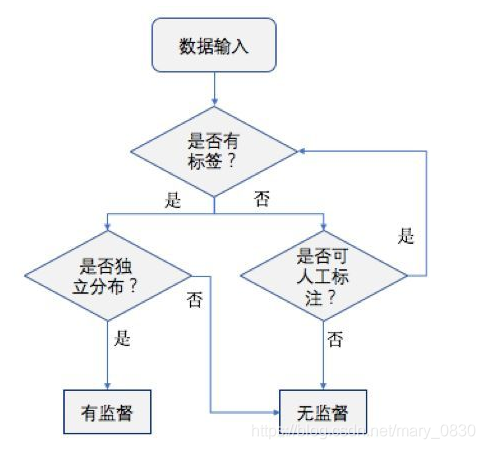
根据上面的图也可以进行分类:!
简单的方法就是从定义入手,有训练样本则考虑采用有监督学习方法;无训练样本,则一定不能用有监督学习方法。但是,现实问题中,即使没有训练样本,我们也能够凭借自己的双眼,从待分类的数据中,人工标注一些样本, 并把它们作为训练样本,这样的话,可以把条件改善,用监督学习方法来做。
(2)机器学习的发展历史
2.2.1 三个时期的时间线
“推理期”(二十世纪五十年代到七十年代初)
(人们认为只要赋予机器逻辑推理能力,机器就具有智能)
随着研究向前发展,人们逐渐认识到,仅具有逻辑推理能力是远远实现不了人工智能的.
“知识期”(二十世纪七十年代中期到二十世纪八十年代)
(大量专家系统问世,在很多应用领域取得了大量成果)
专家系统面临“知识工程瓶颈”,由人来总结知识出来再教给计算机是相当困难的,由此产生让机器自己学习知识的想法.
“学习期”(二十世纪八十年代至今)
先后出现了“统计学习”(statistical learning)以及前一阵十分流行的“深度学习”,而后者只是连接主义学习的第二春。
2.2.2 发展历程
早在1950年,图灵就在关于图灵测试的文章中提到机器学习的可能性.
二十世纪五十年代初已有机器学习的相关研究,例如A.M.Samuel著名的跳棋程序。
五十年代中后期,基于神经网络的“连接主义”(connectionism)学习开始出现,代表性工作有F.Rosenblatt的感知机(Perceptron)、B.Widrow的Adaline等。
在六七十年代,基于逻辑表示的“符号主义”学习技术蓬勃发展,代表性工作有P.Winston的“结构学习系统”、R.S.Michalski等人的“基于逻辑的归纳学习系统”、E.B.Hunt等人多“概念学习系统”等;
以决策理论为基础的学习技术以及强化学习技术等也得到发展,代表性工作有N.J.Nilson的“学习机器”等;二十多年后红极一时的统计学习理论的一些奠基性结果也是在这个时期取得的。
总的来看,二十世纪八十年代是成为一个独立的学科领域,各种机器学习技术百花初绽的时期。
在二十世纪八十年代,“从样例中学习”的一大主流是符号主义学习,
其代表包括决策树和基于逻辑的学习,典型的决策树学习以信息论为基础,以信息熵的最小化为目标,直接模拟了人类对概念进行判定的树形流程。基于逻辑的学习的著名代表是归纳逻辑程序设计(Inductive Logic Programming,简称ILP),可看作机器学习和逻辑程序设计的交叉,它使用了一阶逻辑(即谓词逻辑)来进行知识表示,通过修改和扩充逻辑表达式(例如Prolog表达式)来完成对数据的归纳。符号主义学习占据主流地位与整个人工智能领域的发展历程是分不开的。
在“推理期”,人们基于符号知识表示、通过演绎推理技术取得了很大成就,而在“知识期”,人们基于符号知识表示、通过获取和利用领域知识来建立专家系统取得了大量成果,因此在“学习期”的开始,符号知识表示很自然地受到青睐。
事实上,机器学习在二十世纪八十年代正是被视为“解决知识工程瓶颈问题的关键”,而走上人工智能主舞台的。决策树学习技术由于简单易用,到今天仍是最常用的机器学习技术之一。
ILP具有很强大知识表示能力,可以较容易地表达出复杂数据关系,而且领域知识通常可方便地通过逻辑表达式进行描述,因此ILP不仅可利用领域知识辅助学习,还可以通过学习对领域知识进行精化和增强;然而,成也萧何,败也萧何,由于表示能力太强,直接导致学习过程面领的假设空间太大、复杂度极高,因此问题规模稍大就难以有效进行学习,九十年代中期后这方面的研究相对陷入低潮。
二十世纪九十年代中期之前,“从样例中学习”的另一主流技术是基于神经网络的连接主义学习。连接注意学习在二十世纪五十年代取得了大发展,但早期的很多人工智能研究者对符号表示又特别偏爱,所以当时连接主义的研究未被纳入主流人工智能研究范畴,尤其是连接注意自身也遇到了很大的障碍。
[正如图灵奖得主M.Minsky和S.Papert在1969年指出,(当时的)神经网络只能处理线性分类,甚至对“异或”这样简单的问题都处理不了]
[1983年J.J.Hopfield利用神经网络求解“流动推销员”这个著名的NP难题取得了重大进展,使得连接注意重新受到人们关注]
[1986年,D.E.Rumelhart等人重新发明了著名的BP算法,产生了深远影响]
与符号主义学习能产生明确的概念表示不同,连接主义学习产生的是“黑箱”模型,因此从知识获取的角度来看,连接主义学习技术有明显弱点;然而由于有BP这样有效的算法,使得它可以在很多现实问题上发挥作用。事实上,BP一直说被应用得最广泛的机器学习算法之一。
连接主义学习等最大局限是其“试错性”;简单来说,其学习过程涉及大量参数,而参数的设置缺乏理论指导,主要靠手工“调参”,夸张一点说,参数调节上失之毫厘,学习结果可能就谬以千里。
二十世纪九十年代中期,“统计学习”(statistical learning)闪亮登场并迅速占据主流舞台,代表性技术活是支持向量机(Support Vector Machine,简称SVM)以及更一般的“核方法”(kernel method)。这方面的研究早在二十世纪六七十年代就已开始,统计学习理论[Vapnik,1998] 在那个时期也打下来基础,例如V.N.Vapnik在1963年提出来“支持向量概念”,他和A.J.Chervonenkis在1968年提出的VC维,在1974年提出来结构风险最小化原则等。但直到九十年代中期统计学习方法才开始称为及其学习等主流,一方面是由于有效的支持向量机算法在九十年代初才被提出,其优越性能到九十年代中期在文本分类应用中才得以显现;另一方面,正是在连接注意学习技术等局限性凸现之后,人们才把目光转向了以统计学习理论为直接支撑的统计学习技术。
事实上,统计学习与连接主义学习有密切的联系,在支持向量机被普遍接受后,核技巧(kernel trick)被人们用到了机器学习的几乎每一个角落,核方法也逐渐成为机器学习等基本内容之一。
有趣的事,二十一世纪初,连接主义学习又卷土重来,掀起了以“深度学习”为名的热潮。
所谓“深度学习”,狭义地说就是“很多层”的神经网络。
在若干测试和竞赛熵,尤其是涉及语音、图像等复杂对象的应用中,深度学习技术取得了优越性能。
以往机器学习技术在应用中药取得好性能,对使用者的要求较高;而深度学习技术涉及的模型复杂度非常高,以至于只要下功夫“调参”,把参数调节好,性能往往就好。因此深度学习虽然缺乏严格的理论基础,但它显著降低了机器学习应用者的门槛,为机器学习技术走向工程实践带来了便利。
那么,它为什么此时才热起来呢?有两个基本原因:数据大了、计算能力强了。
深度学习模型拥有大量参数,若数据样本少,则很容易“过拟合”;
如此复杂的模型、如此大的数据样本,若缺乏强力计算设备,根本无法求解。
恰好由于人类进入“大数据时代”,数据储量与计算设备都有了大发展,这才使得连接注意学习技术焕发又一春。有趣的事,神经网络在二十世纪八十年代中期走红,与当时Inter x86系列微处理器与内存条技术的广泛应用所造成的计算能力、数据访存效率比七十年代有显著提高不无关联。
深度学习此时的状况,与彼时的神经网络何其相似。
2.2.3 流派
2.2.3.1 符号主义
符号主义又称逻辑主义、心理学派或计算机学派。符号主义认为,人工智能源于数学逻辑,人的认知基源是符号,认知过程即符号操作过程,通过分析人类认知系统所具备的功能和机能,然后通过计算机来模拟这些功能,从而实现人工智能。符号主义的发展大概经历了几个阶段:
推理期(20世纪50年代–20世纪70年代),
知识期(20世纪70年代—-)。
“推理期”人们基于符号知识表示、通过演绎推理技术取得了很大的成就;“知识期”人们基于符号表示、通过获取和利用领域知识来建立专家系统取得了大量的成果。
符号主义认为人工智能源于数理逻辑。数理逻辑从19世纪末起得以迅速发展,到20世纪30年代开始用于描述智能行为。计算机出现后,又在计算机上实现了逻辑演绎系统。其有代表性的成果为启发式程序LT逻辑理论家,它证明了38条数学定理,表明了可以应用计算机研究人的思维过程,模拟人类智能活动。正是这些符号主义者,早在1956年首先采用“人工智能”这个术语。后来又发展了启发式算法>专家系统>知识工程理论与技术,并在20世纪80年代取得很大发展。符号主义曾长期一枝独秀,为人工智能的发展作出重要贡献,尤其是专家系统的成功开发与应用,为人工智能走向工程应用和实现理论联系实际具有特别重要的意义。在人工智能的其他学派出现之后,符号主义仍然是人工智能的主流派别。这个学派的代表人物有纽厄尔(Newell)、西蒙(Simon)和尼尔逊(Nilsson)等。
2.2.3.2 连接主义
连接主义又称仿生学派或生理学派。连接主义认为,人工智能源于仿生学,特别是对人脑模型的研究,人的思维基元是神经元,而不是符号处理过程。20世纪60~70年代,连接主义,尤其是对以感知机(perceptron)为代表的脑模型的研究出现过热潮,由于受到当时的理论模型、生物原型和技术条件的限制,脑模型研究在20世纪70年代后期至80年代初期落入低潮。直到Hopfield教授在1982年和1984年发表两篇重要论文,提出用硬件模拟神经网络以后,连接主义才又重新抬头。1986年,鲁梅尔哈特(Rumelhart)等人提出多层网络中的反向传播算法(BP)算法。进入21世纪后,连接主义卷土重来,提出了“深度学习”的概念。此后,连接主义势头大振,从模型到算法,从理论分析到工程实现,为神经网络计算机走向市场打下基础。现在,对人工神经网络(ANN)的研究热情仍然较高,但研究成果没有像预想的那样好。
2.2.3.3 行为主义
认为人工智能源于控制论。控制论思想早在20世纪40-50年代就成为时代思潮的重要部分,影响了早期的人工智能工作者。维纳(Wiener)和麦克洛克(McCulloch)等人提出的控制论和自组织系统以及钱学森等人提出的工程控制论和生物控制论,影响了许多领域。控制论把神经系统的工作原理与信息理论、控制理论、逻辑以及计算机联系起来。早期的研究工作重点是模拟人在控制过程中的智能行为和作用,如对自寻优、自适应、自镇定、自组织和自学习等控制论系统的研究,并进行“控制论动物”的研制。到20世纪60~70年代,上述这些控制论系统的研究取得一定进展,播下智能控制和智能机器人的种子,并在20世纪80年代诞生了智能控制和智能机器人系统。行为主义是20世纪末才以人工智能新学派的面孔出现的,引起许多人的兴趣。这一学派的代表作者首推布鲁克斯(Brooks)的六足行走机器人,它被看作是新一代的“控制论动物”,是一个基于感知-动作模式模拟昆虫行为的控制系统。
(三)机器学习的应用领域
在今天,计算机科学的诸多分支学科领域中,无论是多媒体、图形学,还是网络通信、软件工程,乃至体系结构、芯片涉及,都能找到机器学习技术等身影,尤其是在计算机视觉、自然语言处理等“计算机应用技术”领域,机器学习已经成为最重要的技术进步源泉之一。
3.1 机器学习的应用范围
机器学习与模式识别、统计学习、数据挖掘、计算机视觉、语音识别、自然语言处理等领域有着非常深的联系。
-
模式识别=机器学习
两者的主要差别在于前者是从工业界发展起来的概念,后者则主要源自计算机学科。
它们中的活动能够被视为同一个领域的两个方面。 -
数据挖掘=机器学习+数据库
数据挖掘是一个思考方式,告诉我们应该尝试从数据中挖掘出知识,但不是每一个数据都能挖掘出金子的。
一个系统绝对不会由于上了一个数据挖掘模块就变得无所不能。大部分数据挖掘中的算法是机器学习的算法在数据库中的优化。
数据挖掘是从海量数据中发掘知识,这就必然涉及对“海量数据”的管理和分析。大体来说,数据库领域的研究为数据挖掘提供数据管理技术,而机器学和统计学习的研究为数据挖掘提供数据分析技术。
- 模式识别=机器学习
两者的主要差别在于前者是从工业界发展起来的概念,后者则主要源自计算机学科。
它们中的活动能够被视为同一个领域的两个方面。 - 统计学习约等于机器学习
统计学习是与机器学习高度重叠的学科,由于机器学习中的大多数来自统计学,甚至可以认为,统计学的发展促进机器学习的发展。 - 计算机视觉=图像处理+机器学习
图像处理技术用于将图像处理为适合进入机器学习模型中的输入,机器学习则负责从图像中识别出相关的模式。计算机视觉相关的应用非常多,例如百度识图、手写字符识别、车牌识别等应用。 - 语音识别=语音处理+机器学习
语音识别就是音频处理技术与机器学习的结合。语音识别技术一般不会单独使用,通常会结合自然语言处理的相关技术,有关的应用有苹果的语音助手Siri等。 - 自然语言处理=文本处理+机器学习
自然语言处理技术主要是让机器理解人类的语言的一门领域。
参考材料:
[1]周志华教授「机器学习」绪论
[2]CSDN博主「Liaojiajia-2020」原文链接:https://blog.csdn.net/mary_0830/article/details/96323281
[3]CSDN博主「poppy_zlw」原文链接:https://blog.csdn.net/zrj000za/article/details/72967128


 浙公网安备 33010602011771号
浙公网安备 33010602011771号