[机器学习笔记]幂次学院西瓜书集训营-概率论基础
概率论基础
1.为何使用概率
概率论是用于表示不确定性声明的数学框架。它不仅提供了量化不确定性的方法,也提供了用于导出新的不确定性声明(statement)的公理。
概率论主要有两种用途。
首先,概率法则告诉我们AI系统如何推理,据此我们设计一些算法来计算或者估算由概率论导出的表达式。其次,我们可以用概率和统计从理论上分析我们提出的AI系统的行为。
概率论使我们能够提出不确定的声明以及在不确定性存在的情况下进行推理,而信息论使我们能够量化概率分布中的不确定性总量。
计算机科学的许多分支处理的实体大部分都是完全确定且必然的。程序员通常可以安全地假定CPU将完美地执行每条机器指令。虽然硬件错误确实会发生,但它们足够罕见,以至于大部分软件应用在设计时并不需要考虑这些因素的影响。
机器学习对于概率论的大量使用是很令人吃惊的。
这是因为机器学习通常必须处理不确定量,有时也可能需要处理随机(非确定性的)量。
不确定性和随机性可能来自多个方面。至少从20世纪80年代开始,研究人员就对使用概率论来量化不确定性提出了令人信服的论据。
不确定性有三种可能的来源:
1.被建模系统内在的随机性。
例如,大多数量子力学的解释,都将亚原子例子的动力学描述为概率的。
我们还可以创建一些我们假设具有随机动态的理论情景。
例如,一个假想的纸牌游戏,在这个游戏中我们假设纸牌被真正混洗成了随机顺序。
2.不完全预测。
即使是确定的系统,当我们不能观测到所有驱动系统行为的变量时,该系统也会呈现随机性。例如,在Monty Hall问题中,一个游戏节目的参与者被要求在三个门之间选择,并且会赢得放置在选中门后的奖品。其中两扇门通向山羊,第三扇门通向一辆汽车。选手的每个选择所导致的结果是确定的,但是站在选手的角度,结果是不确定的。(注:即为观测角度的问题)
3.不完全建模。
当我们使用一些必须舍弃某些观测信息的模型时,舍弃的信息会导致模型的预测出现不确定性。例如,假设我们制作了一个机器人,它可以准确地观察周围每一个对象的位置。在对这些对象将来的位置进行预测时,如果机器人采用的是离散化的空间,那么离散化的方法将使得机器人无法确定对象们的精确位置:因为每个对象都可能处于它被观测到的离散单元的任何一个角落。
在很多情况下,使用一些简单而不确定的规则要比复杂而确定的规则更为实用,即使真正的规则是确定的,并且我们建模的系统可以足够精确地容纳复杂的规则。
例如,“多数鸟儿都会飞”这个简单的规则描述起来很简单,并且使用广泛,而正式的规则——“除了那些还没学会飞翔的幼鸟,因为生病或是受伤而失去了飞翔能力的鸟,包括食火鸟(cassowary)、鸵鸟(ostrich)、几维(kiwi)等不会飞的鸟类……以外,鸟儿会飞”,很难应用、维护和沟通,即使经过这么多的努力,这个规则还是很脆弱而且容易失败。
概率论最初的发展是为了分析事件发生的概率。
我们可以很容易地看出概率论,对于像在扑克牌游戏中抽出一手特定的牌这种事件的研究中,是如何使用的。这类事件往往是可以重复的。当我们说一个结果发生的概率为p,这意味着如果我们反复实验(例如,抽一手牌)无限次,有p的比例可能会导致这样的结果。
这种推理似乎并不立即适用于那些不可重复的命题。
如果一个医生诊断了病人,并说该病人患流感的几率为40%,这意味着非常不同的事情——我们既不能让医生有无穷多的副本,也没有任何理由去相信病人的不同副本在具有不同的潜在条件下表现出相同的症状。在医生诊断病人的例子中,我们可以用概率来表示一种信任度(置信度)(degree of belief),其中1表示非常肯定病人患有流感,而0表示非常肯定病人没有流感。
前面那种概率,直接与事件发生的概率相联系,被称为频率派概率(frequentist probability);而后者,设计确定性水平,被称为贝叶斯概率(Bayesian probability)。
概率可以被看作是用于处理不确定性的逻辑扩展。逻辑提供了一套形式化的规则,可以子啊给定某些命题是真或假的假设下,判断另外一些命题是真的还是假的。
概率论提供了一套形式化的规则,可以在给定一些命题的似然后,计算其他命题为真的似然。
2.随机变量
随机变量(random variable)是可以随机地取不同值的变量。我们通常用无格式字体(plain typeface)中的小写字母来表示随机变量本身,而用手写体中的小写字母来表示随机变量能够取到的值。例如x1和x2都是随机变量x可能的取值。
对于向量值变量,我们会将随机变量写成x,它的一个可能取值为x。
就其本身而言,一个随机变量只是对可能的状态的描述;它必须伴随着一个概率分布来指定每个状态的可能性。
随机变量可以是离散的或者连续的。离散随机变量拥有有限或者可数无限多的状态。
注意这些状态不一定非要是整数;它们也可能只是一些被命名的状态而没有数值。连续随机变量伴随着实数值。
3.概率分布

离散型变量和概率质量函数





连续型变量和概率密度函数


4.边缘概率与条件概率
边缘概率


例1


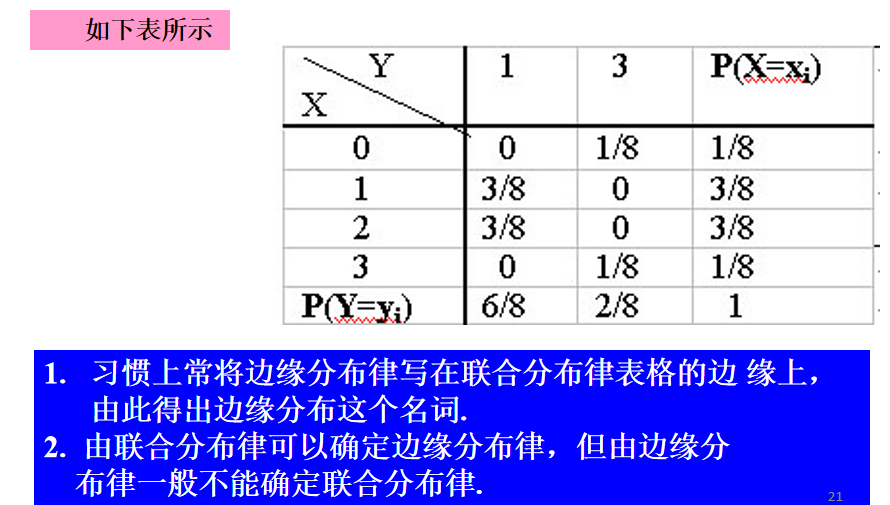
条件概率

5.独立性
独立性和条件独立性


6.期望,方差
随机变量的数字特征
分布函数能完整地描述随机变量的统计特性, 但实际应用中, 有时并不需要知道分布函数而只需知道随机变量的某些特征。
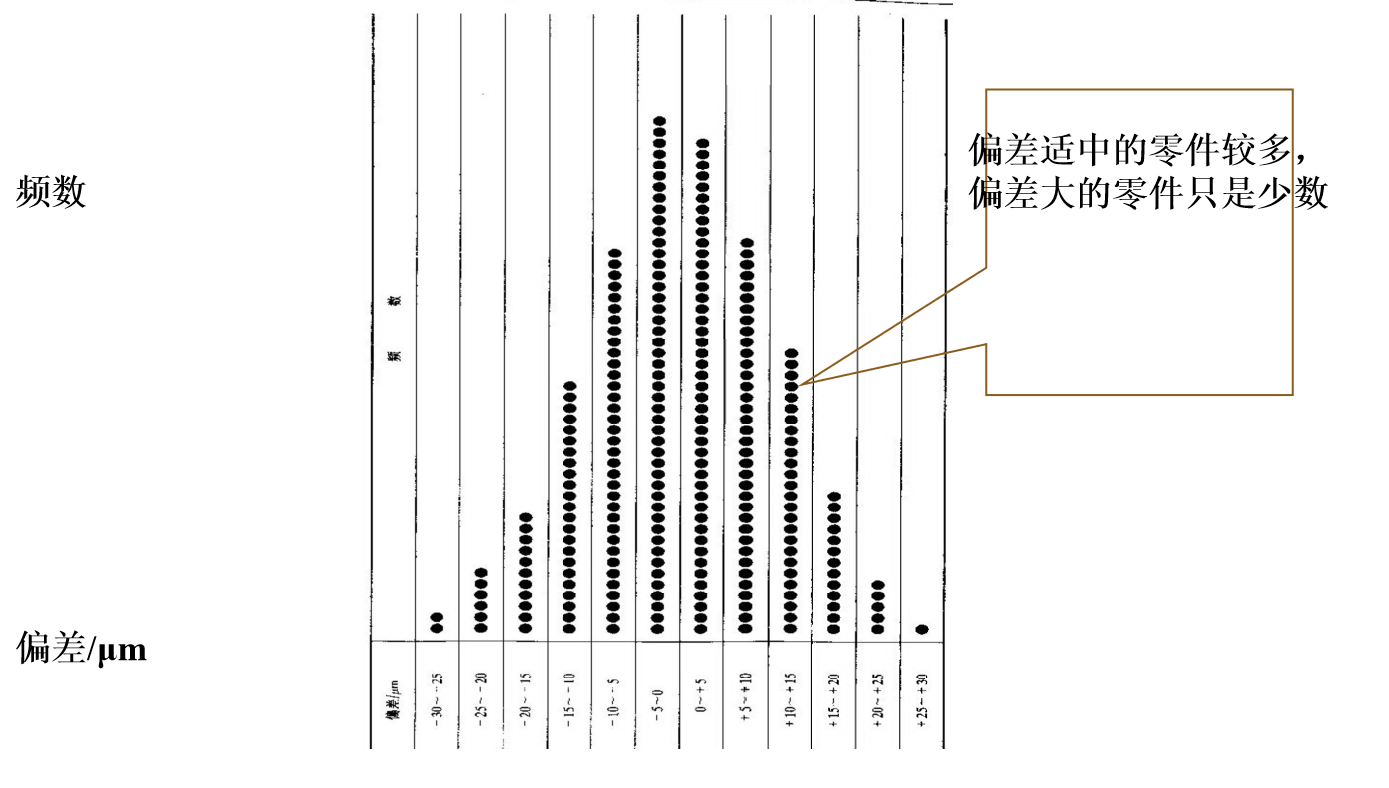
例如:判断棉花质量时, 既看纤维的平均长度,又要看 纤维长度与平均长度的偏离程度,平均长度越长,偏离程度越小, 质量就越好;考察一射手的水平, 既要看他的平均环数是否高, 还要看他弹着点的范围是否小, 即数据的波动是否小.由上面例子看到,与随机变量有关的某些数值,虽不能完整地描述随机变量,但能清晰地描述随机变量在某些方面的重要特征, 这些数字特征在理论和实践上都具有重要意义。
为了引入随机变量的数学期望的概念,我们先看一个例子。假设有1000根钢筋,其中200根长0.98米;300根长0.99米;400根长1米;100根长1.01米,求其平均长度。
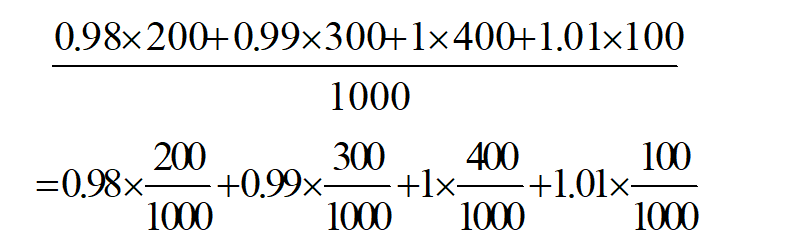
而2/10;3/10;4/10;1/10分别是从1000根钢筋中,任意抽取一根它的尺寸分别为0.98;0.99;1;1.01的概率。由此可以引出下面的随机变量的数学期望的定义。
数学期望的定义


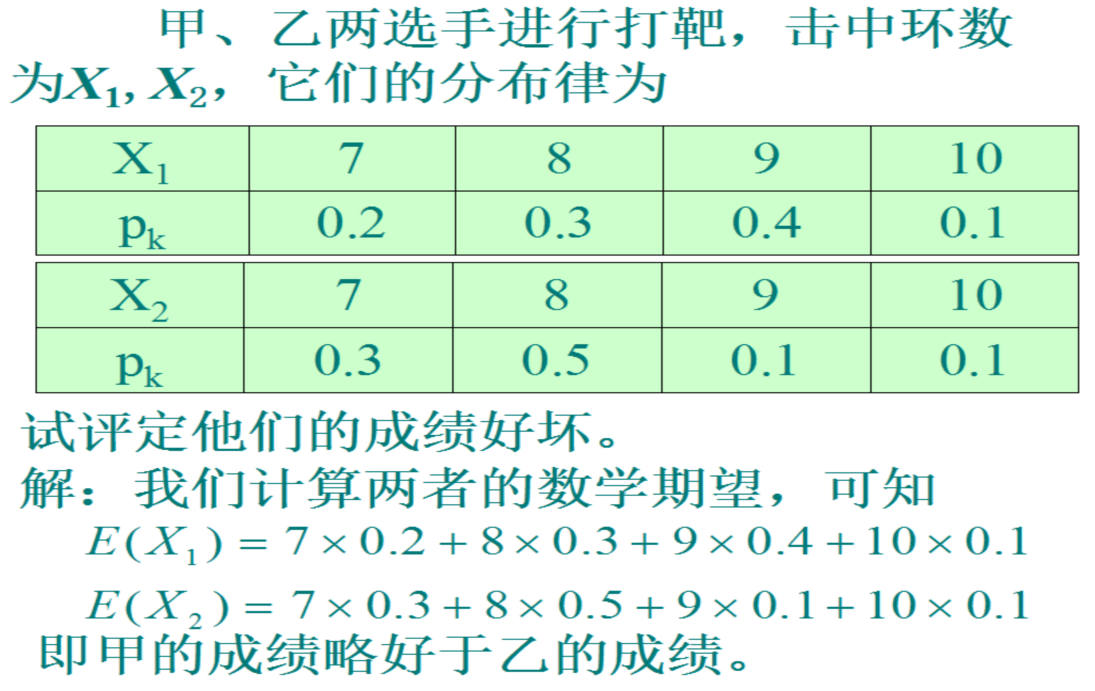

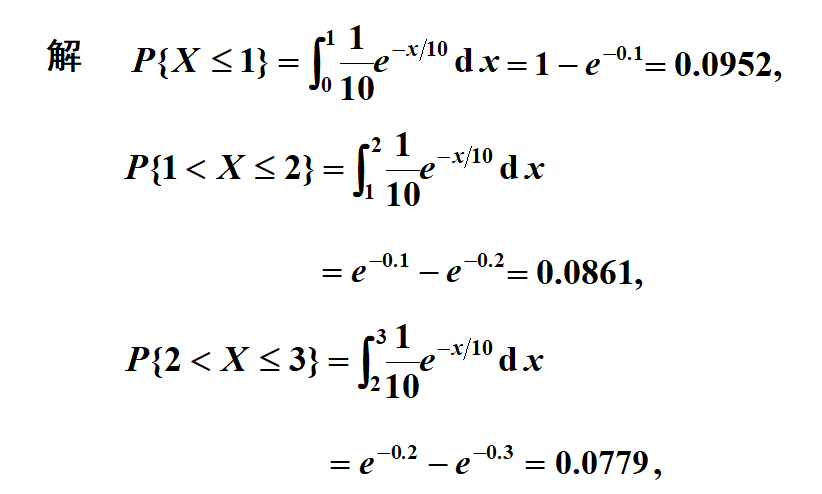


方差



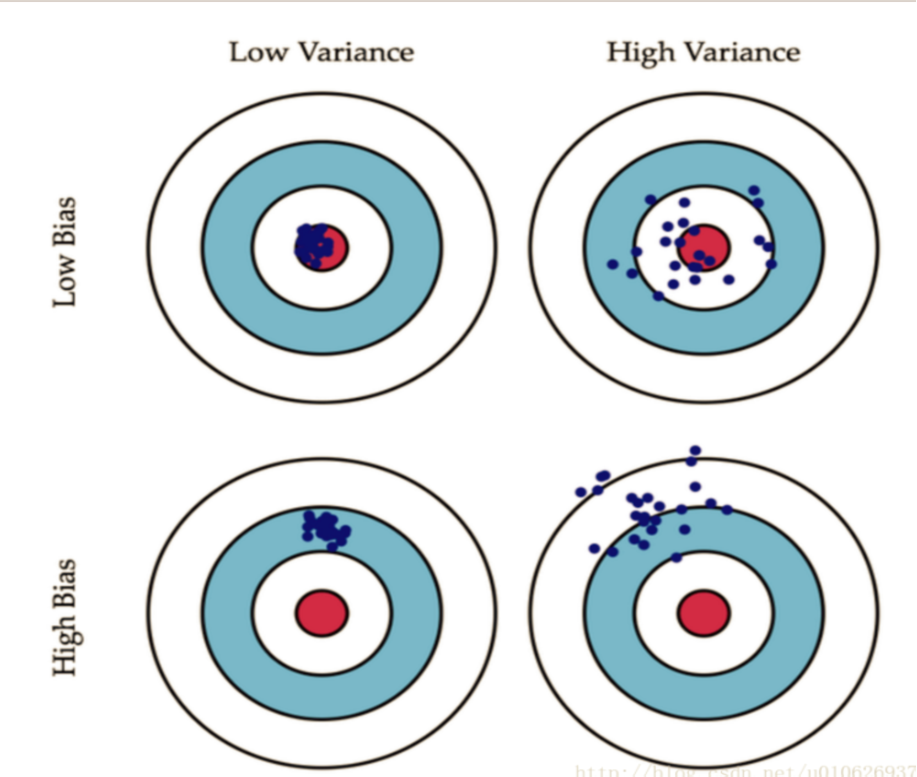
常见的概率分布
离散随机变量的分布
Bernoulli分布

二项分布

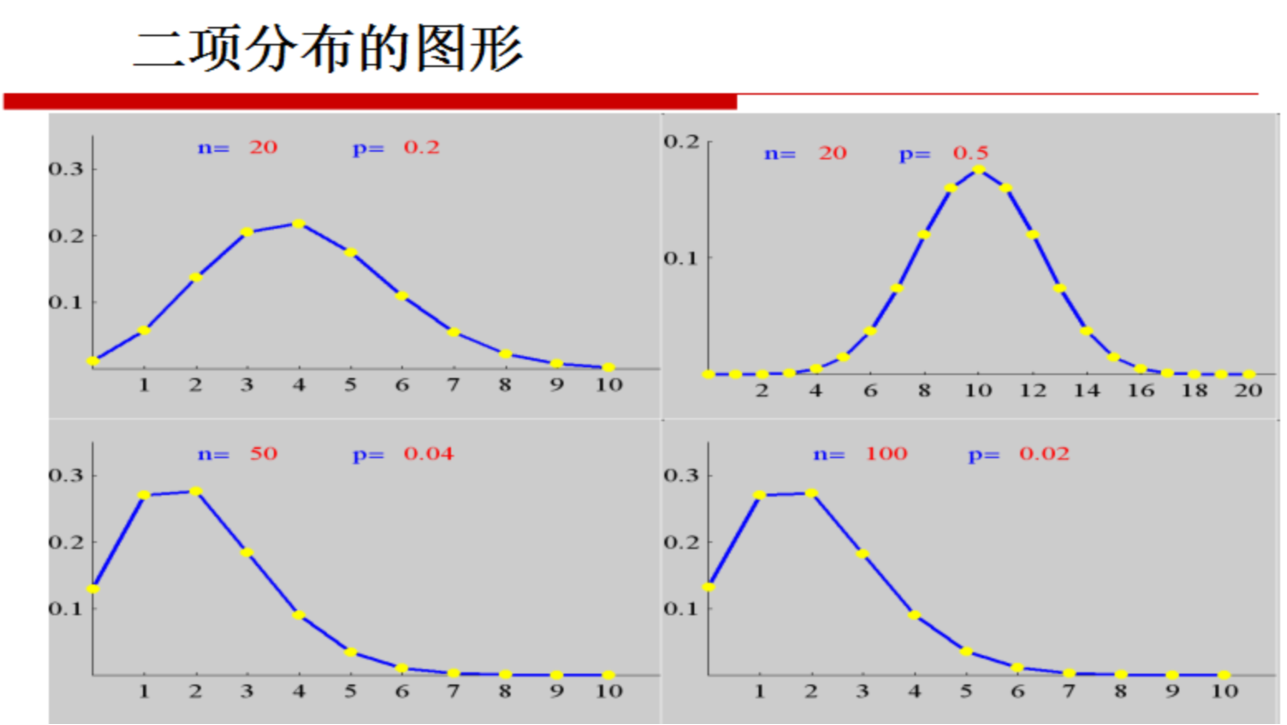

泊松分布

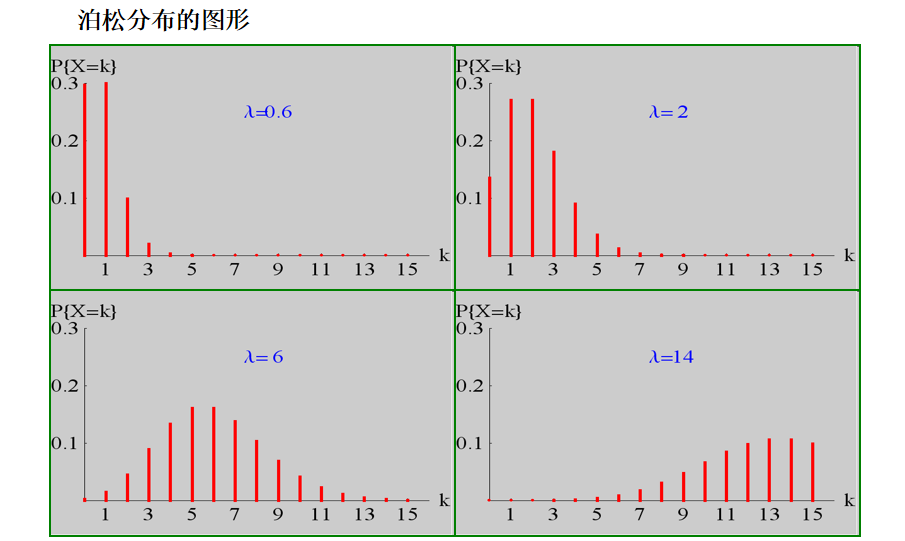




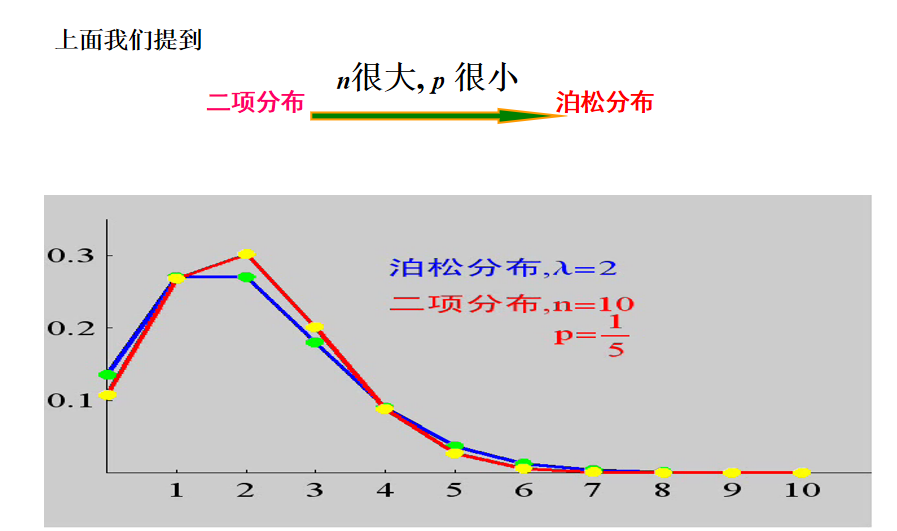
几何分布

常见的分布律
(0 – 1)分布
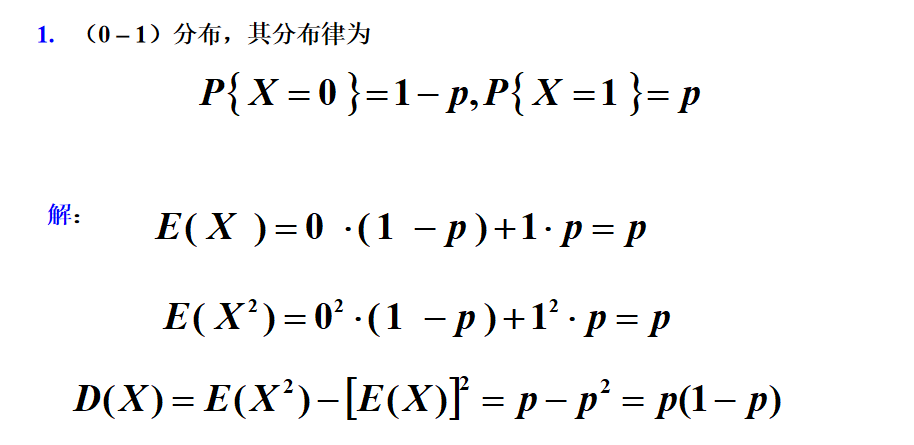
二项分布

泊松分布

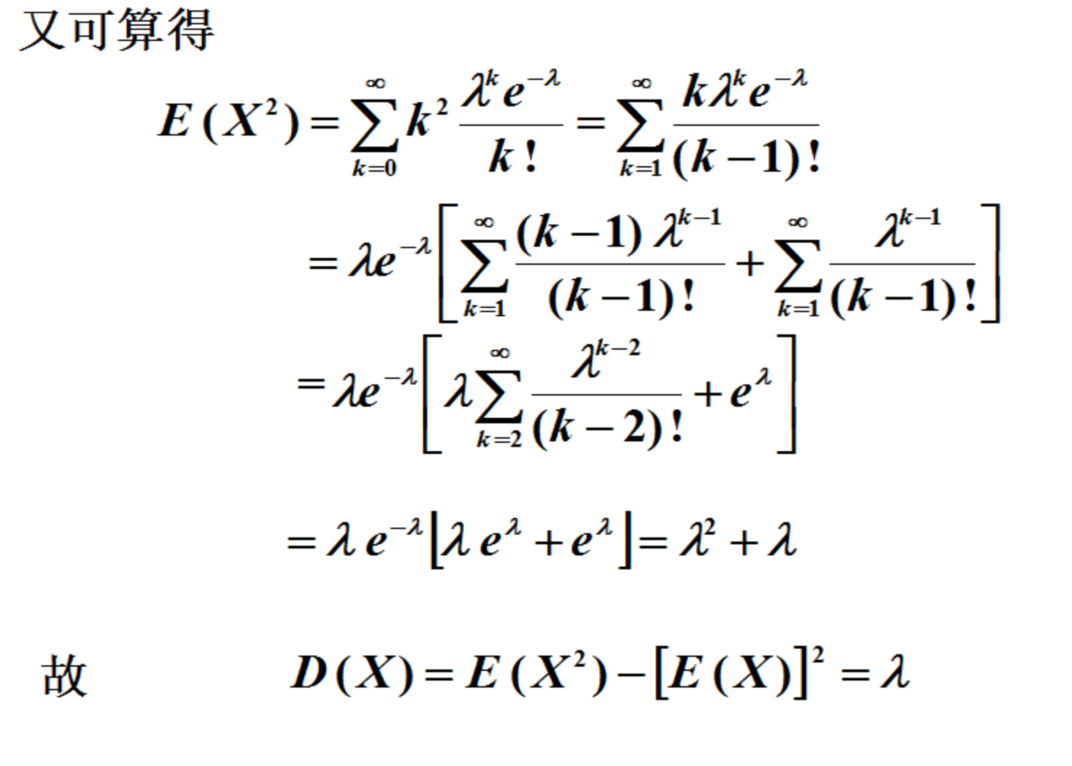
常用离散分布的数学期望

常用离散分布的方差



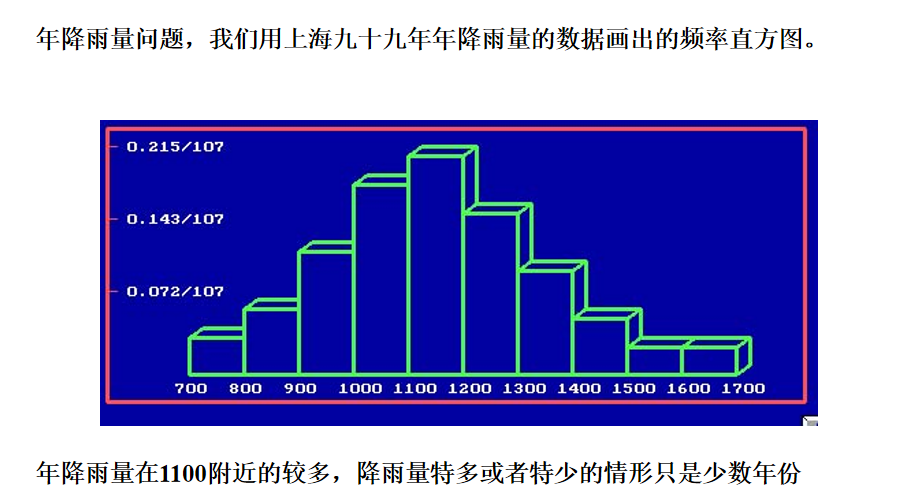
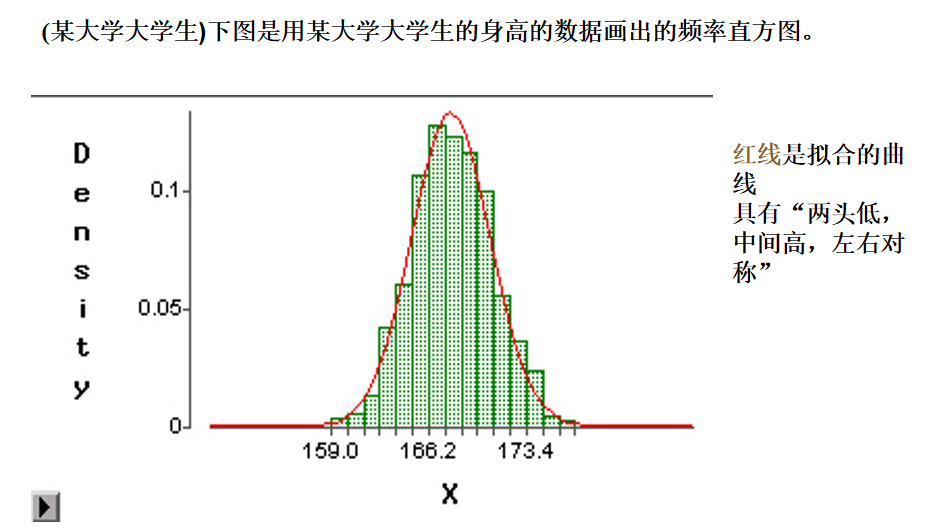
正态分布

正态分布的定义


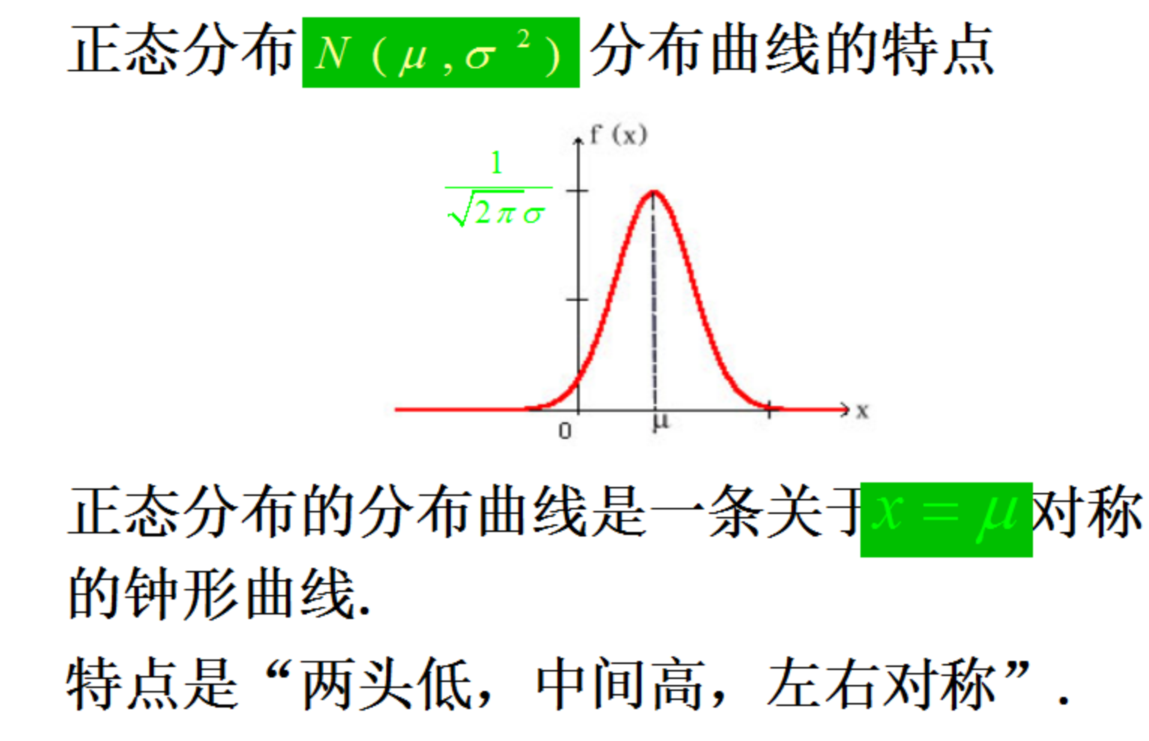
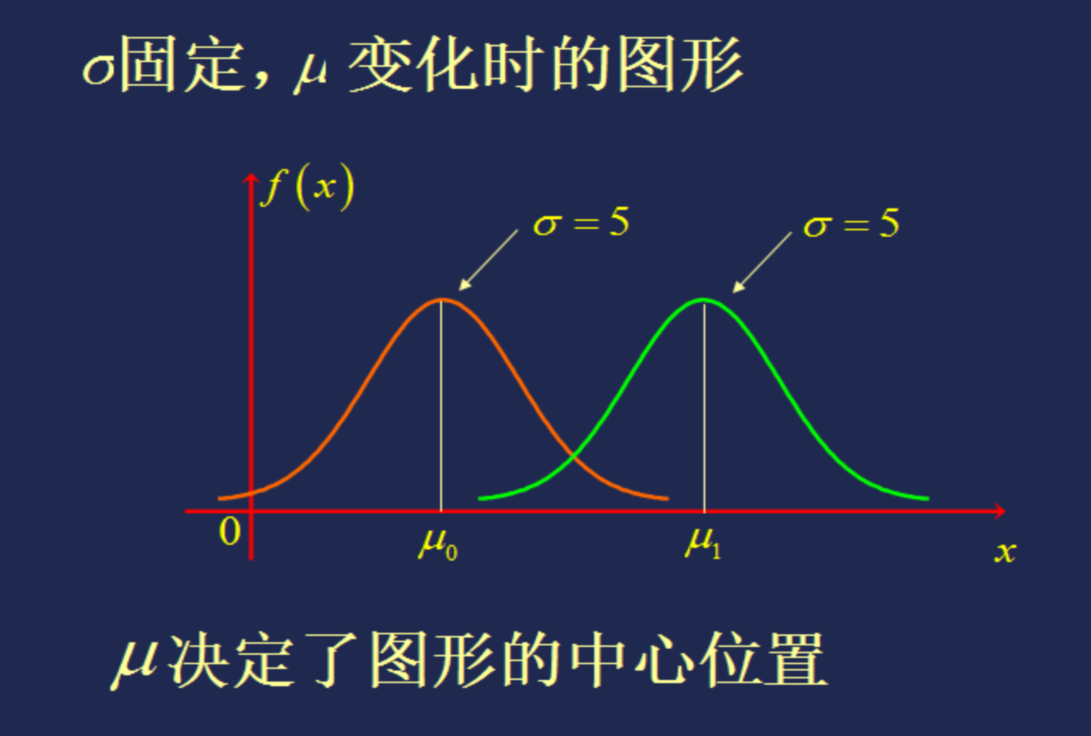
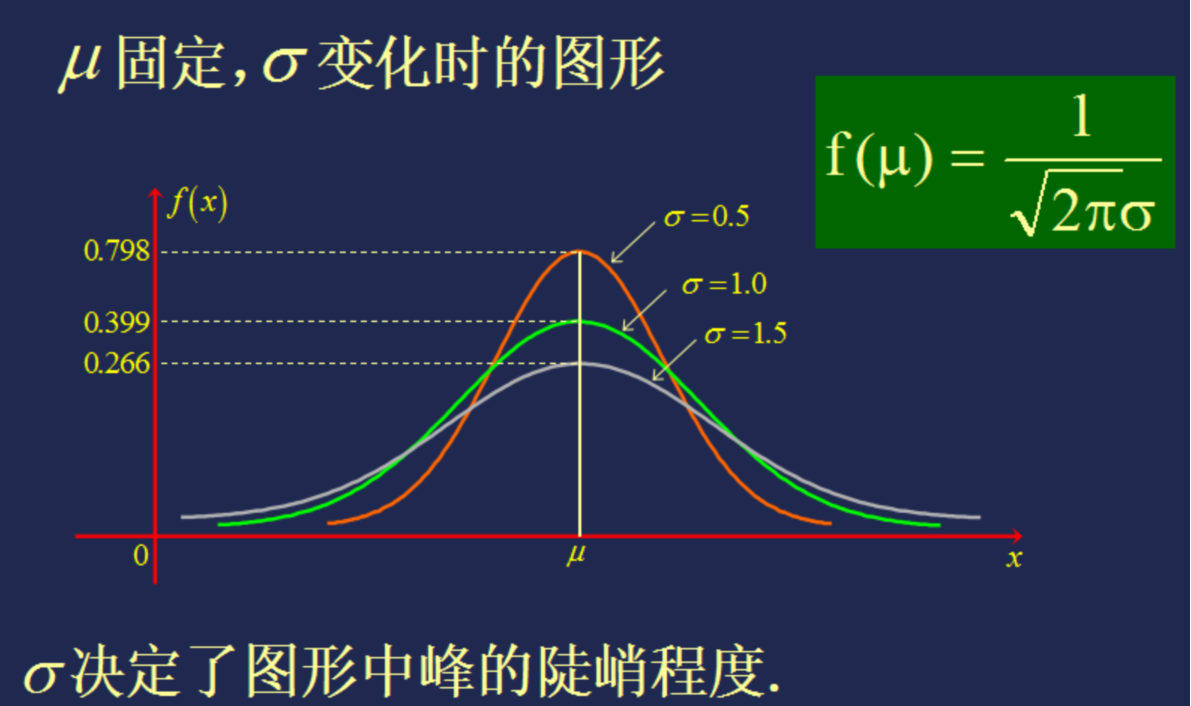
标准正态分布
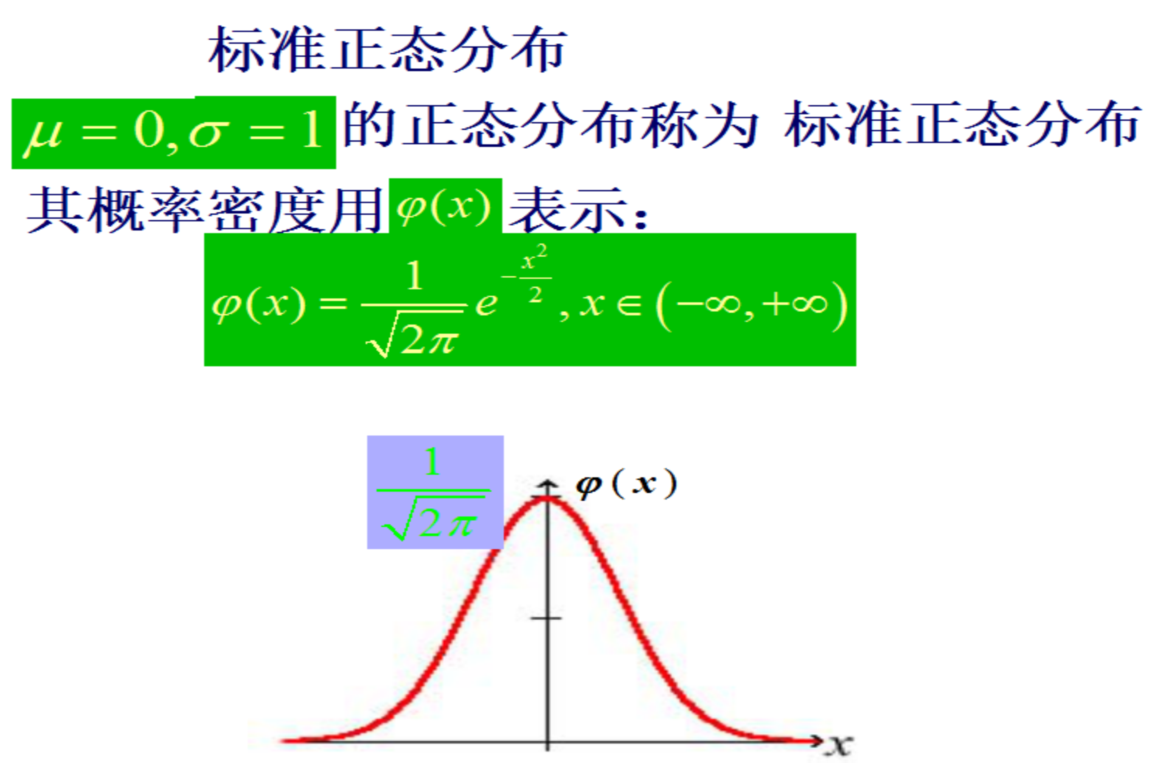


作业1
作业:python实现
- 使用python的scipy包的stats模块生成正太分布数据,并画图
- 写一个二项分布的例子,并画图
条件概率及相关公式

引例


一、条件概率


二、乘法公式

例1

作业1

三、全概率公式


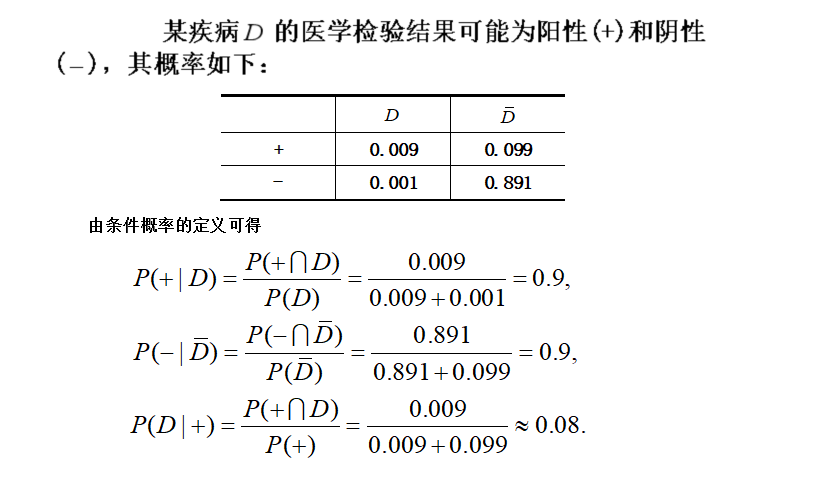
例2

例3

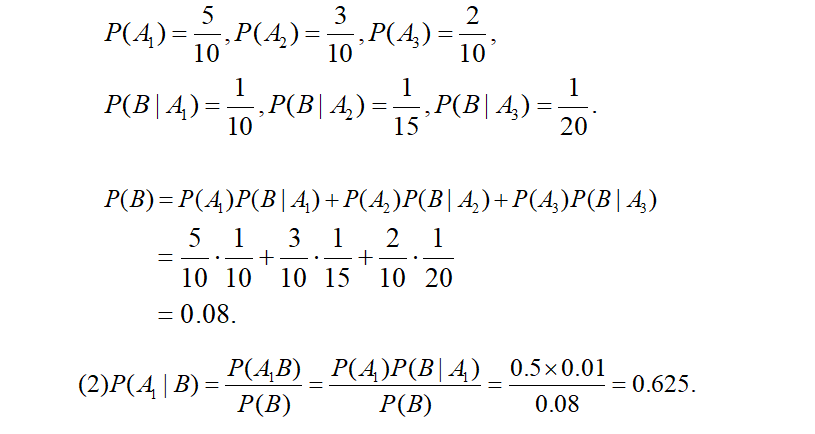
四、贝叶斯公式


例4

例5

例6

作业

作业讲解
- 使用python的scipy包的stats模块生成正态分布数据,并画图
- 写一个二项分布的例子,并画图


 浙公网安备 33010602011771号
浙公网安备 33010602011771号