[机器学习笔记]幂次学院西瓜书集训营-线性代数

目录

• 课程大纲
  • 第一章
    • 初步认识
      • 标量(scalar)
      • 向量(vector)
      • 矩阵(matrix)
      • 张量(tensor)
    • 矩阵和向量运算
      • 转置
      • 矩阵加法
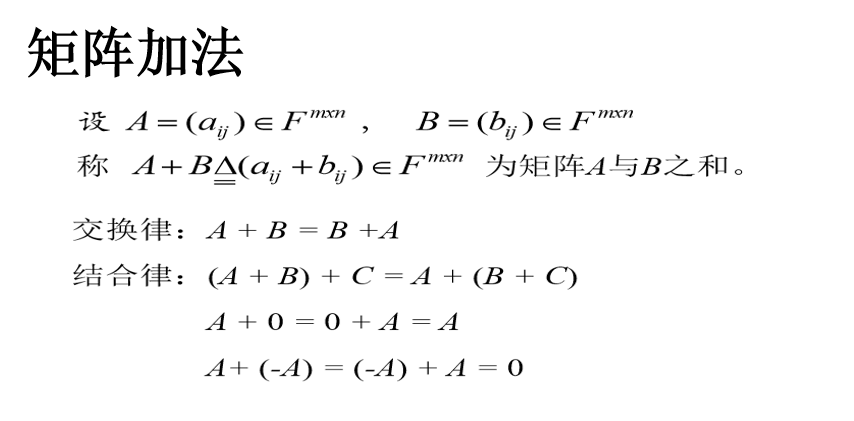
      • 矩阵减法
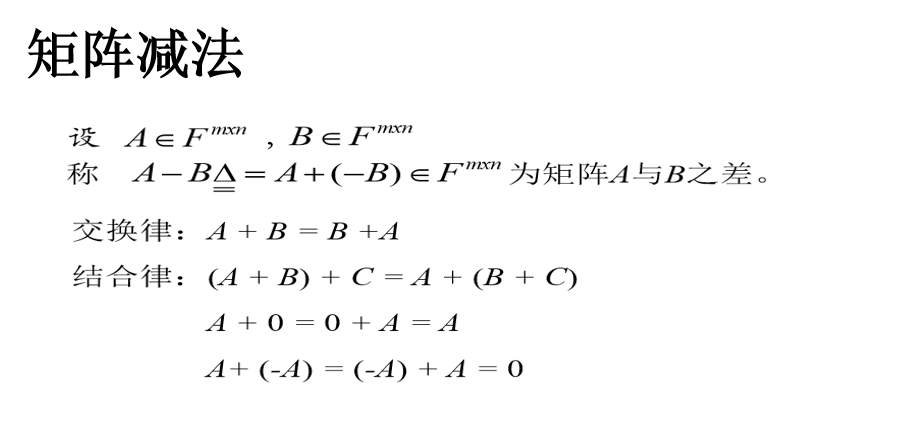
      • 数乘矩阵
      • 矩阵乘法
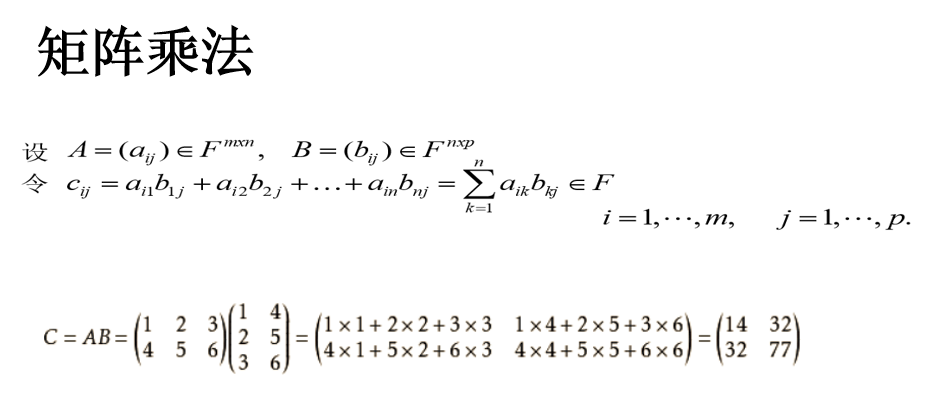
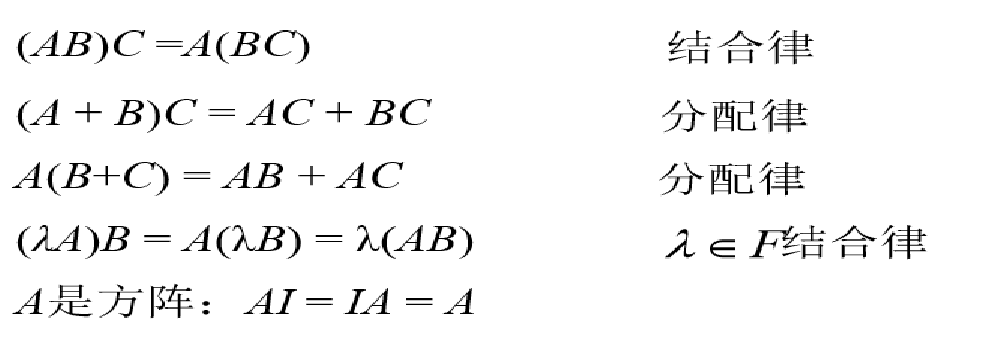
      • 积乘（元素对应乘积）
      • 点积
      • 线性方程组
    • 两种特殊矩阵
      • 逆矩阵
      • 单位矩阵
  • 第二章
    • 线性相关
      • 一、向量的线性组合、线性表示
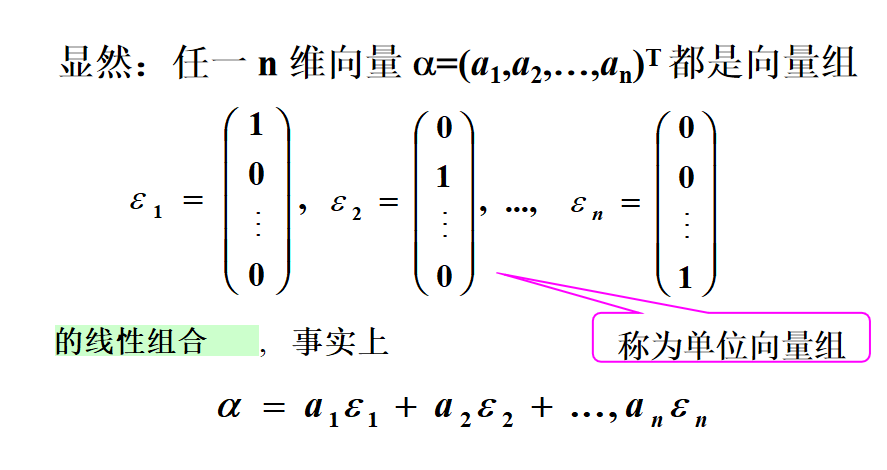
      • 二、向量组的线性相关与线性无关
        • 例1
        • 例2
    • 线性空间及其子空间
      • 一、线性空间定义
      • 二、线性空间例子
        • 例1
        • 例2
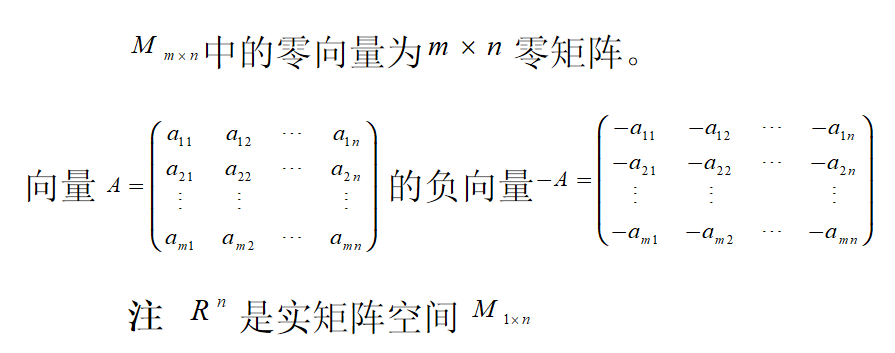
      • 三、线性空间的子空间
        • 判断下列集合是否为线性空间
        • 继续理解线性空间
        • 线性子空间
      • 作业1
  • 第三章
    • 范数
    • 特殊类型的矩阵与向量
      • 对角矩阵
      • 对称矩阵
      • 正交矩阵
      • 单位向量
      • 作业2
  • 第四章 矩阵分解
    • 一、特征分解
    • 二、奇异值分解
      • 关于SVD一个代码例子
    • 作业3

课程大纲

第一章

初步认识

标量(scalar)

向量(vector)

矩阵(matrix)

张量(tensor)

矩阵和向量运算

转置

矩阵加法

矩阵减法

数乘矩阵

矩阵乘法

积乘（元素对应乘积）

点积

线性方程组

两种特殊矩阵

逆矩阵

单位矩阵

第二章

线性相关

一、向量的线性组合、线性表示

二、向量组的线性相关与线性无关

例1

例2

线性空间及其子空间

一、线性空间定义

二、线性空间例子

例1

例2

三、线性空间的子空间

判断下列集合是否为线性空间

继续理解线性空间

线性子空间

作业1

用python表示向量，矩阵和张量。下面说的都是基于python的编程。
求向量，矩阵和张量的shape
实现向量的点积
实现矩阵的加法和乘法、元素对应乘积

第三章

范数

特殊类型的矩阵与向量

对角矩阵

对称矩阵

正交矩阵

单位向量

作业2

Python求向量的范数
使用对角矩阵对向量的进行缩放

第四章 矩阵分解

一、特征分解

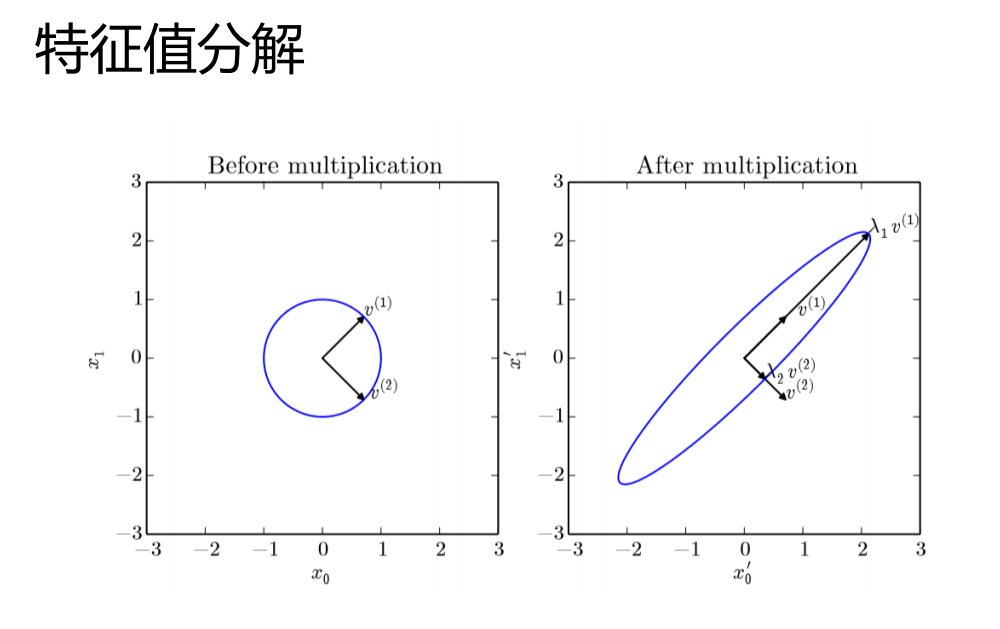
二、奇异值分解

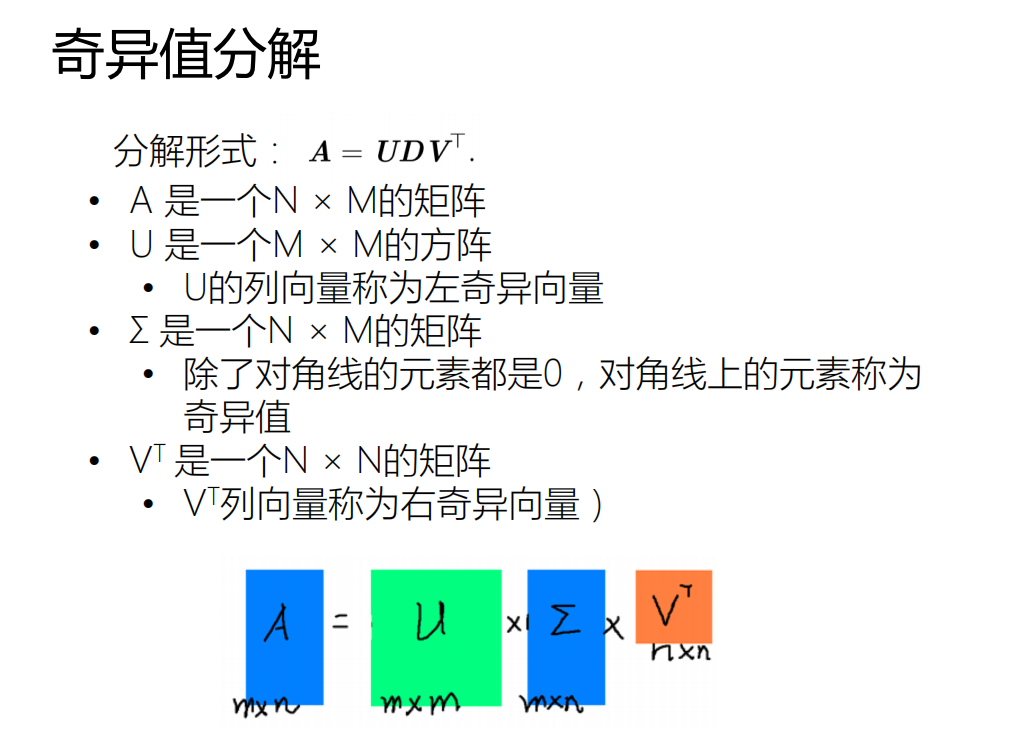
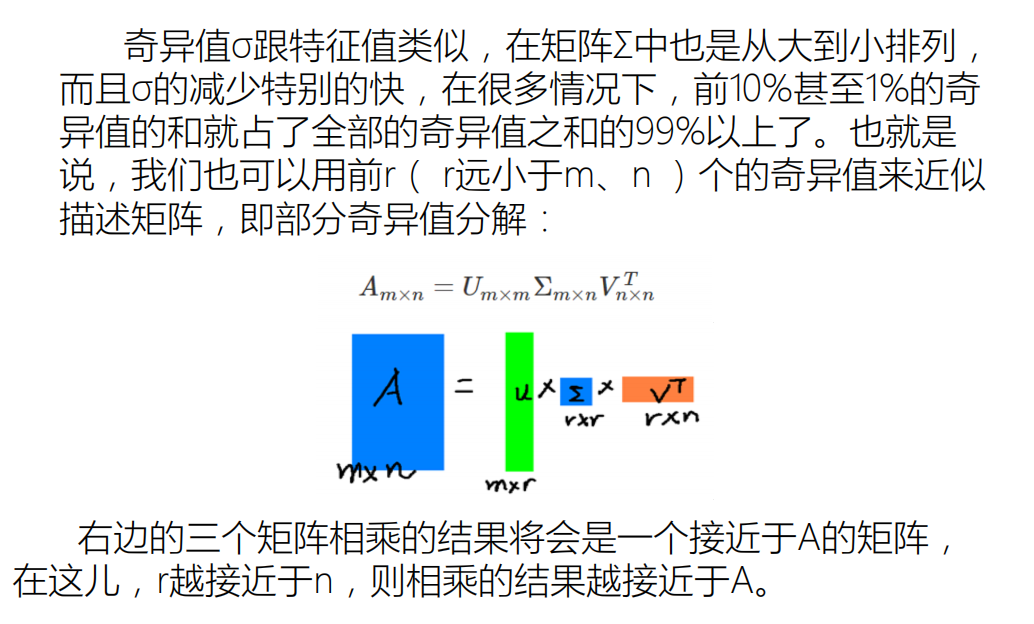
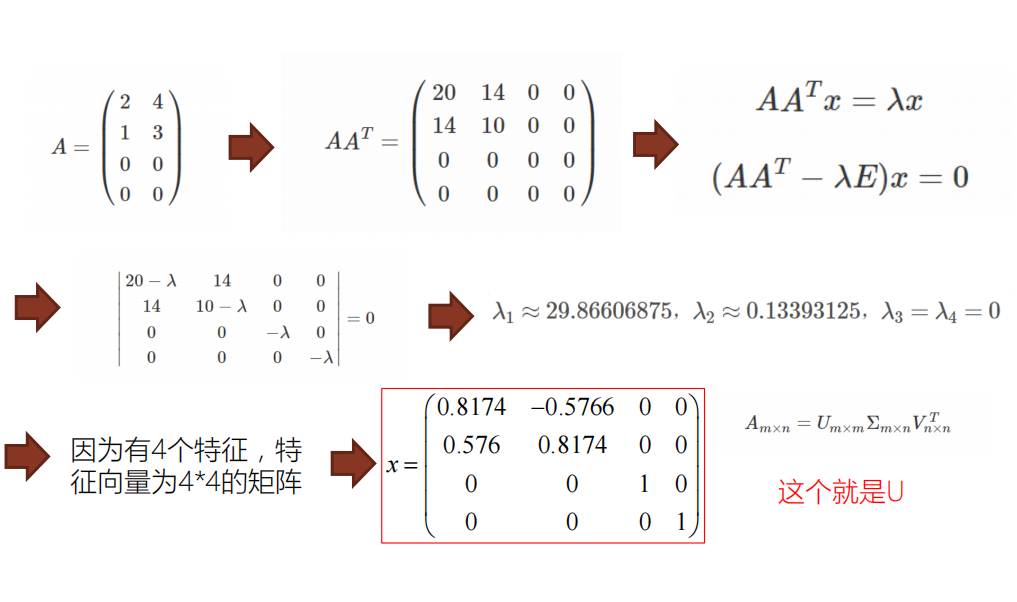
关于SVD一个代码例子

用SVD分解值重新求A的过程，如图

for k in range(k):
  uk = u[:,k].reshape(m,1)
  vk = v[k].reshape(1,n)
  a += sigma[k] * np.dot(uk, vk)

代码解释：
使用2x2矩阵进行举例，容易理解
可以推广到任意shape矩阵。
可以看出，每一次k循环是将一部分的SVD分解内容求出，k越大，叠加的分解内容越多。

作业3

进一步理解SVD代码，用自己的图片测试下分解效果