ML学习笔记- 神经网络
神经网络
有的模型可以有多种算法。而有的算法可能可用于多种模型。在神经网络中,对外部环境提供的模式样本进行学习训练,并能存储这种模式,则称为感知器;对外部环境有适应能力,能自动提取外部环境变化特征,则称为认知器。神经网络在学习中,一般分为有教师和无教师学习两种。感知器采用有教师信号进行学习,而认知器则采用无教师信号学习的。在主要神经网络如Bp网络,Hopfield网络,ART络和Kohonen网络中;Bp网络和Hopfield网络是需要教师信号才能进行学习的;而ART网络和Khonone网络则无需教师信号就可以学习。所谓教师信号,就是在神经网络学习中由外部提供的模式样本信号。
M—P神经元模型
神经元接收来自n个其他神经元传递过来的输入信号,这些输入信号通过带权重的连接进行传递,神经元接收到的总输入值将与阈值进行比较,然后通过激活函数(activation function)处理以产生神经元的输出。
类似生物神经网络的假定特点:
- 每个神经元都是一个多输入单输出的信息处理单元;
- 神经元输入分兴奋性输入和抑制性输入两种类型;
- 神经元具有空间整合特性和阈值特性;
- 神经元输入与输出间有固定的时滞,主要取决于突触延搁
感知机与多层网络
感知机组成:两层神经元
- 输入层:接收外界输入信号传递给输出层
- 输出层:M-P神经单元
- 隐层:输入层与输出层间的一层神经元,拥有激活函数功能
局限
感知机只有一层功能神经元(functional neuron),其学习能力非常有限。感知机只能解决线性可分的问题而无法解决非线性可分问题。
感知机可实现运算
y = f(∑i ωixi - θ)
设激活函数为阶跃函数(x >= 0 取1,x < 0 取0)
- 与
令ω1 = ω2 = 1 , θ = 2
则y = f(x1 + x2 - 2) 当x1 = x2 = 1 时 y =1
- 或
令ω1 = ω2 = 1 , θ = 0.5
则y = f(x1 + x2 - 0.5) 当x1 = 1 或 x2 = 1 时 y = 1。
- 非
令ω1 = -0.6 , ω2 = 0 , θ = -0.5
则y = f(-0.6x + 0.5) 当x1 = 1时 y = 0;
当x1 = 0时 y = 1。
阈值可以当作固定输入为-1的权重
多层前馈神经网络
多层前馈神经网络每层神经元与下一层神经元全互连,神经元之间不存在同层连接,也不存在跨层连接。其中输入层神经元接收外界输入,隐层与输出层神经元对信号进行加工,最终结果由输出层神经元输出。
误差逆传播算法 BP算法
工作流程
原理
实现
1)traingd——梯度下降反向传播
根据梯度下降法更新权值和偏置。
2)newff :前馈网络创建函数
3)train:训练网络
返回训练后的网络和训练记录TR
4)sim:利用网络进行仿真
返回由网络产生的输出。
BP算法训练:监督学习
例一:
clear;
x=-4:0.01:4; %产生[-4,4]之间的行向量
y1=sin((1/2)*pi*x)+sin(pi*x);%期望输出
%step1:newff前馈网络创建函数
%minmax(x)获取输入x的取值范围,min和max,第一个隐藏层其实相当于对输入进行归一化
%第1个隐藏层含1个神经元,激活函数是tansig,第2个隐藏层含15个,激活函数是tansig,输出层含1个,激活函数是线性函数
%训练函数是梯度下降函数traingd
net=newff(minmax(x),[1,15,1],{'tansig','tansig','purelin'},'traingd');
net.trainparam.epochs=6000; %设置最大迭代次数
net.trainparam.goal=0.00001; %设置神经网络训练的目标误差
%step2:训练神经网络,返回训练好的网络和误差记录
net=train(net,x,y1);
%sim:利用网络进行仿真
%step3:获取BP训练后的实际输出
y2=sim(net,x);
%绘图,原图(蓝色光滑线)和仿真效果图(红色+号点线)
plot(x,y1);%画出期望图像
hold on
plot(x,y2,'r+'); %画出训练得到的图像
例二:
clear all
x=[2056 2395 2600 2298 1634 1600 1873 1478 1900 1500 2046 1556]'; m=size(x);
for i=1:m
x(i)=(x(i)-1478)/(2600-1478);
end
a=[0.5152 0.8173 1;0.8173 1 0.7308;1 0.7308 0.1390;0.7308 0.1390 0.1087;0.1390 0.1087 0.3520;0.1087 0.3520 0]';
T=[0.7308 0.1390 0.1087 0.3520 0 0.3761];
net=newff([0 1;0 1;0 1],[5,1],{'tansig','logsig'},'traingd');
net.trainParam.epochs=10000;
net.trainParam.goal=1e-3;
net.trainParam.lr=0.1;
net=train(net,a,T);
Yp=sim(net,a);
scatter(X,T,'fill');
hold on
scatter(X,Yp,'r','fill');
全局最小与局部极小
其他常见神经网络
RBF :分类任务中除BP之外最常用
单隐层前馈神经网络
使用径向基函数作为隐层神经元激活函数
输出层是隐层神经元输出的线性组合
训练:确定神经元中心,常用的方式包括随机残阳、聚类等
利用BP算法等确定参数
ART:"竞争学习"的代表
SOM:最常用的聚类方法之一
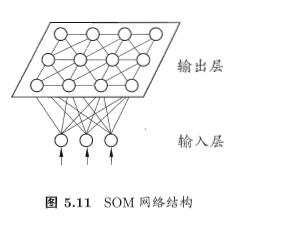
竞争型的无监督神经网络
将高维数据映射到低维空间,高维空间中相似的样本点映射到网络输出层中临近神经元
每个神经元拥有一个权向量
目标:为每个输出层神经元找到合适的权向量以保持拓扑结构
训练
网络接收输入样本后,将会确定输出层的“获胜”神经元(“胜者通吃”)
获胜神经元的权向量将向当前输入样本移动
级联相关网络:“构造性”神经网络的代表
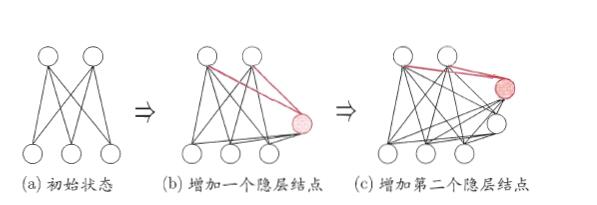
构造性神经网络
将网络的结构也当做学习的目标之一,我往在训练过程中找到适合数据的网络结构
训练
开始时只有输入层和输出层
级联-新的隐层节点逐渐加入,从而创建起层级结构
相关-最大化新节点的输出与网络误差之间的相关性
Elman网络:递归神经网络的代表
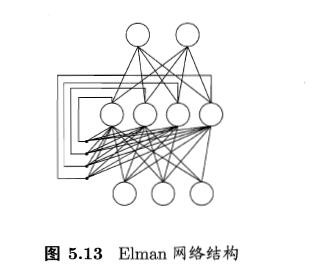
网络可以有环形结构,可让使一些神经元的输出反馈回来最为输入
t 时刻网络的输出状态: 由 t 时刻的输入状态和 t-1时刻的网络状态共同决定
Elman网络是最常用的递归神经网络之一
结构与前馈神经网络很相似,但隐层神经元的输出被反馈回来
使用推广的BP算法训练
Bolyzmann机:"基于能量的模型"的代表
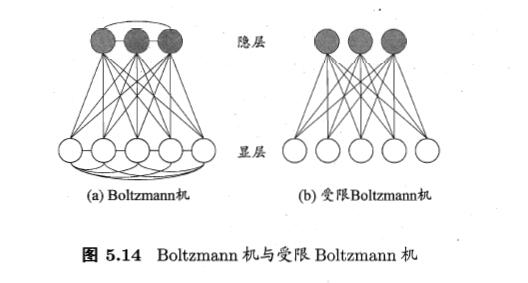
深度学习
深度学习模型就是很深层的神经网络。 无监督逐层训练是多隐层网络训练的有效手段,其基本思想是每次训练一层隐结点,训练时将上一层隐结点的输出作为输入,而本层隐结点的输出作为下一层隐结点的输入,这称为“预训练”;在预训练全部完成后,再对整个网络进行“微调”训练。 另一种节省训练开销的策略是“权共享”,即让一组神经元使用相同的连接权。这个策略在卷积神经网络(简称CNN)中发挥了重要作用。 卷积神经网络用于手写数字识别 可将“深度学习”理解为“特征学习”或“表示学习”:通过多层处理,逐渐将初始的“低层”特征表示转化为“高层”特征表示后,用“简单模型”即可完成复杂的分类等学习任务。
DBN 深度信念网络
DBN 在训练模型的过程中主要分为两步:
第 1 步:分别单独无监督地训练每一层 RBM 网络,确保特征向量映射到不同特征空间时,都尽可能多地保留特征信息;
第 2 步:在 DBN 的最后一层设置 BP 网络,接收 RBM 的输出特征向量作为它的输入特征向量,有监督地训练实体关系分类器.而且每一层 RBM 网络只能确保自身层内的 权值对该层特征向量映射达到最优,并不是对整个 DBN 的特征向量映射达到最优,所以反向传播网络还将错误信息自顶向下传播至每一层 RBM,微调整个 DBN 网络.RBM 网络训练模型的过程可以看作对一个深层 BP 网络权值参数的初始化,使DBN 克服了 BP 网络因随机初始化权值参数而容易陷入局部最优和训练时间长的缺点.这可以很直观的解释,DBNs的BP算法只需要对权值参数空间进行一个局部的搜索,这相比前向神经网络来说,训练是要快的,而且收敛的时间也少。
上述训练模型中第一步在深度学习的术语叫做预训练,第二步叫做微调。最上面有监督学习的那一层,根据具体的应用领域可以换成任何分类器模型,而不必是BP网络。
应用
深度网络是一种良好的无监督学习方法,其特征提取功能能够针对不同概念的粒度大小,能够在很多领域得到广泛的应用。通常,DBN主要用于对一维数据的建模比较有效,例如语音。而通过级联多层卷积网络组成深度网络的模型主要用于二维数据,例如图像等。
卷积神经网络 CNN
它的基本结构由输入层、卷积层(convolu-tional layer )、池化层(pooling layer)也称为下采样层、全连接层及输出层构成。卷积层和池化层一般会取若干个交替设置。由于卷积层中输出特征面的每个神经元与其输入进行局部连接,并通过对应的连接权值与局部输入进行加权求和再加上偏置值,得到该神经元输入值,该过程等同于卷积过程,CNN也由此而得名。
每个卷积层包含多个特征映射,每个特征映射是一个由多个神经元构成的“平面”,通过一种卷积滤波器提取输入的一种特征
采样层亦称“汇合层”,其作用是基于局部相关性原理进行亚采样,从而在减少数据量的同时保留有用信息
连接层就是传统神经网络对隐层与输出层的全连接
寻找极值点的位置
红色为牛顿下降法,绿色为梯度下降法,从图中直观的感觉是,红色线短,下降速度快。因为牛顿下降法是用二次曲面去拟合当前的局部曲面,而梯度下降法是用平面去拟合当前的局部曲面,一般用二次曲面拟合的更好,所以一般牛顿算法收敛快。
梯度下降法
梯度含义
在微积分里面,对多元函数的参数求∂偏导数,把求得的各个参数的偏导数以向量的形式写出来,就是梯度。比如函数f(x,y), 分别对x,y求偏导数,求得的梯度向量就是(∂f/∂x, ∂f/∂y)T,简称grad f(x,y)或者▽f(x,y)。对于在点(x0,y0)的具体梯度向量就是(∂f/∂x0,∂f/∂y0)的转置.或者▽f(x0,y0)
从几何意义上讲,就是函数变化增加最快的地方。具体来说,对于函数f(x,y),在点(x0,y0),沿着梯度向量的方向就是(∂f/∂x0, ∂f/∂y0)T的方向是f(x,y)增加最快的地方。着梯度向量的方向,更加容易找到函数的最大值。沿着梯度向量相反的方向,也就是 -(∂f/∂x0, ∂f/∂y0)T的方向,梯度减少最快,也就是更加容易找到函数的最小值。
实现原理
一阶泰勒展式,其实就是用平面去拟合函数的局部曲面。
f(x+Δx)=f(x)+f′(x)∗Δx
我们的目的是使得左边的值变小,那是不是应该使得下面的式子变为负值。但是如何使得上式一定为负值,简单的方法就是:
Δx=−f′(x)
这样上式就变为
f(x+Δx)=f(x)−f′(x)∗f′(x)
但是不要忘了以上所有的一切只有在局部成立,也就是说在小范围才成立,那么下式就有很能太大
Δx=−f′(x)
所以加个小的修正的因子,上式就变为:
Δx=−μ∗f′(x)
最终得到公式:
xn+1=xn−μ∗f′(xn)
所以梯度下降算法是用平面拟合函数的局部曲面。
实现代码
如:找出f=x^2的极值点
% 设置步长为0.1,f_change为改变前后的y值变化,仅设置了一个退出条件。
syms x;f=x^2;
step=0.1;x=2;k=0; %设置步长,初始值,迭代记录数
f_change=x^2; %初始化差值
f_current=x^2; %计算当前函数值
ezplot(@(x,f)f-x.^2) %画出函数图像
axis([-2,2,-0.2,3]) %固定坐标轴
hold on
while f_change>0.000000001 %设置条件,两次计算的值之差小于某个数,跳出循环
x=x-step*2*x; %-2*x为梯度反方向,step为步长,!最速下降法!
f_change = f_current - x^2; %计算两次函数值之差
f_current = x^2 ; %重新计算当前的函数值
plot(x,f_current,'ro','markersize',7) %标记当前的位置
drawnow;pause(0.2);
k=k+1;
end
hold off
fprintf('在迭代%d次后找到函数最小值为%e,对应的x值为%e\n',k,x^2,x)
牛顿下降法
实现原理
牛顿下降法是用二次曲面去拟合当前的局部曲面,首先考虑一下下式:
f(x+Δx)=f(x)+f′(x)Δx+1/2∗f′′(x)∗Δx2
同样我们希望左式最小,那么将左式看成是△x的函数,当取合适的△x值时,左边的式子达到极小值,此时导数为0。因此对上式进行求导数,得到一下公式:
0=f′(x)+f′′(x)∗Δx
此时可得到公式:
xn+1=xn−f′(xn)/f′′(xn)
所以说牛顿下降法是用二次曲面来拟合函数的局部曲面。
综上而言,牛顿下降法利用了函数的更多的信息,能够更好的拟合局部曲面,所以收敛的速度也会加快。
实现步骤
实现代码
%定义变量
syms x1 x2
f=exp(x1^2-x1+2*x2^2+4);
v=[x1,x2];
%df为f的一阶导数 G为f的二阶导数
df=jacobian(f,v);
df=df.';
G=jacobian(df,v);
%epson:误差
epson=1e-12;
xm=[0,0]';
%将起始点xm(1,1) xm(2,1)的代入x1,x2
g1=subs(df,{x1 x2},{xm(1,1),xm(2,1)});
G1=subs(G,{x1,x2},{xm(1,1),xm(2,1)});
%k:计算迭代的次数
k=0;
while(norm(g1)>epson)%范数
p=-G1\g1;
xm=xm+p;
g1=subs(df,{x1,x2},{xm(1,1),xm(2,1)});
G1=subs(G,{x1,x2},{xm(1,1),xm(2,1)});
k=k+1;
end
k
xm
估算结果---由f函数易看出 当x1=0.5 x2=0时指数上能取到极小值
补充
图像金字塔方法
一幅图像的金字塔是一系列以金字塔形状排列的分辨率逐步降低,且来源于同一张原始图的图像集合。其通过梯次向下采样获得,直到达到某个终止条件才停止采样。我们将一层一层的图像比喻成金字塔,层级越高,则图像越小,分辨率越低。
假设一幅图像的原始像素是n * n,对这幅图像进行下采样就是在原图的基础上每隔一个样本就丢弃一个样本,那么我们就会得到一个像素大小为n/2*n/2的新图。
图像的上采样刚好与上图相反,这个过程直接通过在原图的基础上每一个样本后插入0,从而达到图像尺寸的2倍放大。当然了,直接插入0仅仅是增加了图像的尺寸,同时会引入了噪声。我们通过选择内插函数来代替插入的0。
inputPath ='C:\Users\lenovo\Desktop\photo\';
filename = [inputPath '1.jpg'];
I = im2double(imread(filename));
if size(I,3)==3
I=rgb2gray(I);
end
nlev=4;
sigma=1;
sigma_r=0.1;
f = [.05, .25, .4, .25, .05];
f = f'*f;
%构建拉普拉斯金字塔
pyr = cell(nlev,1);
J = I;
for l = 1:nlev-1
J_gauss = imfilter(J,f,'replicate');
J_gauss_down = J_gauss(1:2:size(J_gauss,1)-1,1:2:size(J_gauss,2)-1); %downsample
J_gauss_high = imresize(J_gauss_down,[size(J_gauss,1) size(J_gauss,2)],'bilinear');
pyr{l} = J-J_gauss_high;
J=J_gauss_down;
end
pyr{nlev}=J_gauss_down;
% for i=1:length(pyr)
% figure;imshow(mat2gray(pyr{i}));
% end
%从金字塔重建图像
out = pyr{nlev};
for l = nlev-1 : -1 : 1
out = pyr{l} + imresize(out,[size(pyr{l},1) size(pyr{l},2)],'bilinear');
end
figure;imshow([mat2gray(out),I]);title('重建之后图像,原图');
syms x 函数
定义一个符号变量: syms x 定义一个符号变量x 后续可以做一些符号操作,如: p=x^2+3*x-2; diff(p,x) %p对x求导

